Chapter 3 Scan Conversion Algorithms Point and Line

Chapter 3 Scan Conversion Algorithms (Point and Line)

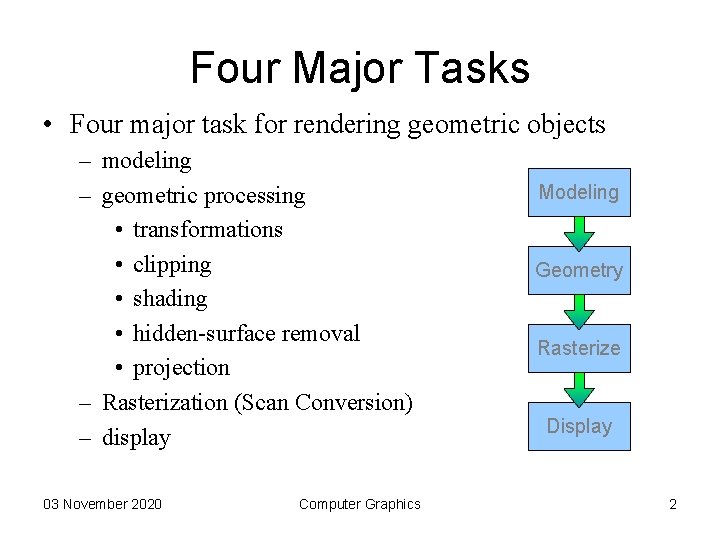
Four Major Tasks • Four major task for rendering geometric objects – modeling – geometric processing • transformations • clipping • shading • hidden-surface removal • projection – Rasterization (Scan Conversion) – display 03 November 2020 Computer Graphics Modeling Geometry Rasterize Display 2

Scan Conversion • Rasterization or Scan Conversion is defined as the process of representing continuous graphic object as a collection of discrete pixels. – Various graphic objects are • • • Point Line Rectangle, Square Circle, Ellipse Sector, Arc Polygons…… – Hardware, Software, Firmware Implementation 03 November 2020 Computer Graphics 3

Scan Conversion • Scan Conversion is required in order to convert vector data to Raster format for a scan line display device – convert each graphic object to a set of regular pixels. – determine inside/outside areas when filling polygons. – scan-convert curves 03 November 2020 Computer Graphics 4

Scan Conversion • The scan conversion process is interleaved with other processes to deliver and improve the final image, some of which are not entirely restricted to the discretization of vectors but are involved in generally determining the colour of each pixel in the raster. e. g: – shading & illumination, – hidden surface removal – texture mapping – depth testing 03 November 2020 Computer Graphics 5

Scan Conversion Algorithms 1. 2. 3. 4. 5. Scan Conversion of Point Scan Conversion of Line Scan Conversion of Circle Scan Conversion of Ellipse Scan Conversion of Polygons 03 November 2020 Computer Graphics 6

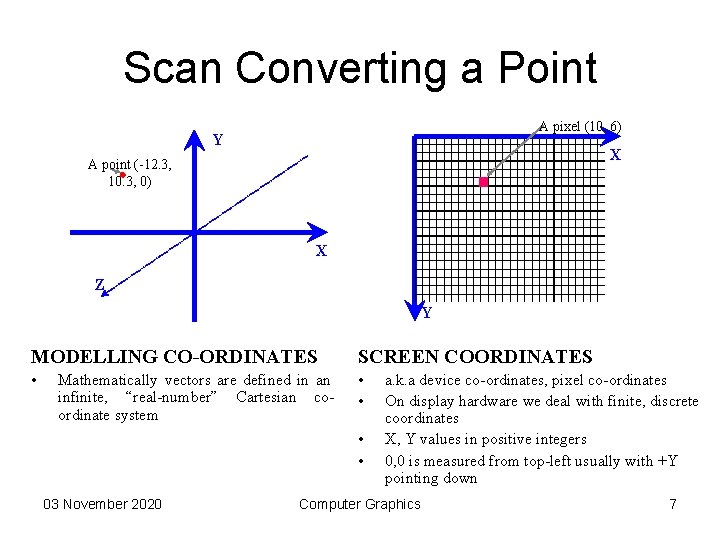
Scan Converting a Point A pixel (10, 6) Y X A point (-12. 3, 10. 3, 0) X Z Y MODELLING CO-ORDINATES SCREEN COORDINATES • • • Mathematically vectors are defined in an infinite, “real-number” Cartesian coordinate system • • 03 November 2020 a. k. a device co-ordinates, pixel co-ordinates On display hardware we deal with finite, discrete coordinates X, Y values in positive integers 0, 0 is measured from top-left usually with +Y pointing down Computer Graphics 7

Scan Converting a Point • Each pixel on graphic display does not represent a mathematical point like P(2. 6, 3. 33). But it can be accommodated to the nearest position by applying few mathematical functions such as – CEIL P (3, 4) – FLOOR P (2, 3) – GREATEST INTEGER FUNCTION P (3, 3) – ROUND P (3, 3) 03 November 2020 Computer Graphics 8

Scan Conversion Algorithms 1. 2. 3. 4. Scan Conversion of Point Scan Conversion of Line Scan Conversion of Circle Scan Conversion of Ellipse 03 November 2020 Computer Graphics 9

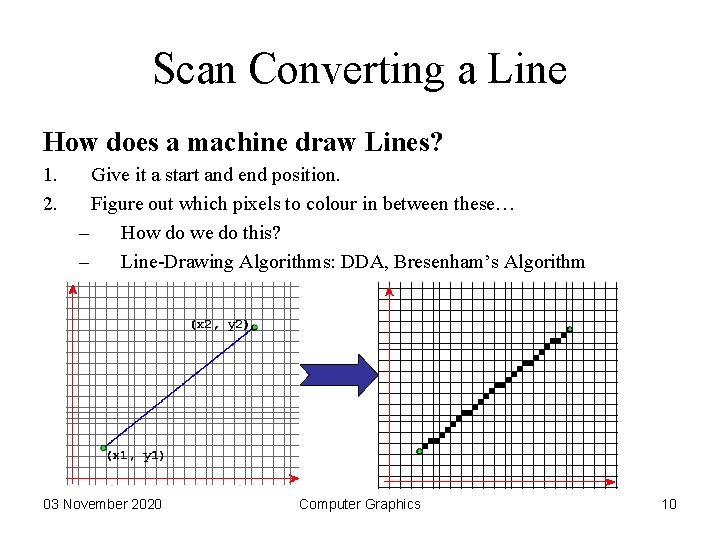
Scan Converting a Line How does a machine draw Lines? 1. 2. Give it a start and end position. Figure out which pixels to colour in between these… – How do we do this? – Line-Drawing Algorithms: DDA, Bresenham’s Algorithm 03 November 2020 Computer Graphics 10

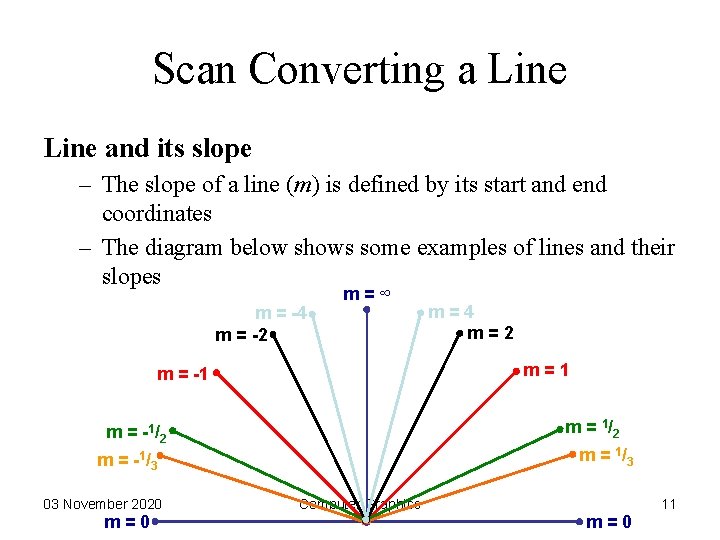
Scan Converting a Line and its slope – The slope of a line (m) is defined by its start and end coordinates – The diagram below shows some examples of lines and their slopes m = -4 m = -2 m=∞ m=1 m = -1 m = 1 /2 m = - 1 /2 m = 1 /3 m = - 1 /3 03 November 2020 m=4 m=2 Computer Graphics m=0 11

Line Drawing Algorithms 1. DDA Line Algorithm 2. Bresenham Line Algorithm 03 November 2020 Computer Graphics 12

DDA Algorithm 1. Introduction – Digital Differential Analyser is an an algorithm for scan-converting lines – The original differential analyzer was a physical machine developed by Vannevar Bush at MIT in the 1930’s in order to solve ordinary differential equations. – It calculates pixel positions along a line by taking unit step increment along one direction and calculating corresponding coordinate position based on the rate of change of the coordinate (Dx or Dy ) (Incremental Approach) 03 November 2020 Computer Graphics 13

DDA Algorithm 2. Basic Concept – For each part of the line the following holds true: – If Dx = 1 i. e. 1 pixel then … – i. e. for each pixel we move right (along the x axis), we need to move down (along the y-axis) by m pixels. – In pixels, the gradient represents how many pixels we step upwards (Dy) for every step to the right (Dx) 03 November 2020 Computer Graphics 14

DDA Algorithm 3. Derivation Assume that 0<m<1, Dx > 0 and Dy >0 For a point P(xi, yi ) on a line we know that yi = mxi + b At next position P(xi+1, yi+1 ) yi+1 = mxi+1+ b Having unit step increment along x-axis means xi+1 = xi + 1 Therefore yi+1 = m(xi + 1)+ b = mxi + m + b = mxi + b + m = yi + m 03 November 2020 Computer Graphics 15

DDA Algorithm 4. Simple Algorithm 1. Input (x 1, y 1) and (x 2, y 2) 2. Let x = x 1; y = y 1; m = (y 2 -y 1)/(x 2 -x 1); 3. Draw pixel (x, y) 4. WHILE (x < x 2) //i. e. we reached the second endpoint 5. { x = x + 1; //step right by one pixel y = y + m; //step down by m pixels Draw pixel (ROUND(x), ROUND(y)); } 03 November 2020 Computer Graphics 16

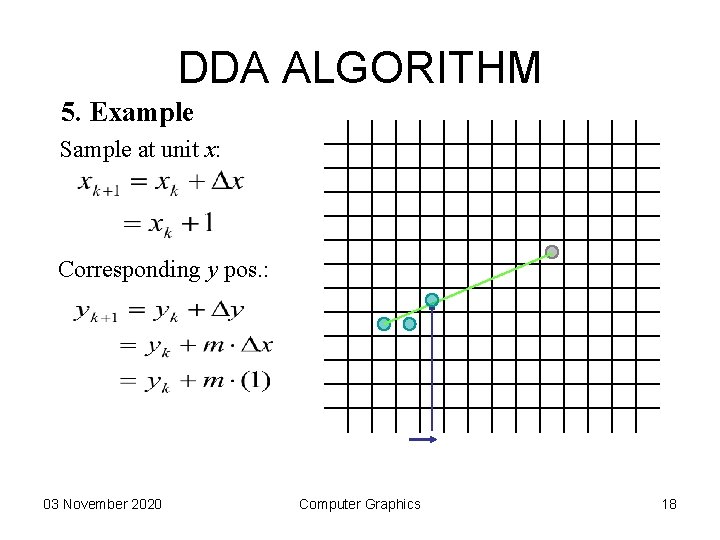
DDA ALGORITHM 5. Example Sample at unit x: Corresponding y pos. : 03 November 2020 Computer Graphics 17

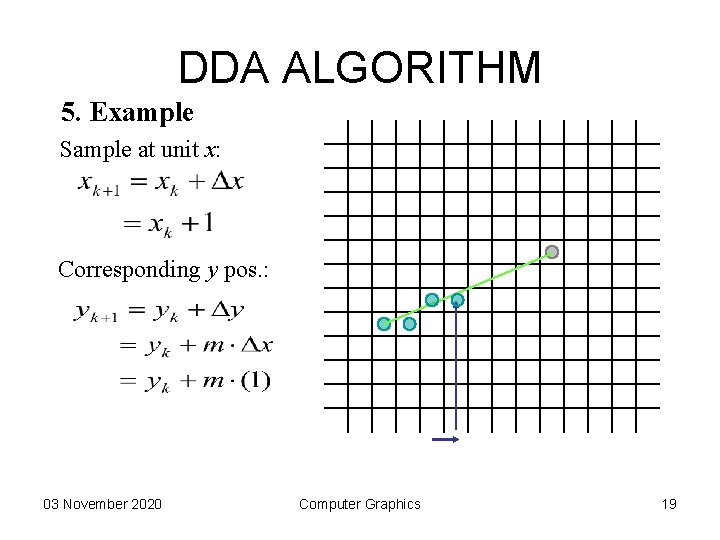
DDA ALGORITHM 5. Example Sample at unit x: Corresponding y pos. : 03 November 2020 Computer Graphics 18

DDA ALGORITHM 5. Example Sample at unit x: Corresponding y pos. : 03 November 2020 Computer Graphics 19

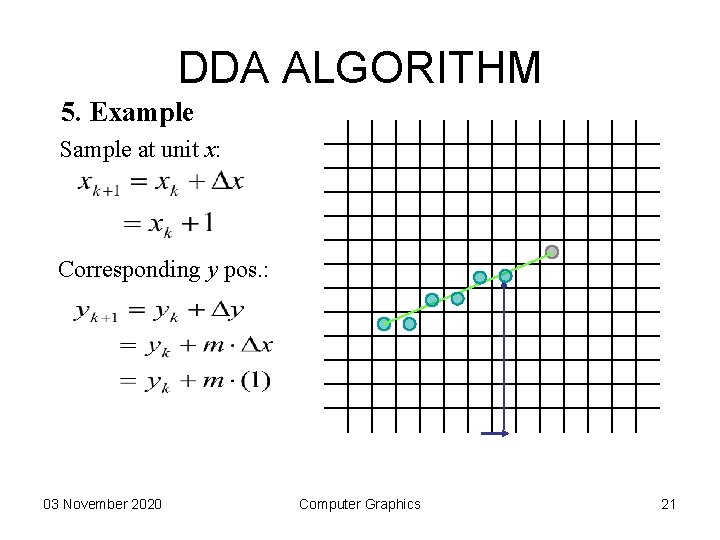
DDA ALGORITHM 5. Example Sample at unit x: Corresponding y pos. : 03 November 2020 Computer Graphics 20

DDA ALGORITHM 5. Example Sample at unit x: Corresponding y pos. : 03 November 2020 Computer Graphics 21

DDA ALGORITHM 5. Example Sample at unit x: Corresponding y pos. : 03 November 2020 Computer Graphics 22

DDA ALGORITHM 5. Example Sample at unit x: Corresponding y pos. : Consider endpoints: P 1(0, 0), P 2(7, 4) 03 November 2020 Computer Graphics 23

DDA ALGORITHM 6. Exercise 1. Consider endpoints: P 1(0, 0), P 2(6, 4) Calculate the points that made up the line P 1 P 2 2. Now, consider endpoints: P 3(0, 0), P 4(4, 6) Calculate the points that made up the line P 3 P 4 What happened with P 3 P 4? ? ? 03 November 2020 Computer Graphics 24

DDA Algorithm 7. Y-Version (|m|>1) – If the slope is very steep (i. e. Dy is much greater than Dx) then there’s a problem. i. e. m is much greater than 1 – This is because we only draw one pixel for each x value (each time we step right) – Solution: if the slope is too big, step for y instead 03 November 2020 Computer Graphics 25

DDA Algorithm 8. Generic solution – Modify Basic idea – Take unit step increment along direction having more rate of change, and compute the coordinates for the other position to maximize the number of points to be computed along the path of line and avoid discontinuities or 03 November 2020 Why? Computer Graphics discontinuity !! 26

DDA Algorithm - Generic solution – What is m<0 ? – We must see the sign of Dx and Dy Various Cases x>0 y>0 x>0 y<0 x<0 y>0 x<0 y<0 |m|<1 xi+1 = xi + 1 yi+1 = yi + m xi+1 = xi + 1 yi+1 = yi - m xi+1 = xi - 1 yi+1 = yi + m xi+1 = xi - 1 yi+1 = yi – m (or swap points) xi+1 = xi + 1/m xi+1 = xi - 1/m yi+1 = yi + 1 yi+1 = yi - 1 yi+1 = yi + 1 xi+1 = xi - 1/m yi+1 = yi – 1 (or swap points) |m|>1 – Or can we have simple solution? ? ? ? 03 November 2020 Computer Graphics 27

DDA Algorithm 1. Input (x 1, y 1) and (x 2, y 2) 2. Compute dx = x 2 -x 1 and dy = y 2 -y 1 m = dx/dy 3. If abs(dx)>abs(dy) step = abs(dx) else step = abs(dy) 4. Compute xinc = dx/step yinc = dy/step 5. Initialize x = x 1 and y = y 1 6. Draw pixel (x, y) 7. For k = 1 to steps do //we reach the other endpoint { x = x + xinc; y = y + yinc; Draw pixel (ROUND(x), ROUND(y)); } 03 November 2020 Computer Graphics 28

DDA Algorithm 8. Limitations – Rounding integers takes time – Variables y and m must be a real or fractional binary because the slope is a fraction – Real variables have limited precision, summing an inexact slope m repetitively introduces a cumulative error buildup 03 November 2020 Computer Graphics 29

DDA Algorithm Rounding Error – Note that the actual pixel position is actually stored as a REAL number (in C/C++/java a float or a double) – But we Round Off to the nearest whole number just before we draw the pixel. X Y 1. 0 0. 33 { 1, 0 } 2. 0 0. 66 { 2, 0 } 3. 0 0. 99 { 3, 1 } 4. 0 1. 32 { 4, 1 } Rounded { x, y } – e. g. if m=. 333 … 03 November 2020 Computer Graphics 30

Line Drawing Algorithms 1. DDA Line Algorithm 2. Bresenham Line Algorithm 03 November 2020 Computer Graphics 31

Bresenham’s Line Algorithm 1. Introduction – One disadvantage of DDA is the ROUNDing part which can be expensive – Developed by Jack Bresenham at IBM in the early 1960 s – One of the earliest algorithms in computer graphics – The Algorithm is based on essentially the same principles but is completely based on integer variables 03 November 2020 Computer Graphics 32

Bresenham’s Line Algorithm 2. Basic Concept – Find the closest integer coordinates to the actual line path using only integer arithmetic – Candidate for the next pixel position Specified Line Path – No division, Efficient comparison, No floating point operations 03 November 2020 Computer Graphics 33

Bresenham’s Line Algorithm 3. Derivation – The algorithm is derived for a line having slope 0< m < 1 in the first quadrant. – Pixel position along the line are plotted by taking unit step increments along the x-direction and determining ycoordinate value of the nearest pixel to the line at each step. – Can be generalized for all the cases 03 November 2020 Computer Graphics 34

Bresenham’s Line Algorithm – Let us assume that P(xk, yk ) is the currently plotted pixel. Q(xk+1, yk+1 ) (xk+1, y ) is the next point along the actual path of line. We need to decide next pixel to be plotted from two candidate positions Q 1(xk+1, yk ) or Q 2(xk+1, yk+1) 03 November 2020 Computer Graphics 35

Bresenham’s Line Algorithm Given the equation of line y = mx + b Thus actual value of y at x = xk+1 is given by y = mxk+1 + b = m(xk + 1) + b Let d 1 = | QQ 1|= distance of yk from actual value of y = y – yk = m(xk + 1) + b – yk d 2 = | QQ 2| = distance of actual value of y from yk +1 = yk+1 – y = (yk + 1)– [m(xk + 1) + b] The difference between these 2 separations is d 1 -d 2 = 2 m(xk + 1) + 2 b –yk– (yk+ 1) = 2 m(xk + 1) – 2 yk + 2 b – 1 03 November 2020 Computer Graphics 36

Bresenham’s Line Algorithm we can define a decision parameter pk for the kth step to by simplifying above equation such that the sign of Pk is the same as the sign of d 1 -d 2, but involves only integer calculations. Define Pk = Δx ( d 1 -d 2) 03 November 2020 Computer Graphics 37

Bresenham’s Line Algorithm If pk< 0 ( d 1 -d 2) <0 distance d 1 is less than d 2 yk is closer to line-path Hence Q 1(xk+1, yk ) is the better choice else Q 2(xk+1, yk+1) is the better choice Thus if the parameter pk is negative lower pixel is plotted else upper pixel is plotted 03 November 2020 Computer Graphics 38

Bresenham’s Line Algorithm To put pk in the iterative form, we derived that 03 November 2020 Computer Graphics 39

Bresenham’s Line Algorithm The first parameter p 0 is directly computed as: p 0 = 2 Δy. x 0 - 2 Δx. y 0 + c = 2 Δy. x 0 - 2 Δx. y 0 + 2 Δy + Δx (2 b-1) Since (x 0, y 0) satisfies the line equation , we also have y 0 = Δy/ Δx * x 0 + b b = y 0 - Δy/ Δx * x 0 Combining the above 2 equations , we will have p 0 = 2Δy – Δx The constants 2Δy, 2Δy – Δx and 2Δy-2Δx are calculated once. 03 November 2020 Computer Graphics 40

Bresenham’s Line Algorithm STEPS FOR BRESENHAM’S LINE DRAWING ALGORITHM (for |m| < 1. 0) 1. 2. 3. 4. 5. Input the two line end-points (x 0, y 0) and (x 1, y 1) Plot the point (x 0, y 0) Compute Δx = x 1 - x 0 , Δy = y 1 - y 0 Initialize p 0 = 2Δy – Δx At each xk along the line, starting at k = 0, perform the following test. If pk < 0 the next point to plot is (xk+1, yk) pk = pk +2Δy else the next point to plot is (xk+1, yk+1) pk = pk +2Δy – 2Δx 6. Repeat step 5 (Δx – 1) times 7. Plot the point (x 1, y 1) 8. Exit 03 November 2020 Computer Graphics 41

03 November 2020 Computer Graphics 42

Bresenham’s Line Algorithm 4. General solution – The algorithm can be generalized for all slopes Cases/ slope |m|<1 |m|>1 Case I x>0 , y>0 Case II x>0, y<0 Case III Case IV x<0, y>0 x<0, y<0 p = 2 dy-dx for x = x 1 to x 2 if p<0 p = p+ 2 dy else { y=y+1 p = p+2(dy-dx)} p = 2 dy-dx for x = x 1 to x 2 if p<0 p = p+ 2 dy else { y=y-1 p = p+2(dy-dx)} swap points Case II Case I p = 2 dx-dy for y= y 1 to y 2 if p<0 p = p+ 2 dx else { x=x+1 p = p+2(dx-dy)} p = 2 dx-dy for y= y 2 to y 1 if p<0 p = p+ 2 dx else { x=x+1 p = p+2(dx-dy)} swap points Case II Case I 03 November 2020 Computer Graphics 43

Bresenham’s Line Algorithm 5. Exercise Calculate pixel positions that made up the line connecting endpoints: (12, 10) and (17, 14). 1. (x 0, y 0) = ? 2. x = ? , y =? , 2 y = ? , 2 y – 2 x =? 3. p 0 = 2 y – x =? k 03 November 2020 pk Computer Graphics (xk+1, yk+1) 44

Bresenham’s Line Algorithm 5. Exercise Calculate pixel positions that made up the line connecting endpoints: (12, 10) and (17, 14). 1. (x 0, y 0) = (12, 10) 2. x = 5, y =4, 2 y = 8, 2 y – 2 x =-2 3. p 0 = 2 y – x =3 k pk 0 3 (xk+1, yk+1) 1 2 03 November 2020 Computer Graphics 45

Bresenham’s Line Algorithm 5. Exercise Calculate pixel positions that made up the line connecting endpoints: (12, 10) and (17, 14). 1. (x 0, y 0) = (12, 10) 2. x = 5, y =4, 2 y = 8, 2 y – 2 x =-2 3. p 0 = 2 y – x =3 03 November 2020 k pk (xk+1, yk+1) 0 3 (13, 11) 1 1 (14, 12) 2 -1 (15, 12) 3 7 (16, 13) 4 5 (17, 14) Computer Graphics 46

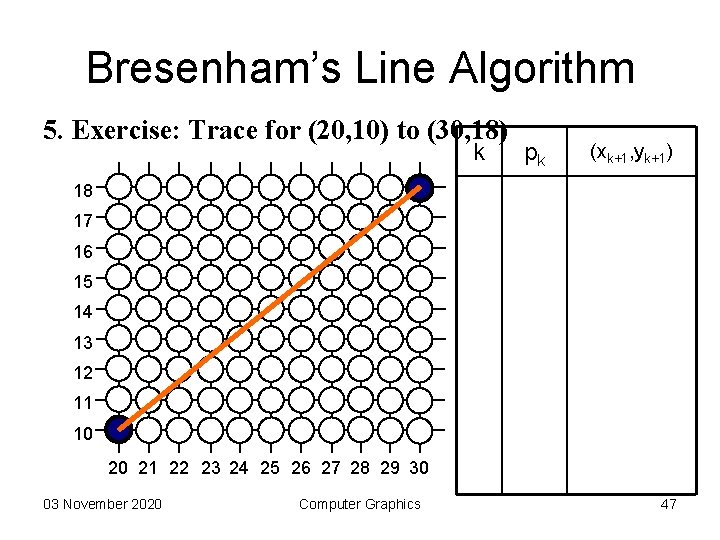
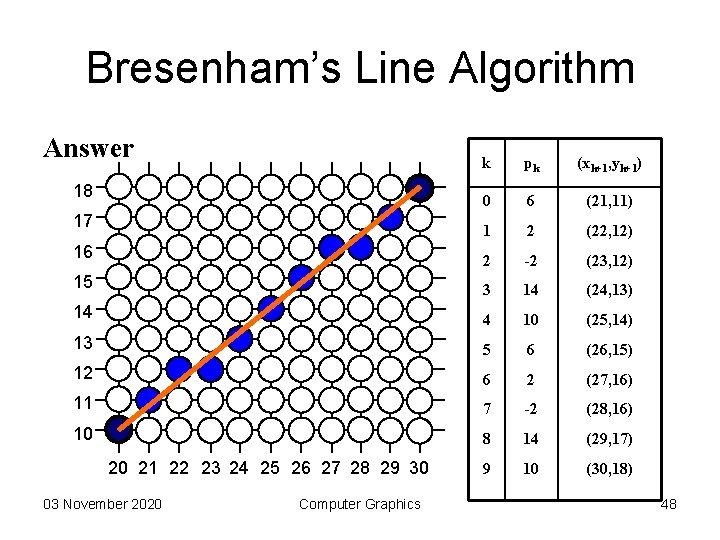
Bresenham’s Line Algorithm 5. Exercise: Trace for (20, 10) to (30, 18) k pk (xk+1, yk+1) 18 17 16 15 14 13 12 11 10 20 21 22 23 24 25 26 27 28 29 30 03 November 2020 Computer Graphics 47

Bresenham’s Line Algorithm Answer k pk (xk+1, yk+1) 0 6 (21, 11) 1 2 (22, 12) 16 2 -2 (23, 12) 15 3 14 (24, 13) 14 4 10 (25, 14) 13 5 6 (26, 15) 12 6 2 (27, 16) 11 7 -2 (28, 16) 10 8 14 (29, 17) 9 10 (30, 18) 18 17 20 21 22 23 24 25 26 27 28 29 30 03 November 2020 Computer Graphics 48