Chapter 3 Regular languages and regular grammars These




















































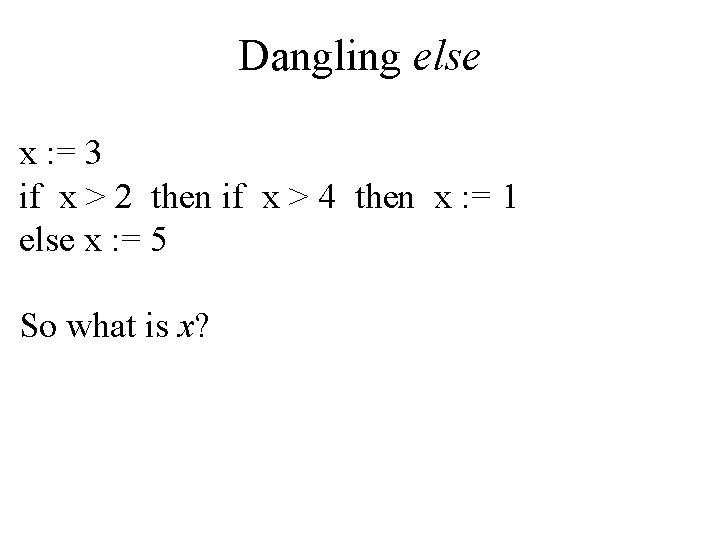














- Slides: 82

Chapter 3 Regular languages and regular grammars These class notes are based on material from our textbook, An Introduction to Formal Languages and Automata, 4 th ed. , by Peter Linz, published by Jones and Bartlett Publishers, Inc. , Sudbury, MA, 2006. They are intended for classroom use only and are not a substitute for reading the textbook.

Operations on formal languages Let L 1 = {10} and L 2 = {011, 11}. Union: L 1 L 2 = {10, 011, 11} Concatenation: L 1 L 2 = {10011, 1011} Kleene Star: L 1* = {λ, 1010, 101010, … } Other operations: intersection, complement, difference

Definition Of Regular Languages A regular language over an alphabet is one that contains either a single string of length 0 or 1, or strings which can be obtained by using the operations of union, concatenation, or Kleene* on strings of length 0 or 1.

Alternative definition of regular languages The simplest possible regular languages are the empty set and languages consisting of a single string that is either the empty string or has length one. For example; if = {a, b}, the simplest languages are , {λ}, {a}, and {b}. A regular language is a language that can be built from these simple languages, by using the three operations of union, concatenation, and Kleene star.

Regular Languages correspond to Regular Expressions • • • L=Ø L = { } L = {a} L = L 1 L 2 L = L 1* RE is Ø RE = a RE = (r 1 + r 2) RE = (r 1*)

Regular expressions A useful shorthand for describing regular languages. Compare to arithmetic expressions, such as (x + 3)/2. An arithmetic expression is constructed using arithmetic operators, such as addition and division. A regular expression is constructed using operations on languages, such as concatenation, union, and Kleene star. The value of an arithmetic expression is a number. The value of a regular expression is a language.

Recursive definition of a regular expression is a regular expression corresponding to the language . λ is a regular expression corresponding to the language {λ}. For each symbol a , a is a regular expression corresponding to the language {a}. For any regular expressions r and s, corresponding to the regular languages L(r) and L(s), respectively, each of the following is a regular expression: (r + s) corresponds to the language L(r) L(s) (r · s) or (rs) corresponds to the language L(r)L(s) (r*) corresponds to the language (L(r))*

Examples a*+ b = {λ, a, b, aaa, aaaaa, … } a*ba* = {w * : w has exactly one b} (a + b)* = any string of a’s and b’s (a + b)*aa (a + b)* = {w * : w contains aa} (a + b)*aa (a + b)* + (a + b)*bb (a + b)* = {w * : w contains aa or bb} (a + λ)b* = {abn : n 0} + {bn : n 0} As with arithmetic expressions, there is an order of precedence for operators -- unless you change it using parentheses. The order is: star closure first, then concatenation, then union.

More examples All strings containing no more than two a’s: (b + c)*(λ + a)(b + c)* All strings containing no runs of a’s of length greater than two: (b + c)*(λ + aa)(b + c)*((b + c)*(λ + aa)(b + c)*)* All strings in which all runs of a’s have lengths that are multiples of three: (aaa + b + c)*

Hints for writing regular expressions Assume = {a, b, c}. Zero or more a’s: a* One or more a’s: aa* Any string at all: (a + b + c)* Any nonempty string: (a + b + c)* Any string that does not contain a: (b + c)* Any string containing exactly one a: (b + c)*a(b + c)*

Practice Let = {a, b, c}. Give a regular expression for the following languages: • all strings containing exactly two a’s • all strings containing no more than three a’s

Practice Let = {a, b, c}. Give a regular expression for the following languages: (a) all strings containing exactly two a’s (b + c)*a(b + c)* ( b) all strings containing no more than three a’s (b + c)*(λ + a)(b + c)*

Practice What languages correspond to the following regular expressions? a*b (aaa + bba) (ab)*

More practice Give regular expressions for the following languages, where the alphabet is = {a, b, c}. -- all strings ending in b -- all strings containing no more than two a’s -- all strings of even length

More practice Give regular expressions for the following languages, where the alphabet is = {0, 1}. -- all strings of one or more 0’s followed by a 1 -- all strings of two or more symbols followed by three or more 0’s -- all strings that do not end with 01

Do these strings match the regular expression? Regular expression String (01* + 1) 0101 (a + λ)b b (ab)*a* λ (a + b)(ab) bb

Accepting (review) Let M = (Q, , q 0, d, A) be an FA. • A string x * is accepted by M if d*(q 0, x) A • The language accepted (or recognized) by M is the set L(M) = {x * | x is accepted by M} • A language L over the alphabet is regular iff there is a Finite Automaton that accepts L.

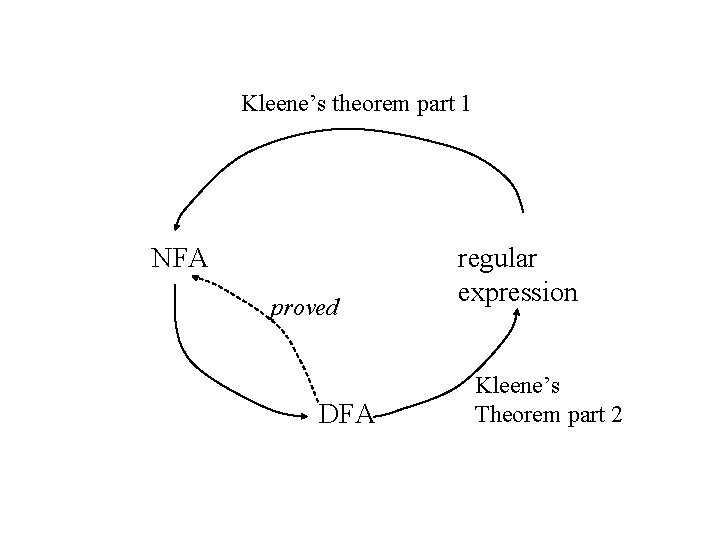
Kleene’s theorem 1) For any regular expression r that represents language L(r), there is a finite automaton that accepts that same language. 2) For any finite automaton M that accepts language L(M), there is a regular expression that represents the same language. Therefore, the class of languages that can be represented by regular expressions is equivalent to the class of languages accepted by finite automata -- the regular languages.

Kleene’s theorem part 1 NFA proved DFA regular expression Kleene’s Theorem part 2

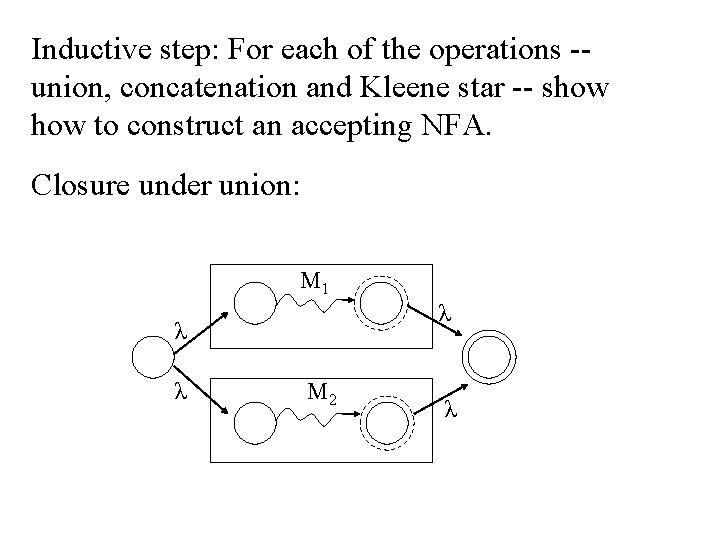
Theorem 3. 1 1 st half of Kleene’s theorem: Let r be a regular expression. Then there exists some nondeterministic regular accepter that accepts L(r). Consequently, L(r) is a regular language. Proof strategy: for any regular expression, we show to construct an equivalent NFA. Because regular expressions are defined recursively, the proof is by induction.

Base step: Give an NFA that accepts each of the simple or “base” languages, , {λ}, and {a} for each a . a

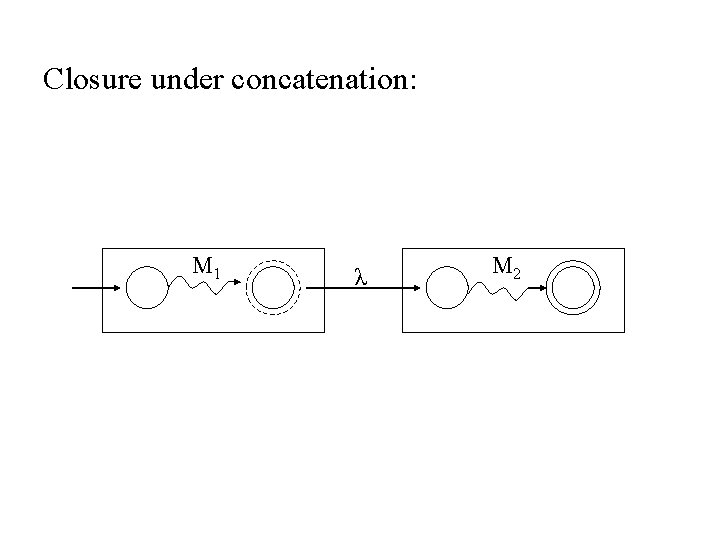
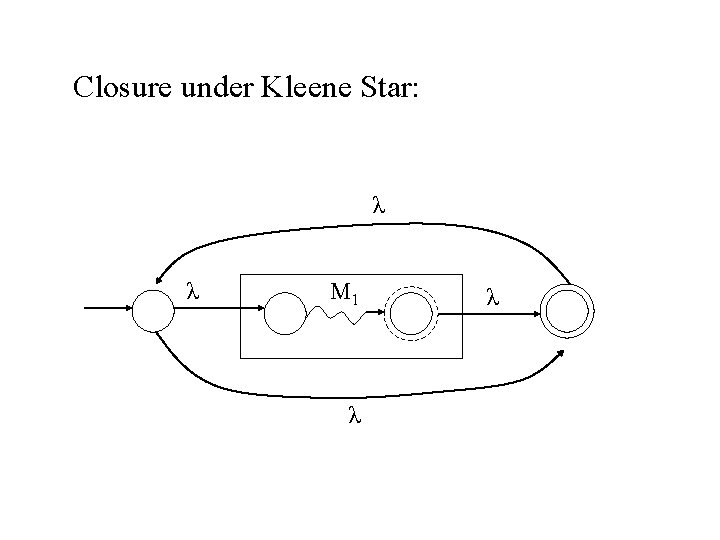
Inductive step: For each of the operations -union, concatenation and Kleene star -- show to construct an accepting NFA. Closure under union: M 1 λ λ λ M 2 λ

Closure under concatenation: M 1 λ M 2

Closure under Kleene Star: λ λ M 1 λ λ

Closure properties of Regular Languages • Union, concatenation, and Kleene star of two regular languages will result in a regular language, since we can write a regular expression for them. • Intersection and difference (complement) of two regular languages will also produce a regular language. • The class of regular languages is said to be closed under these operations. (More in Ch. 4. )

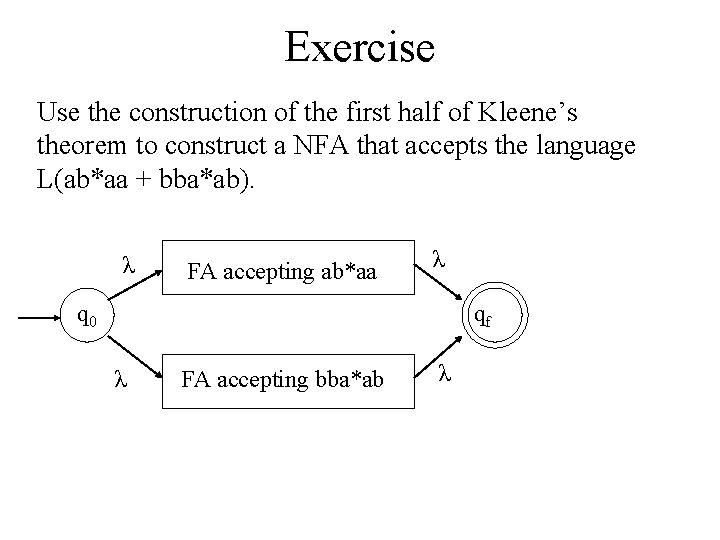
Exercise Use the construction of the first half of Kleene’s theorem to construct a NFA that accepts the language: L(ab*aa + bba*ab).

Exercise Use the construction of the first half of Kleene’s theorem to construct a NFA that accepts the language L(ab*aa + bba*ab). λ FA accepting ab*aa λ q 0 qf λ FA accepting bba*ab λ

Exercise Construct an NFA that accepts the language corresponding to the regular expression: ((b(a+b)*a) + a)

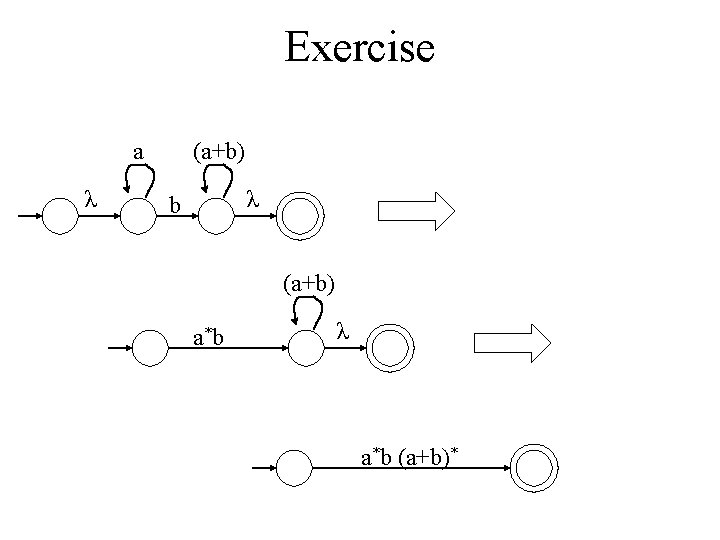
Theorem 3. 2 Kleene’s theorem part 2: Let L be a regular language. Then there exists a regular expression r such that L = L(r). Any language accepted by a finite automaton can be represented by a regular expression. The proof strategy: For any DFA, we show create an equivalent regular expression. In other words, we describe an algorithm for converting any DFA to a regular expression.

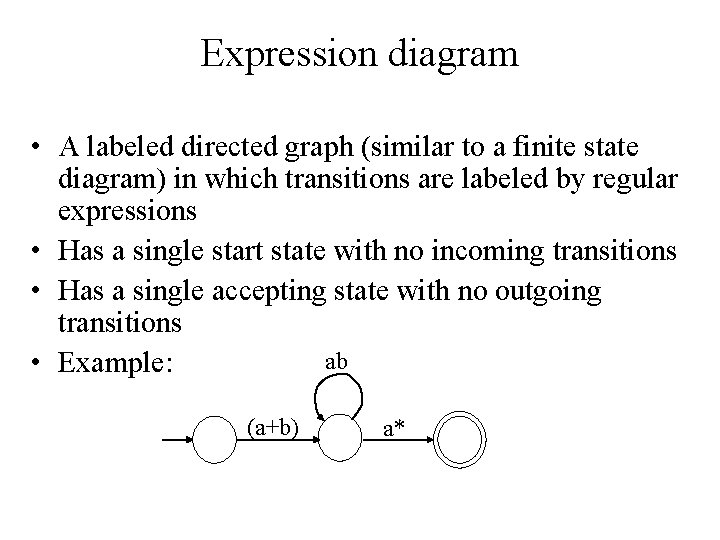
Expression diagram • A labeled directed graph (similar to a finite state diagram) in which transitions are labeled by regular expressions • Has a single start state with no incoming transitions • Has a single accepting state with no outgoing transitions ab • Example: (a+b) a*

Algorithm for converting a DFA into an equivalent regular expression Initial step: Change every transition labeled a, b to (a+b). Add a single start state with an outgoing λ-transition to the current start state, and add a single final state with incoming λ-transitions from every previous final state. Main step: Until expression diagram has only two states (initial state and final state), repeat the following: -- pick some non-start, non-final state -- remove it from the diagram and re-label transitions with regular expressions so that the same language is accepted

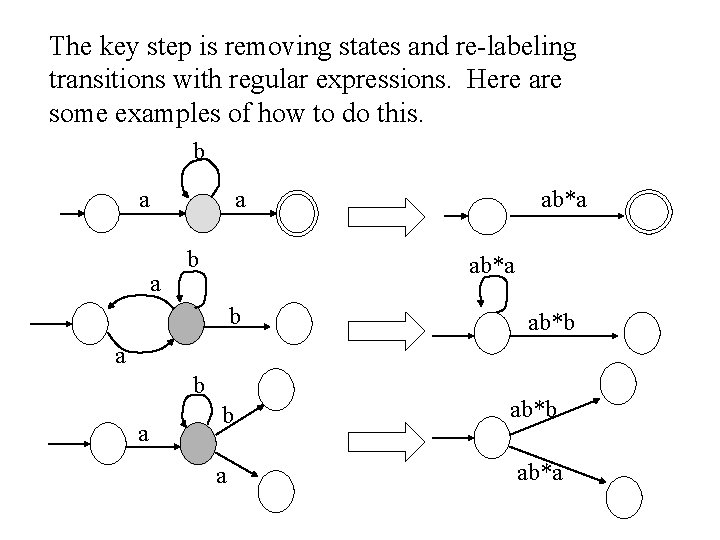
The key step is removing states and re-labeling transitions with regular expressions. Here are some examples of how to do this. b a a a b ab*a b ab*b a ab*a

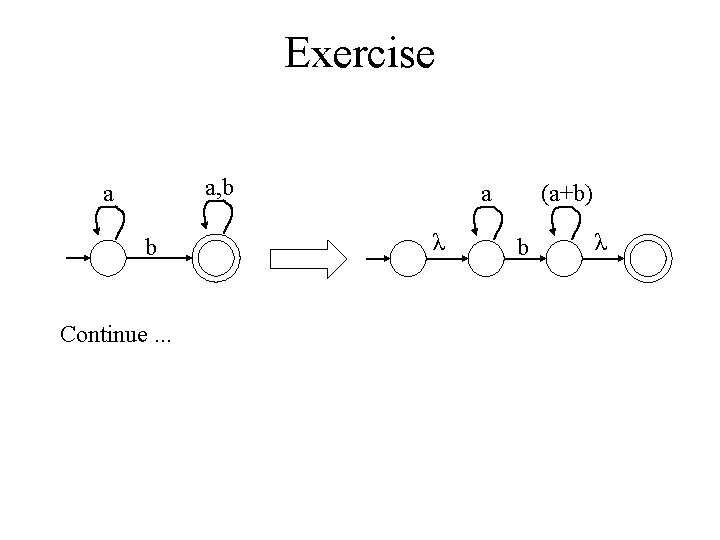
Exercise a, b a b Continue. . . a λ (a+b) b λ

Exercise a λ (a+b) λ b (a+b) a*b λ a*b (a+b)*

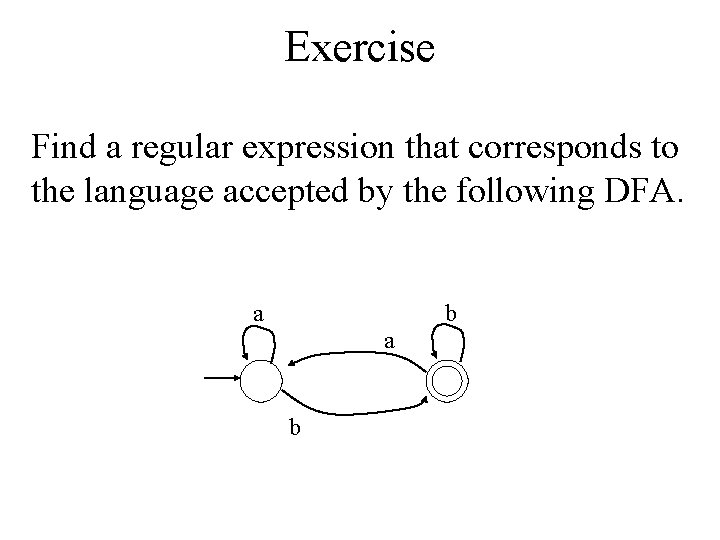
Exercise Find a regular expression that corresponds to the language accepted by the following DFA. a b

Exercise a b a λ λ a*bb*a b a*bb* (a*bb*a)*a*bb* λ

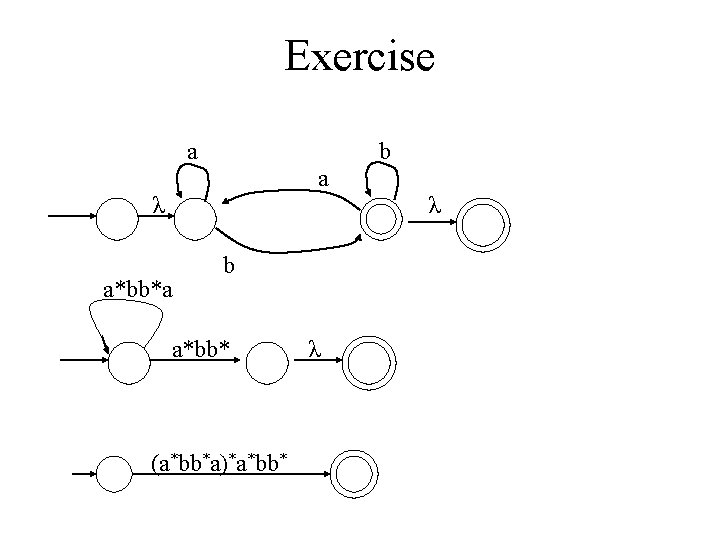
Homework Find a regular expression that corresponds to the language accepted by the following DFA. 0 q 1 q 0 1 0 q 2 0 1 1

Applications of regular expressions • Validation – checking that an input string is in valid format – example 1: checking format of email address on WWW entry form – example 2: UNIX regex command • Search and selection – looking for strings that match a certain pattern – example: UNIX grep command • Tokenization – converting sequence of characters (a string) into sequence of tokens (e. g. , keywords, identifiers) – used in lexical analysis phase of compiler

Grammar • A grammar G = (V, T, S, P) consists of the following quadruple: – a set V of variables (non-terminal symbols), including a starting symbol S NT – a set T of terminals (same as an alphabet, ) – A start symbol S V – a set P of production rules • Example: S a. S | A A b. A | λ

Derivation • Strings are “derived” from a grammar • Example of a derivation S aa. A aab • At each step, a nonterminal is replaced by the sentential form on the right-hand side of a rule (a sentential form can contain nonterminals and/or terminals) • Automata recognize languages; grammars generate languages

Context-free grammar • A grammar is said to be context-free if every rule has a single non-terminal on the left-hand side • This means you can apply the rule in any context. More complicated languages (such as English) have context-dependent rules. A language generated from a context-free grammar is called a context-free language

Regular grammar • A grammar is said to be right-linear if all productions are of the form A x. B or A x, where A and B are variables and x is a string of terminals. (This means that if there is a variable on the right side of the production rule, then it is the rightmost element in the rule. ) • A grammar is said to be left-linear if all productions are of the form A Bx or A x • A regular grammar is either right-linear or leftlinear.

Linear grammar • A grammar can be linear without being right- or left-linear. • A linear grammar is a grammar in which at most one variable can occur on the right side of any production rule, without any restriction on the position of the variable. • Example: S a. S | A A Ab | λ

Another formalism for regular languages • Every regular grammar generates a regular language, and every regular language can be generated by a regular grammar. • A regular grammar is a simpler, specialcase of a context-free grammar • The regular languages are a proper subset of the context-free languages

Exercises • Find a regular grammar that generates the language on = {a, b} consisting of all strings with no more than three a’s.

Exercises • Find a regular grammar that generates the language on = {a, b} consisting of all strings with no more than three a’s S b. S | a. A | λ A b. A | a. B | λ B b. B | a. C | λ C b. C | λ

Exercises • Find a regular grammar that generates the language consisting of even-length strings over {a, b}.

Exercises • Find a regular grammar that generates the language consisting of even-length strings over {a, b}. S aa. S | ab. S | ba. S | bb. S | λ

Non-regular languages • There are non-regular languages that can be generated by context-free grammars • The language {anbn : n 0} is generated by the grammar S a. Sb | λ • The language L = {w : na(w) = nb(w)} is generated by the grammar S SS | λ | a. Sb | b. Sa

Exercise What language is generated by the following context-free (but not regular) grammar? S a. Sa | b. Sb | a | b | λ

Exercise What language is generated by the following context-free grammar? S a. Sa | b. Sb | a | b | λ This is the odd/even palindrome language: L = {w(a+b+λ)w. R}

Programming languages • Programming languages are context-free, but not regular • Programming languages have the following features that require infinite “stack memory” – matching parentheses in algebraic expressions – nested if. . then. . else statements, and nested loops – block structure

Exercise • Given a grammar, you should be able to say what language it generates • Use set notation to define the language generated by the following grammars 1) S aa. SB | λ B b. B | b 2) S a. Sbb | A A c. A | c

Exercise S aa. SB | λ B b. B | b It helps to list some of the strings that can be formed: S aa. SB aab. B aabbbb S aa. SB aaaa. SBB aaaa. Bb aaaabb S aa. SB aaaa. SBB aaaa. Bbb aaaabbb What is the pattern? L = {(aa)nbnb*}

Exercise • Given a language, you should be able give a grammar that generates it. • For example, give a regular (right-linear) grammar for the language consisting of all strings over {a, b, c} that begin with a, contain exactly two b’s, and end with cc.

Exercise • Give a regular (right-linear) grammar for the language consisting of all strings over {a, b, c} that begin with a, contain exactly two b’s, and end with cc: S a. A A b. B | a. A | c. A B b. C | a. B | c. B C a. C | c. D D c

Derivation Given the grammar, S aa. SB | λ B b. B | b the string aab can be derived in two different ways: S aa. SB aab S aa. SB aa. Sb aab

Parse tree Both derivations on the previous slide correspond to the following parse tree. S a a S B e b The tree structure shows the rule that is applied to each nonterminal, without showing the order of rule applications. Each internal node of the tree corresponds to a nonterminal, and the leaves of the derivation tree represent the string of terminals.

Exercise Let G be the grammar S ab. Sc | A A c. Ad | cd 1) Give a derivation of ababccddcc. 2) Build the parse tree for the derivation of that string. 3) Use set notation to define L(G).

Leftmost (rightmost) derivation In a leftmost derivation, the leftmost nonterminal is replaced at each step. In a rightmost derivation, the rightmost nonterminal is replaced at each step. Many derivations are neither leftmost nor rightmost. If there is a single parse tree, there is also a single leftmost derivation.

Ambiguity A grammar is ambiguous if it can generate a string with two possible parse trees. (A string has more than one parse tree if and only if it has more than one leftmost derivation. ) 1. They are looking for teachers of French, German and Japanese. (Are they looking for teachers who can each teach one language or all three languages? ) 2. The lady hit the man with an umbrella. (Is the lady using an umbrella to hit or is she hitting a man who is carrying an umbrella? )

Example Given the following grammar: S S+S|S*S|1|0 The string 1 + 1 * 0 has two different parse trees.

Equivalent grammars Here is a non-ambiguous grammar that generates the same language. S S+A|1|0 A A*B|1|0 B 1|0 Two grammars that generate the same language are said to be equivalent. To make parsing easier, we prefer grammars that are not ambiguous.
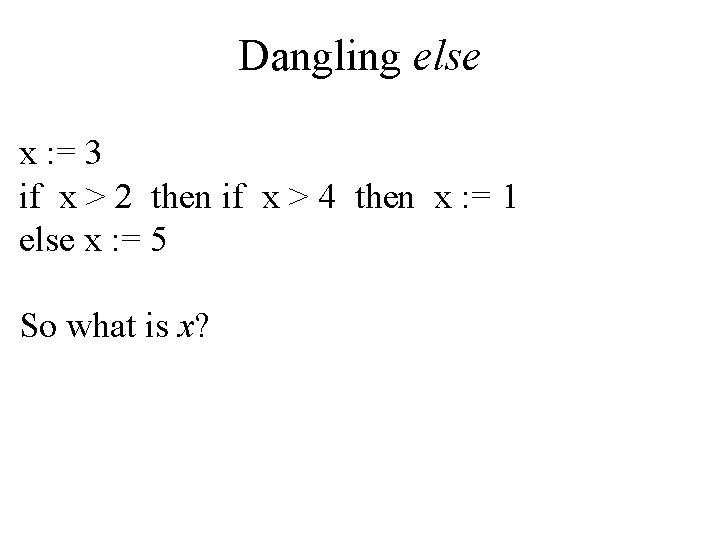
Dangling else x : = 3 if x > 2 then if x > 4 then x : = 1 else x : = 5 So what is x?

Ambiguous vs. unambiguous Ambiguous grammar <statement> : = IF < expression> THEN <statement> | IF <expression> THEN <statement> ELSE <statement> | <otherstatement> Unambiguous grammar <statement> : = <st 1> | <st 2> <st 1> : = IF <expression> THEN <st 1> ELSE <st 1> | <otherstatement> <st 2> : = IF <expression> THEN <statement> | IF <expression> THEN <st 1> ELSE <st 2>

Exercise Show that the following grammar is ambiguous. S AB | aa. B A a | Aa B b Construct an equivalent grammar that is unambiguous.

Parsing • In practical applications, it is usually not enough to decide whether a string belongs to a language. It is also important to know how to derive the string from the language. • Parsing uncovers the syntactical structure of a string, which is represented by a parse tree. (The syntactical structure is important for assigning semantics to the string -- for example, if it is a program).

Parsing Let G be a context-free grammar for C++. Let the string w be a C++ program. One thing a compiler does -- in particular, the part of the compiler called the “parser” -- is determine whether w is a syntactically correct C++ program. It also constructs a parse tree for the program that is used in code generation. There are many sophisticated and efficient algorithms for parsing. You may study them in more advanced classes (for example, on compilers) or come across them on your own. We will not discuss them in this class.

Theorem 3. 3 • Every language generated by a rightlinear grammar is regular. • Proof: – Specify a procedure for automatically constructing an NFA that mimics the derivations of a right-linear grammar.

Theorem 3. 3 • Justification: The sentential forms produced by a right linear grammar have exactly one variable, which occurs as the rightmost symbol. Assume that our grammar has a production rule D d. E and that, during the derivation of a string, there is a step wc. D wcd. E We can construct an NFA which has states D and E, and an arc labeled d from D to E. NFAs can be converted to DFAs. All languages accepted by DFAs are regular.

Theorem 3. 3 Construction: For each variable Vi in the grammar there will be a state in the automaton labeled Vi. The initial state of the automaton will be labeled V 0 and will correspond to the S variable in the grammar. For each production rule Vi a 1 a 2…am. Vj the automaton will have transitions such that δ*(Vi a 1 a 2…am) = Vj For each production rule Vi a 1 a 2…am the automaton will have transitions such that δ*(Vi a 1 a 2…am) = Vfinal

Theorem 3. 3 Construct an NFA that accepts the language generated by the grammar: S a. A convert to: V 0 a. V 1 A ab. S | b V 1 ab. V 0 | b a V 0 b V 1 a b Vf

Theorem 3. 4 • Every regular language can be generated by a right-linear grammar. • Proof: – Generate a DFA for the language. – Specify a procedure for automatically constructing a right-linear grammar from the DFA.

Theorem 3. 4 • Given a regular language L, let M = (Q, , δ, q 0, F) be a DFA that accepts L. Let Q = {q 0, q 1, …, qn} and = {a 1, a 2, …, am}. • Construct the grammar G = (V, T, S, P) with: V = {q 0, q 1, …, qn} T = {a 1, a 2, …, am} S = q 0. P = {} initially. • P, the set of production rules, is constructed as follows:

Theorem 3. 4 • For each transition δ(qi, aj) = qk in the transition table of M, add to P the production: qi ajqk • If qk is in F, then add to P the production: qk λ

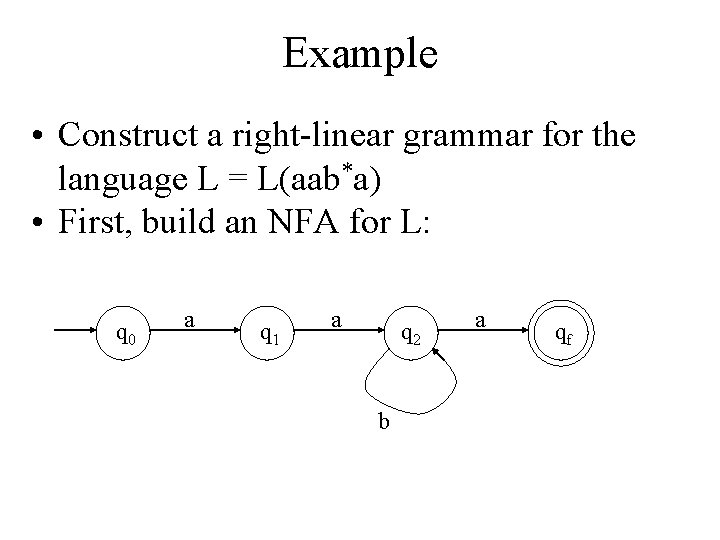
Example • Construct a right-linear grammar for the language L = L(aab*a) • First, build an NFA for L: q 0 a q 1 a q 2 b a qf

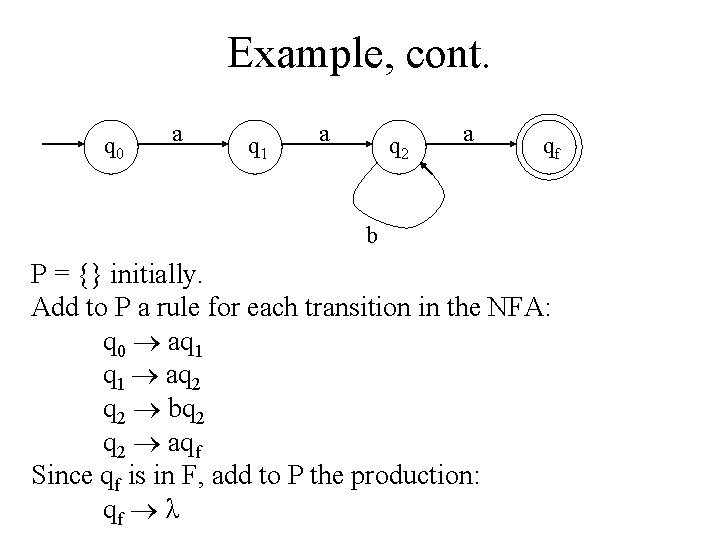
Example, cont. q 0 a q 1 a q 2 a qf b P = {} initially. Add to P a rule for each transition in the NFA: q 0 aq 1 aq 2 bq 2 aqf Since qf is in F, add to P the production: qf λ

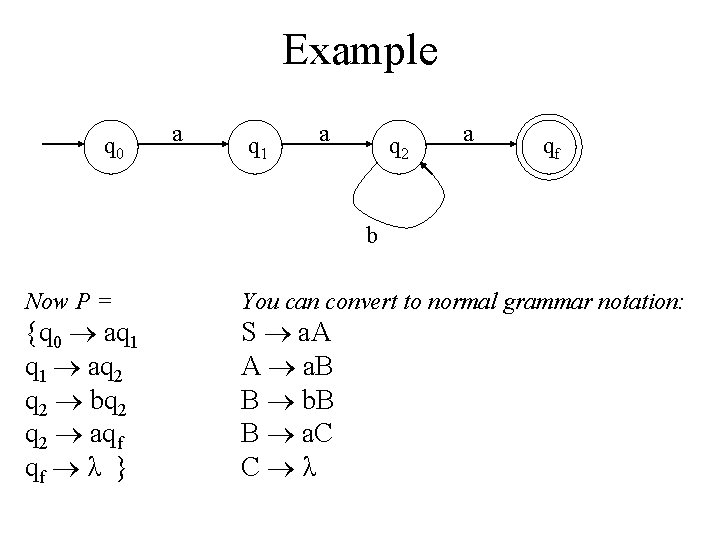
Example q 0 a q 1 a q 2 a qf b Now P = {q 0 aq 1 aq 2 bq 2 aqf qf λ } You can convert to normal grammar notation: S a. A A a. B B b. B B a. C C λ

Theorem 3. 5 A language L is regular if and only if there exists a left-linear grammar G such that L = L(G). Proof: The strategy here is a little tricky. We describe an algorithm to construct a rightlinear grammar that generates the reverse of all the strings generated by the left-linear grammar.

Theorem 3. 5 Given any left-linear grammar we can construct from it an right-linear grammar G’ by replacing productions of the form: A Bv with A v. RB and A v with A v. R Since L(G’) is generated by a right-linear grammar, it is regular. It can be demonstrated that L(G) = (L(G’))R. It can be proven that the reverse of any regular language is also regular (see exercise 12, section 2. 3 in the Linz text). Hence, L is regular.

Theorem 3. 6 A language L is regular if and only if there exists a regular grammar G such that L = L(G). Proof: Combine our definition of regular grammars, which includes the statement, “A regular grammar is either right-linear or left-linear”, with theorems 3. 4 and 3. 5

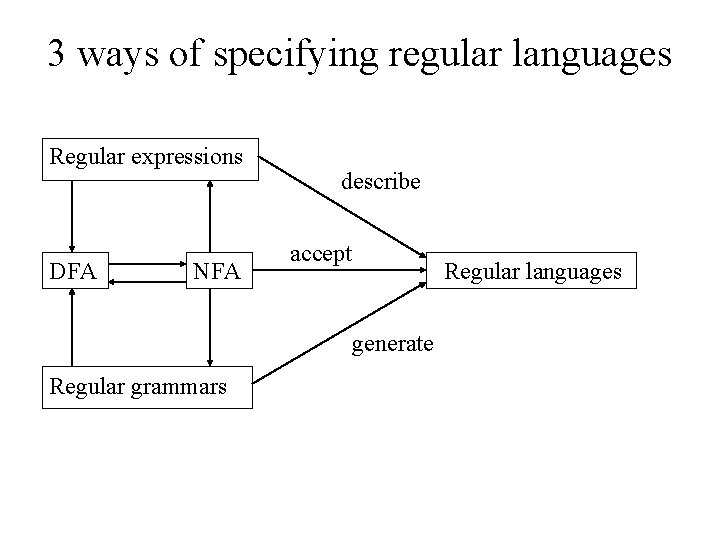
3 ways of specifying regular languages Regular expressions DFA NFA describe accept Regular languages generate Regular grammars
 Regular grammar generates regular language
Regular grammar generates regular language Unrestricted grammar
Unrestricted grammar Questions on context free grammar
Questions on context free grammar Removal of epsilon productions
Removal of epsilon productions Chomsky hierarchy of grammars
Chomsky hierarchy of grammars Regular and irregular languages
Regular and irregular languages Pumping lemma non regular languages examples
Pumping lemma non regular languages examples Decision properties of regular languages
Decision properties of regular languages Decision properties of regular language
Decision properties of regular language Closure properties of regular languages
Closure properties of regular languages Decision properties of regular languages
Decision properties of regular languages Decision properties of regular languages
Decision properties of regular languages Properties of regular languages
Properties of regular languages Contradict example
Contradict example Right linear grammar to left linear grammar
Right linear grammar to left linear grammar Real-time systems and programming languages
Real-time systems and programming languages Cs 421 programming languages and compilers
Cs 421 programming languages and compilers Modern languages for life and work
Modern languages for life and work Aural language in media
Aural language in media Difference between front end and back end languages
Difference between front end and back end languages European master in lexicography
European master in lexicography Defence centre for languages and culture
Defence centre for languages and culture Difference between strongly and weakly typed languages
Difference between strongly and weakly typed languages List the primitives that specify a data mining task.
List the primitives that specify a data mining task. Performance task for media and information literacy
Performance task for media and information literacy Formal languages and automata theory tutorial
Formal languages and automata theory tutorial Automata theory tutorial
Automata theory tutorial Formal languages and automata theory tutorial
Formal languages and automata theory tutorial Advantages and disadvantages of programming languages
Advantages and disadvantages of programming languages Gtg stands for in automata
Gtg stands for in automata Sound devices and figures of speech
Sound devices and figures of speech Csci 3130
Csci 3130 Automata theory tutorial
Automata theory tutorial Real time programming language
Real time programming language Decision properties of context free languages
Decision properties of context free languages Closure property of cfl
Closure property of cfl Translators and facilities of languages
Translators and facilities of languages School of languages cultures and societies
School of languages cultures and societies Cs 421 uiuc
Cs 421 uiuc Data mining languages and system architecture
Data mining languages and system architecture Cross-lingual name tagging and linking for 282 languages
Cross-lingual name tagging and linking for 282 languages Why do languages vary among places
Why do languages vary among places Assembly language list
Assembly language list Jumlah level dalam gambar ini adalah . . . .
Jumlah level dalam gambar ini adalah . . . . Turing unrecognizable languages
Turing unrecognizable languages 5 love languages results
5 love languages results Love language test results
Love language test results Love language test for teens
Love language test for teens Types of love language
Types of love language 11 official languages of south africa
11 official languages of south africa How many languages are there
How many languages are there What is ruby
What is ruby Roman achievements that are still used today
Roman achievements that are still used today Relational query languages in dbms
Relational query languages in dbms Introduction to scripting languages
Introduction to scripting languages Real time example of multithreading in java
Real time example of multithreading in java Languages
Languages New zealand national sport
New zealand national sport Flexive languages
Flexive languages Carol can speak three foreign languages
Carol can speak three foreign languages Love language list
Love language list Low-level programming language
Low-level programming language Asian languages written
Asian languages written Four love languages
Four love languages Programming languages levels
Programming languages levels Introduction to programming languages
Introduction to programming languages Sino-tibetan languages
Sino-tibetan languages Decidable languages
Decidable languages History of computer languages
History of computer languages Plc coding language
Plc coding language Minority definition
Minority definition Euphemism etymology
Euphemism etymology Australian defence force school of languages
Australian defence force school of languages A collection of interrelated data files or tables
A collection of interrelated data files or tables Dbms languages
Dbms languages Database languages
Database languages Category 1 languages
Category 1 languages Pumping lemma for cfl
Pumping lemma for cfl Uga romance languages
Uga romance languages Language
Language What languages come from latin
What languages come from latin Joey paquet
Joey paquet Imperative programming languages
Imperative programming languages









































































































