CHAPTER 3 Real Numbers and the Coordinate Plane

CHAPTER 3 Real Numbers and the Coordinate Plane

3 -1 EXPLORING SQUARE ROOTS AND IRRATIONAL NUMBERS Objectives: To simplify the square root of a perfect square. To estimate without a calculator the square root of a number. (non perfect square)

VOCAB Perfect Square: a number made by squaring a whole number. http: //www. mathsisfun. com/definitions/perfect-square. html Square Root: The square root of a number is a value that, when multiplied by itself, gives the number. https: //www. mathsisfun. com/definitions/square-root. html Irrational Number: a real number that cannot be written as a simple fraction http: //www. mathsisfun. com/irrational-numbers. html Real Numbers: Positive or negative, large or small, whole numbers or decimal numbers are all Real Numbers.

A PERFECT SQUARE Multiply a number times itself to get a perfect square: 1 x 1=1 1 is a perfect square 2 x 2=4 4 is a perfect square 3 x 3=9 9 is a perfect square

YOU TRY… Write the perfect squares up to 225 (15 x 15)

ANSWERS 4 x 4 = 16 5 x 5 = 25 6 x 6 = 36 7 x 7 = 49 8 x 8 = 64 9 x 9 = 81 10 x 10 = 100 11 x 11 = 121 12 x 12 = 144 13 x 13 = 169 14 x 14 = 196 15 x 15 = 225

SQUARE ROOTS

YOU TRY…

ESTIMATING SQUARE ROOTS (WHEN ITS NOT PERFECT)

LETS TRY ANOTHER ONE!

YOU TRY!

PRACTICE Complete pages 109 – 110 #’s 9 -21, 32 -34, 36, 38 -47

3 -2 THE PYTHAGOREAN THEOREM Objective: To use the Pythagorean theorem to determine the length of the hypotenuse of a right triangle given the lengths of the legs.

VOCAB: Legs: Sides of the right triangle opposite the acute angles. Hypotenuse: Longest side of the triangle, opposite the right angle. Pythagorean theorem: a 2 + b 2 = c 2 (leg) 2 + (leg) 2 = (Hypotenuse) 2

EXAMPLE 1 Leg 1 = 3 Leg 2 = 4 Hypotenuse = x ? 3 32 + 4 2 = x 2 9 + 16 = x 2 25 = 5=x x 2 4

EXAMPLE 2 Find the missing side (the hypotenuse) 242 + 122 = x 2 24 x 576 + 144 = x 2 720 = x 2 26. 8 = x 12
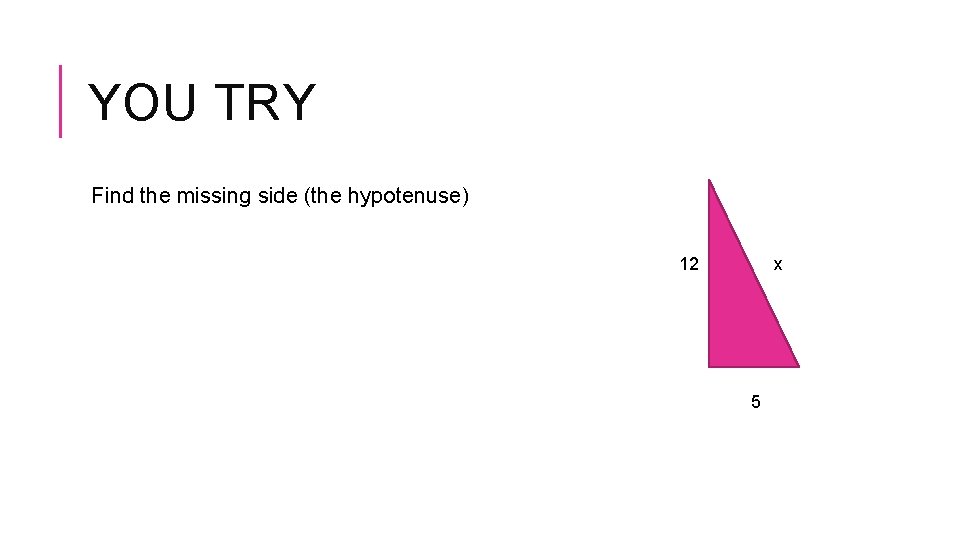
YOU TRY Find the missing side (the hypotenuse) 12 x 5

PRACTICE Page 114 – 115 #’s 1 – 20, 23

3 -3 USING THE PYTHAGOREAN THEOREM Objective: To use the Pythagorean theorem to determine the length of a leg of a right triangle given the lengths of a leg and the hypotenuse.

NOTE* You should use the same formula to start. (leg) 2 + (leg) 2 = (Hypotenuse) 2 Make sure you are putting the hypotenuse in the correct spot!!!

EXAMPLE 1 x 2 + 62 = 102 x 2 + 36 = 100 - 36 -36 x 10 x 2 = 64 x=8 6
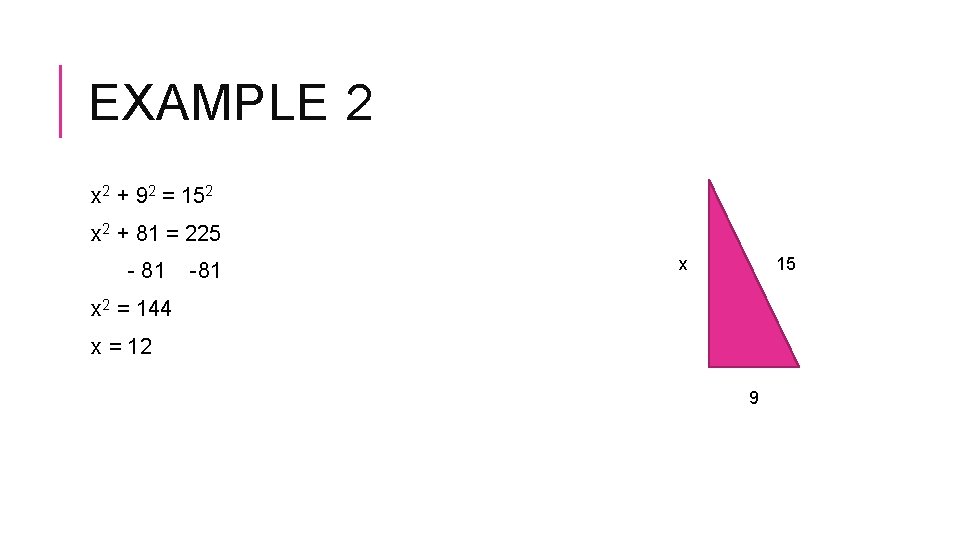
EXAMPLE 2 x 2 + 92 = 152 x 2 + 81 = 225 - 81 -81 x 15 x 2 = 144 x = 12 9
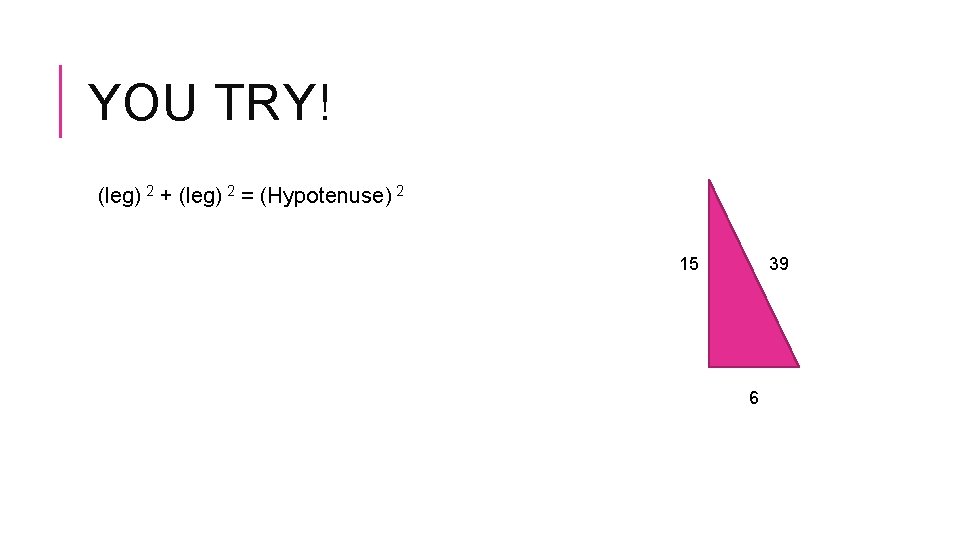
YOU TRY! (leg) 2 + (leg) 2 = (Hypotenuse) 2 15 39 6

PRACTICE Page 120 – 121 #’s 1 - 19

3 -4 GRAPHING IN THE COORDINATE PLANE Objective: To graph points and use the Pythagorean theorem to determine the distance between two points.

VOCAB: Coordinate Plane: a grid formed by the intersection of two number lines. Y – Axis: vertical number line. X – Axis: horizontal number line. Quadrants: the axes divide the plane into 4 sections called quadrants. Origin: the point where the number lines intersect, (0, 0). Ordered Pairs: (x, y) gives the coordinates of the location of a point. X-Coordinate: the first number tells the horizontal units from the origin. Y-Coordinate: the second number tells the vertical units from the origin.
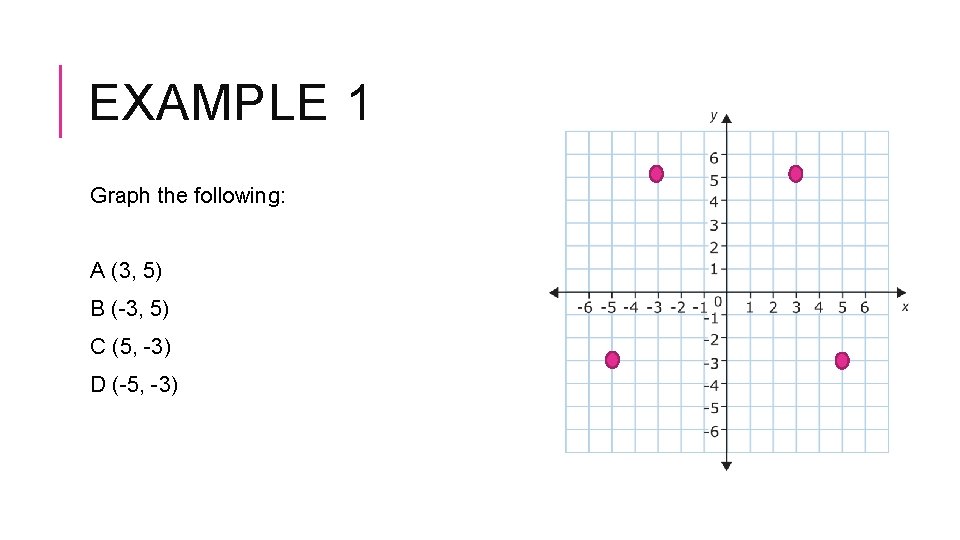
EXAMPLE 1 Graph the following: A (3, 5) B (-3, 5) C (5, -3) D (-5, -3)
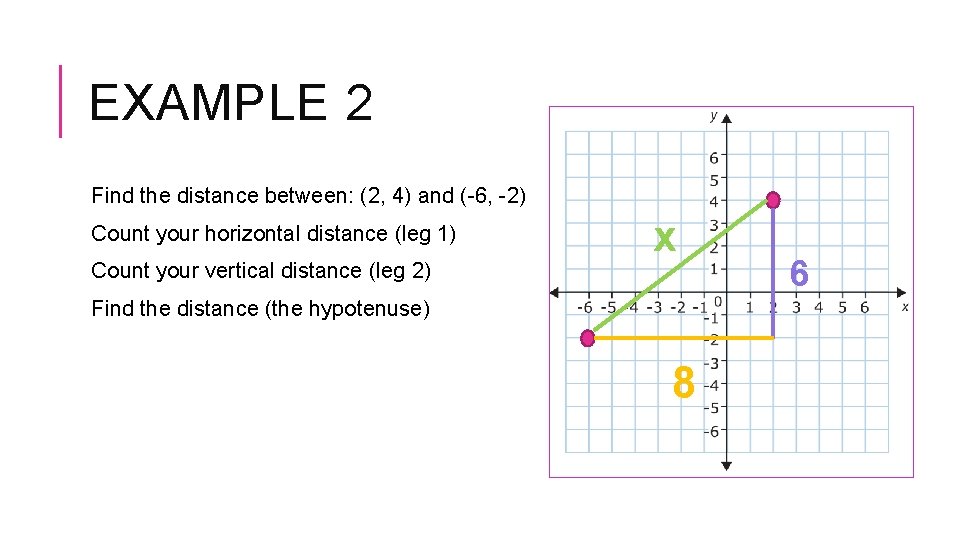
EXAMPLE 2 Find the distance between: (2, 4) and (-6, -2) Count your horizontal distance (leg 1) Count your vertical distance (leg 2) x Find the distance (the hypotenuse) 8 6
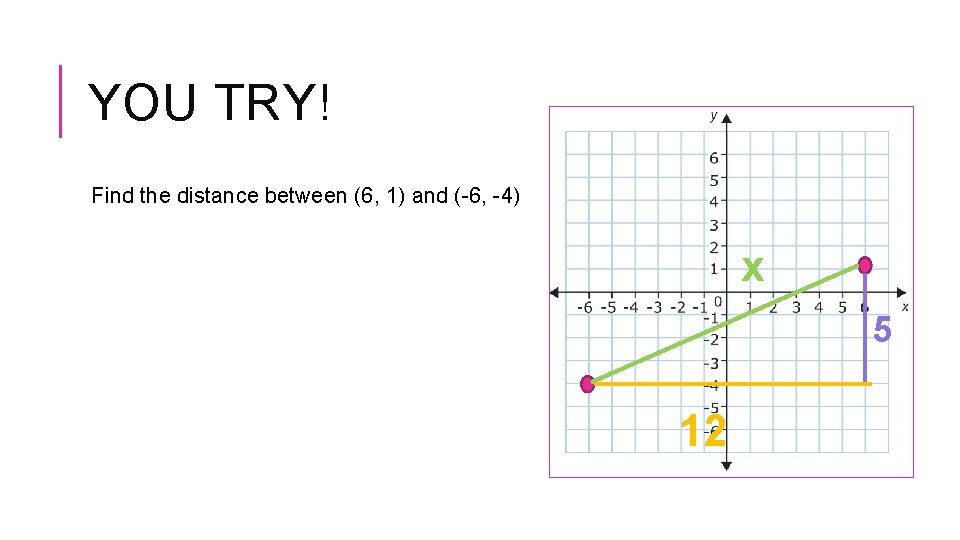
YOU TRY! Find the distance between (6, 1) and (-6, -4) x 5 12

PRACTICE Page 126 #’s 1 – 25

3 -5 EQUATIONS, TABLES AND GRAPHS Objectives: To create a table (chart) given an equation To create a graph given a chart or an equation

VOCAB Solution: a number or pair of numbers that creates a correct answer. Linear Equation: a set of points that forms a line.

NOTES Goal: to have y = mx + b Step 1: add/subtract “x” term Step 2: divide by the number with the ‘y” term Step 3: create a chart Step 4: graph the points from the chart
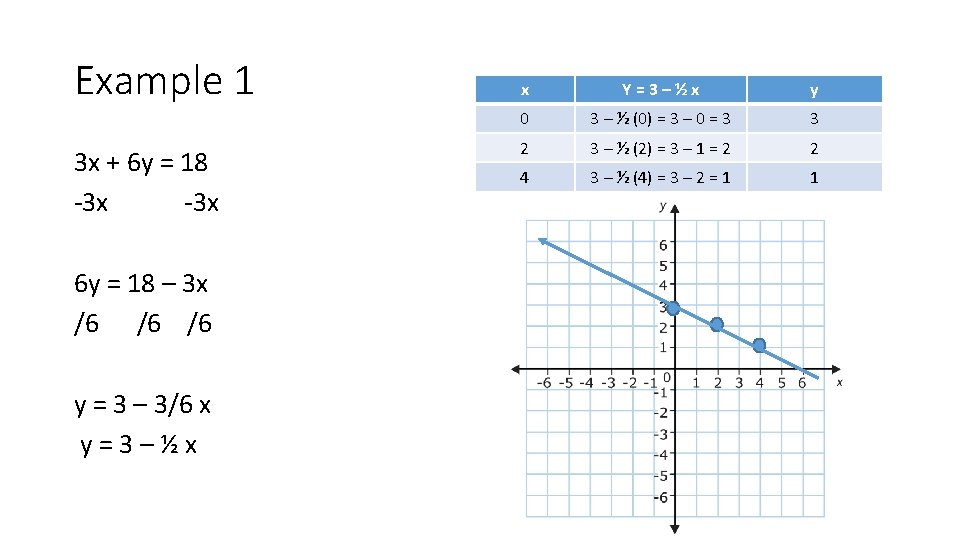
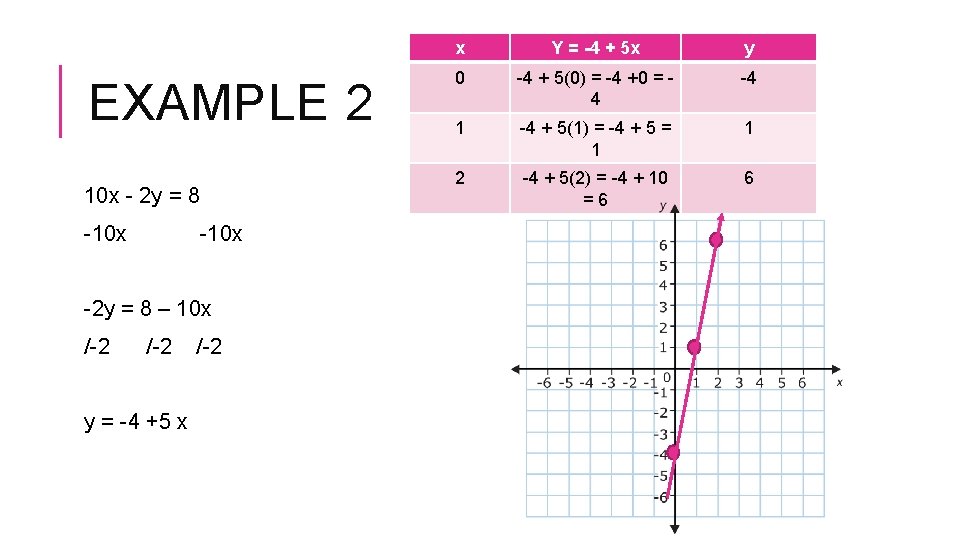
EXAMPLE 2 10 x - 2 y = 8 -10 x -2 y = 8 – 10 x /-2 y = -4 +5 x /-2 x Y = -4 + 5 x y 0 -4 + 5(0) = -4 +0 = 4 -4 1 -4 + 5(1) = -4 + 5 = 1 1 2 -4 + 5(2) = -4 + 10 =6 6

YOU TRY Graph -4 x + 2 y = 6

PRACTICE page 132 #’s 1 -4, 10 -12 worksheet

3 -6 TRANSLATION Objective: To translate a figure a given amount horizontally and vertically. To determine the amount a figure was translated.
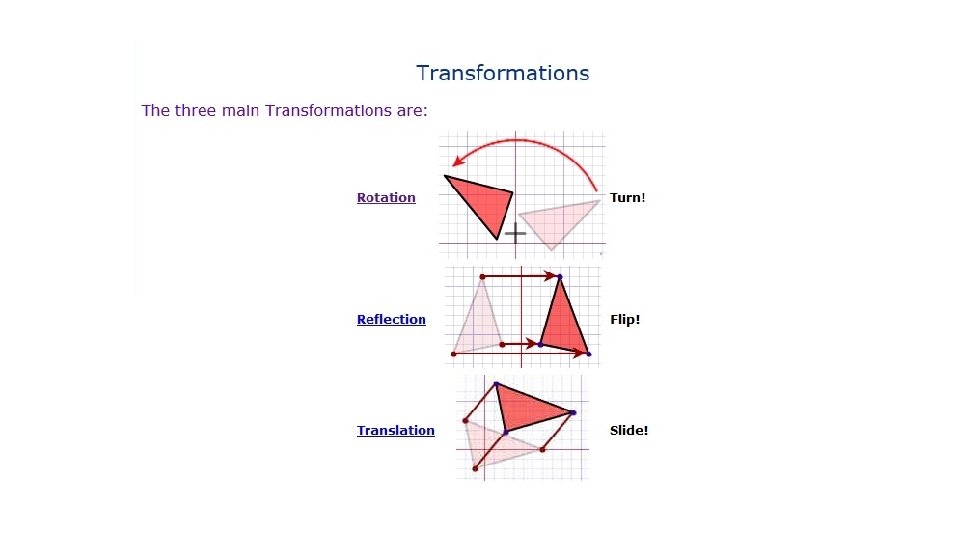

NOTES Link: https: //www. youtube. com/watch? v=Xdj. H_EWh. CZ 0

PRACTICE Page 137 – 139 #’s 1 - 18

3 -7 REFLECTIONS Objectives: To graph the reflection of an object in a coordinate plane. To determine the line of reflection given the original and final object positions.

VOCAB Reflection: a flip Line of Reflection: the line that the figure is flipped over.

EXAMPLE 1 https: //www. youtube. com/watch? v=j 1 X_UIOv. Ew. A

PRACTICE Page 143 -144 #’s 1 – 16, 22 - 25

3 -7 SYMMETRY Objective: to identify if a shape has reflectional symmetry or rotational symmetry. Vocab: Reflectional symmetry is when a shape can be reflected onto itself. Lines of Symmetry: the line that divides the shape into two pieces that are reflections of each other.

EXAMPLE https: //www. youtube. com/watch? v=PBW 1 dy. Ow. Ub. A

PRACTICE Page 143 – 144 #’s 17 - 21
- Slides: 48