Chapter 3 Quadratic Functions Section 3 1 Introduction

Chapter 3 Quadratic Functions Section 3. 1 Introduction to Quadratic Functions Section 3. 2 Quadratic Expressions Section 3. 3 Converting to Factored and Vertex Form Section 3. 4 Quadratic Equations Section 3. 5 Factoring Hidden Quadratics Section 3. 6 Complex Numbers ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 1 Introduction to Quadratic Functions Section 3. 1 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 1 Let ℎ(t) be the height of the ball thrown. Show that Figure 3. 1 is shaped like the graph of h(t) = − 16 t 2 + 32 t + 128, t ≥ 0. Solution Figure 3. 1: Height of a ball thrown from the top of a building Table 3. 1 shows values of ℎ, which fit the points marked in Figure 3. 1. The rises from 128 ft when t = 0 to a height of 144 ft when t = 1, returns to 128 ft when t = 2, and reaches the ground height 0 ft, when t = 4. Table 3. 1 Height of a ball t (seconds) h(t) (ft. ) 0 1 2 3 4 128 144 128 80 0 Figure 3. 1 shows that quadratic functions have graphs that bend, and this shape is consistent with the values in Table 3. 1. Section 3. 1 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 2 In Example 1, the height ℎ(t), in feet of the ball t seconds after it is thrown off the top of a building is given by h(t) = − 16 t 2 + 32 t + 128. (a) What is the practical meaning of the value 128? How can you see this value in the graph of the function in Figure 3. 1? (b) What effect does the sign of the coefficient − 16 have on the graph of the function? Solution (a) The constant term 128 gives the height of the ball when t = 0. This means the top of the building (where the ball is at time t = 0) is 128 feet above the ground. We see this since Figure 3. 1 has a vertical intercept at 128. (b) Because the coefficient − 16 is negative, the term − 16 t 2 counteracts the positive terms 32 t and 128. As a result of the negative coefficient − 16, the graph in Figure 3. 1 goes up at first, reaches a maximum height, and then goes down as the ball falls back to the ground. Section 3. 1 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Interpreting Quadratic Functions Expressed in Standard Form A quadratic function in x is one that can be written in standard form y = f(x) = ax 2 + bx + c, a, b, c constants, a ≠ 0. • The term ax 2 is called the quadratic term or leading term, and its coefficient a is the leading coefficient. · If a > 0, the graph of f is a parabola that opens upward. · If a < 0, the graph of f is a parabola that opens downward. • The term bx is called the linear term. • The term c is called the constant term. It is the vertical intercept of the graph of f. The shape of the graph of a quadratic function is called a parabola. In Example 2, the coefficient of the quadratic term is negative, and as a result the parabola opens downward. If the coefficient of the quadratic term is positive then the parabola opens upward. Section 3. 1 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

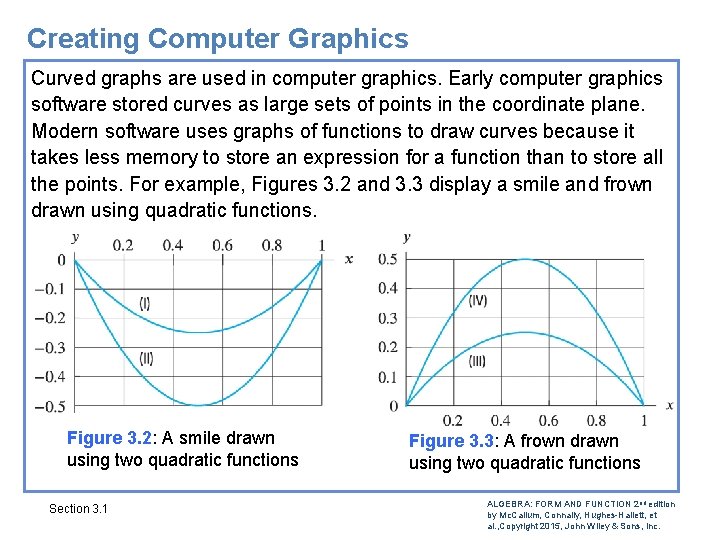
Creating Computer Graphics Curved graphs are used in computer graphics. Early computer graphics software stored curves as large sets of points in the coordinate plane. Modern software uses graphs of functions to draw curves because it takes less memory to store an expression for a function than to store all the points. For example, Figures 3. 2 and 3. 3 display a smile and frown drawn using quadratic functions. Figure 3. 2: A smile drawn using two quadratic functions Section 3. 1 Figure 3. 3: A frown drawn using two quadratic functions ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Interpreting Quadratic Functions to Fit Graphics Example 3 a (a) Write the quadratic function in standard form and identify the coefficients a, b, and c. (i) f(x) = 2 x(x − 1) (ii) g(x) = x(x − 1) Solution (a) (i) Distributing 2 x, we have f(x) = 2 x(x − 1) = 2 x 2 − 2 x, which is in standard form with a = 2, b = − 2, and c = 0. (ii) Distributing x, we have g(x) = x(x − 1) = x 2 − x, which is in standard form with a = 1, b = − 1, and c = 0. Section 3. 1 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

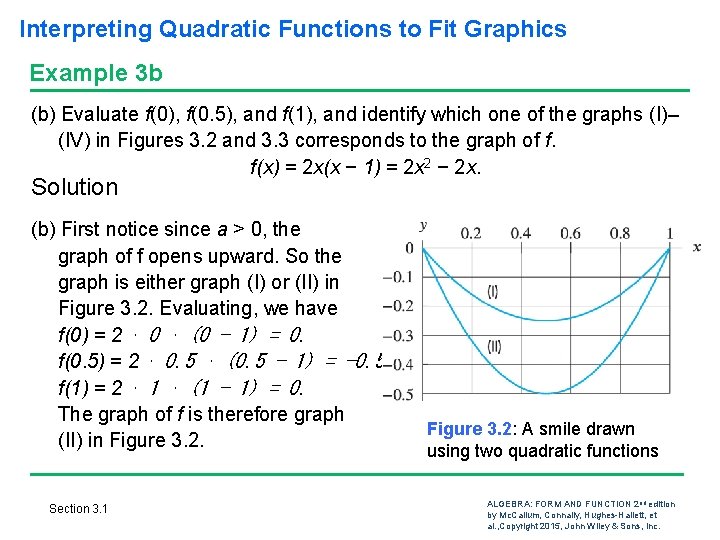
Interpreting Quadratic Functions to Fit Graphics Example 3 b (b) Evaluate f(0), f(0. 5), and f(1), and identify which one of the graphs (I)– (IV) in Figures 3. 2 and 3. 3 corresponds to the graph of f. f(x) = 2 x(x − 1) = 2 x 2 − 2 x. Solution (b) First notice since a > 0, the graph of f opens upward. So the graph is either graph (I) or (II) in Figure 3. 2. Evaluating, we have f(0) = 2 ⋅ 0 ⋅ (0 − 1) = 0. f(0. 5) = 2 ⋅ 0. 5 ⋅ (0. 5 − 1) = − 0. 5. f(1) = 2 ⋅ 1 ⋅ (1 − 1) = 0. The graph of f is therefore graph (II) in Figure 3. 2. Section 3. 1 Figure 3. 2: A smile drawn using two quadratic functions ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

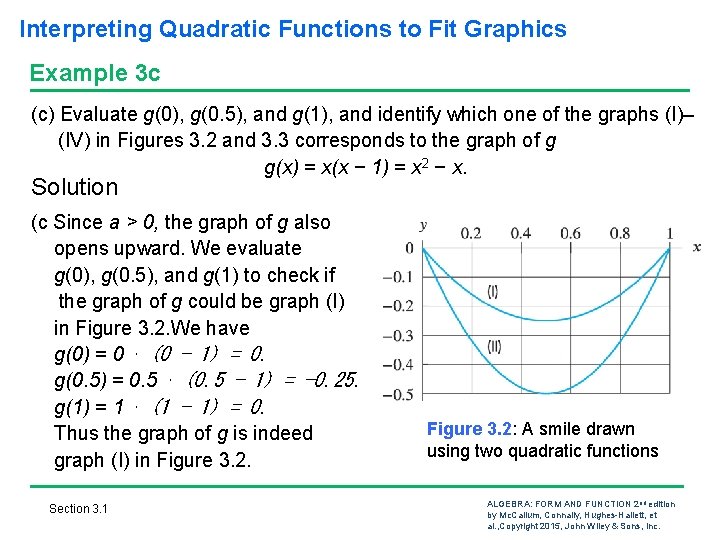
Interpreting Quadratic Functions to Fit Graphics Example 3 c (c) Evaluate g(0), g(0. 5), and g(1), and identify which one of the graphs (I)– (IV) in Figures 3. 2 and 3. 3 corresponds to the graph of g g(x) = x(x − 1) = x 2 − x. Solution (c Since a > 0, the graph of g also opens upward. We evaluate g(0), g(0. 5), and g(1) to check if the graph of g could be graph (I) in Figure 3. 2. We have g(0) = 0 ⋅ (0 − 1) = 0. g(0. 5) = 0. 5 ⋅ (0. 5 − 1) = − 0. 25. = 1 ⋅ (1 − 1) = 0. g(1) Thus the graph of g is indeed graph (I) in Figure 3. 2. Section 3. 1 Figure 3. 2: A smile drawn using two quadratic functions ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 1 QUADRATIC FUNCTIONS Key Points • The standard form shows the vertical intercept • Curves in computer graphics • Expressing quadratic functions in different forms reveals different properties of the function Section 3. 1 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 2 Quadratic Expressions Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Interpreting Quadratic Functions Expressed in Factored Form Example 1 The function h(t) = − 16 t 2 + 32 t + 128 in Example 1 on page 100 can be expressed in the form h(t) = − 16(t − 4)(t + 2), t ≥ 0. What is the practical interpretation of the factors (t − 4) and (t + 2)? Solution When t = 4, the factor (t − 4) has the value 4 − 4 = 0. So ℎ(4) = − 16(0)(4 + 2) = 0. In practical terms, this means that the ball hits the ground 4 seconds after it is thrown. When t = − 2, the factor (t + 2) has the value − 2 + 2 = 0. However, there is no practical interpretation for this, since the domain of ℎ is t ≥ 0. See Figure 3. 4: Interpretation of the factored form ℎ(t) = − 16(t − 4)(t + 2) Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Interpreting Quadratic Functions Expressed in Factored Form Values of the independent variable where a function has the value zero, such as the t = 4 and t = − 20 in the previous example, are called zeros of the function. In general, we have the following definition. A quadratic function in x is expressed in factored form if it is written as y = f(x) = a(x − r)(x − s), where a, r, and s are constants and a ≠ 0. • The constants r and s are zeros of the function f(x) = a(x − r)(x − s). • The constant a is the leading coefficient, the same as the constant a in the standard form. Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

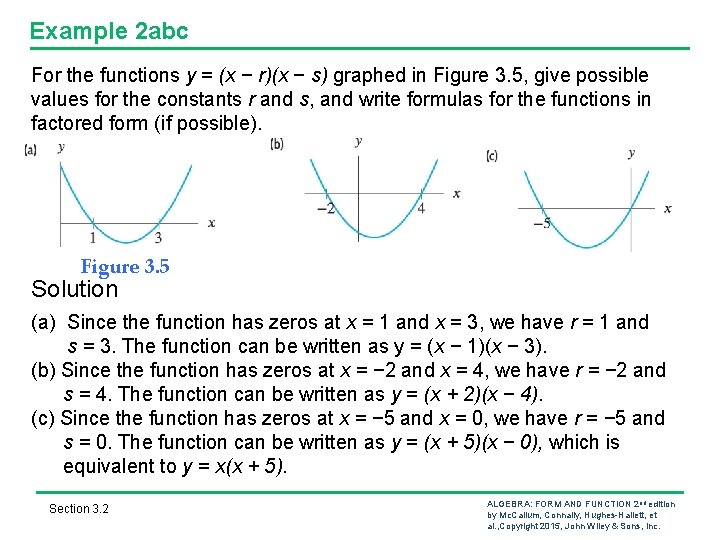
Example 2 abc For the functions y = (x − r)(x − s) graphed in Figure 3. 5, give possible values for the constants r and s, and write formulas for the functions in factored form (if possible). Figure 3. 5 Solution (a) Since the function has zeros at x = 1 and x = 3, we have r = 1 and s = 3. The function can be written as y = (x − 1)(x − 3). (b) Since the function has zeros at x = − 2 and x = 4, we have r = − 2 and s = 4. The function can be written as y = (x + 2)(x − 4). (c) Since the function has zeros at x = − 5 and x = 0, we have r = − 5 and s = 0. The function can be written as y = (x + 5)(x − 0), which is equivalent to y = x(x + 5). Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

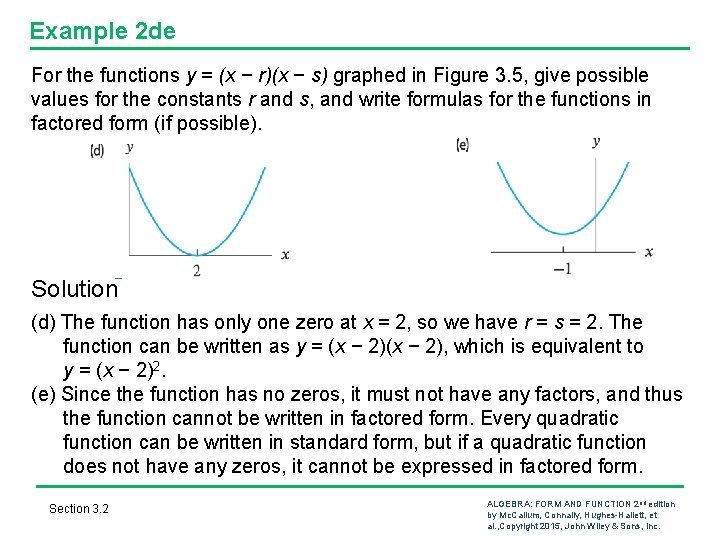
Example 2 de For the functions y = (x − r)(x − s) graphed in Figure 3. 5, give possible values for the constants r and s, and write formulas for the functions in factored form (if possible). Figure 3. 5 Solution (d) The function has only one zero at x = 2, so we have r = s = 2. The function can be written as y = (x − 2), which is equivalent to y = (x − 2)2. (e) Since the function has no zeros, it must not have any factors, and thus the function cannot be written in factored form. Every quadratic function can be written in standard form, but if a quadratic function does not have any zeros, it cannot be expressed in factored form. Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 3 A college bookstore finds that if it charges p dollars for a T-shirt, it sells 1000 − 20 p T-shirts. Its revenue is the product of the price and the number of T-shirts it sells. (a) Express its revenue R(p) as a quadratic function of the price p in factored form. (b) For what prices is the revenue equal to zero? Solution (a) The revenue R(p) at price p is given by Revenue = R(p) = (Price)(Number sold) = p(1000 − 20 p). Factoring − 20 from each term in 1000 − 20 p, we have R(p) = − 20 p(− 50 + p) = − 20 p(p − 50). (b) The revenue has factors p and p− 50. From the first factor, we see the revenue is zero when p = 0. This makes sense since if the bookstore does not charge any money for the T-shirt, it does not earn any revenue. From the second factor, we see the revenue is also zero when p = 50. If the price of a T-shirt is p = 50, then the number of T-shirts the bookstore sells is 1000− 20(50) = 0. The T-shirts are so expensive that nobody is willing to buy them. Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

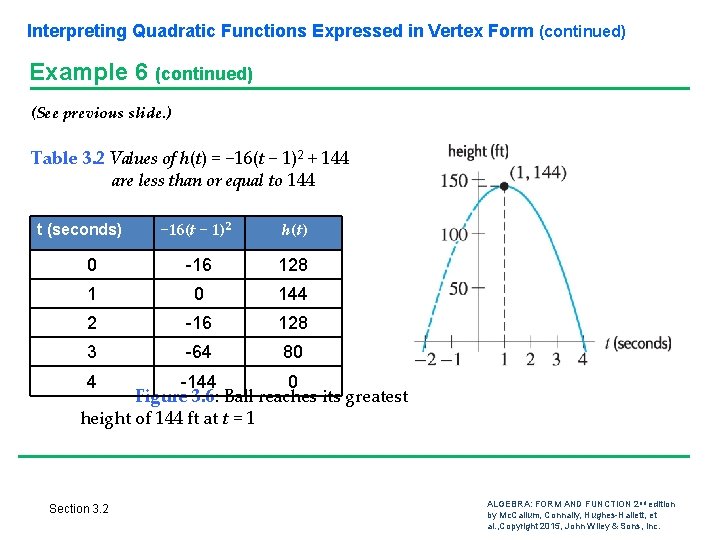
Interpreting Quadratic Functions Expressed in Vertex Form Example 4 The function h(t) = − 16 t 2 + 32 t + 128 in Example 1 can be expressed in the form h(t) = − 16(t − 1)2 + 144. Use this form to show that the ball reaches its maximum height h = 144 when t = 1. Solution Looking at the right-hand side, we see that the term − 16(t − 1)2 is a negative number times a square, so it is always negative or zero, and it is zero when t = 1. Therefore h(t) is always less than or equal to 144 and is equal to 144 when t = 1. This means the maximum height the ball reaches is 144 feet, and it reaches that height after 1 second. See Table 3. 2 and Figure 3. 6. (See next slide for Table 3. 2 and Figure 3. 6. ) Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Interpreting Quadratic Functions Expressed in Vertex Form (continued) Example 6 (continued) (See previous slide. ) Table 3. 2 Values of h(t) = − 16(t − 1)2 + 144 are less than or equal to 144 − 16(t − 1)2 h(t) 0 -16 128 1 0 144 2 -16 128 3 -64 80 t (seconds) 4 -144 0 Figure 3. 6: Ball reaches its greatest height of 144 ft at t = 1 Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Interpreting Quadratic Functions Expressed in Vertex Form (continued) The point (1, 144) in Figure 3. 6 is called the vertex of the graph. For quadratic functions the vertex shows where the function reaches either its largest value, called the maximum, or its smallest value, called the minimum. In Example 4 the function reaches its maximum value at the vertex because the coefficient is negative in the term − 16(t − 1)2. A quadratic function in x is expressed in vertex form if it is written as y = f(x) = a(x − h)2 + k, where a, h, and k are constants and a ≠ 0. For the function f(x) = a(x − h)2 + k, • f(h) = k, and the point (h, k) is the vertex of the graph. • The coefficient a is the leading coefficient, the same a as in the standard form. ・ If a > 0 then k is the minimum value of the function, and the graph opens upward. ・ If a < 0 then k is the maximum value of the function, and the graph opens downward Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

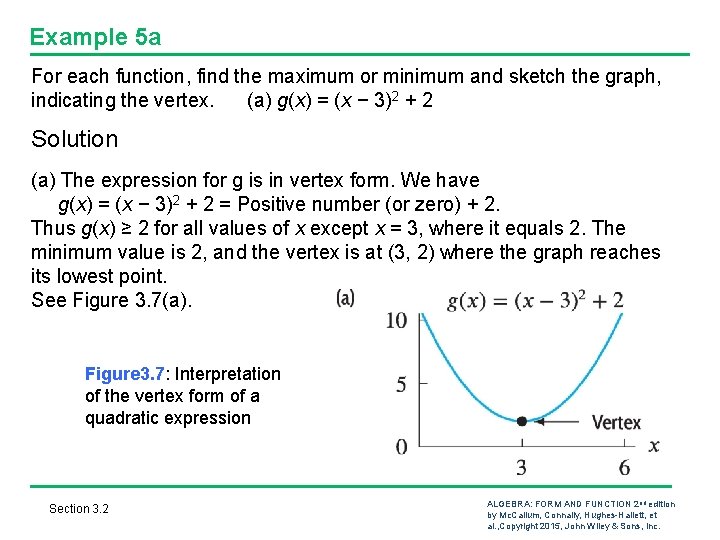
Example 5 a For each function, find the maximum or minimum and sketch the graph, indicating the vertex. (a) g(x) = (x − 3)2 + 2 Solution (a) The expression for g is in vertex form. We have g(x) = (x − 3)2 + 2 = Positive number (or zero) + 2. Thus g(x) ≥ 2 for all values of x except x = 3, where it equals 2. The minimum value is 2, and the vertex is at (3, 2) where the graph reaches its lowest point. See Figure 3. 7(a). Figure 3. 7: Interpretation of the vertex form of a quadratic expression Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

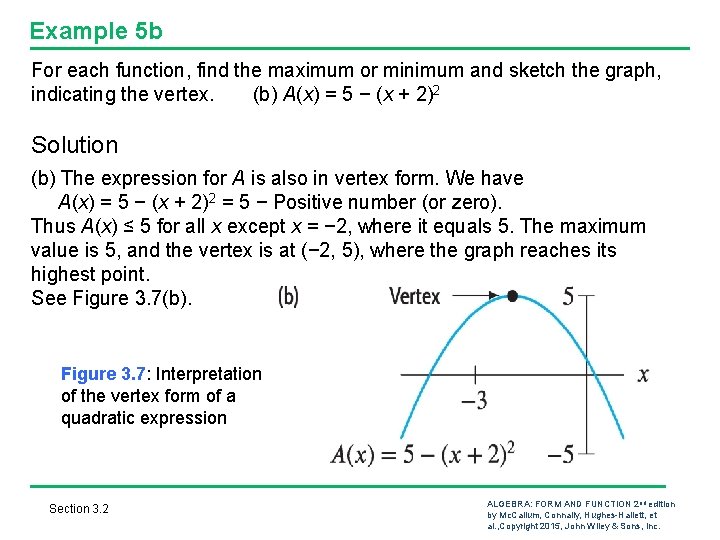
Example 5 b For each function, find the maximum or minimum and sketch the graph, indicating the vertex. (b) A(x) = 5 − (x + 2)2 Solution (b) The expression for A is also in vertex form. We have A(x) = 5 − (x + 2)2 = 5 − Positive number (or zero). Thus A(x) ≤ 5 for all x except x = − 2, where it equals 5. The maximum value is 5, and the vertex is at (− 2, 5), where the graph reaches its highest point. See Figure 3. 7(b). Figure 3. 7: Interpretation of the vertex form of a quadratic expression Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

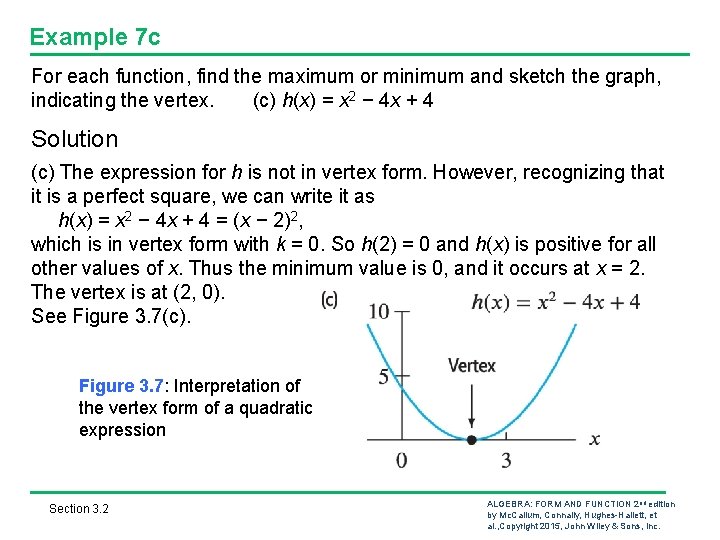
Example 7 c For each function, find the maximum or minimum and sketch the graph, indicating the vertex. (c) h(x) = x 2 − 4 x + 4 Solution (c) The expression for h is not in vertex form. However, recognizing that it is a perfect square, we can write it as h(x) = x 2 − 4 x + 4 = (x − 2)2, which is in vertex form with k = 0. So h(2) = 0 and h(x) is positive for all other values of x. Thus the minimum value is 0, and it occurs at x = 2. The vertex is at (2, 0). See Figure 3. 7(c). Figure 3. 7: Interpretation of the vertex form of a quadratic expression Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Constructing Quadratic Expressions The standard form tells us the vertical intercept, the factored form tells us the horizontal intercepts, and the vertex form tells us the maximum or minimum value of the function. We can also go the other way and use this information to construct an expression for a given quadratic function. Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

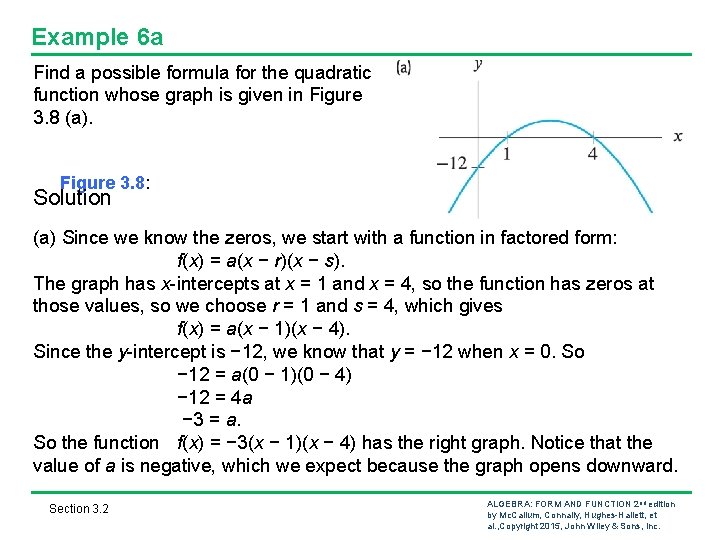
Example 6 a Find a possible formula for the quadratic function whose graph is given in Figure 3. 8 (a). Figure 3. 8: Solution (a) Since we know the zeros, we start with a function in factored form: f(x) = a(x − r)(x − s). The graph has x-intercepts at x = 1 and x = 4, so the function has zeros at those values, so we choose r = 1 and s = 4, which gives f(x) = a(x − 1)(x − 4). Since the y-intercept is − 12, we know that y = − 12 when x = 0. So − 12 = a(0 − 1)(0 − 4) − 12 = 4 a − 3 = a. So the function f(x) = − 3(x − 1)(x − 4) has the right graph. Notice that the value of a is negative, which we expect because the graph opens downward. Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 6 b Find a possible formula for the quadratic function whose graph is given in Figure 3. 8 (b). Figure 3. 8: Solution (b) We are given the vertex of the parabola, so we try to write its equation using the vertex form y = f(x) = a(x − h)2 + k. Since the coordinates of the vertex are (3, − 13), we let h = 3 and k = − 13. This gives f(x) = a(x − 3)2 − 13. The y-intercept is (0, 5), so we know that y = 5 when x = 0. Substituting, we get 5 = a(0 − 3)2 − 13 5 = 9 a − 13 18 = 9 a 2 = a. Therefore, the function f(x) = 2(x − 3)2 − 13 has the correct graph. Notice that the value of a is positive, which we expect because the graph opens upward. Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 2 WORKING WITH QUADRATIC EXPRESSIONS Key Points • The factored form shows where the function is equal to zero • The vertex form shows where the function reaches its maximum or minimum • Constructing quadratic expressions Section 3. 2 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 3 Converting to Factored and Vertex Form Section 3. 3 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Converting Quadratic Expressions to Standard and Factored Form In the previous section we saw three forms for a function giving the height of a ball: h(t) = − 16 t 2 + 32 t + 128 (standard form) = − 16(t − 4)(t + 2) (factored form) = − 16(t − 1)2 + 144 (vertex form). One way to see that these forms are equivalent is to convert them all to standard form. Section 3. 3 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Converting to Factored Form Example 1 If possible, express the quadratic function in factored form. (a) f(x) = x 2 − 2 x − 15 (b) g(t) = 2 t 2 − 16 t + 14 Solution (a) To factor x 2 − 2 x− 15, we write − 2 x as a sum of two terms whose coefficients multiply to − 15. Writing − 2 x = − 5 x + 3 x works since − 5 ⋅ 3 = − 15. This gives f(x) = x 2 − 2 x − 15 = x 2 − 5 x + 3 x − 15 = (x 2 − 5 x) + (3 x − 15) = x(x − 5) + 3(x − 5) = (x + 3)(x − 5). (b) First we take out the common factor of 2 from 2 t 2 − 16 t + 14. This gives 2 t 2 − 16 t + 14 = 2(t 2 − 8 t + 7). To factor t 2− 8 t+7, we write − 8 t as a sum of two terms whose coefficients multiply to 7. Writing − 8 t = − 7 t − t works since − 7 ⋅ (− 1) = 7. This gives g(t) = 2(t 2 − 8 t + 7) = 2(t 2 − 7 t − t + 7) = 2 ((t 2 − 7 t) + (−t + 7)) = 2(t(t − 7) − (t − 7)) = 2(t − 7)(t − 1). Section 3. 3 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

How Do We Put an Expression in Vertex Form? The key to putting an expression in vertex form is recognizing a quadratic expression that is a perfect square—that is, in the following form: (x + p)2 = x 2 + 2 px + p 2. For example, in looking at the function y = x 2 + 6 x + 9 we recognize that x 2 + 6 x + 9 = x 2 + 2 ⋅ 3 x + 32, so p = 3 and y = x 2 + 6 x + 9 = (x + 3)2. When we have an expression that is not a perfect square, such as x 2 + 6 x + 8 , we can put it in vertex form by first transforming it into a perfect square. Starting with y = x 2 + 6 x + 8 we recognize that adding 1 to both sides leads to y + 1 = x 2 + 6 x + 9 = (x + 3)2. Finally, subtracting 1 from both sides gives the vertex form y = (x + 3)2 − 1. Because we added a constant that made the right-hand side into a perfect square, this process is called completing the square. Section 3. 3 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

How Do We Put an Expression in Vertex Form? (continued) Example 3 Express the function in vertex form by completing the square: y = 4 z 2 − 40 z + 16. Solution We first divide both sides by 4, the value of the leading coefficient of the expression on the right-hand side. This gives y/4 = (4 z 2 − 40 z + 16)/4 = z 2 − 10 z + 4. For the z-terms to match we must have 2 p = − 10, so p = − 5, and p 2 = 25. To get a 25 on the right-hand side we add 21 to both sides: y/4 + 21 = z 2 − 10 z + 25 = (z − 5)2. Finally, to write the function in vertex form we solve for y: y/4 + 21 = (z − 5)2 y/4 = (z − 5)2 − 21 y = 4((z − 5)2 − 21) y = 4(z − 5)2 − 84. Section 3. 3 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

To find the maximum or minimum value of a quadratic function, we can use the method of completing the square to express the function in vertex form. Example 7 A bookstore finds that if it charges $p for a T-shirt then its revenue from T-shirt sales is given by R = f(p) = p(1000 − 20 p) What price should it charge in order to maximize the revenue? Solution We first expand the revenue function into standard form: R = f(p) = p(1000 − 20 p) = 1000 p − 20 p 2. Since the coefficient of p 2 is − 20, we know the graph of the quadratic opens downward. So the vertex form of the equation gives us its maximum value. R = 1000 p − 20 p 2 −R/20 = p 2 − 50 p divide by − 20 add 252 to both sides −R/20 + 252 = p 2 − 50 p + 252 −R/20 + 252 = (p − 25)2 (Solution continued on next slide. ) Section 3. 3 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

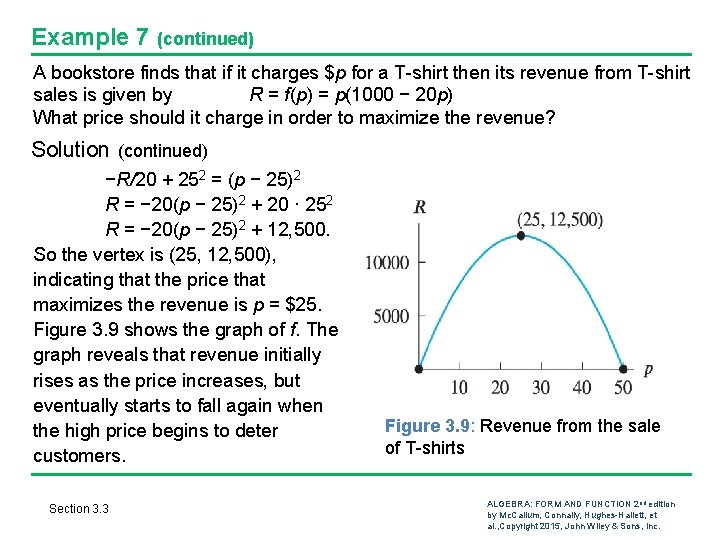
Example 7 (continued) A bookstore finds that if it charges $p for a T-shirt then its revenue from T-shirt sales is given by R = f(p) = p(1000 − 20 p) What price should it charge in order to maximize the revenue? Solution (continued) −R/20 + 252 = (p − 25)2 R = − 20(p − 25)2 + 20 · 252 R = − 20(p − 25)2 + 12, 500. So the vertex is (25, 12, 500), indicating that the price that maximizes the revenue is p = $25. Figure 3. 9 shows the graph of f. The graph reveals that revenue initially rises as the price increases, but eventually starts to fall again when the high price begins to deter customers. Section 3. 3 Figure 3. 9: Revenue from the sale of T-shirts ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

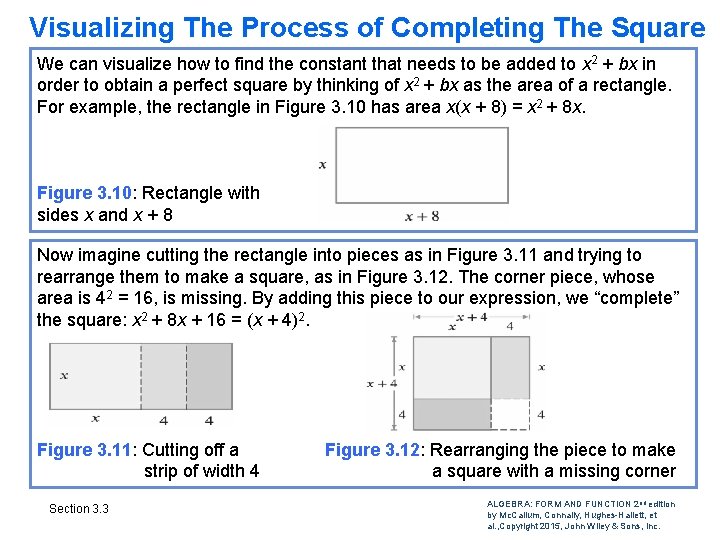
Visualizing The Process of Completing The Square We can visualize how to find the constant that needs to be added to x 2 + bx in order to obtain a perfect square by thinking of x 2 + bx as the area of a rectangle. For example, the rectangle in Figure 3. 10 has area x(x + 8) = x 2 + 8 x. Figure 3. 10: Rectangle with sides x and x + 8 Now imagine cutting the rectangle into pieces as in Figure 3. 11 and trying to rearrange them to make a square, as in Figure 3. 12. The corner piece, whose area is 42 = 16, is missing. By adding this piece to our expression, we “complete” the square: x 2 + 8 x + 16 = (x + 4)2. Figure 3. 11: Cutting off a strip of width 4 Section 3. 3 Figure 3. 12: Rearranging the piece to make a square with a missing corner ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 3 WORKING WITH QUADRATIC EXPRESSIONS Key Points • Converting to factored form to show zeros. • Converting to vertex form to show where the function reaches its maximum or minimum • Completing the square procedure Section 3. 3 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 4 Quadratic Equations Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

When we find the zeros of a quadratic function f(x) = ax 2 + bx + c, we are solving the equation ax 2 + bx + c = 0. A quadratic equation in x is one which can be put into the standard form ax 2 + bx + c = 0, where a, b, c are constants, with a ≠ 0. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Solving Quadratic Equations by Factoring The zero-factor principle states that If A · B = 0 then either A = 0 or B = 0 (or both). The factors A and B can be any numbers, including those represented by algebraic expressions. In Example 3 on page 105 we considered the quadratic function which gives the revenue of selling T-shirts at price p dollars, R(p) = p(1000 − 20 p). Since this function is already given as a product of linear factors, we can find its zeros by finding where the factors are zero. According to the zero-factor principle, the only possibilities for R(p) = p(1000 − 20 p) = 0 are for p = 0 or 1000 – 20 p = 0 This gives the solutions p = 0 and p = 50. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 1 a Solve the quadratic equations using the zero-factor principle and factoring. (a) x 2 − 4 x + 3 = 0 Solution (a) We have f(x) = x 2 − 4 x + 3 = (x − 1)(x − 3), so x = 1 and x = 3 are zeros. To see that they are the only zeros, we let A = x − 1 and B = x − 3, and we apply the zero-factor principle. If x is a zero, then so either A = 0, which implies x − 1 = 0 x = 1, or B = 0, which implies x − 3 = 0 x = 3. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 1 b Solve the quadratic equations using the zero-factor principle and factoring. (b) 3 x 2 + 3 x = 6 Solution (b) In order to use the zero-factor principle, we must first write the quadratic equation in the standard form by subtracting 6 from both sides. This gives 3 x 2 + 3 x − 6 = 0 x 2 + x − 2 = 0 divide both sides by 3 (x + 2)(x − 1) = 0. This implies x = − 2 and x = 1 are the solutions. In general, the zero-factor principle tells us that for a quadratic equation in the form a(x − r)(x − s) = 0, where a, r, s are constants, a ≠ 0, the only solutions are x = r and x = s. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Solving Quadratic Equations with Perfect Squares Example 2 ab Solve the quadratic equation by taking square roots of both sides (if possible). (a) x 2 − 4 = 0 (b) x 2 − 5 = 0 Solution (a) Rewriting the equation as we see the solutions are x 2 = 4, (b) Similarly, the solutions to x 2 − 5 = 0 are We can use the result of Example 2 b to solve (x − 2)2 = 5. Since the equation x 2 = 5 has solutions , the equation (x − 2)2 = 5 has solutions Thus the solutions to (x − 2)2 = 5 are which can be combined as Using a calculator, these solutions are approximately x = 2 + 2. 236 = 4. 236 and x = 2 − 2. 236 = − 0. 236. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

In general, if we can put a quadratic equation in the form (x − h)2 = Constant, then we can solve it by taking square roots of both sides. Example 2 cd Solve the quadratic equation by taking square roots of both sides (if possible). (a) 2(y + 1)2 = 0 (b) 2(y − 3)2 + 4 = 0. Solution (a) Since 2(y + 1)2 = 0, dividing by 2 gives (y + 1)2 = 0 so y + 1 = 0. Thus the only solution is y = − 1. It is possible for a quadratic equation to have only one solution. (b) Since 2(y − 3)2 + 4 = 0, we have 2(y − 3)2 = − 4, so dividing by 2 gives (y − 3)2 = − 2. But since no number squared is − 2, this equation has no real number solutions. Example 2 illustrates that it is possible for a quadratic equation to have two solutions, just one solution, or no solution. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 3 The height of a ball t seconds after it is thrown is h(t) = 16 t 2 +32 t + 128 = − 16(t − 1)2 + 144 Find the times where the ball reaches a height of 135 feet. Solution We want to find the values of t such that h(t) = 135, so we want to solve the equation with the perfect square − 16(t − 1)2 + 144 = 135. Isolating the (t − 1)2 term we get Therefore, the solutions are t = 0. 25 and t = 1. 75. So the ball reaches a height of 135 ft on its way up very soon after being thrown and again on its way down about 2 seconds after being thrown. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Solving Quadratic Equations by Completing the Square Example 4 a Solve the quadratic equation by completing the square: (a) x 2 + 6 x + 8 = 1. Solution First, we move the constant to the right by adding − 8 to both sides: x 2 + 6 x + 8 − 8 = 1 − 8 add − 8 to each side x 2 + 6 x = − 7 x 2 + 6 x + 9 = − 7 + 9 complete the square by adding (6/2)2 = 9 to both sides (x + 3)2 = 2 taking the square root of both sides and solving for x Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Solving Quadratic Equations by Completing the Square If the coefficient of x 2 is not 1 we can divide through by it before completing the square. Example 4 b Solve the quadratic equation by completing the square: (b) 3 x 2 + 6 x − 2 = 0 . Solution First, divide both sides of the equation by 3: x 2 + 2 x − 2/3 = 0. Next, move the constant to the right by adding 2/3 to both sides: x 2 + 2 x = 2/3. Now complete the square. The coefficient of x is 2, and half this is 1, so we add 12 = 1 to each side to complete the square: x 2 + 2 x + 1 = 2/3 + 1 or (x + 1)2 = 5/3 Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

The Quadratic Formula Completing the square on the equation ax 2 + bx + c = 0 gives a formula for the solution of any quadratic equation. First we divide by a, getting Now subtract the constant c/a from both sides: We complete the square by adding a constant to both sides of the equation. The coefficient of x is b/a, and half this is (Continued on next slide. ) Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

The Quadratic Formula (continued) We square this and add the result, (b/2 a)2, to each side: complete the square expand parentheses find a common denominator simplify right-hand side. (Continued on next slide. ) Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

The Quadratic Formula (continued) We now rewrite the left-hand side as a perfect square: Taking square roots gives So which gives the solutions Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

The Quadratic Formula (continued) The quadratic formula combines both solutions of ax 2 + bx + c = 0: Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 5 a Use the quadratic formula to solve for x: (a) 2 x 2 − 2 x − 7 = 0 Solution (a) We have a = 2, b = − 2, c = − 7, so Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 5 b Use the quadratic formula to solve for x: (b) 3 x 2 + 3 x = 10 Solution (b) We first put the equation in standard form by subtracting 10 from both sides: 3 x 2 + 3 x − 10 = 0. Thus a = 3, b = 3, and c = − 10, so Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 6 The distance it takes a driver to stop in an emergency is the sum of the reaction distance (the distance traveled while the driver is reacting to the emergency) and the braking distance (the distance traveled once the driver has put on the brakes). For a car traveling at v km/hr, the reaction distance is 0. 42 v meters and the stopping distance is 0. 0085 v 2 meters. What is the speed of a car that stops in 100 meters? Solution The total stopping distance is 0. 42 v + 0. 0085 v 2 meters, so we want to solve the equation 0. 42 v + 0. 0085 v 2 = 100, or, in standard form, 0. 0085 v 2 + 0. 42 v − 100 = 0. Using the quadratic formula, we get The positive root is the only one that makes sense in this context, so the car was going about 87 km/hr. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

The Discriminant We can tell how many solutions a quadratic equation has without actually solving the equation. Look at the expression, b 2 − 4 ac, under the square root sign in the quadratic formula. For the equation ax 2 + bx + c = 0, we call D = b 2 − 4 ac the discriminant • If D = b 2 − 4 ac is positive, then has two different values, so the quadratic equation has two distinct solutions (roots). • If D = b 2 − 4 ac is negative, then is the square root of a negative number, so the quadratic equation has no real solutions. 2 − 4 ac = 0, then so the quadratic equation • If D = b has only one solution. This is sometimes referred to as a repeated root. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 7 How many solutions does each equation have? (a) 4 x 2 − 10 x + 7 = 0 (b) 0. 3 w 2 + 1. 5 w + 1. 8 = 0 (c) 3 t 2 − 18 t + 27 = 0 Solution (a) We use the discriminant. In this case, a = 4, b = − 10, and c = 7. The value of the discriminant is thus b 2 − 4 ac = (− 10)2 − 4 · 7 = 100 − 112 = − 12. Since the discriminant is negative, we know that the quadratic equation has no real solutions. (b) We again use the discriminant. In this case, a = 0. 3, b = 1. 5, and c = 1. 8. The value of the discriminant is thus b 2 − 4 ac = (1. 5)2 − 4 · 0. 3 · 1. 8 = 0. 09. Since the discriminant is positive, we know that the quadratic equation has two distinct solutions. (c) Checking the discriminant, we find b 2 − 4 ac = (− 18)2 − 4 · 3 · 27 = 0. Since the discriminant is zero, we know that the quadratic equation has only one solution. Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 4 SOLVING QUADRATIC EQUATIONS Key Points • Solving quadratic equations by factoring • Solving equations by taking square roots • Solving equations by completing the square • Using the quadratic formula to solve quadratic equations • The discriminant Section 3. 4 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 5 Factoring Hidden Quadratics Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 1 abc The revenue to a bookstore from selling 1000 − 20 p T-shirts at p dollars each is R(p) = p(1000 − 20 p). Suppose that each T-shirt costs the bookstore $3 to make. (a) Write an expression for the cost of making the T-shirts. (b) Write an expression for the profit, which is the revenue minus the cost. (c) For what values of p is the profit positive? Solution (a) Since each T-shirt costs $3 to make, we have Cost = 3(Number of T-shirts sold) = 3(1000 − 2 p). (b) We have Profit = Revenue − Cost = p(1000 − 20 p) − 3(1000 − 20 p). (c) Factored form is the most useful for answering this question. We do not need to expand the expression into standard form before trying to factor since we see there is a common factor of 1000 − 20 p. Taking out this factor, we get Profit = p(1000 − 20 p) − 3(1000 − 20 p) = (p − 3)(1000 − 20 p) = 20(p − 3)(50 − p). (Continued on next slide. ) Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 1 cd (continued) The revenue to a bookstore from selling 1000 − 20 p T-shirts at p dollars each is R(p) = p(1000 − 20 p). Suppose that each T-shirt costs the bookstore $3 to make. (c) For what values of p is the profit positive? (d) Interpret your answer in practical terms. Solution (c) Profit = p(1000 − 20 p) − 3(1000 − 20 p) = (p − 3)(1000 − 20 p) = 20(p − 3)(50 − p). This first factor is p − 3, which is positive when p > 3 and negative when p < 3. So p > 50 ∶ g(p) = 20(p − 3)(50 − p) = Positive × Negative = Nega 3 < p < 50 ∶ g(p) = 20(p − 3)(50 − p) = Positive × Positive = Posit p<3∶ g(p) = 20(p − 3)(50 − p) = Negative × Positive = N So the profit is positive only if the price is greater than $3 but less than $50. (d) The bookstore has to sell the T-shirts for more than it costs to make them, so that is why the price has to be greater than $3. But if it charges too much then nobody will buy the T-shirts. Since the number it can sell at price p is 1000− 20 p, it prices itself out of the market when 1000− 20 p = 0, which means p = 50. That is why the price has to be less than $50. Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 2 b Solve the equation using the zero-factor principle and factoring: (b) 2 x 3 − 5 x 2 = 3 x Solution (b) In order to use the zero-factor principle, we first subtract 3 x from both sides. Then we factor the expression on the left-hand side: 2 x 3 − 5 x 2 − 3 x = 0 x(2 x 2 − 5 x − 3) = 0 factor out an x x(2 x + 1)(x − 3) = 0. factor the quadratic If the product of three numbers is 0, then at least one of them must be 0. Thus x = 0 or 2 x + 1 = 0 or x − 3 = 0, so x = 0 or x = − 1/2 or x = 3. We call 2 x 3 − 5 x 2 − 3 x = 0 a cubic equation, because the highest power of x is 3. Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 3 Solve y 4 − 10 y 2 + 9 = 0. Solution Since y 4 = (y 2)2, the equation can be written as y 4 − 10 y 2 + 9 = (y 2)2 − 10 y 2 + 9 = 0. We can think of this as a quadratic equation in y 2. Letting z = y 2, we get z 2 − 10 z + 9 = 0 replacing y 2 with z (z − 1)(z − 9) = 0 factoring the left side (y 2 − 1)(y 2 − 9) = 0 replacing z with y 2. Thus, the solutions are given by y 2 − 1 = 0 or y 2 − 9 = 0. Solving for y gives y = ± 1 or y = ± 3 The equation y 4 − 10 y 2 + 9 = 0 is called a quartic equation because the highest power of y is 4. Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Sometimes an equation that does not look like a quadratic equation can be transformed into one. We must be careful to check our answers after making a transformation, because sometimes the transformed equation has solutions that are not solutions to the original equation. Example 4 Solve Solution Multiplying both sides by a(a − 1) gives Canceling (a − 1) on the left and a on the right, we get a 2 = 4(a − 1), giving the quadratic equation a 2 − 4 a + 4 = 0. Factoring gives (a − 2)2 = 0, which has solution a = 2. Since we multiplied both sides by a factor that could be zero, we check the solution: Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 5 Solve Solution Notice that the two equal fractions have the same denominator. Therefore, it will suffice to find the values of x that make the numerators equal, provided that such values do not make the denominator zero. x 2 − 1 = 8 Rewriting this equation as x 2 = 9 and taking the square root of both sides, we see that x = 3 and x = − 3. The denominator of the original equation, x + 3, is not zero when x = 3. Therefore, it is a solution to the original equation. However, the denominator in the original equation is zero when x = − 3. This means that x = − 3 is not a solution to the original equation. So x = − 3 is an extraneous solution that was introduced during the solving procedure. Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 5 FACTORING HIDDEN QUADRATICS Key Points • Solving and interpreting equations by factoring • Solving other equations using quadratic equations Section 3. 5 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 6 Complex Numbers Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Until now, we have been regarding expressions like as undefined, because there is no real number whose square is − 4. In this section, we expand our idea of number to include complex numbers. In the system of complex numbers, there is a number whose square is − 4. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Using Complex Numbers to Solve Equations The general solution of cubic equations was discovered during the sixteenth century. The solution introduced square roots of negative numbers, called imaginary numbers. This discovery led mathematicians to find the solutions of quadratic equations, such as x 2 − 2 x + 10 = 0, which is not satisfied by any real number x. Applying the quadratic formula gives The number − 36 does not have a square root which is a real number. To overcome this problem, we define the imaginary number Then i 2 = − 1. Using i, we see that (6 i)2 = 36 i 2 = − 36, so There are two solutions for this quadratic equation just as there were two solutions in the case of real numbers. The numbers 1 + 3 i and 1 − 3 i are examples of complex numbers. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Using Complex Numbers to Solve Equations A complex number is defined as any number that can be written in the form z = a + bi, where a and b are real numbers and The real part of z is the number a; the imaginary part is the number bi. Calling the number i imaginary makes it sound as though i does not exist in the same way as real numbers exist. In practice, if we measure mass or position, we want our answers to be real. However, there are real world phenomena, such as electro-magnetic waves, which are described using complex numbers. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 1 Solve x 2 − 6 x + 15 = 4. Solution To solve this equation, we put it in the form ax 2 + bx + c = 0. x 2 − 6 x + 15 = 4 x 2 − 6 x + 11 = 0. Applying the quadratic formula gives Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Algebra of Complex Numbers We can perform operations on complex numbers much like on real numbers. Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. That is, a + bi = c + di means that a = c and b = d. In particular, the equality a + bi = 0 is equivalent to a = 0, b = 0. A complex number with an imaginary part equal to zero is a real number. Two complex numbers are called conjugates if their real parts are equal and if their imaginary parts differ only in sign. The complex conjugate of the complex number z = a + bi is denoted . So (Note that z is real if and only if ). Section 3, 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 2 What is the conjugate of 5 − 7 i? Solution To find the conjugate, we simply change the subtraction sign to an addition sign. The conjugate of 5 − 7 i is 5 + 7 i. Example 3 Find the real numbers a and b that will make the following equation true: 2 − 6 i = 2 a + 3 bi. Solution For the equation to be true, we must have 2 a = 2 and 3 bi = − 6 i. Thus, a = 1 and 3 b = − 6, which gives us b = − 2. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Addition and Subtraction of Complex Numbers To add two complex numbers, we add the real and imaginary parts separately: (a + bi) + (c + di) = (a + c) + (b + d)i. Subtracting one complex number from another is similar: (a + bi) − (c + di) = (a − c) + (b − d)i. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 4 Compute the sum (2 + 7 i) + (3 − 5 i). Solution Adding real and imaginary parts gives (2 + 7 i) + (3 − 5 i) = (2 + 3) + (7 i − 5 i) = 5 + 2 i. Example 5 Compute the difference (5 − 4 i) − (8 − 3 i). Solution Subtracting real and imaginary parts gives (5 − 4 i) − (8 − 3 i) = (5 − 8) + (− 4 i − (− 3 i)) = (5 − 8) + (− 4 i + 3 i) = − 3 − i. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Multiplication of Complex Numbers Multiplication of complex numbers follows the distributive law. We use the identity i 2 = − 1 and separate the real and imaginary parts to expand the product (a + bi)(c + di): (a + bi)(c + di) = a(c + di) + bi(c + di) = ac + adi + bci + bdi 2 = ac + bd(− 1) + adi + bci = ac − bd + adi + bci = (ac − bd) + (ad + bc)i. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 6 Compute the product (4 + 6 i)(5 + 2 i). Solution Multiplying out gives (4 + 6 i)(5 + 2 i) = 20 + 8 i + 30 i + 12 i 2 = 20 + 38 i − 12 = 8 + 38 i. Example 7 Simplify (2 + 4 i)(4 − i) + 6 + 10 i. Solution We wish to obtain a single complex number in the form a + bi. Multiplying out and adding real and imaginary parts separately: (2 + 4 i)(4 − i) + 6 + 10 i = 8 − 2 i + 16 i − 4 i 2 + 6 + 10 i = 14 + 24 i + 4 = 18 + 24 i. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Multiplication of Complex Numbers (continued) Multiplying a number by its complex conjugate gives a real, non-negative number. This property allows us to divide complex numbers easily. Example 8 (a) Compute the product of − 5 + 4 i and its conjugate. (b) Compute where z = a + bi and a, b are real. Solution (a) We have (− 5 + 4 i)(− 5 − 4 i) = 25 + 20 i − 16 i 2 = 25 − 16(− 1) = 25 + 16 = 41. (b) We have 2 + abi − b 2 i 2 = a 2 − b 2(− 1) = a 2 + b 2 Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Multiplication of Complex Numbers A special case of multiplication is the multiplication of i by itself, that is, powers of i. We know that i 2 = − 1; then, i 3 = i · i 2 = −i, and i 4 = (i 2)2 = (− 1)2 = 1. Then i 5 = i · i 4 = i, and so on. That is, for a nonnegative integer n, in takes on only four values. Thus we have Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Example 9 Simplify each of the following. (a) i 34 (b) 3 i 8 + 2 i 21 − 3 i 43 − 4 i 26 Solution Since i 4 = 1, we use this fact to help us simplify. (a) i 34 = i 2 · i 32 = i 2(i 4)8 = (− 1)(1) = − 1 (b) 3 i 8 + 2 i 21 − 3 i 43 − 4 i 26 = 3(i 8) + 2 i · i 20 − 3 i 3 · i 40 − 4 i 2 · i 24 = 3(i 4)2 + 2 i(i 4)5 − 3 i 3(i 4)10 − 4 i 2(i 4)6 = 3(1) + 2 i(1) − 3 i 3(1) − 4 i 2(1) = 3 + 2 i − 3 i 3 − 4 i 2 = 3 + 2 i − 3(−i) − 4(− 1) = 3 + 2 i + 3 i + 4 = 7 + 5 i. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Division of Complex Numbers How can we divide two complex numbers? Even a very simple case such as (2 + i)/(1 − i) does not have an obvious solution. However, suppose that we divide 2 + i by a real number, such as 5. Then we have In order to divide any two complex numbers, we use the complex conjugate to create a division by a real number, since the product of a number and its complex conjugate is always real. Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

Division of Complex Numbers (continued) Example 10 Compute Solution The conjugate of the denominator is 3 − 2 i, so we multiply by (3 − 2 i)/(3 − 2 i). Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.

3. 6 COMPLEX NUMBERS Key Points • Definition of imaginary and complex numbers • Quadratic equations with complex solutions • Algebra of complex numbers Section 3. 6 ALGEBRA: FORM AND FUNCTION 2 nd edition by Mc. Callum, Connally, Hughes-Hallett, et al. , Copyright 2015, John Wiley & Sons, Inc.