Chapter 3 Quadratic Functions and Equations Copyright 2014

  • Slides: 38
Download presentation
Chapter 3 Quadratic Functions and Equations Copyright © 2014, 2010, 2006 Pearson Education, Inc.

Chapter 3 Quadratic Functions and Equations Copyright © 2014, 2010, 2006 Pearson Education, Inc. 1

3. 5 ♦ ♦ ♦ Transformations of Graphs Graph functions using vertical and horizontal

3. 5 ♦ ♦ ♦ Transformations of Graphs Graph functions using vertical and horizontal shifts Graph functions using stretching and shrinking Graph functions using reflections Combine transformations Model data with transformations (optional) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 2

Vertical and Horizontal Shifts We use these two graphs to demonstrate shifts, or translations,

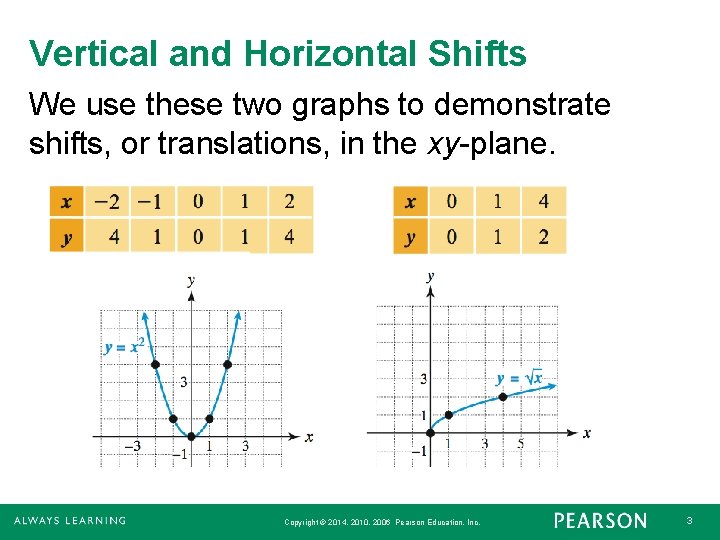
Vertical and Horizontal Shifts We use these two graphs to demonstrate shifts, or translations, in the xy-plane. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 3

Vertical Shifts A graph is shifted up or down. The shape of the graph

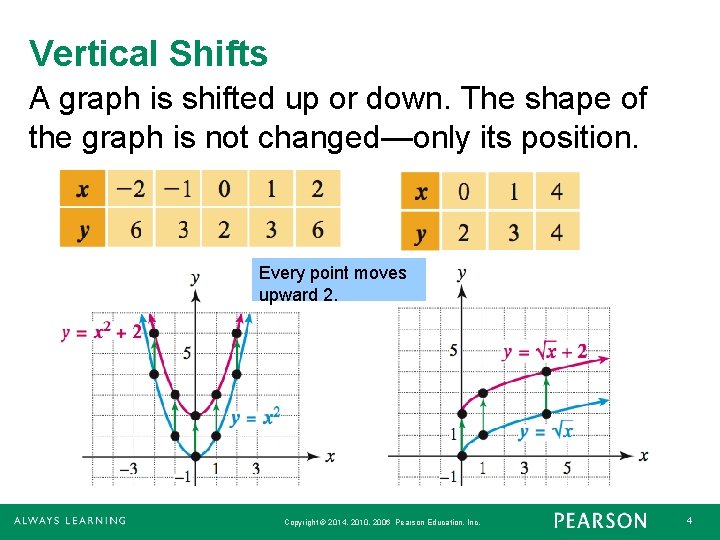
Vertical Shifts A graph is shifted up or down. The shape of the graph is not changed—only its position. Every point moves upward 2. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 4

Horizontal Shifts A graph is shifted right: replace x with (x – 2) Every

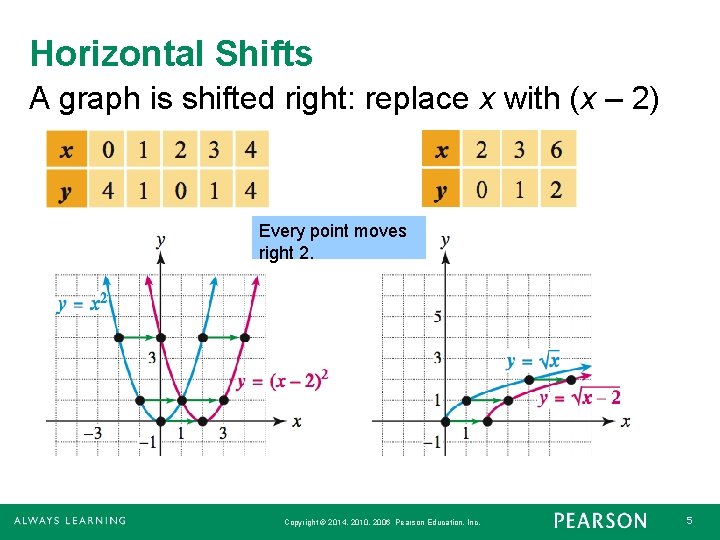
Horizontal Shifts A graph is shifted right: replace x with (x – 2) Every point moves right 2. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 5

Horizontal Shifts A graph is shifted left: replace x with (x + 3), Every

Horizontal Shifts A graph is shifted left: replace x with (x + 3), Every point moves left 3. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 6

Vertical and Horizontal Shifts Let f be a function, and let c be a

Vertical and Horizontal Shifts Let f be a function, and let c be a positive number. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 7

Combining Shifts can be combined to translate a graph of y = f(x) both

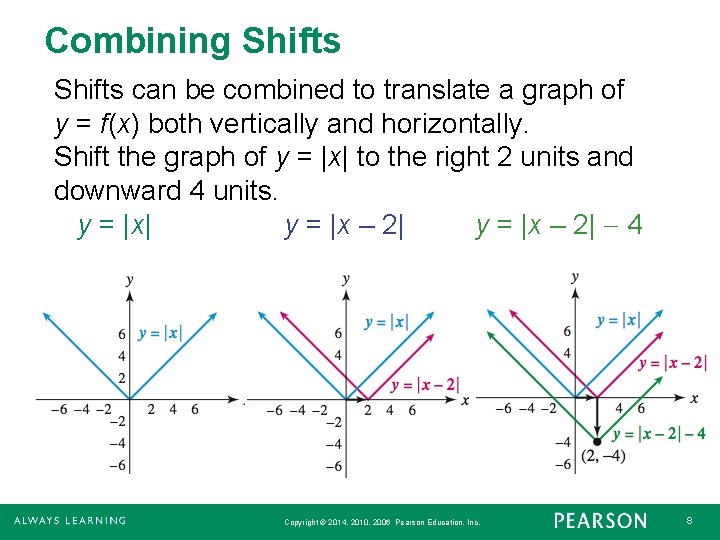
Combining Shifts can be combined to translate a graph of y = f(x) both vertically and horizontally. Shift the graph of y = |x| to the right 2 units and downward 4 units. y = |x| y = |x – 2| 4 Copyright © 2014, 2010, 2006 Pearson Education, Inc. 8

Example: Combining vertical and horizontal shifts Complete the following. (a) Write an equation that

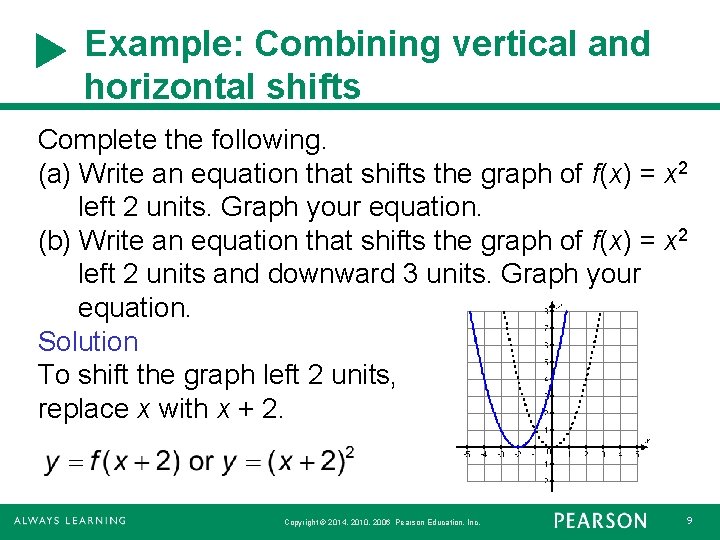
Example: Combining vertical and horizontal shifts Complete the following. (a) Write an equation that shifts the graph of f(x) = x 2 left 2 units. Graph your equation. (b) Write an equation that shifts the graph of f(x) = x 2 left 2 units and downward 3 units. Graph your equation. Solution To shift the graph left 2 units, replace x with x + 2. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 9

Example: Combining vertical and horizontal shifts (b) Write an equation that shifts the graph

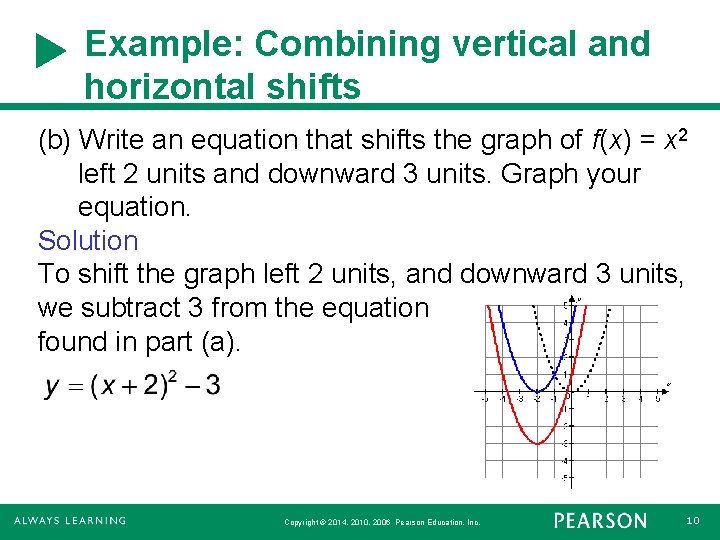
Example: Combining vertical and horizontal shifts (b) Write an equation that shifts the graph of f(x) = x 2 left 2 units and downward 3 units. Graph your equation. Solution To shift the graph left 2 units, and downward 3 units, we subtract 3 from the equation found in part (a). Copyright © 2014, 2010, 2006 Pearson Education, Inc. 10

Vertical Stretching and Shrinking If the point (x, y) lies on the graph of

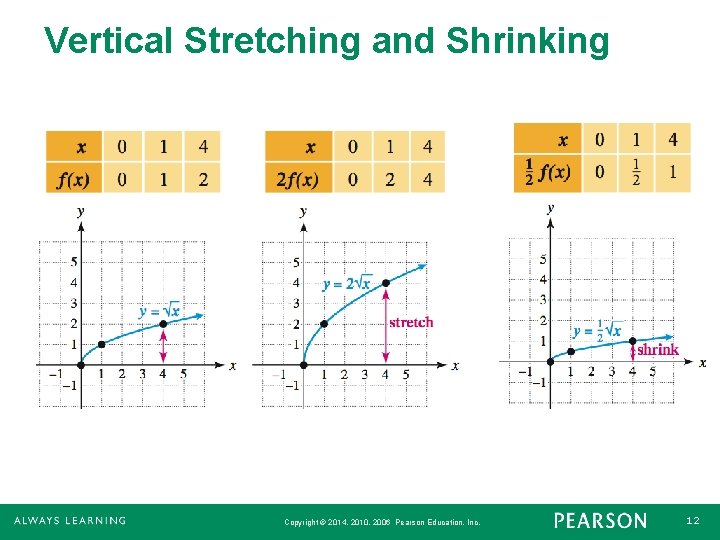
Vertical Stretching and Shrinking If the point (x, y) lies on the graph of y = f(x), then the point (x, cy) lies on the graph of y = cf(x). If c > 1, the graph of y = cf(x) is a vertical stretching of the graph of y = f(x), whereas if 0 < c < 1 the graph of y = cf(x) is a vertical shrinking of the graph of y = f(x). Copyright © 2014, 2010, 2006 Pearson Education, Inc. 11

Vertical Stretching and Shrinking Copyright © 2014, 2010, 2006 Pearson Education, Inc. 12

Vertical Stretching and Shrinking Copyright © 2014, 2010, 2006 Pearson Education, Inc. 12

Horizontal Stretching and Shrinking If the point (x, y) lies on the graph of

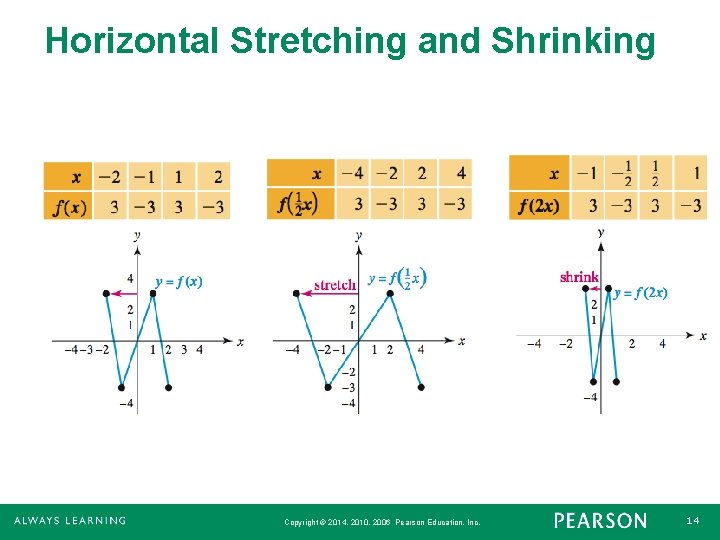
Horizontal Stretching and Shrinking If the point (x, y) lies on the graph of y = f(x), then the point (x/c, y) lies on the graph of y = f(cx). If c > 1, the graph of y = f(cx) is a horizontal shrinking of the graph of y = f(x), whereas if 0 < c < 1 the graph of y = f(cx) is a horizontal stretching of the graph of y = f(x). Copyright © 2014, 2010, 2006 Pearson Education, Inc. 13

Horizontal Stretching and Shrinking Copyright © 2014, 2010, 2006 Pearson Education, Inc. 14

Horizontal Stretching and Shrinking Copyright © 2014, 2010, 2006 Pearson Education, Inc. 14

Example: Stretching and shrinking of a graph Use the graph of y = f(x)

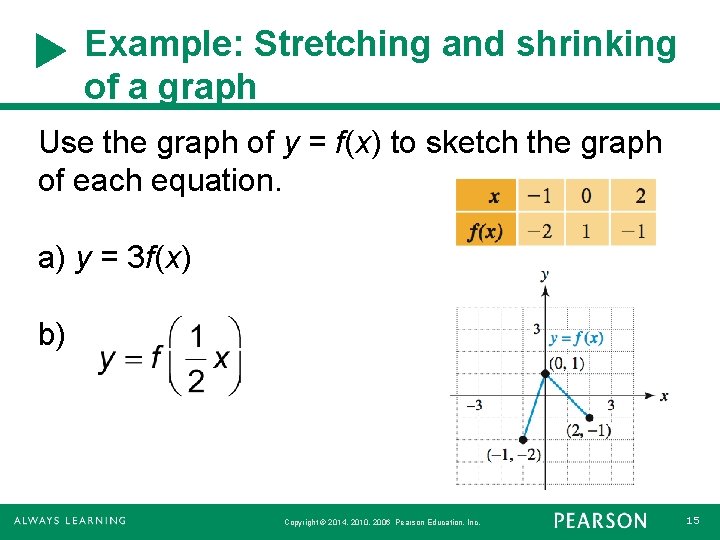
Example: Stretching and shrinking of a graph Use the graph of y = f(x) to sketch the graph of each equation. a) y = 3 f(x) b) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 15

Example: Stretching and shrinking of a graph Solution a) y = 3 f(x) Vertical

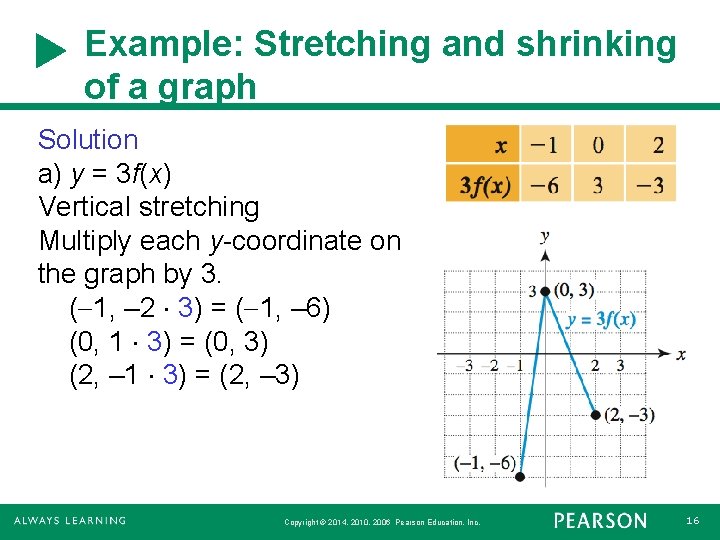
Example: Stretching and shrinking of a graph Solution a) y = 3 f(x) Vertical stretching Multiply each y-coordinate on the graph by 3. ( 1, – 2 3) = ( 1, – 6) (0, 1 3) = (0, 3) (2, – 1 3) = (2, – 3) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 16

Example: Stretching and shrinking of a graph Solution continued b) Horizontal stretching Multiply each

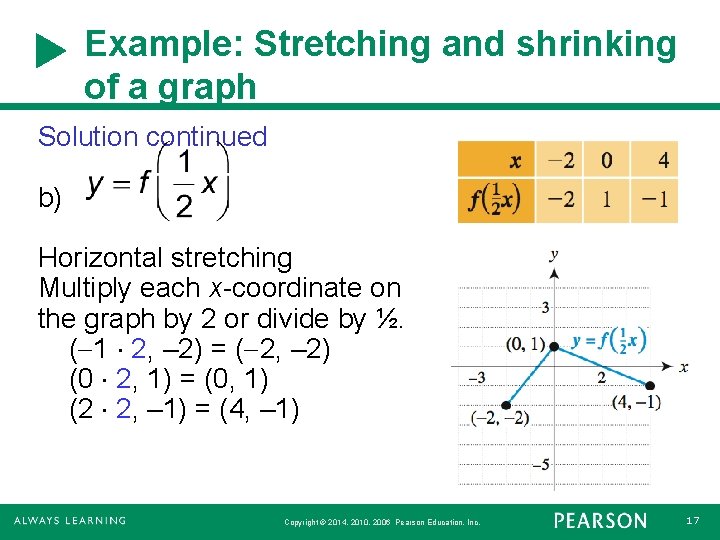
Example: Stretching and shrinking of a graph Solution continued b) Horizontal stretching Multiply each x-coordinate on the graph by 2 or divide by ½. ( 1 2, – 2) = ( 2, – 2) (0 2, 1) = (0, 1) (2 2, – 1) = (4, – 1) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 17

Reflection of Graphs Across the x- and y-Axes 1. The graph of y =

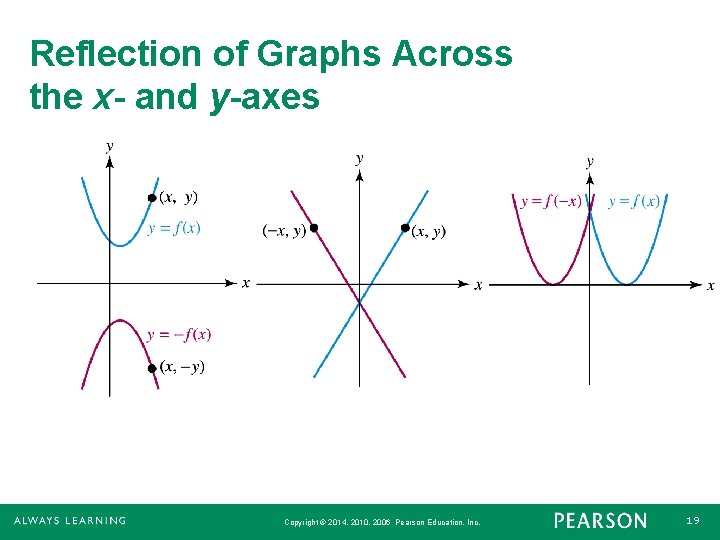
Reflection of Graphs Across the x- and y-Axes 1. The graph of y = –f(x) is a reflection of the graph of y = f(x) across the x-axis. 2. The graph of y = f(–x) is a reflection of the graph of y = f(x) across the y-axis. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 18

Reflection of Graphs Across the x- and y-axes Copyright © 2014, 2010, 2006 Pearson

Reflection of Graphs Across the x- and y-axes Copyright © 2014, 2010, 2006 Pearson Education, Inc. 19

Example: Reflecting graphs of functions For the representation of f, graph the reflection across

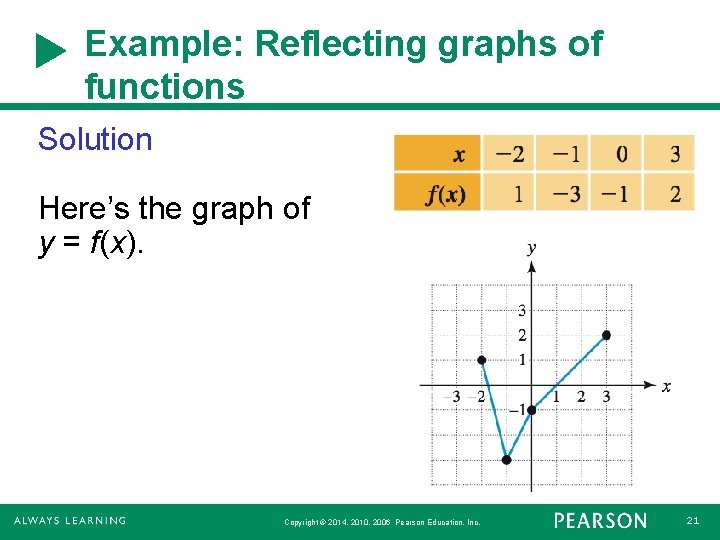
Example: Reflecting graphs of functions For the representation of f, graph the reflection across the x-axis and across the yaxis. The graph of f is a line graph determined by the table. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 20

Example: Reflecting graphs of functions Solution Here’s the graph of y = f(x). Copyright

Example: Reflecting graphs of functions Solution Here’s the graph of y = f(x). Copyright © 2014, 2010, 2006 Pearson Education, Inc. 21

Example: Reflecting graphs of functions Solution continued To graph the reflection of f across

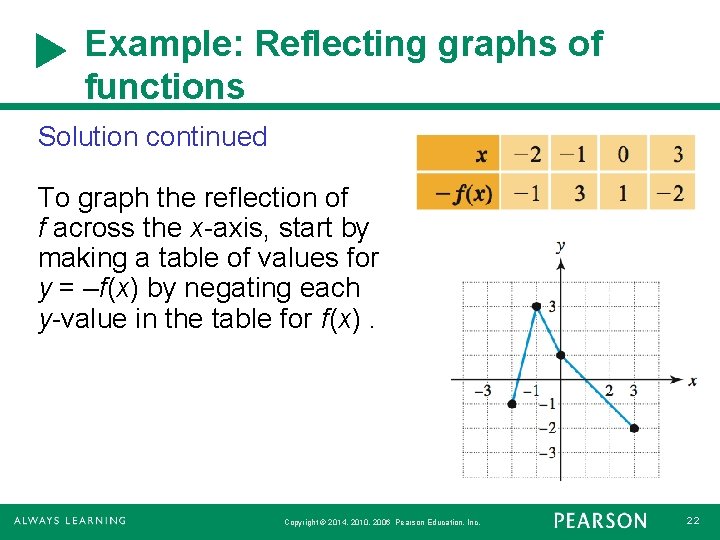
Example: Reflecting graphs of functions Solution continued To graph the reflection of f across the x-axis, start by making a table of values for y = –f(x) by negating each y-value in the table for f(x). Copyright © 2014, 2010, 2006 Pearson Education, Inc. 22

Example: Reflecting graphs of functions Solution continued To graph the reflection of f across

Example: Reflecting graphs of functions Solution continued To graph the reflection of f across the y-axis, start by making a table of values for y = f(–x) by negating each x-value in the table for f(x). Copyright © 2014, 2010, 2006 Pearson Education, Inc. 23

Combining Transformations of graphs can be combined to create new graphs. For example the

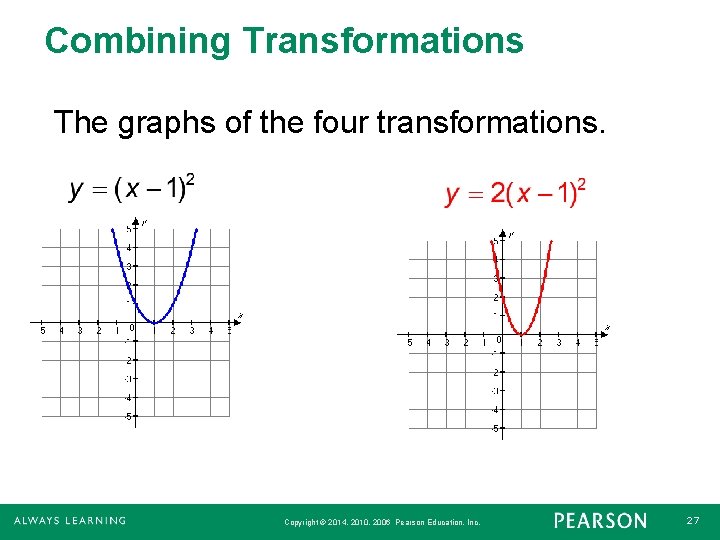
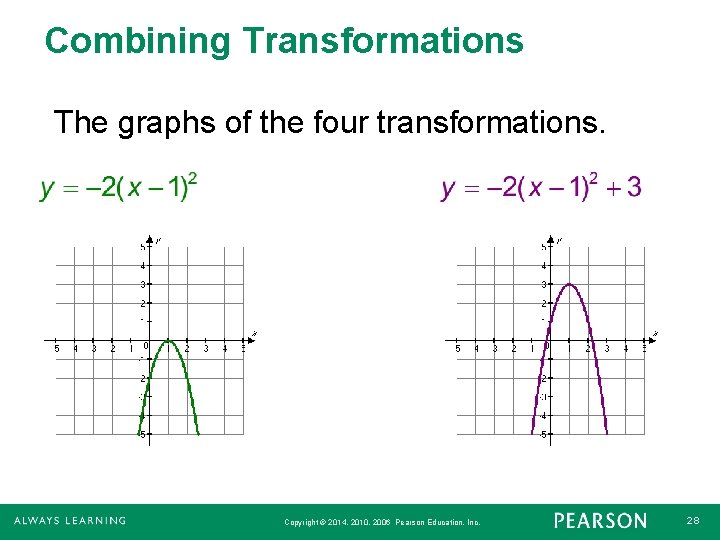
Combining Transformations of graphs can be combined to create new graphs. For example the graph of y = 2(x – 1)2 + 3 can be obtained by performing four transformations on the graph of y = x 2. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 24

Combining Transformations 1. Shift the graph 1 unit right: y = (x – 1)2

Combining Transformations 1. Shift the graph 1 unit right: y = (x – 1)2 2. Vertically stretch the graph by factor of 2: y = 2(x – 1)2 3. Reflect the graph across the x-axis: y = 2(x – 1)2 4. Shift the graph upward 3 units: y = 2(x – 1)2 + 3 Copyright © 2014, 2010, 2006 Pearson Education, Inc. 25

Combining Transformations continued Stretch vertically by a factor of 2 Shift to the left

Combining Transformations continued Stretch vertically by a factor of 2 Shift to the left 1 unit. y = 2(x – Reflect across the x-axis. 2 1) +3 Shift upward 3 units. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 26

Combining Transformations The graphs of the four transformations. Copyright © 2014, 2010, 2006 Pearson

Combining Transformations The graphs of the four transformations. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 27

Combining Transformations The graphs of the four transformations. Copyright © 2014, 2010, 2006 Pearson

Combining Transformations The graphs of the four transformations. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 28

Example: Combining transformations of graphs Describe how the graph of each equation can be

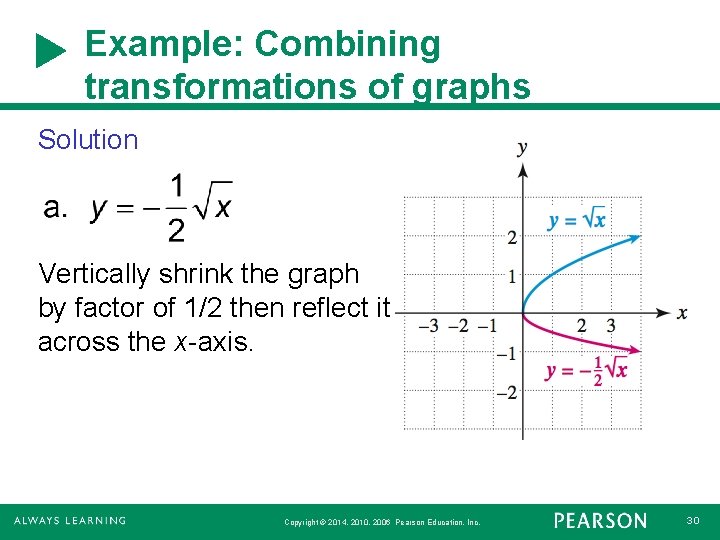
Example: Combining transformations of graphs Describe how the graph of each equation can be obtained by transforming the graph of Then graph the equation. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 29

Example: Combining transformations of graphs Solution Vertically shrink the graph by factor of 1/2

Example: Combining transformations of graphs Solution Vertically shrink the graph by factor of 1/2 then reflect it across the x-axis. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 30

Example: Combining transformations of graphs Solution continued Reflect it across the y-axis. Shift left

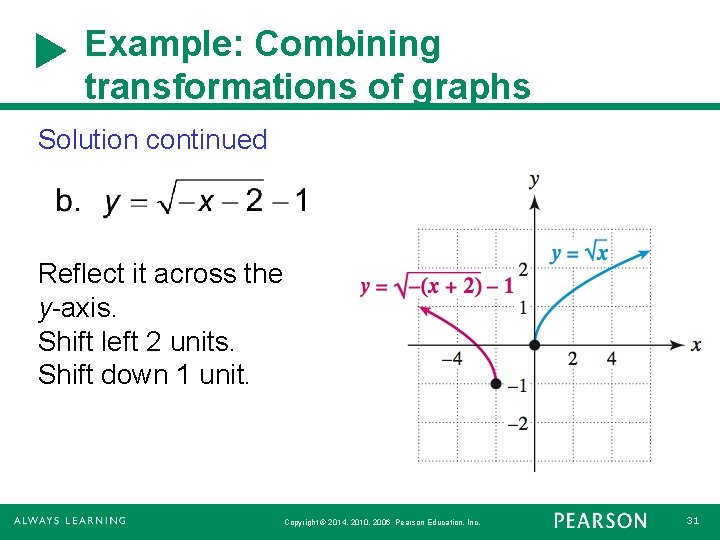
Example: Combining transformations of graphs Solution continued Reflect it across the y-axis. Shift left 2 units. Shift down 1 unit. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 31

Modeling Data with Transformations of the graph of y = x 2 can be

Modeling Data with Transformations of the graph of y = x 2 can be used to model some types of nonlinear data. By shifting, stretching, and shrinking this graph, we can transform it into a portion of a parabola that has the desired shape and location. In the next example we demonstrate this technique by modeling numbers of Wal-Mart employees. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 32

Example: Modeling data with a quadratic function The table lists numbers of Wal-Mart employees

Example: Modeling data with a quadratic function The table lists numbers of Wal-Mart employees in millions for selected years. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 33

Example: Modeling data with a quadratic function (a) Make a scatterplot of the data.

Example: Modeling data with a quadratic function (a) Make a scatterplot of the data. (b) Use transformations of graphs to determine f(x) =a(x – h)2 + k so that f(x) models the data. Graph y = f(x) together with the data. (c) Use f(x) to estimate the number of Wal-Mart employees in 2010. Compare it with the actual value of 2. 1 million employees. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 34

Example: Modeling data with a quadratic function Solution Here’s a calculator display of a

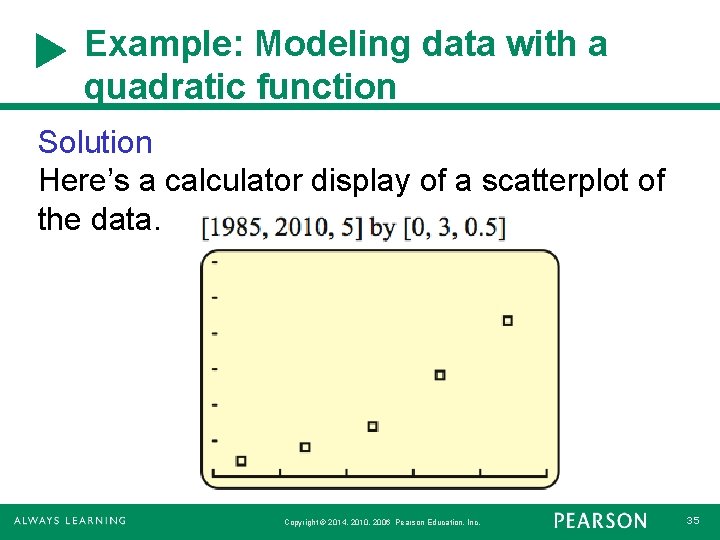
Example: Modeling data with a quadratic function Solution Here’s a calculator display of a scatterplot of the data. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 35

Example: Modeling data with a quadratic function Solution continued It’s a parabola opening up

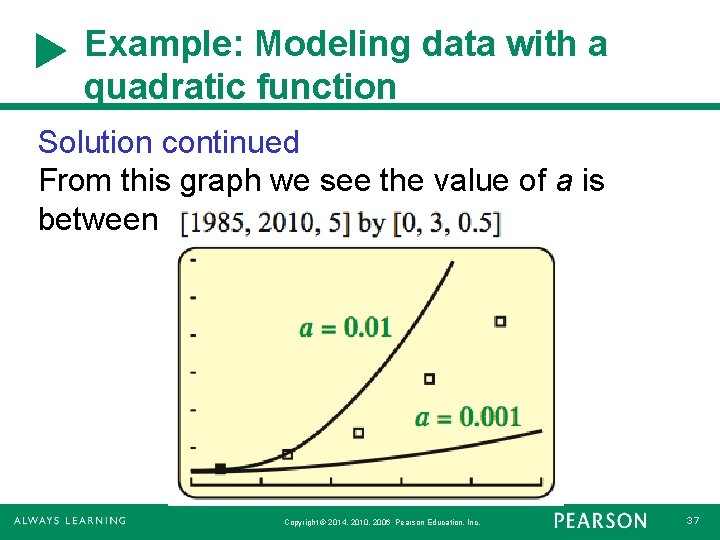
Example: Modeling data with a quadratic function Solution continued It’s a parabola opening up so a > 0. Vertex (minimum number of employees) could be (1987, 0. 20): translate graph right 1987 units and up 0. 20 unit. f(x) = a(x – 1987) + 0. 20 To determine a, graph the data for different values of a: First graph a = 0. 001 and a = 0. 01. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 36

Example: Modeling data with a quadratic function Solution continued From this graph we see

Example: Modeling data with a quadratic function Solution continued From this graph we see the value of a is between 0. 001 and 0. 01. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 37

Example: Modeling data with a quadratic function Solution continued Experimenting yields a value of

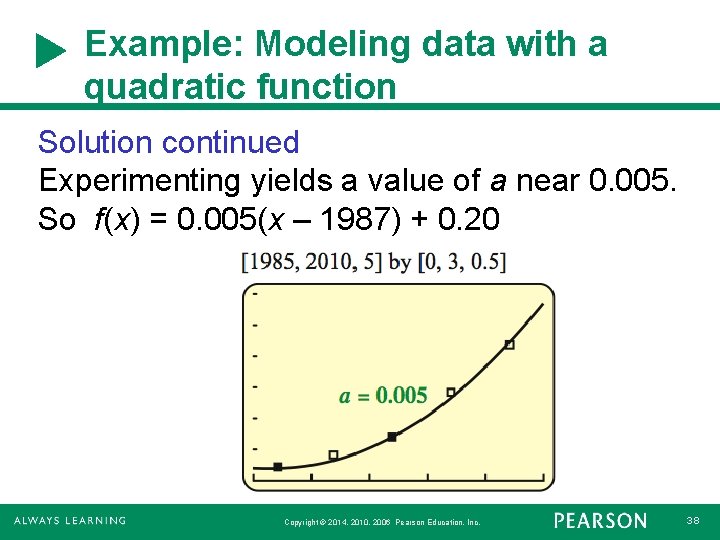
Example: Modeling data with a quadratic function Solution continued Experimenting yields a value of a near 0. 005. So f(x) = 0. 005(x – 1987) + 0. 20 Copyright © 2014, 2010, 2006 Pearson Education, Inc. 38