Chapter 3 Pulse Code Modulation Pulse Code Modulation

Chapter 3: Pulse Code Modulation Ø Ø Ø Pulse Code Modulation Quantizing Encoding Analogue to Digital Conversion Bandwidth of PCM Signals Huseyin Bilgekul Eeng 360 Communication Systems I Department of Electrical and Electronic Engineering Eastern Mediterranean University 1

PULSE CODE MODULATION (PCM) Ø DEFINITION: Pulse code modulation (PCM) is essentially analog-to-digital conversion of a special type where the information contained in the instantaneous samples of an analog signal is represented by digital words in a serial bit stream. Ø The advantages of PCM are: • Relatively inexpensive digital circuitry may be used extensively. • PCM signals derived from all types of analog sources may be merged with data signals and transmitted over a common high-speed digital communication system. • In long-distance digital telephone systems requiring repeaters, a clean PCM waveform can be regenerated at the output of each repeater, where the input consists of a noisy PCM waveform. • The noise performance of a digital system can be superior to that of an analog system. • The probability of error for the system output can be reduced even further by the use of appropriate coding techniques. 2

Sampling, Quantizing, and Encoding Ø The PCM signal is generated by carrying out three basic operations: 1. Sampling 2. Quantizing 3. Encoding 1. 2. Sampling operation generates a flat-top PAM signal. Quantizing operation approximates the analog values by using a finite number of levels. This operation is considered in 3 steps a) Uniform Quantizer b) Quantization Error c) Quantized PAM signal output 3. PCM signal is obtained from the quantized PAM signal by encoding each quantized sample value into a digital word. 3

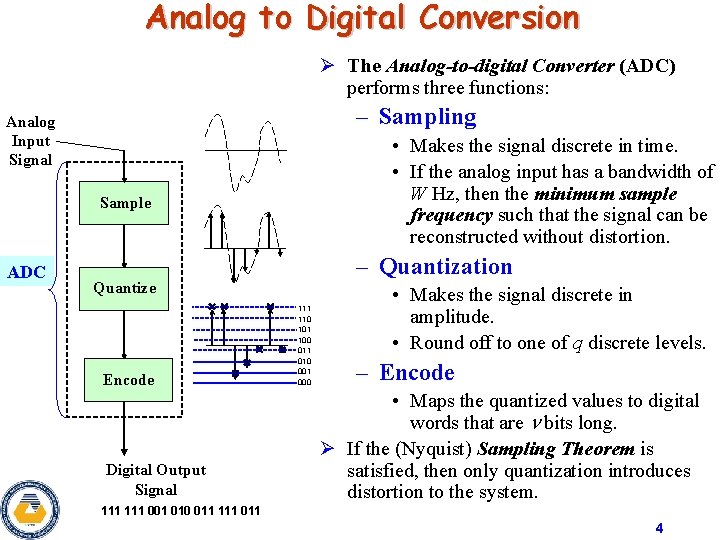
Analog to Digital Conversion Ø The Analog-to-digital Converter (ADC) performs three functions: – Sampling Analog Input Signal • Makes the signal discrete in time. • If the analog input has a bandwidth of W Hz, then the minimum sample frequency such that the signal can be reconstructed without distortion. Sample ADC – Quantization Quantize Encode Digital Output Signal 111 110 101 100 011 010 001 000 • Makes the signal discrete in amplitude. • Round off to one of q discrete levels. – Encode • Maps the quantized values to digital words that are bits long. Ø If the (Nyquist) Sampling Theorem is satisfied, then only quantization introduces distortion to the system. 111 001 010 011 111 011 4

Quantization Ø The output of a sampler is still continuous in amplitude. – Each sample can take on any value e. g. 3. 752, 0. 001, etc. – The number of possible values is infinite. Ø To transmit as a digital signal we must restrict the number of possible values. Ø Quantization is the process of “rounding off” a sample according to some rule. – E. g. suppose we must round to the nearest tenth, then: 3. 752 --> 3. 8 0. 001 --> 0 5

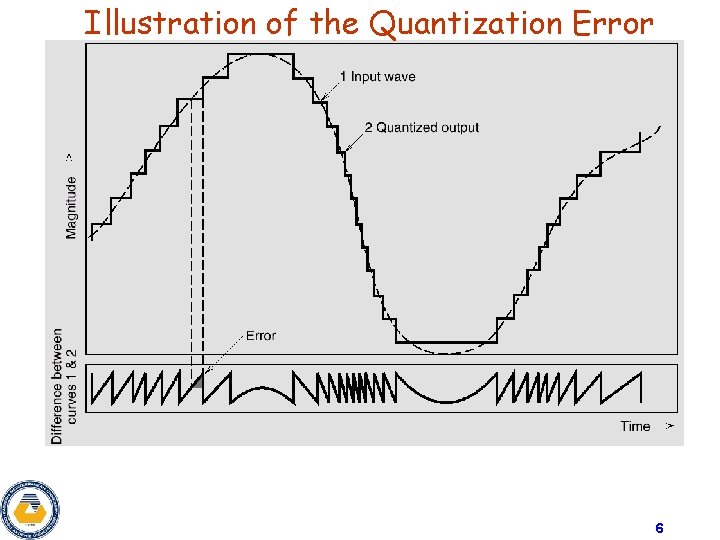
Illustration of the Quantization Error 6

PCM TV transmission: (a) 5 -bit resolution; (b) 8 -bit resolution. 7

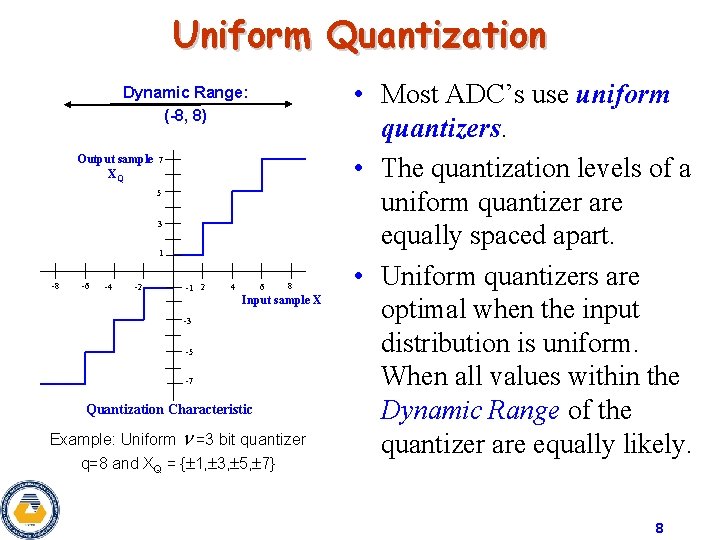
Uniform Quantization Dynamic Range: (-8, 8) Output sample XQ 7 5 3 1 -8 -6 -4 -2 -1 2 4 6 8 Input sample X -3 -5 -7 Quantization Characteristic Example: Uniform =3 bit quantizer q=8 and XQ = { 1, 3, 5, 7} • Most ADC’s use uniform quantizers. • The quantization levels of a uniform quantizer are equally spaced apart. • Uniform quantizers are optimal when the input distribution is uniform. When all values within the Dynamic Range of the quantizer are equally likely. 8

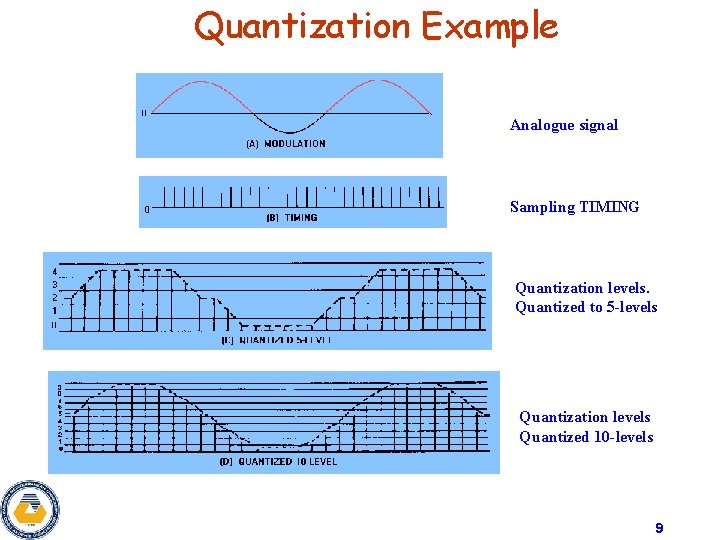
Quantization Example Analogue signal Sampling TIMING Quantization levels. Quantized to 5 -levels Quantization levels Quantized 10 -levels 9

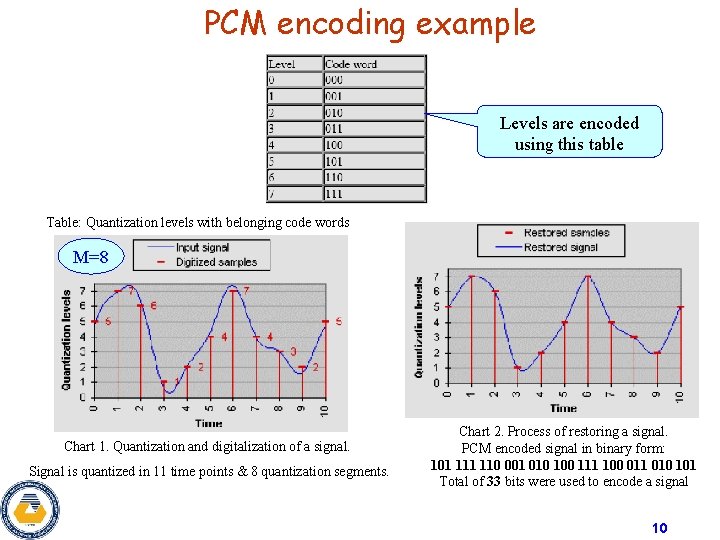
PCM encoding example Levels are encoded using this table Table: Quantization levels with belonging code words M=8 Chart 1. Quantization and digitalization of a signal. Signal is quantized in 11 time points & 8 quantization segments. Chart 2. Process of restoring a signal. PCM encoded signal in binary form: 101 110 001 010 100 111 100 011 010 101 Total of 33 bits were used to encode a signal 10

Encoding • The output of the quantizer is one of M possible signal levels. – If we want to use a binary transmission system, then we need to map each quantized sample into an n bit binary word. • Encoding is the process of representing each quantized sample by an bit code word. – The mapping is one-to-one so there is no distortion introduced by encoding. – Some mappings are better than others. • A Gray code gives the best end-to-end performance. • The weakness of Gray codes is poor performance when the sign bit (MSB) is received in error. 11

Gray Codes • With gray codes adjacent samples differ only in one bit position. • Example (3 bit quantization): XQ +7 +5 +3 +1 -1 -3 -5 -7 Natural coding 111 110 101 100 011 010 001 000 Gray Coding 110 111 100 001 010 • With this gray code, a single bit error will result in an amplitude error of only 2. – Unless the MSB is in error. 12

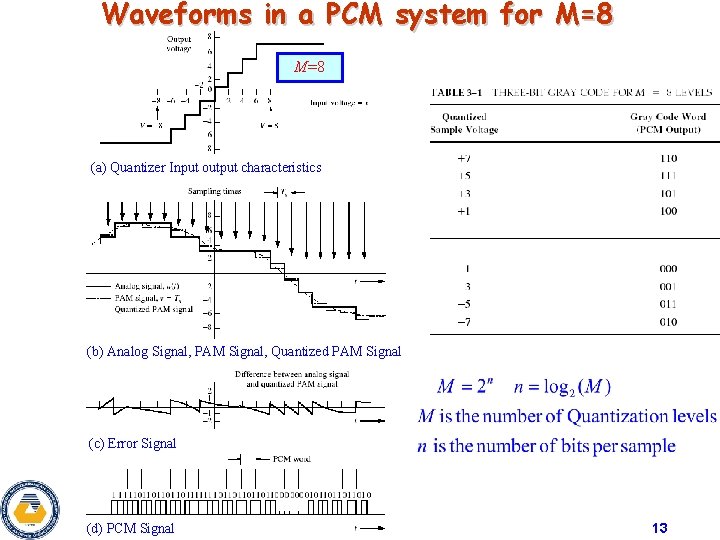
Waveforms in a PCM system for M=8 (a) Quantizer Input output characteristics (b) Analog Signal, PAM Signal, Quantized PAM Signal (c) Error Signal (d) PCM Signal 13

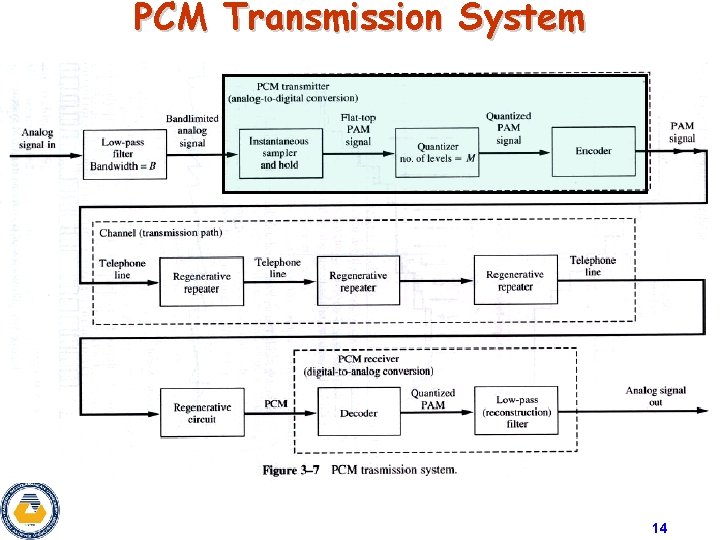
PCM Transmission System 14

Practical PCM Circuits • Three popular techniques are used to implement the analog-to-digital converter (ADC) encoding operation: 1. 2. 3. • • The counting or ramp, ( Maxim ICL 7126 ADC) Serial or successive approximation, (AD 570) Parallel or flash encoders. ( CA 3318) The objective of these circuits is to generate the PCM word. Parallel digital output obtained (from one of the above techniques) needs to be serialized before sending over a 2 -wire channel This is accomplished by parallel-to-serial converters [Serial Input-Output (SIO) chip] UART, USRT and USART are examples for SIO’s 15

Bandwidth of PCM Signals • • The spectrum of the PCM signal is not directly related to the spectrum of the input signal. The bandwidth of (serial) binary PCM waveforms depends on the bit rate R and the waveform pulse shape used to represent the data. The Bit Rate R is R=nfs Where n is the number of bits in the PCM word (M=2 n) and fs is the sampling rate. For no aliasing case (fs≥ 2 B), the MINIMUM Bandwidth of PCM Bpcm(Min) is: Bpcm(Min) = R/2 = nfs//2 The Minimum Bandwidth of nfs//2 is obtained only when sin(x)/x pulse is used to generate the PCM waveform. • For PCM waveform generated by rectangular pulses, the First-null Bandwidth is: Bpcm = R = nfs 16