Chapter 3 Projectile Motion Part 1 Math Rev

Chapter 3 Projectile Motion Part 1 – Math Rev; intro to Trig and Vectors

Math Review or Introduction Right triangles and trig

Review… n What is a scalar quantity? – a quantity with magnitude

What is magnitude? n How much of something you have; an amount only; a number

What is a vector quantity? n A quantity that has both magnitude and direction

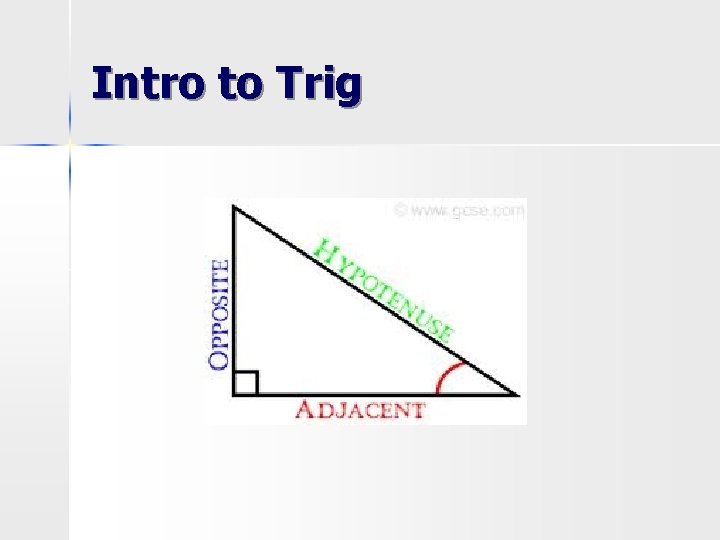
Right Triangles One side has a right angle (90°) n The other two angles must add up to 90 n Side opposite the right angle is the hypotenuse n

Right Triangles con’t n Pythagorean Theorem – know 2 sides; find third side

Examples 10 ? 15

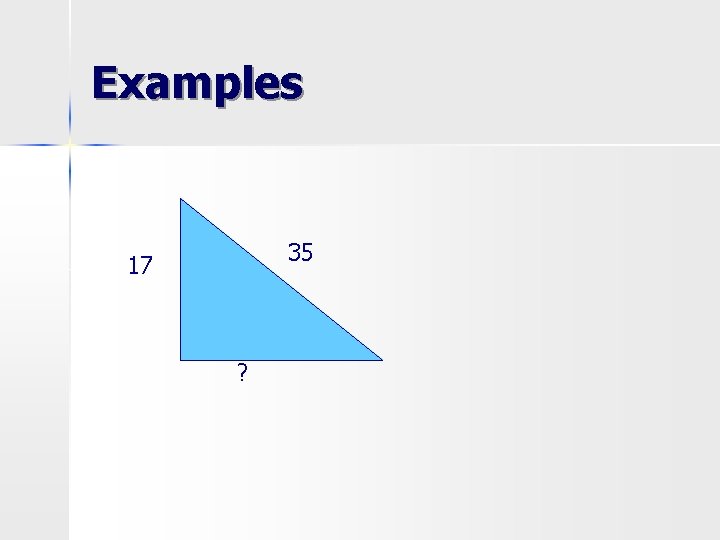
Examples 35 17 ?

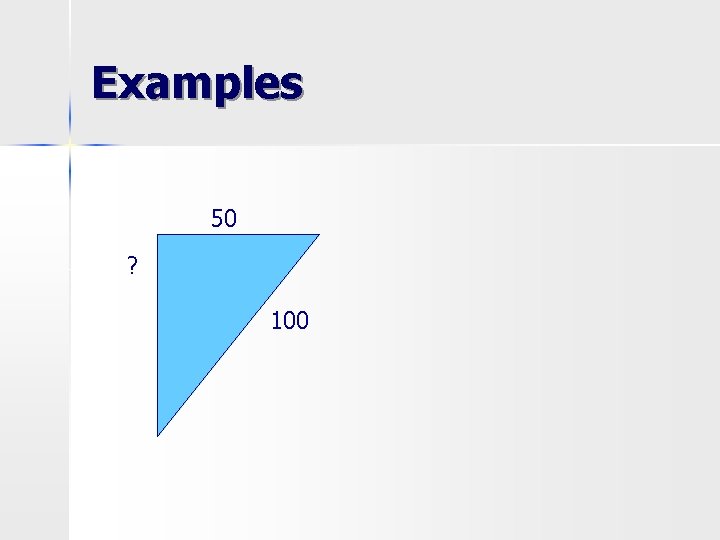
Examples 50 ? 100

Intro to Trig

Which side is the h, o and a?

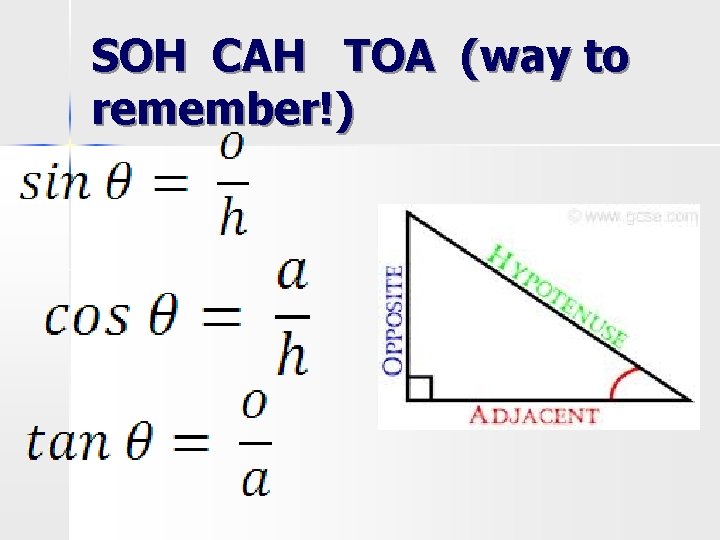
3 Trig functions to find a side when given an angle NOTE: θ IS THE ANGLE IN DEGREES!

SOH CAH TOA (way to remember!)

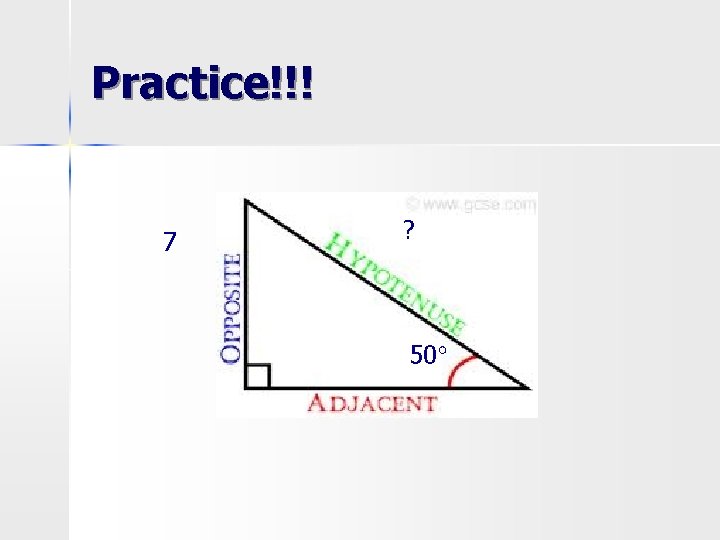
Practice!!! 7 ? 50°

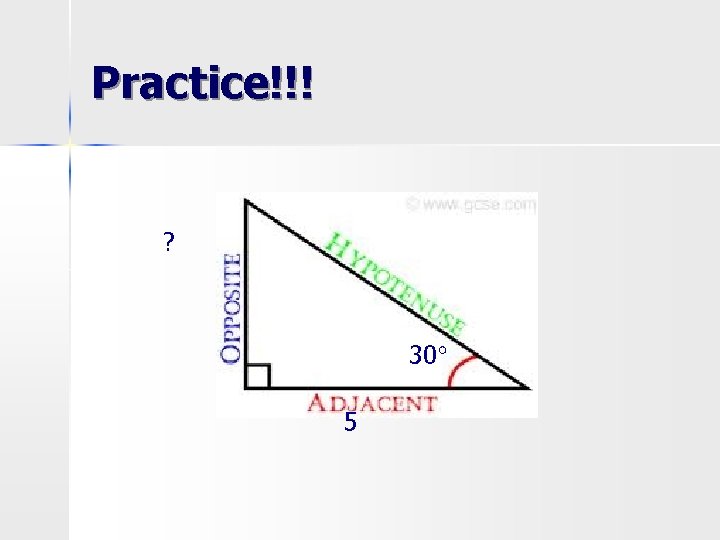
Practice!!! ? 30° 5

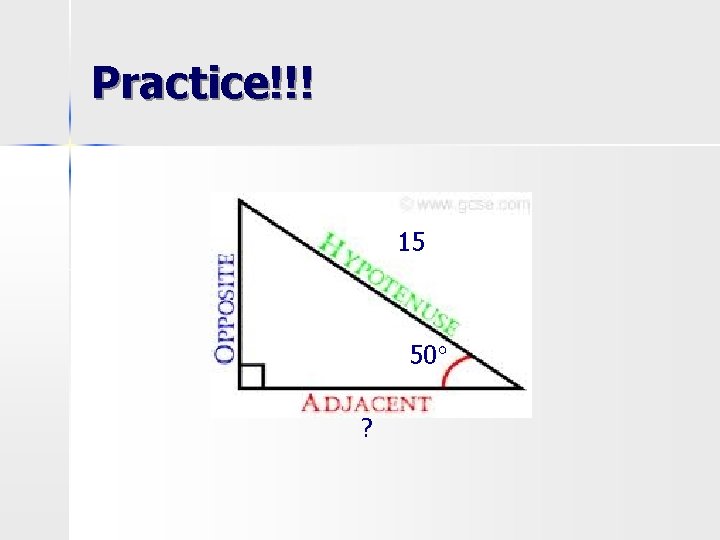
Practice!!! 15 50° ?

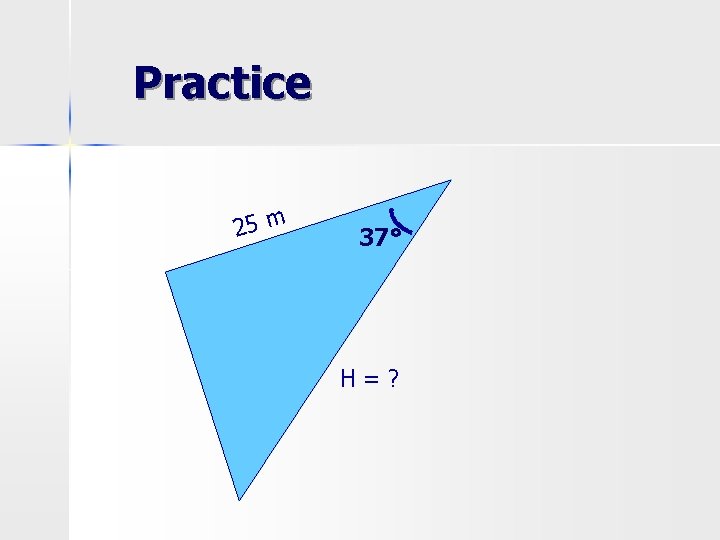
Practice 25 m 37° H=?

Trig con’t (finding angles)

Finding the angle: use the inverse function! (2 nd key and then the function)

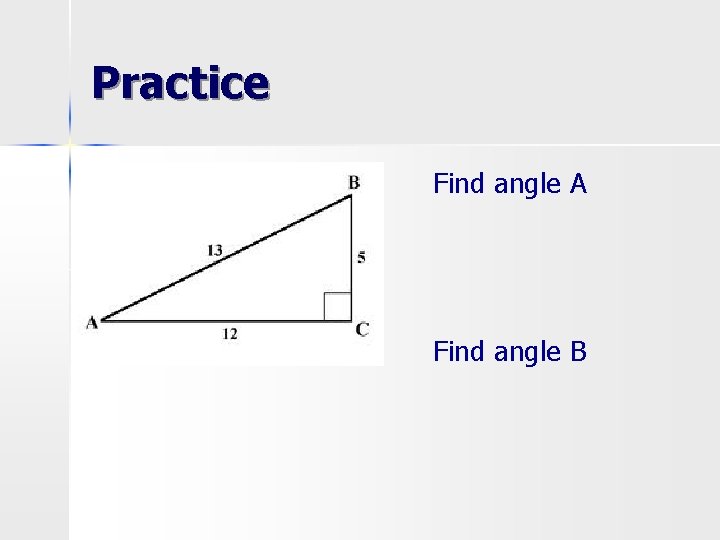
Practice Find angle A Find angle B

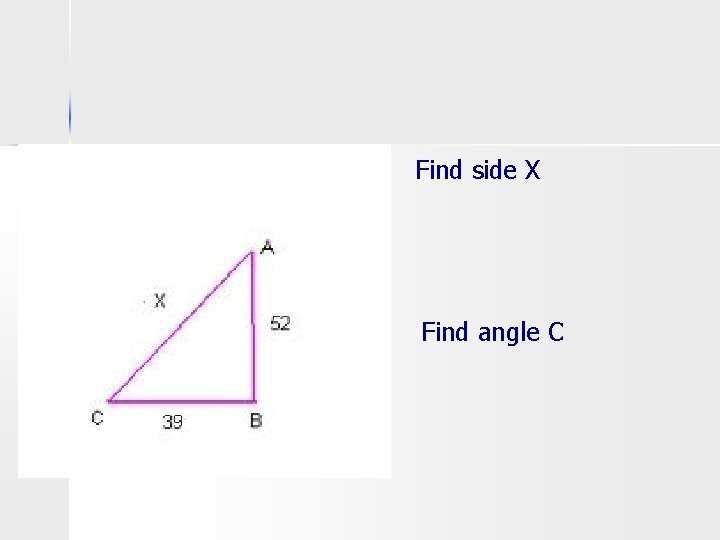
Find side X Find angle C

What a vector can represent: n A drawn vector can be used to represent distance, velocity, acceleration or a force

Drawing Vectors… n Length of the vector is the magnitude – We use scaled drawings: like a map n Angle and arrow indicate direction – Direction can be in degrees, NSEW, both degrees and NSEW, up or down, left or right

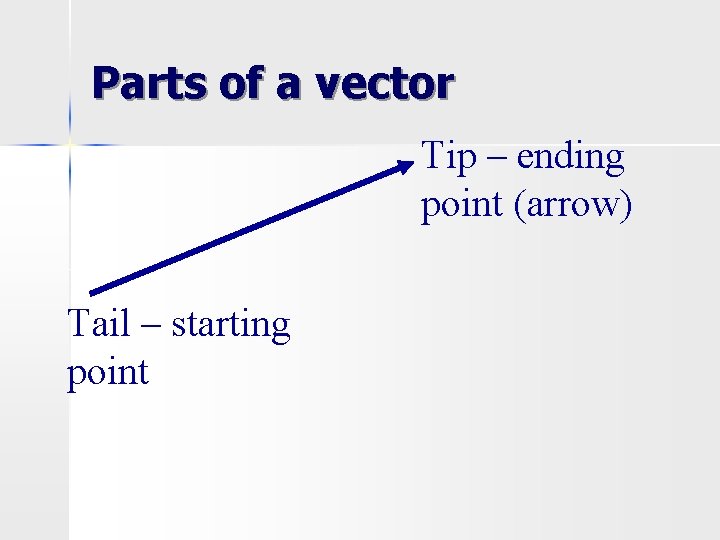
Parts of a vector Tip – ending point (arrow) Tail – starting point

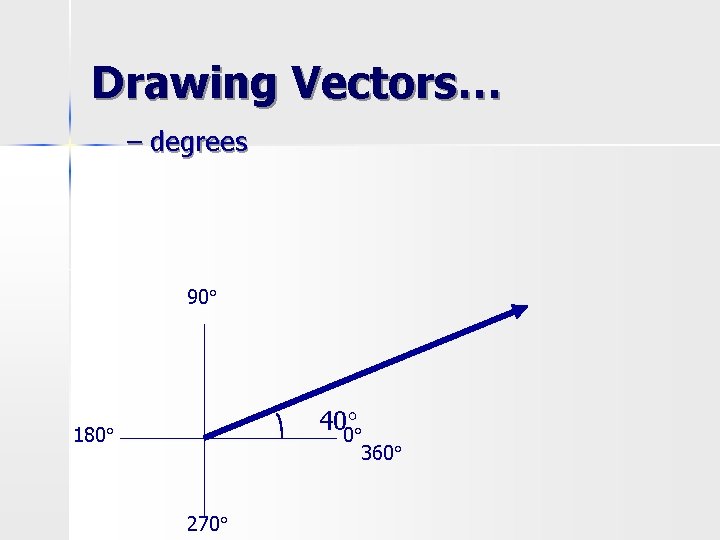
Drawing Vectors… – degrees 90° 40° 0° 180° 270° 360°

Drawing Vectors… – degrees 250°

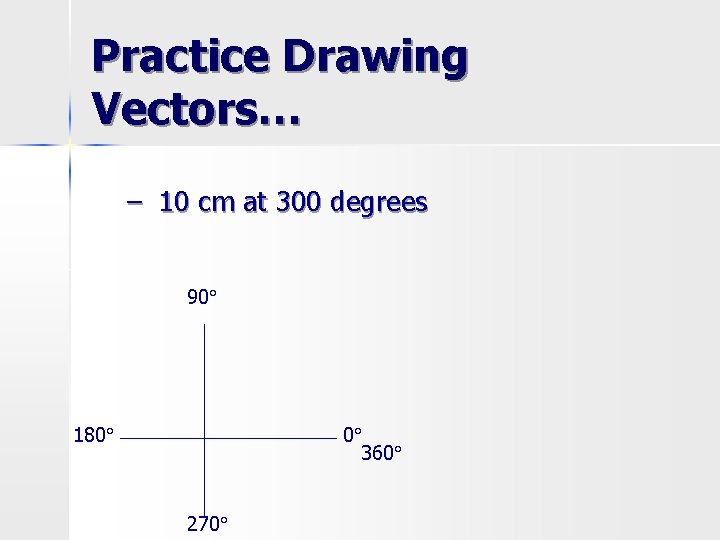
Practice Drawing Vectors… – 10 cm at 300 degrees 90° 180° 0° 270° 360°

Drawing Vectors… – Degrees and N, S, E and W – Example: 3 cm at 70° toward S from directly W (S of W) Put protractor on W and go 70° S 70°

1. Practice – draw a 6 cm vector at 40° towards North from directly E (N of E) 2. Practice – draw a 4 cm vector at 60° towards E from directly S (E of S)

How would you draw 340° ? How can we rename this angle to fit our standard form (note: angle between 0 and 90) ____° towards _____directly from ______? n

Shortening the direction n _____ of ____ Axis you start your measurement from…line up 0 degrees at this axis

Rewrite in shortened form…. – draw a 5 cm vector at 30° towards North from directly E

Drawing Vectors… – Example: 3 cm at 70° toward S from directly W – Becomes 3 cm at ______________ 70°

Shortened direction? – Practice – draw a 7 cm vector at 60° towards E from directly S

Adding Vectors n Resultant –the _____ of two or more vectors

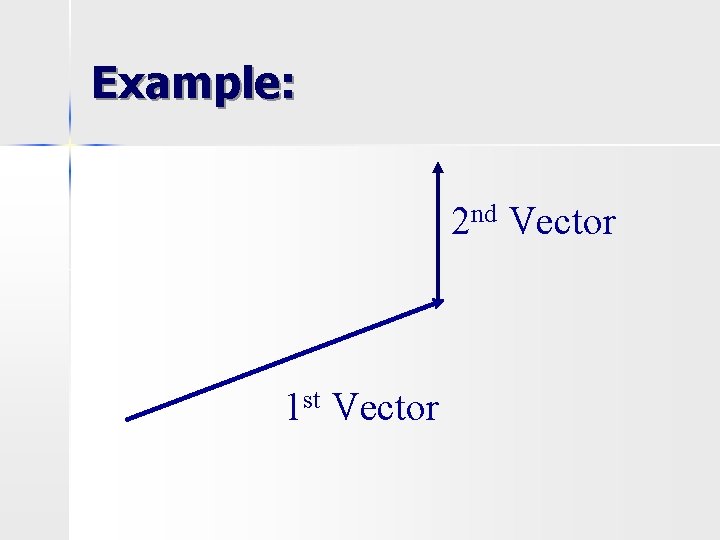
2 main methods of adding vectors 1. Head to tail method (aka tip to tail) ü Draw first vector ü Start next vector where the last one ended (so its tail is connected to the previous vectors tip)

Example: 2 nd Vector 1 st Vector

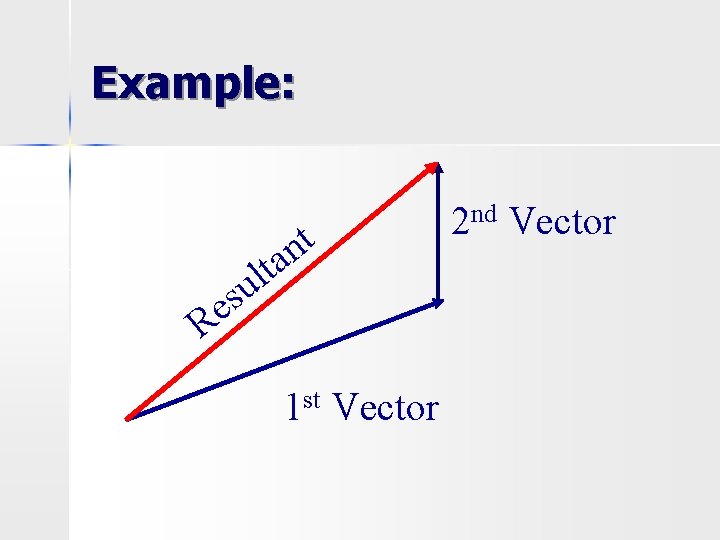
Drawing Resultant n Start where the first vector starts and end where the last vector ends

Example: t n a t ul s e R 1 st Vector 2 nd Vector

Practice Tip-to-Tail Method

Place the following quantities in the appropriate column…are they a scalar or vector quantity? Time n Acceleration n Distance n Velocity n Displacement n Speed n

2 nd Method of adding vectors n Tail-to-tail method: –Also known as the Parallelogram Method üDraw the first vector üDraw the second vector starting from the tail of the first vector

Drawing the Resultant n Form a parallelogram from the two vectors – Do this by drawing lines that are parallel to the two vectors n Resultant starts where the two vectors start and ends in the opposite corner

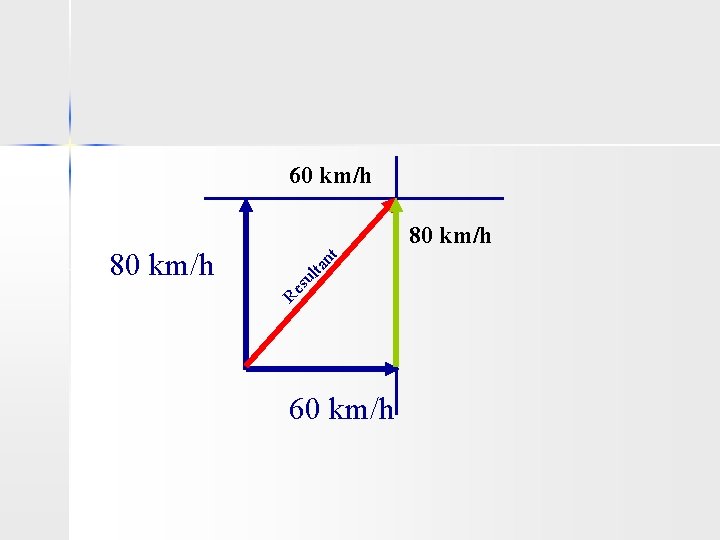
Example: Crosswind n An airplane is flying 80 km/h north is caught in a strong crosswind of 60 km/h blowing from west to east. Will the airplane fly faster or slower than 80 km/h?

60 km/h nt lta su Re 80 km/h 60 km/h

n Then we can use the Pythagorean Theorem to find the hypotenuse which is our resultant – A 2 + B 2 = C 2 C = √(A 2 + B 2)

Graphically vs Mathematically adding vectors Graphically finding the information for vectors is using only a drawing and the measurements n Mathematically is actually adding the numbers n In most cases we will use both methods to double check our answers n

Problems Involving Vectors

PE 1 -6 Remember to set a scale! n Be careful with directions! THINK through EACH problem n Include magnitude and direction in your final answer n

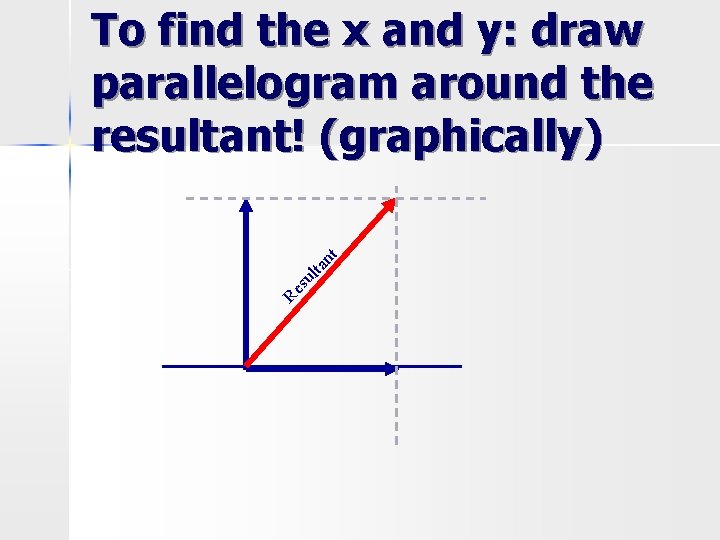
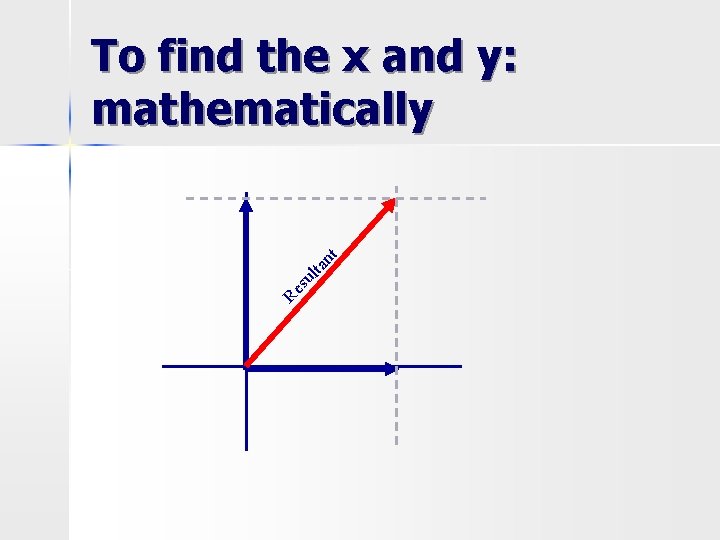
Vector Resolution or resolving the vector – Breaking the resultant vector into its two vector components n HINT: you are given only ONE vector! n

Parts of a vector: Vector Components Component – the two vectors at right angles with one another that are added to form the resultant (the single vector) n (the x and y vectors aka the horizontal and vertical components) n

Re su lta nt To find the x and y: draw parallelogram around the resultant! (graphically)

Re su lta nt To find the x and y: mathematically