Chapter 3 Programming with MATLAB Numerical Solution Newtons

Chapter 3 Programming with MATLAB

Numerical Solution Ø Newton’s Second Law Ø Euler’s method Ø To obtain good accuracy, it is necessary to use many small steps Ø Extremely laborious and time-consuming to implement by hand

M-Files: Scripts and Functions n n n You can create and save code in text files using MATLAB Editor/Debugger or other text editors (called m-files since the ending must be. m) M-file is an ASCII text file similar to FORTRAN or C source codes ( computer programs) A script can be executed by typing the file name, or using the “run” command Difference between scripts and functions Scripts share variables with the main workspace Functions do not

Script Files Ø Script file – a series of MATLAB commands saved on a file, can be executed by q typing the file name in the Command Window q invoking the menu selections in the Edit Window: Debug, Run Ø Create a script file using menu selection: File, New, M-file

Script File – Bungee Jumper n n Compute the velocity of a free-falling bungee jumper at a specific time Open the editor with: File, New, M-file g = 9. 81; m = 68. 1 ; t = 20; cd = 0. 25; v = sqrt(g*m/cd) * tanh(sqrt(g*cd/m)*t) n n Save the file as bungee_jumper. m Type bungee_jumper in command window » bungee_jumper v = 51. 6416 Type the name of the script file

Function File n n n Function file: M-file that starts with the word function Function can accept input arguments and return outputs Analogous to user-defined functions in programming languages such as Fortran, C, … Save the function file as function_name. m User help function in command window for additional information

Functions n n One output variable function y = function_name(input arguments) More than one output variables function [y, z] = function_name(input arguments) Examples: function y = my_func (x) y = x^3 + 3*x^2 -5 * x +2 ; function area = integral (f, a, b) ya = feval (f, a); yb = feval(f, b); area = (b-a)*(ya+yb)/2;

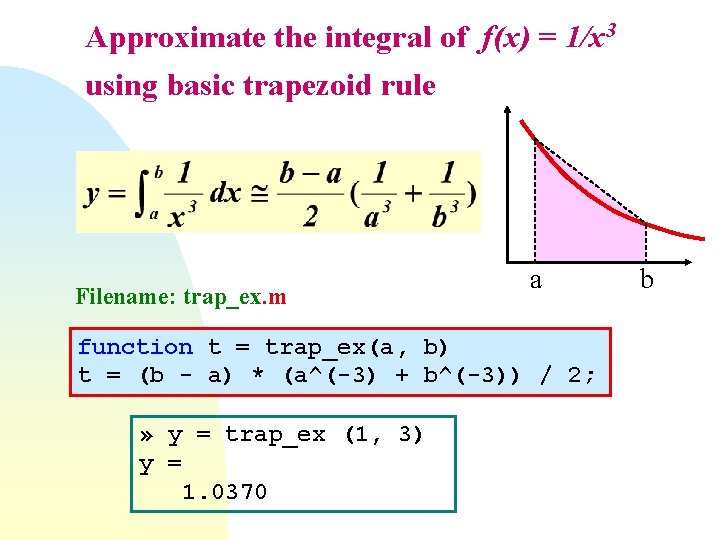
Approximate the integral of f(x) = 1/x 3 using basic trapezoid rule Filename: trap_ex. m a function t = trap_ex(a, b) t = (b - a) * (a^(-3) + b^(-3)) / 2; » y = trap_ex (1, 3) y = 1. 0370 b

Script File for Integral f(x) area a 1. Save integral (f, a, b) in script file integral. m 2. Save function my_func(x) in script my_func. m 3. Run script file >> area = integral(‘my_func’, 1, 10) >> area = integral(‘my_func’, 3, 6) b x

feval - evaluate function specified by string my_func. m function y = my_func(x) % function 1/x^3 y = x. ^(-3); function q = basic_trap(f, a, b) % basic trapezoid rule basic_trap. m ya = feval(f, a); yb = feval(f, b); q = (b - a)* (ya + yb)/2; » y = basic_trap ('my_func', 1, 3) y = 1. 0370

Composite Trapezoid Rule Filename: comp_trap. m function I = Trap(f, a, b, n) % find the integral of f using % composite trapezoid rule h=(b - a)/n; f S = feval(f, a); for i = 1 : n-1 x(i) = a + h*i; S = S + 2*feval(f, x(i)); end S = S + feval(f, b); I =h*S/2; a b x

Composite Trapezoid Rule » I=comp_trap('my_func', 1, 3, 1) I = 1. 0370 » I=comp_trap('my_func', 1, 3, 2) I = 0. 6435 » I=comp_trap('my_func', 1, 3, 4) I = 0. 5019 » I=comp_trap('my_func', 1, 3, 8) I = 0. 4596 » I=comp_trap('my_func', 1, 3, 16) I = 0. 4483 » I=comp_trap('my_func', 1, 3, 100) I = 0. 4445 » I=comp_trap('my_func', 1, 3, 500) I = 0. 4444 » I=comp_trap('my_func', 1, 3, 1000) I = 0. 4444 one segment two segments four segments eight segments 16 segments 100 segments 500 segments 1000 segments

Function File – Bungee Jumper n Create a function file freefallvel. m function velocity = freefallvel(m, cd, t) % freefallvel(m, cd, t) computes the free-fall velocity (m/s) % of an object with second-order drag % input: % m = mass (kg) % cd = second-order drag coefficient (kg/m) % t = time (sec) % output: % velocity = downward velocity (m/s) g = 9. 81; % acceleration of gravity velocity = sqrt(g*m/cd) * tanh(sqrt(g*cd/m)*t);

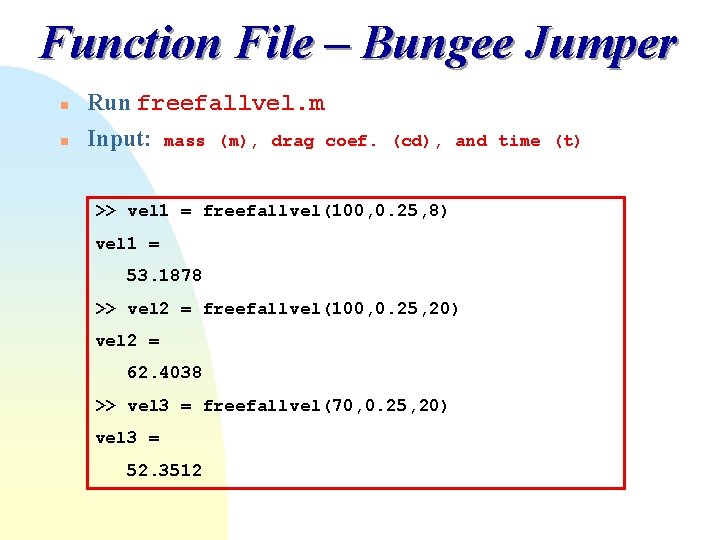
Function File – Bungee Jumper n Run freefallvel. m n Input: mass (m), drag coef. (cd), and time (t) >> vel 1 = freefallvel(100, 0. 25, 8) vel 1 = 53. 1878 >> vel 2 = freefallvel(100, 0. 25, 20) vel 2 = 62. 4038 >> vel 3 = freefallvel(70, 0. 25, 20) vel 3 = 52. 3512

Function File n n To invoke the help comments Type help freefallvel >> help freefallvel(m, cd, t) computes the free-fall velocity (m/s) of an object with second-order drag input: m = mass (kg) cd = second-order drag coefficient (kg/m) t = time (sec) output: velocity = downward velocity (m/s)

Function M-Files n n Function M-file can return more than one result Example – mean and standard deviation of a vector function [mean, stdev] = stats(x) % calculate the mean and standard deviation of a vector x n = length(x); mean = sum(x)/n; stdev = sqrt(sum((x-mean). ^2/(n-1))); >> x=[1. 5 3. 7 5. 4 2. 6 0. 9 2. 8 5. 2 4. 9 6. 3 3. 5]; >> [m, s] = stats(x) m = 3. 6800 s = 1. 7662 n Textbook refers function M-files as simply M-files

Data Files n MAT Files -- memory efficient binary format -- preferable for internal use by MATLAB program n ASCII files -- in ASCII characters -- useful if the data is to be shared (imported or exported to other programs)

MATLAB Input To read files in n n if the file is an ascii table, use “load” if the file is ascii but not a table, file I/O needs “fopen” and “fclose” Reading in data from file using fopen depends on type of data (binary or text) Default data type is “binary”

Save Files n n n 8 -digit text format (variable list) save <fname> <vlist> - ascii 16 -digit text format save <fname> <vlist> - double Delimit elements with tabs save <fname> <vlist> - double - tabs Example: Vel = [1 3 5; -6 2 -3] save velocity. dat Vel -ascii 1. 0000000 e+000 3. 0000000 e+000 5. 0000000 e+000 -6. 0000000 e+000 2. 0000000 e+000 -3. 0000000 e+000

Load Files n Read velocity into a matrix “velocity. dat” >> load velocity. dat >> velocity = 1 3 5 -6 2 -3 1. 0000000 e+000 3. 0000000 e+000 5. 0000000 e+000 -6. 0000000 e+000 2. 0000000 e+000 -3. 0000000 e+000

Load Files n Create an ASCII file temperature. dat % Time 0. 0 0. 5 1. 0 1. 5 2. 0 2. 5 n Temperature 75. 0 73. 2 72. 6 74. 8 79. 3 83. 2 read “Time” and “Temperature” from temp. dat >> load temperature. dat >> temperature Note: temperature is a 6 2 matrix

MATLAB Output Matlab automatically prints the results of any calculation (unless suppressed by semicolon ; ) Use “disp” to print out text to screen disp (x. *y) disp (´Temperature =´) sprintf - display combination Make a string to print to the screen output = sprintf(‘Pi is equal to %f ’, pi)

Formatted Output fprintf (format-string, var, …. ) %[flags] [width] [. precision] type Examples of “type” fields %d display in integer format %e display in lowercase exponential notation %E display in uppercase exponential notation %f display in fixed point or decimal notation %g display using %e or %f, depending on which is shorter %% display “%”

Numeric Display Format x = [5 -2 3 0 1 -2]; format + x = [+ + + ] (+/ sign only)

fprintf( ) of Scalar temp = 98. 6; fprintf(‘The temperature is %8. 1 f degrees F. n’, temp); The temperature is 98. 6 degrees F. fprintf(‘The temperature is %08. 2 f degrees F. n’, temp); The temperature is 00098. 60 degrees F. fprintf(‘The temperature is %8. 3 e degrees F. n’, temp); The temperature is 9. 860 e+001 degrees F.

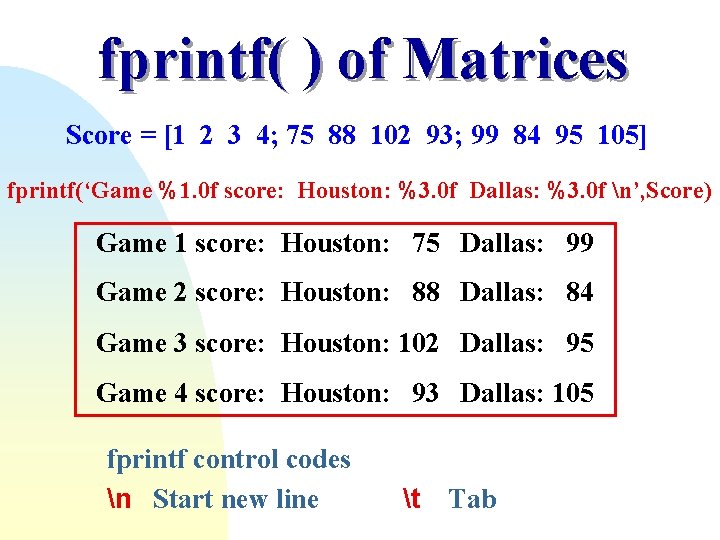
fprintf( ) of Matrices Score = [1 2 3 4; 75 88 102 93; 99 84 95 105] fprintf(‘Game %1. 0 f score: Houston: %3. 0 f Dallas: %3. 0 f n’, Score) Game 1 score: Houston: 75 Dallas: 99 Game 2 score: Houston: 88 Dallas: 84 Game 3 score: Houston: 102 Dallas: 95 Game 4 score: Houston: 93 Dallas: 105 fprintf control codes n Start new line t Tab

Interactive input Function Ø The input function allows you to prompt the user for values directly from the command window n = input(‘promptstring’) Ø Enter either “value” or “stream” function [name, sid, phone, email] = register name = input('Enter your name: ', 's'); sid = input('Enter your student ID: '); value phone = input('Enter your Telphone number: ', 's'); email = input('Enter your Email address: ', 's'); string

Interactive input Function >> [name, sid, phone, email] = register Enter your name: John Doe Enter your student ID: 12345678 Enter your Telphone number: 987 -6543 Enter your Email address: John. Doe@tamu. edu name = John Doe sid = 12345678 phone = 987 -6543 email = John. Doe@tamu. edu

Interactive M-File Ø An interactive M-file for free-falling bungee jumper Ø Use input and disp functions for input/output function velocity = freefallinteract % freefallinteract() % compute the free-fall velocity of a bungee jumper % input: interactive from command window % output: ve; ocity = downward velocity (m/s) g=9. 81; % acceleration of gravity m = input('Mass (kg): '); cd = input('Drag coefficient (kg/m): '); t = input('Time (s): '); disp(' ') disp('Velocity (m/s): ') vel = sqrt(g*m/cd)*tanh(sqrt(g*cd/m)*t); disp([t; vel]’)

Interactive M-File >> freefallinteract Mass (kg): 68. 1 Drag coefficient (kg/m): 0. 25 Time (s): 0: 1: 20 Velocity (m/s): 0 0 1. 0000 9. 6939 2. 0000 18. 7292 3. 0000 26. 6148 4. 0000 33. 1118 5. 0000 38. 2154 6. 0000 42. 0762 7. 0000 44. 9145 8. 0000 46. 9575 9. 0000 48. 4058 10. 0000 49. 4214 11. 0000 50. 1282 12. 0000 50. 6175 13. 0000 50. 9550 14. 0000 51. 1871 15. 0000 51. 3466 16. 0000 51. 4560 17. 0000 51. 5310 18. 0000 51. 5823 19. 0000 51. 6175 20. 0000 51. 6416

CVEN 302 -501 Homework No. 2 n n n Chapter 3 Problems 3. 1 (25), 3. 4 (25) Due Wed. 09/10/2008 at the beginning of the period

Common Program Structures n n n Sequence Selection Repetition

Structured Programming Modular Design n Subroutines (function M-files) called by a main program Top-Down Design n a systematic development process that begins with the most general statement of a program’s objective and then successively divides it into more detailed segments Structured Programming n deals with how the actual code is developed so that it is easy to understand, correct, and modify

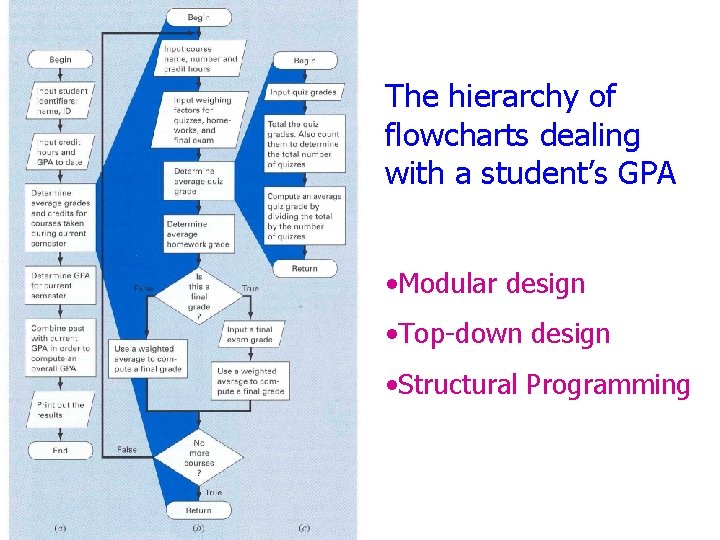
The hierarchy of flowcharts dealing with a student’s GPA • Modular design • Top-down design • Structural Programming

Structured Programming n n n n The ideal style of programming is Structured or Modular programming Break down a large goal into smaller tasks Develop a module for each task A module has a single entrance and exit Modules can be used repeatedly A subroutine (function M-file) may contain several modules Subroutines (Function M-files) called by a main program

Algorithm Design The sequence of logical steps required to perform a specific task (solve a problem) n n Each step must be deterministic The process must always end after a finite number of steps An algorithm cannot be open-ended The algorithm must be general enough to deal with any contingency

Structured Programming Sequential paths n Sequence – all instructions (statements) are executed sequentially from top to bottom * A strict sequence is highly limiting Non-sequential paths n Decisions (Selection) – if, elseif n Loops (Repetition) – for, while, break

Selection (IF) Statements n n The most common form of selection structure is simple if statement The if statement will have a condition associated with it The condition is typically a logical expression that must be evaluated as either “true” or “false” The outcome of the evaluation will determine the next step performed

Logical IF Statements n If (condition) executable_statements end if (x < = -1. 0 | x > = 1. 0) y = 0. end if (x > -1. 0 & x < 0. ) y = 1. + x end if (x > = 0. & x < 1. 0) y = 1. - x end y 1 -1 1 x

Relation Operators n n n n n MATLAB == ~= < <= > >= & | ~ n n n n n Interpretation is equal to is not equal to is less than or equal to is greater than or equal to and, true if both are true or, true if either one is true not

Logical Conditions Ø ~ (not) – logical negation of an expression ~ expression n If the expression is true, the result is false. Conversely, if the expression is false, the result is true. Ø & (and) – logical conjunction on two expressions expression 1 & expression 2 n If both expressions are true, the result is true. If either or both expressions are false, the result is false. Ø | (or) – logical disjunction on two expressions expression 1 | expression 2 n If either or both expressions are true, the result is true

Logical Operators n n 0 - 1 matrix 0: false ; 1: True

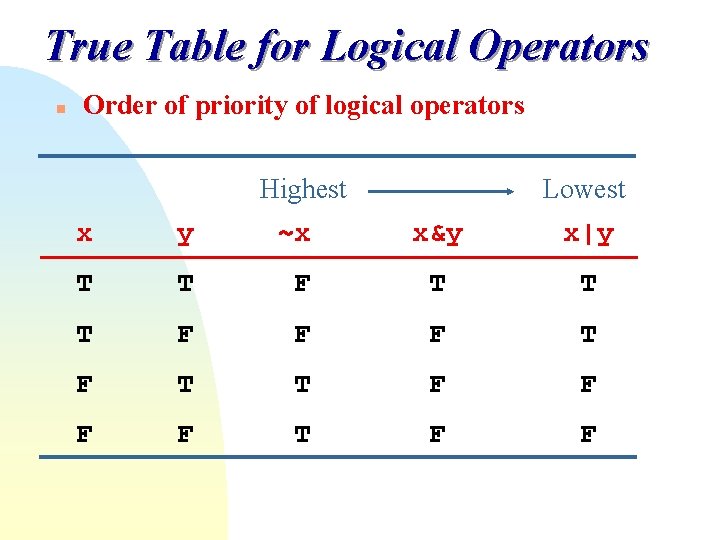
True Table for Logical Operators n Order of priority of logical operators Highest Lowest x y ~x x&y x|y T T F T T T F F F T T F F

Example of a Complex Decision If a=-1, b=2, x=1, and y=‘b’, evaluate A * b > 0 & b == 2 & x > 7 | ~(y > ‘d’) 1. Expression 1: A*b = -2 > 0 (false) 2. Expression 2: b = 2 (true) 3. Expression 3: x = 1 > 7 (false) 4. Expression 4: ‘b’ > ‘d’ (false) 5. Expression 5: ~(Expression 4) (true) 6. Expression 6: (Expression 1) & (Expression 2) (false) 7. Expression 7: (Expression 6) & (Expression 3) (false) 8. Expression 8: (Expression 7) | (Expression 5) (true)

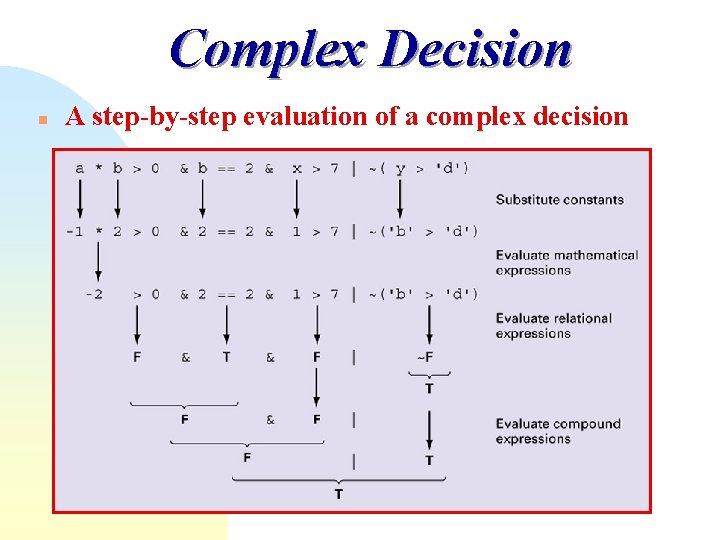
Complex Decision n A step-by-step evaluation of a complex decision

Nested IF Statement Ø Structures can be nested within each other if (condition) statement block elseif (condition) another statement block else another statement block end

How to use Nested IF n n If the condition is true the statements following the statement block are executed. If the condition is not true, then the control is transferred to the next else, elseif, or end statement at the same if level.

Else and Elseif if temperature > 100 disp(‘Too hot - equipment malfunctioning. ’) elseif temperature > 75 disp(‘Normal operating range. ’) elseif temperature > 60 disp(‘Temperature below desired operating range. ’) else disp(‘Too Cold - turn off equipment. ’) end

Nested IF Statements n nested if (if, if elseif) if (x < = -1. 0) y = 0. elseif (x < = 0. ) y = 1. + x elseif (x < = 1. 0) y 1 y = 1. - x else y=0. end -1 1 x

M-file: Evaluate CVEN 302 Grade function cven 302_grade name = input('Enter Student Name: ', 's'); sid = input('Enter Student ID: '); HW = input('Enter Homework Average (30%): '); Exam 1 = input('Enter Exam I score (20%): '); Exam 2 = input('Enter Exam II score (20%): '); Final = input('Enter Final Exam score (30%): '); Average= HW*0. 3 + Exam 1*0. 2 + Exam 2*0. 2 + Final*0. 3; fprintf('Your Semester Average is: %6. 2 f n', Average) if Average >= 90 Grade = 'A'; elseif Average >= 80 Grade = 'B'; elseif Average >= 70 Grade = 'C'; elseif Average >= 60 Grade = 'D'; else Grade = 'F'; end fprintf('Your Semester Grade is : '), disp(Grade)

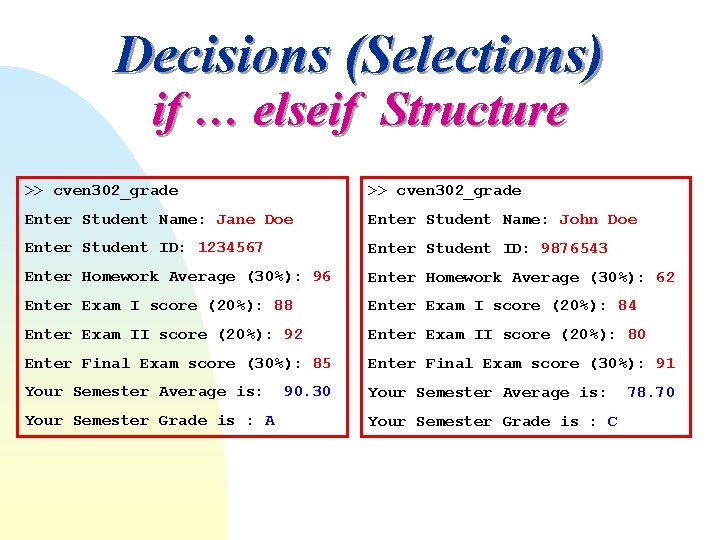
Decisions (Selections) if … elseif Structure >> cven 302_grade Enter Student Name: Jane Doe Enter Student Name: John Doe Enter Student ID: 1234567 Enter Student ID: 9876543 Enter Homework Average (30%): 96 Enter Homework Average (30%): 62 Enter Exam I score (20%): 88 Enter Exam I score (20%): 84 Enter Exam II score (20%): 92 Enter Exam II score (20%): 80 Enter Final Exam score (30%): 85 Enter Final Exam score (30%): 91 Your Semester Average is: Your Semester Grade is : A 90. 30 Your Semester Grade is : C 78. 70

Do loops Repetition for i=1: m for j=1: n a(i, j)=(i+1)^2*sin(0. 2*j*pi); end

For Loops for index = start : step : finish statements end Ends after a specified number of repetitions for k = 1: length(d) if d(k) < 30 velocity(k) = 0. 5 - 0. 3*d(k). ^2; else velocity(k) = 0. 6 + 0. 2*d(k)-0. 01*d(k). ^2 end

For Loop function A = for_loop(m, n) for i = 1: m for j = 1: n A(i, j) = 50*exp(-0. 2*i)^2*sin(0. 1*j*pi); end >> A = for_loop(8, 6) A = 10. 3570 19. 7002 27. 1150 31. 8756 33. 5160 31. 8756 6. 9425 13. 2054 18. 1757 21. 3669 22. 4664 21. 3669 4. 6537 8. 8519 12. 1836 14. 3226 15. 0597 14. 3226 3. 1195 5. 9336 8. 1669 9. 6007 10. 0948 9. 6007 2. 0910 3. 9774 5. 4744 6. 4356 6. 7668 6. 4356 1. 4017 2. 6661 3. 6696 4. 3139 4. 5359 4. 3139 0. 9396 1. 7872 2. 4598 2. 8917 3. 0405 2. 8917 0. 6298 1. 1980 1. 6489 1. 9384 2. 0381 1. 9384

For Loop n n M-file for computing the factorial n! MATLAB has a built-in function factorial(n) to compute n! function fout = factor(n) % factor(n): % Computes the product of all the integers from 1 to n. x=1; for i = 1: n x = x*i; end fout = x; >> factor(12) >> factor(100) ans = 479001600 9. 332621544394410 e+157

While Loops while condition statements end Ends on the basis of a logical condition Ø If the statement is true, the statements are executed Ø If the statement is always true, the loop becomes an “infinite loop” Ø The “break” statement can be used to terminate the “while” or “for” loop prematurely.

While Loop Ø Compute your checking account balance function checking % Compute balance in checking account Balance = input('Current Checking Account Balance ($) = '); Deposit = input('Monthly Deposit ($) = '); Subtract = input('Monthly Subtractions ($) = '); Month = 0; while Balance >= 0 Month = Month + 1; Balance = Balance + Deposit - Subtract; if Balance >= 0 fprintf('Month %3 d Account Balance = %8. 2 f n', Month, Balance) fprintf('Month %3 d Account Closed n', Month) else end

While Loop >> checking Current Checking Account Balance ($) = 8527. 20 Monthly Deposit ($) = 1025. 50 Monthly Subtractions ($) = 1800 Month 1 Account Balance = 7752. 70 Month 2 Account Balance = 6978. 20 Month 3 Account Balance = 6203. 70 Month 4 Account Balance = 5429. 20 Month 5 Account Balance = 4654. 70 Month 6 Account Balance = 3880. 20 Month 7 Account Balance = 3105. 70 Month 8 Account Balance = 2331. 20 Month 9 Account Balance = 1556. 70 Month 10 Account Balance = 782. 20 Month 11 Account Balance = 7. 70 Month 12 Account Closed

Nesting and Indentation n Example: Roots of a Quadratic Equation Ø If a=0, b=0, no solution (or trivial sol. c=0) Ø If a=0, b 0, one real root: x=-c/b Ø If a 0, d=b 2 4 ac 0, two real roots Ø If a 0, d=b 2 4 ac <0, two complex roots

Nesting and Indentation function quad = quadroots(a, b, c) % Computes real and complex roots of quadratic equation % a*x^2 + b*x + c = 0 % Output: (r 1, i 1, r 2, i 2) - real and imaginary parts of the % first and second root if a == 0 % weird cases if b ~= 0 % single root r 1 = -c/b else % trivial solution error('Trivial or No Solution. Try again') end % quadratic formula else d = b^2 - 4*a*c; % discriminant if d >= 0 % real roots r 1 = (-b + sqrt(d)) / (2*a) r 2 = (-b - sqrt(d)) / (2*a) else % complex roots r 1 = -b / (2*a) r 2 = r 1 i 1 = sqrt(abs(d)) / (2*a) i 2 = -i 1 end

Roots of Quadratic Equation >> quad = quadroots(5, 3, -4) r 1 = 0. 6434 r 2 = -1. 2434 >> quad = quadroots(5, 3, 4) r 1 = -0. 3000 r 2 = -0. 3000 i 1 = 0. 8426 i 2 = -0. 8426 (two real roots) (two complex roots) >> quad = quadroots(0, 0, 5) ? ? ? Error using ==> quadroots Trivial or No Solution. Try again (no root)

Passing Functions to M-File n Use built-in “feval” and “inline” functions to perform calculations using an arbitrary function outvar = feval(‘funcname’, arg 1, arg 2, …) Funcname = inline(‘expression’, var 1, var 2, . . . ) >> fx=inline('exp(-x)*cos(x)^2*sin(2. *x)') fx = Inline function: fx(x) = exp(-x)*cos(x)^2*sin(2. *x) >> y = fx(2/3*pi) y = -0. 0267 No need to store in separate M -file

Bungee Jumper: Euler’s Method function [x, y] = Euler(f, tspan, y 0, n) % solve y' = f(x, y) with initial condition y(a) = y 0 % using n steps of Euler's method; step size h = (b-a)/n % tspan = [a, b] a = tspan(1); b = tspan(2); h = (b - a) / n; x = (a+h : b); y(1) = y 0 + h*feval(f, a, y 0); for i = 2 : n y(i) = y(i-1) + h*feval(f, x(i-1), y(i-1)); end x = [ a x ]; y = [y 0 y ]; Use “feval” for function evaluation function f = bungee_f(t, v) % Solve dv/dt = f for bungee jumper velocity g = 9. 81; m = 68. 1; cd = 0. 25; f = g - cd*v^2/m;

MATLAB M-File: Bungee Jumper [t, v] = bungee_exact; hold on; % Exact Solution [t 1, v 1] = Euler('bungee_f', [0 20], 0, 10); % Euler method h 1=plot(t 1, v 1, 'g-s'); set(h 1, 'Line. Width', 3, 'Marker. Size', 10); [t 2, v 2] = Euler('bungee_f', [0 20], 0, 20); %Euler method h 2 = plot(t 2, v 2, 'k: d'); set(h 2, 'Line. Width', 3, 'Marker. Size', 10); [t 3, v 3] = Euler('bungee_f', [0 20], 0, 100); %Euler method h 3 = plot(t 3, v 3, 'mo'); hold off; set(h 3, 'Line. Width', 3, 'Marker. Size', 5); h 4 = title('Bungee Jumper'); set(h 4, 'Font. Size', 20); h 5 = xlabel('Time (s)'); set(h 5, 'Font. Size', 20); h 6 = ylabel('Velocity (m/s)'); set(h 6, 'Font. Size', 20); h 7 = legend('Exact Solution', 'Delta t = 2 s', 'Delta t = 1 s‘, 'Delta t = 0. 2 s', 0); set(h 7, 'Font. Size', 20);

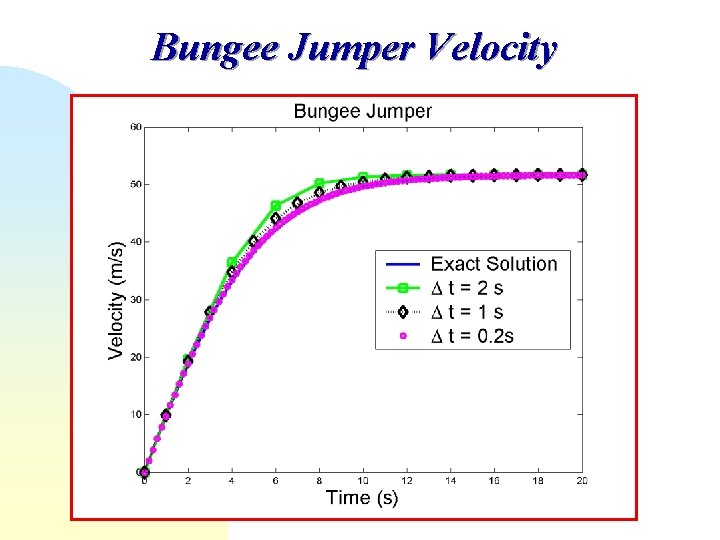
Bungee Jumper Velocity

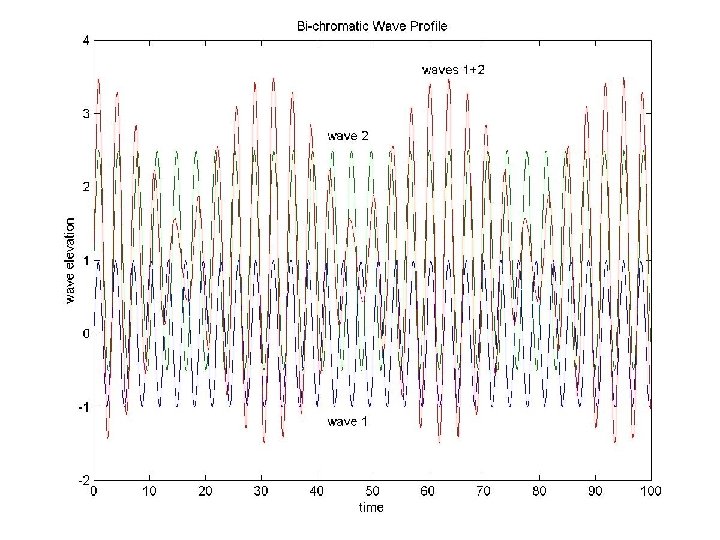
M-File: Bichromatic Waves n Filename waves. m (script file) % Plot Bi-chromatic Wave Profile a 1 = 1; a 2 = 1. 5; c 1 = 2. 0; c 2 = 1. 8; time = 0: 0. 1: 100; wave 1 = a 1 * sin(c 1*time); wave 2 = a 2 * sin(c 2*time) + a 1; wave 3 = wave 1 + wave 2; plot(time, wave 1, time, wave 2, time, wave 3) axis([0 100 -2 4]); xlabel ('time'); ylabel ('wave elevation'); title ('Bi-chromatic Wave Profile') text(42, -1. 2, 'wave 1') text(42, 2. 7, 'wave 2') text(59, 3. 6, 'waves 1+2')

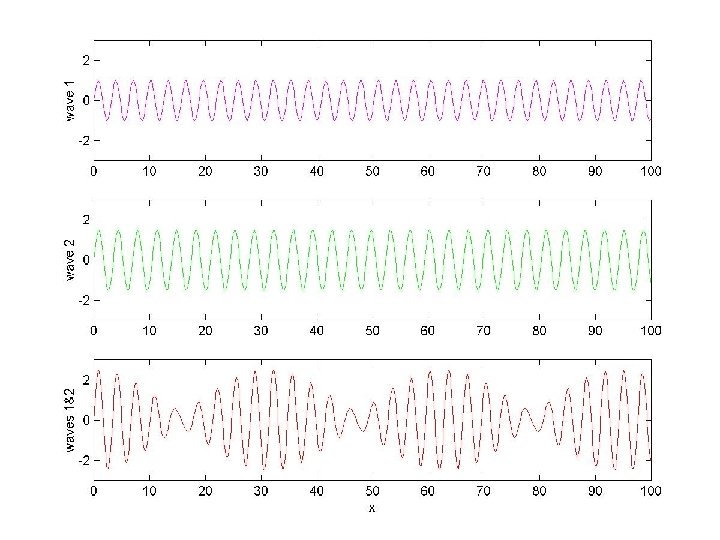
MATLAB Subplots n Filename waves 2. m (script file) % Plot Bi-chromatic Wave Profile % Display the results in three subplots clf % clear the graphics window a 1 = 1; a 2 = 1. 5; c 1 = 2. 0; c 2 = 1. 8; time = 0: 0. 1: 100; wave 1 = a 1 * sin(c 1*time); wave 2 = a 2 * sin(c 2*time); wave 3 = wave 1 + wave 2; subplot(3, 1, 1) % top figure plot(time, wave 1, 'm'); axis([0 100 -3 3]); ylabel('wave 1'); subplot(3, 1, 2) % middle figure plot(time, wave 2, 'g'); axis([0 100 -3 3]); ylabel('wave 2'); subplot(3, 1, 3) % bottom figure plot(time, wave 3, 'r'); axis([0 100 -3 3]); xlabel(’time'); ylabel('waves 1&2');

MATLAB Subplots subplot ( m, n, p ) -breaks the figure window into m by n small figures, select the p-th figure for the current plot » figure (3) » subplot (3, 2, 1) » plot (t, wv 1) » subplot (3, 2, 2) » plot (t, wv 2) » subplot (3, 2, 4) » plot (t, wv 1+wv 2) » subplot (3, 2, 6) » plot (t, wv 1 -wv 2) 1 2 3 4 5 6

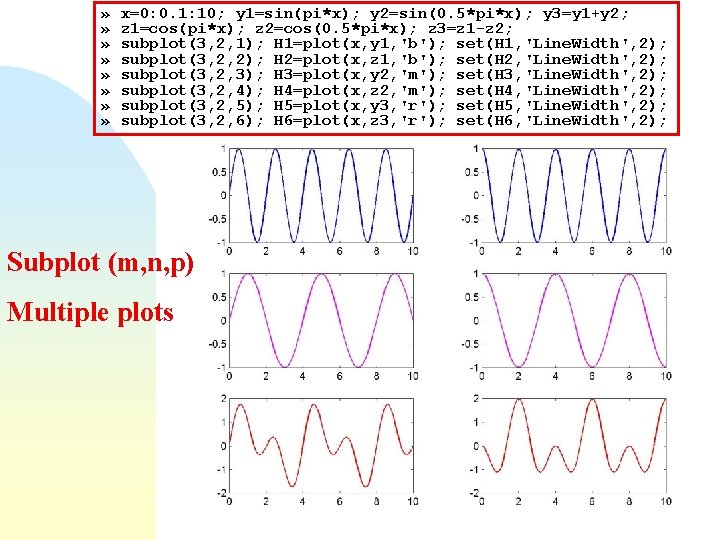
» » » » x=0: 0. 1: 10; y 1=sin(pi*x); y 2=sin(0. 5*pi*x); y 3=y 1+y 2; z 1=cos(pi*x); z 2=cos(0. 5*pi*x); z 3=z 1 -z 2; subplot(3, 2, 1); H 1=plot(x, y 1, 'b'); set(H 1, 'Line. Width', 2); subplot(3, 2, 2); H 2=plot(x, z 1, 'b'); set(H 2, 'Line. Width', 2); subplot(3, 2, 3); H 3=plot(x, y 2, 'm'); set(H 3, 'Line. Width', 2); subplot(3, 2, 4); H 4=plot(x, z 2, 'm'); set(H 4, 'Line. Width', 2); subplot(3, 2, 5); H 5=plot(x, y 3, 'r'); set(H 5, 'Line. Width', 2); subplot(3, 2, 6); H 6=plot(x, z 3, 'r'); set(H 6, 'Line. Width', 2); Subplot (m, n, p) Multiple plots

CVEN 302 -501 Homework No. 3 n n n Chapter 3 Problems 3. 6 (35), 3. 9 (35) Due Mon 09/15/08 at the beginning of the period