Chapter 3 Probability Sampling Theory Hypothesis Testing 2017

Chapter 3 • Probability • Sampling Theory • Hypothesis Testing © 2017 Taylor & Francis

Probability • The extent to which something is likely to happen • “On average” • Distribution of outcomes © 2017 Taylor & Francis

“On Average” • Probability is based upon an infinite number of chances • The concept “on average” implies the likelihood, the probability, of a particular outcome given an infinite number of possible outcomes © 2017 Taylor & Francis

Distribution of Outcomes • Permutations: the number of ways a result can occur where order is important • Combinations: the number of ways a result can occur without regard to order © 2017 Taylor & Francis

Example • Coincidence game © 2017 Taylor & Francis

Hypothesis Testing © 2017 Taylor & Francis

What is a Hypothesis • Definition: A statement of relationship between variables. © 2017 Taylor & Francis

Null Hypothesis • Null hypothesis: a statement of no relationship between variables (a negation of the research hypothesis) • A test of • A null hypothesis can be rejected or not rejected © 2017 Taylor & Francis

Significance • Before we test a hypothesis, we must decide how much error is acceptable • Social scientists generally accept 5%, on average • Something is considered significant when the chances that the relationship exists are 95% or greater (less than 5% chance of error) © 2017 Taylor & Francis

Statements of Error • Type I Error: the error of rejecting a null hypothesis, rejecting coincidence, and claiming support for the research hypothesis • Type II Error: concluding that the result is due to random coincidence when it is actually not; fail to correctly reject the null hypothesis and support the research hypothesis © 2017 Taylor & Francis
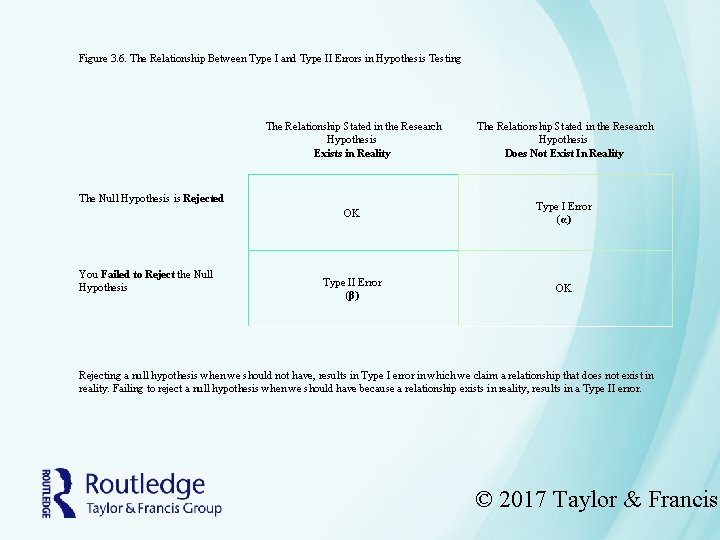
Figure 3. 6. The Relationship Between Type I and Type II Errors in Hypothesis Testing The Null Hypothesis is Rejected You Failed to Reject the Null Hypothesis The Relationship Stated in the Research Hypothesis Exists in Reality The Relationship Stated in the Research Hypothesis Does Not Exist In Reality OK Type I Error (α) Type II Error (β) OK Rejecting a null hypothesis when we should not have, results in Type I error in which we claim a relationship that does not exist in reality. Failing to reject a null hypothesis when we should have because a relationship exists in reality, results in a Type II error. © 2017 Taylor & Francis

Significance and Error • Type I error, alpha (α): the acceptable level of error for rejecting the null hypothesis • Detecting an effect that is not present • False positive © 2017 Taylor & Francis

Significance and Error • Type II error, beta (β): important for small sample sizes; failure to reject the null hypothesis when a relationship occurs • Not detecting an effect that is present • False negative • Power = 1 - β © 2017 Taylor & Francis
- Slides: 13