Chapter 3 Preferences Intermediate Microeconomics A ToolBuilding Approach

Preferences as rankings • How would you rank an apple and a banana? (1) An apple is better than a banana (2) A banana is better than an apple (3) An apple is as good as a banana

Rankings as binary relations • Set of objects: X • Binary relation: R defined over any two elements of X “is related to” • Ex. 1: X = students in class R = is taller than R relates any pair from X unless they are the same height • Ex. 2: X = students in class R = is a sibling of R does not relate any pair from X unless they are siblings

Preferences as binary relations For a decision-maker, we have the set of objects to choose from, E. g. , fruits, students, candidates in an election X = {A, B, C, D, …} and preferences (binary relations) over these objects = is at least as good as Then, A B means [A “is preferred to” A B means [A “is indifferent to” B & not B B & B A] Primitive (given) A] Strict preference (derived from primitive) Indifference (derived from primitive)

Properties of binary relations • Ex. 3: X = students in class R = is the same age (born on the same day) or older than (born on an earlier day) P 1 • Pick any single item, x, from X. Is x R x? Yes: R is reflexive P 2 • Pick any two different items, x and y, from X. Is either x R y, or y R x, or both? Yes: R is total P 3 • Pick any three items, x, y, and z, satisfying x R y and y R z. Is x R z? Yes: R is transitive

Properties of preferences Ex. 4: For consumers, the ranking is of commodity bundles X = the commodity space, = is at least as good as We say preferences are regular if is reflexive, total and transitive, i. e. , satisfies P 1, P 2, and P 3. Two more properties P 4 • Monotonicity P 5 • Convexity (to be covered later)

Strict monotonicity • Captures the idea that “goods are good” • More of at least one good is better Strictly better than A = (4, 3) B A C A D A Strictly worse than A = (4, 3)

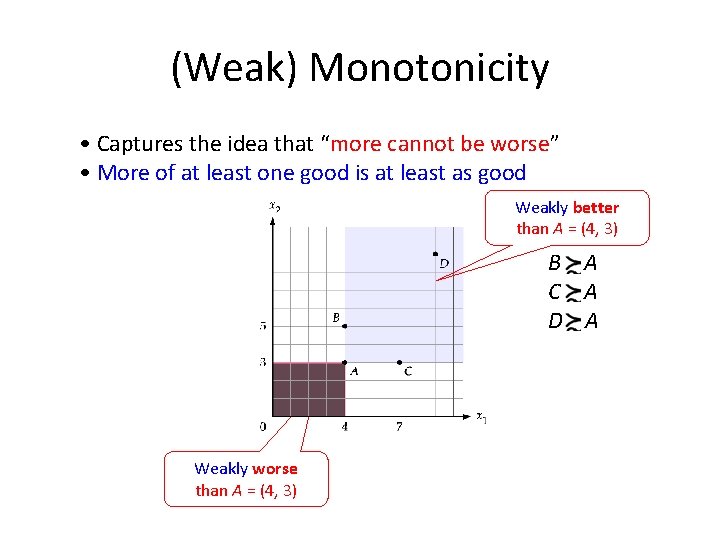
(Weak) Monotonicity • Captures the idea that “more cannot be worse” • More of at least one good is at least as good Weakly better than A = (4, 3) B A C A D A Weakly worse than A = (4, 3)

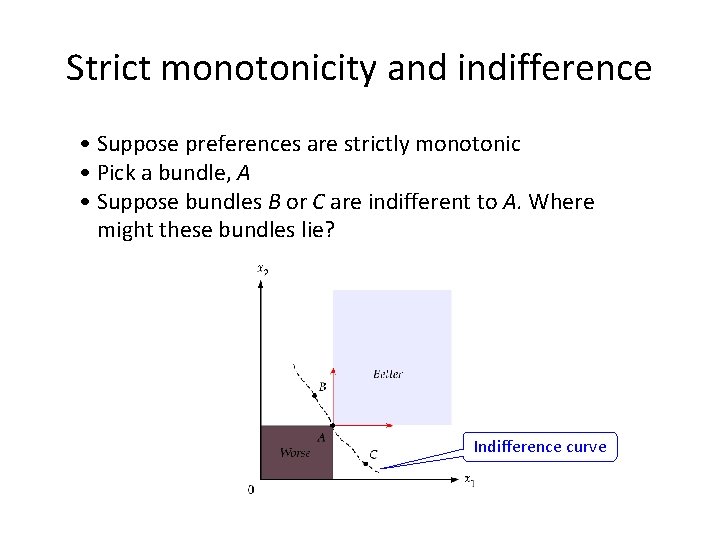
Strict monotonicity and indifference • Suppose preferences are strictly monotonic • Pick a bundle, A • Suppose bundles B or C are indifferent to A. Where might these bundles lie? Indifference curve

Utility Representation • Suppose there is a utility function u that associates a real number with every object in X • Then u(P) is the utility level of object P Given preferences on X, a utility function u represents the preferences means if P Q, then u(P) ≥ u(Q), and vice versa • The “vice versa” part means that given a utility function, it is possible to figure out the underlying preferences • A utility function preserves the same ranking over the objects as the underlying preferences

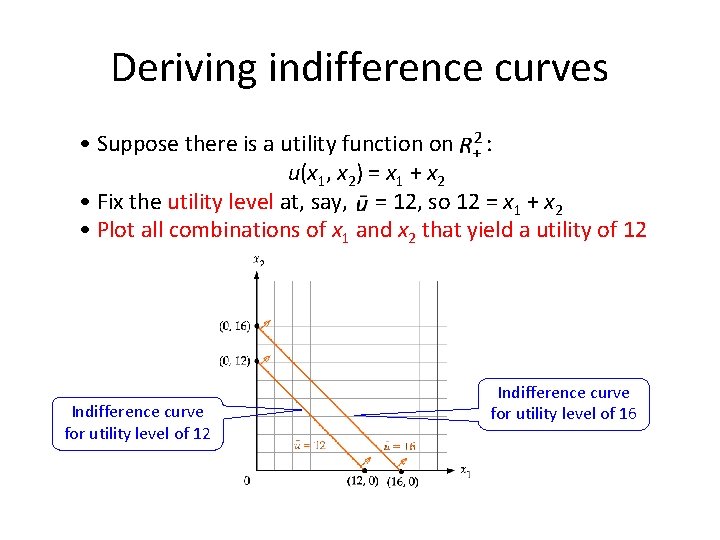
Deriving indifference curves • Suppose there is a utility function on : u(x 1, x 2) = x 1 + x 2 • Fix the utility level at, say, = 12, so 12 = x 1 + x 2 • Plot all combinations of x 1 and x 2 that yield a utility of 12 Indifference curve for utility level of 16

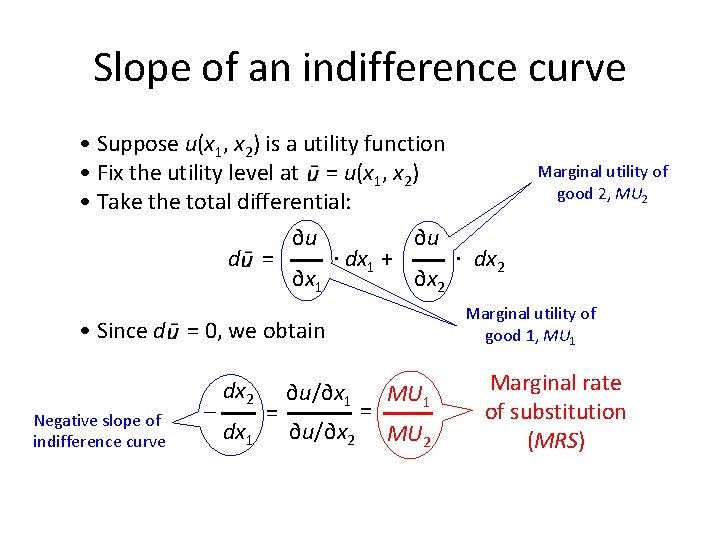
Slope of an indifference curve • Suppose u(x 1, x 2) is a utility function • Fix the utility level at = u(x 1, x 2) • Take the total differential: ∂u ∂u. dx 1 +. dx 2 d = ∂x 1 ∂x 2 Marginal utility of good 1, MU 1 • Since d = 0, we obtain Negative slope of indifference curve – dx 2 dx 1 = ∂u/∂x 1 ∂u/∂x 2 Marginal utility of good 2, MU 2 = MU 1 MU 2 Marginal rate of substitution (MRS)

Types of preferences • There are many preferences satisfying P 1–P 5 • Four basic ones – Linear: u(x 1, x 2) = ax 1 + bx 2 – Leontief: u(x 1, x 2) = min {ax 1, bx 2} – Quasilinear: u(x 1, x 2) = f(x 1) + x 2, or u(x 1, x 2) = x 1 + f(x 2) – Cobb-Douglas: u(x 1, x 2) = A(x 1)a(x 2)b *The function f is generally increasing and strictly concave, i. e. , f ’ > 0 and f ” < 0

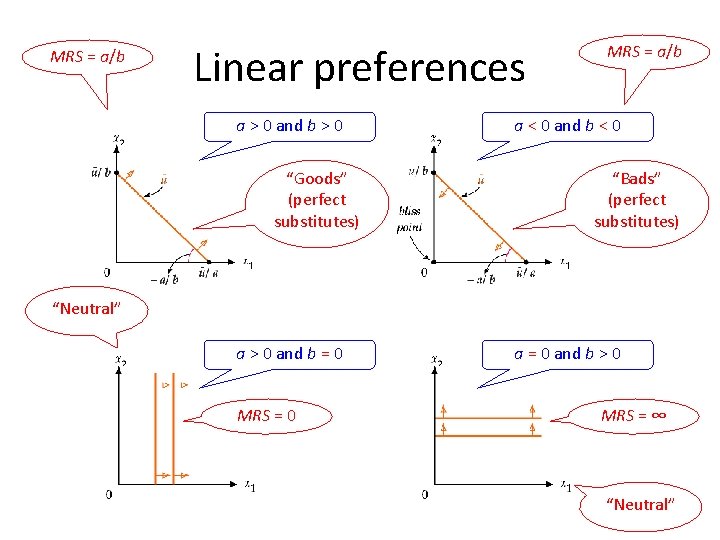
MRS = a/b Linear preferences a > 0 and b > 0 “Goods” (perfect substitutes) MRS = a/b a < 0 and b < 0 “Bads” (perfect substitutes) “Neutral” a > 0 and b = 0 MRS = 0 and b > 0 MRS = ∞ “Neutral”

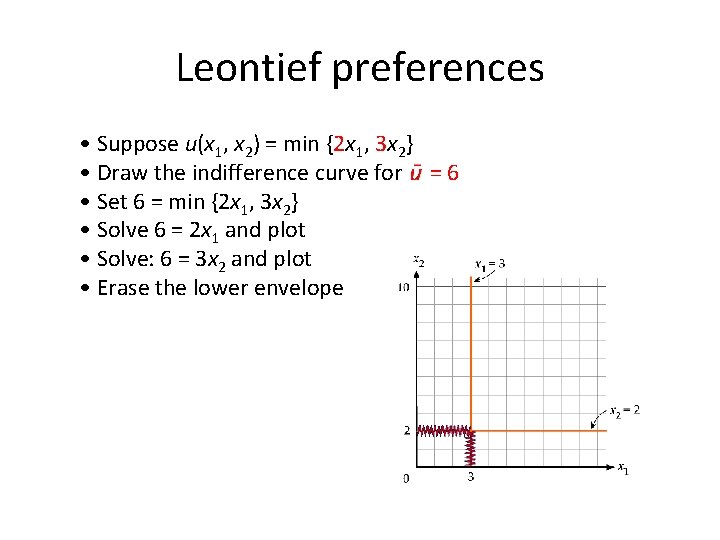
Leontief preferences • Suppose u(x 1, x 2) = min {2 x 1, 3 x 2} • Draw the indifference curve for = 6 • Set 6 = min {2 x 1, 3 x 2} • Solve 6 = 2 x 1 and plot • Solve: 6 = 3 x 2 and plot • Erase the lower envelope

Leontief preferences • Suppose u(x 1, x 2) = min {ax 1, bx 2} • Draw the ray through the origin with slope a/b • All indifference curves will have kinks along this ray • The goods are perfect complements x 1 and x 2 are consumed in fixed proportions • There is no MRS!

Quasilinear preferences • Suppose u(x 1, x 2) = √x 1 + x 2 • Draw the indifference curves for utility levels 4, 8, 12, 20 • Indifference curves are ‘vertically parallel’ • The MRS is the same along any vertical line

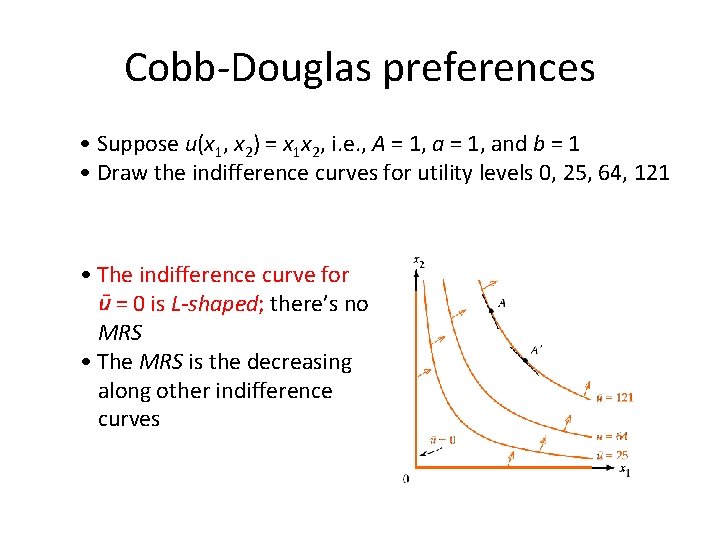
Cobb-Douglas preferences • Suppose u(x 1, x 2) = x 1 x 2, i. e. , A = 1, and b = 1 • Draw the indifference curves for utility levels 0, 25, 64, 121 • The indifference curve for = 0 is L-shaped; there’s no MRS • The MRS is the decreasing along other indifference curves

Utility is ordinal • Suppose u = x 1 + x 2 for consumer Teri • Suppose v = 2 x 1 + 2 x 2 for consumer Toni, Teri’s twin • How do their preferences, i. e. , ranking of bundles, differ? • They don’t! • They both like A over B • They are both indifferent between A and C • Teri and Toni’s MRS = 1 • Their indifference curves just have different values • They have the same preferences

Positive monotonic transformations • If v = f(u) where f ’ > 0 and f ” < 0 for positive u, then v is a positive monotonic transformation (PMT) of u • Ex. 1: v = ur, where r > 0 • Ex. 2: v = ln u • Ex. 3: v = a + bu, where a > 0 and b > 0 • Ex. 4: v = eu • If v is a PMT of u, then they represent the same preferences — the set of indifference curves under u are the same as the set of indifference curves under v — at any bundle, the MRS is the same

Convex sets • Pick any two points in the set S • Join them with a straight line • If the line lies within S, then S is a convex set A strictly convex set Not a convex set A weakly convex set

Convex preferences P 5 • Pick any commodity bundle A in • Ex. 1: Leontief preferences • Draw the indifference curve that passes through A • Find all bundles that are at least as good as A, the weakly-better-than A set, Preferences are convex if the set is a convex set

Strictly convex preferences • Pick any commodity bundle A in • Ex. 2: Cobb-Douglas preferences • Draw the indifference curve that passes through A • Find all bundles that are at least as good as A, the weakly-better-than A set, Preferences are strictly convex if the set is a strictly convex set

Meaning of convex preferences 1. Consumers prefer averages to extremes • Pick A on an indifference curve with little x 1 and lots of x 2 • Pick B on an indifference curve with little x 2 and lots of x 1 • Join them • Any point on this line like C is preferred to A or B

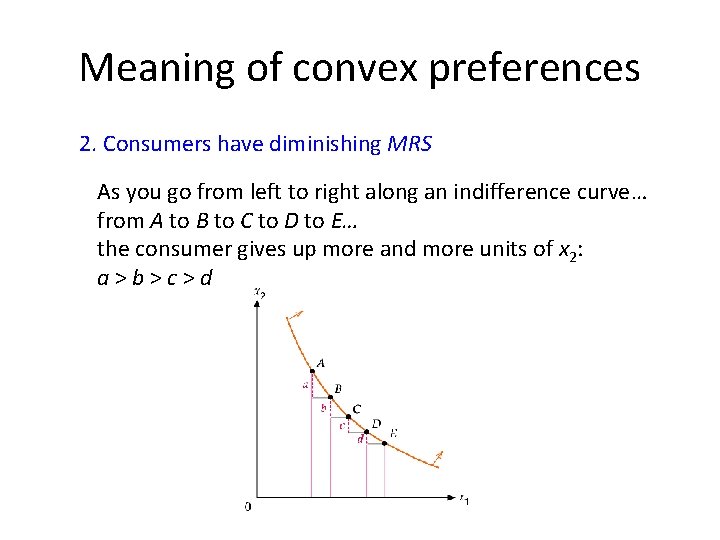
Meaning of convex preferences 2. Consumers have diminishing MRS As you go from left to right along an indifference curve… from A to B to C to D to E… the consumer gives up more and more units of x 2: a>b>c>d