Chapter 3 Planning and Scheduling Lesson Plan n

Chapter 3: Planning and Scheduling Lesson Plan n Scheduling Tasks q q Assumptions and Goals List-Processing Algorithm Optimal Schedules Strange Happenings n Critical-Path Schedules n Independent Tasks q Decreasing-Time-List Algorithm n Bin Packing q Bin-Packing Heuristics q Decreasing-Time Heuristics n Resolving Conflict via Coloring q Vertex Coloring and Chromatic Number 1

Chapter 3: Planning and Scheduling Critical Path Analysis n Critical Path Analysis q Most often, scheduling jobs consists of complicated tasks that cannot be done in a random order. q Due to a pre-defined order of tasks, the entire job may not be done any sooner than the longest path of dependent tasks. n Order-Requirement Digraph q A directed graph (digraph) that shows which tasks precede other tasks among the collection of tasks making up a job. n Critical Path q The longest path in an order-requirement digraph. q The length is measured in terms of summing the task times of the tasks making up the path. An order-requirement digraph, tasks A – E with task times in the circles Critical Path is BE = 25 + 27 = 52 min. 2

Chapter 3: Planning and Scheduling Tasks n Planning and Scheduling q Accurate planning and scheduling is required of both people and machines. n Examples: Around-the-clock scheduling of doctors and nurses, scheduling equipment (X-rays, MRI scans) for maximum efficiency n Processors q A person, machine, robot, operating room, or runway (for airplanes) whose time must be scheduled. n Machine-Scheduling Problem q The problem of deciding how the tasks should be scheduled so the entire job is completed as early as possible. 3

Chapter 3: Planning and Scheduling Tasks n Assumptions q When a processor starts a task, it will be completed without interruption. q Any processor can work on any of the tasks. q No processor stays idle voluntarily. q Order-requirement digraph is used to show the task order and has the task times highlighted within each vertex. q Priority lists arrange the tasks in order, independent of the order requirements. Used to “break ties” if more than one task is ready. n Goals to Consider q Minimize the completion time of the job. q Minimize the total time the processors are idle. q Find the minimum number of processors necessary to finish the job by a specified time. 4

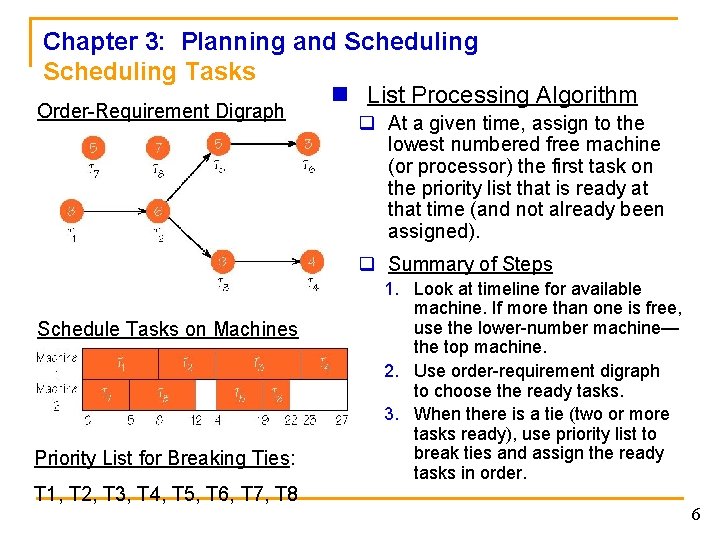
Chapter 3: Planning and Scheduling Tasks n Order-Requirement Digraph q For the next example, tasks are labeled as T 1–T 8. q The length of time for each task is indicated in a colored circle. q At the beginning (time = 0), tasks T 1, T 7, T 8 are ready to be scheduled on machines. n Processors Order Requirement Digraph — Example Ready task – A task is ready if its predecessors have been completed by that time as given by the orderrequirement digraph. q For this example, tasks will be scheduled on two machines according to the order-requirement digraph and priority list. n Priority List q A list that ranks the tasks in some criterion of importance. q For the problem, the priority list is T 1, T 2, T 3, T 4, T 5, T 6, T 7, T 8. 5

Chapter 3: Planning and Scheduling Tasks n List Processing Algorithm Order-Requirement Digraph q At a given time, assign to the lowest numbered free machine (or processor) the first task on the priority list that is ready at that time (and not already been assigned). q Summary of Steps Schedule Tasks on Machines Priority List for Breaking Ties: T 1, T 2, T 3, T 4, T 5, T 6, T 7, T 8 1. Look at timeline for available machine. If more than one is free, use the lower-number machine— the top machine. 2. Use order-requirement digraph to choose the ready tasks. 3. When there is a tie (two or more tasks ready), use priority list to break ties and assign the ready tasks in order. 6

Chapter 3: Planning and Scheduling Tasks n When is the schedule optimal? q From Chapter 2, remember the longest path in an order requirement is the critical path. q The earliest time for the job made up of all the tasks is the length of the longest path (critical path) in the order-requirement digraph. q Referring to the previous example: n The critical path is T 1, T 2, T 3, T 4 = 8 + 6 + 9 + 4 = 27. n If the job is completed in the same time as the length of the critical path, this is the earliest completion time possible and it is an optimal schedule. If the schedule completion time = the length of critical path, then the schedule is optimal (earliest completion time). 7

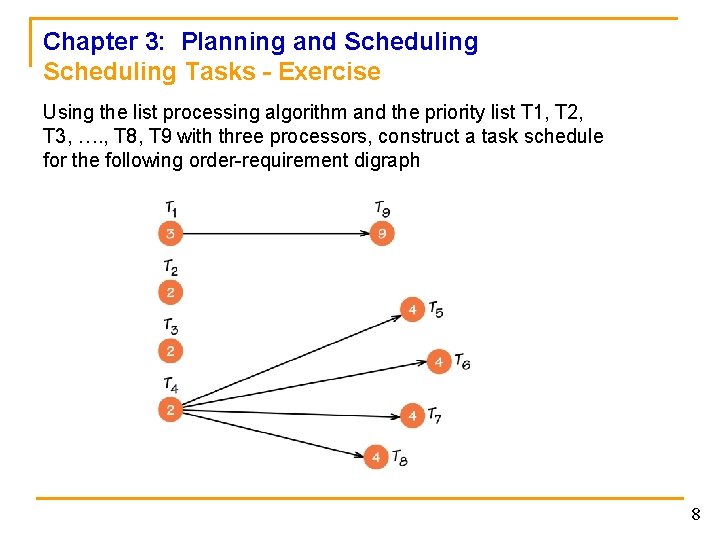
Chapter 3: Planning and Scheduling Tasks - Exercise Using the list processing algorithm and the priority list T 1, T 2, T 3, …. , T 8, T 9 with three processors, construct a task schedule for the following order-requirement digraph 8

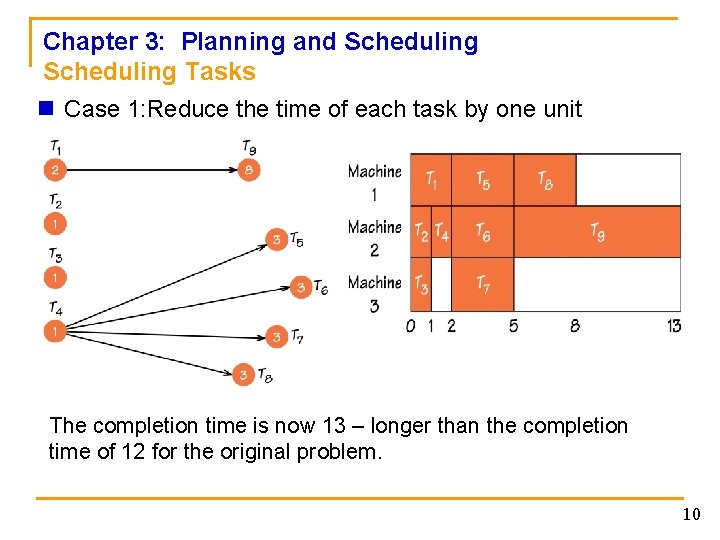
Chapter 3: Planning and Scheduling Tasks n Strange Happenings q Four factors affect the final schedule: 1. Times of the tasks 2. Number of processors 3. Order-requirement diagram 4. Ordering of the tasks on the priority list q While keeping the priority list constant, you would expect the following strategies would make the completion time earlier: 1. Reduce task times. 2. Use more processors. 3. “Loosen” the constraints of the order-requirement digraph. However, with a constant priority list, applying one of these strategies may not always make the completion time shorter — strange happenings. 9

Chapter 3: Planning and Scheduling Tasks n Case 1: Reduce the time of each task by one unit The completion time is now 13 – longer than the completion time of 12 for the original problem. 10

Chapter 3: Planning and Scheduling Tasks n Case 2: Increase the number of processors The completion time is now 15 – longer than the completion time of 12 for the original problem. 11

Chapter 3: Planning and Scheduling Tasks n Case 3: Erase all constraints (edges with arrows) The completion time is now 16 – longer than the completion time of 12 for the original problem. 12

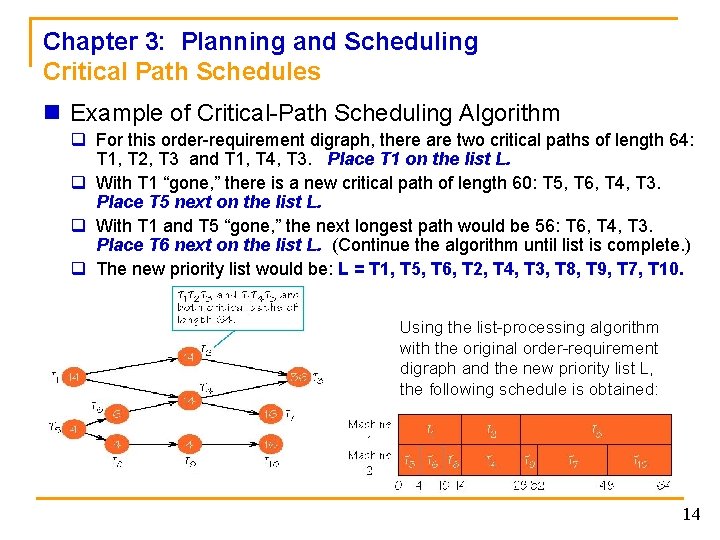
Chapter 3: Planning and Scheduling Critical Path Schedules n Critical-Path Schedules q A systematic method of choosing/creating a priority list, L, that yields optimal, or nearly optimal schedules. n Critical-Path Scheduling Algorithm (to create priority list L) 1. Find a task that heads a critical (longest) path in the orderrequirement digraph. If a tie, choose the lowest-number task. 2. Place the task found in step 1 next on the list L (the first time through the process this task will head the list). 3. Remove the task found in step 1 and the edges attached to it from the current order-requirement digraph, obtaining a new (modified) order-requirement digraph. 4. If there are no vertices left in the new order-requirement digraph, the procedure is complete; if there are vertices left, go to step 1. This procedure will terminate when all the tasks in the original orderrequirement digraph have been placed on the list L (example on next slide). 13

Chapter 3: Planning and Scheduling Critical Path Schedules n Example of Critical-Path Scheduling Algorithm q For this order-requirement digraph, there are two critical paths of length 64: T 1, T 2, T 3 and T 1, T 4, T 3. Place T 1 on the list L. q With T 1 “gone, ” there is a new critical path of length 60: T 5, T 6, T 4, T 3. Place T 5 next on the list L. q With T 1 and T 5 “gone, ” the next longest path would be 56: T 6, T 4, T 3. Place T 6 next on the list L. (Continue the algorithm until list is complete. ) q The new priority list would be: L = T 1, T 5, T 6, T 2, T 4, T 3, T 8, T 9, T 7, T 10. Using the list-processing algorithm with the original order-requirement digraph and the new priority list L, the following schedule is obtained: 14

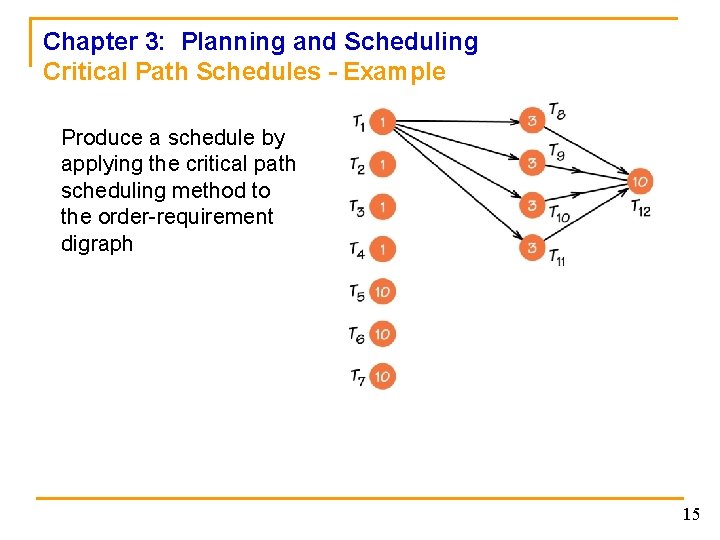
Chapter 3: Planning and Scheduling Critical Path Schedules - Example Produce a schedule by applying the critical path scheduling method to the order-requirement digraph 15

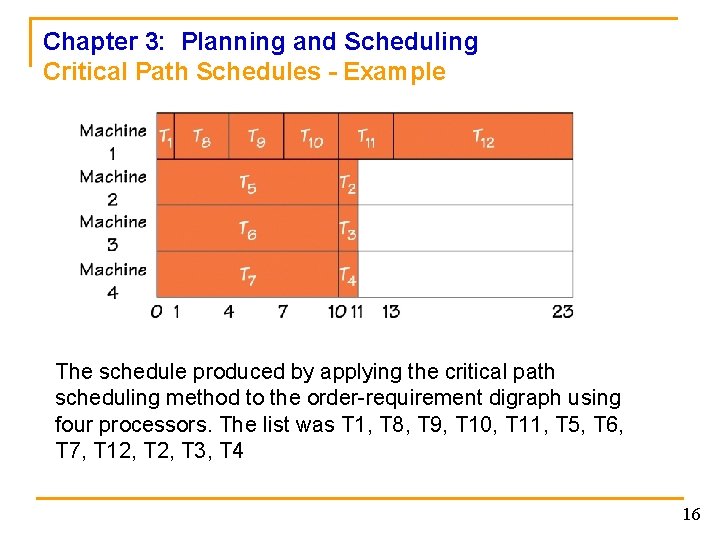
Chapter 3: Planning and Scheduling Critical Path Schedules - Example The schedule produced by applying the critical path scheduling method to the order-requirement digraph using four processors. The list was T 1, T 8, T 9, T 10, T 11, T 5, T 6, T 7, T 12, T 3, T 4 16

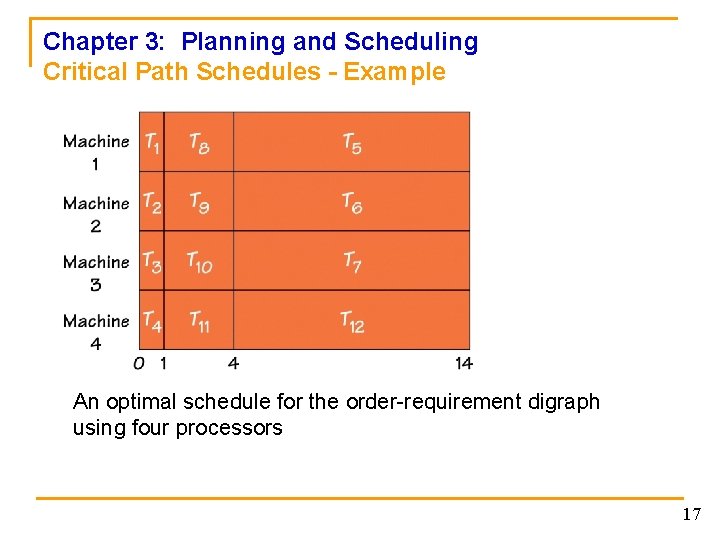
Chapter 3: Planning and Scheduling Critical Path Schedules - Example An optimal schedule for the order-requirement digraph using four processors 17

Chapter 3: Planning and Scheduling Independent Tasks n Independent Tasks q Tasks that are independent of each other if they can be performed in any order (no edges in the order-requirement digraph). q Label the tasks by their task times rather than their task number. q The list-processing algorithm can be used to schedule the tasks onto machines using the given list but may not be efficient. n Decreasing-Time List Algorithm q First put the tasks in decreasing order by time, then apply the list processing algorithm. This will help pack the longest tasks first, so they do not “stick out” on the right end. Example: Apply decreasing-time list algorithm on independent tasks 10, 9, 7, 7, 5, 4 (already in order) This result is an optimal schedule! 18

Chapter 3: Planning and Scheduling Bin Packing n Bin Packing q The problem of finding the minimum number of bins into which the weight can be packed. n Find the minimum number of bins (containers) of capacity, W. n Where weights w 1, w 2, …, wn are packed into the bins. n Each weight of object is less than or equal to W (wi W). q Instead of fixing the number of machines and finding a minimum completion time, we want to find the minimum number of machines (bins), each with a fixed capacity W. n Heuristic Algorithms q Methods that can be carried out quickly but cannot guarantee to produce optimal results. q Once again, there is no fast or optimal algorithm, so we will look at several methods and compare them. 19

Chapter 3: Planning and Scheduling Bin Packing Example: Suppose you plan to build a wall system for your books, CDs, and stereo set. It requires 24 wooden shelves of various length 6, 6, 5, 5, 5, 4, 4, 2, 2, 3, 3, 7, 7, 5, 5, 8, 8, 4, 4, and 5 feet. The lumberyard sells wood only in boards of length 9 feet. If each board costs $80, what is the minimum cost to buy sufficient wood for this wall system? 20

Chapter 3: Planning and Scheduling Bin Packing n Bin Packing — Six Methods Next Fit (NF) First Fit (FF) Worse Fit (WF) Next Fit Decreasing (NFD) First Fit Decreasing (FFD) Worse Fit Decreasing (WFD) q Next Fit (NF) – A new bin is opened if the weight to be packed next will not fit in the bin that is currently being filled; the current bin is then closed. q First Fit (FF) – The next weight to be packed is placed in the lowestnumbered bin already opened into which it will fit. If it does not fit in any open bins, a new bin is opened. q Worse Fit (WF) – The next weight to be packed is placed into the open bin with the largest amount of room remaining. If it does not fit in any bins, open a new bin. q Decreasing-Time Heuristics (NFD, FFD, WFD) – Create the priority list by listing the tasks in order of decreasing size before the binpacking method. 21

Chapter 3: Planning and Scheduling Bin Packing n Next Fit (NF) q Advantages – Does not require knowledge of all the weights in advance; only need to know the remaining space in the current opened bin. q Disadvantages – The bin packed early on may have had room for small items that come later in the list. q Best method for assembly-line packing. n Example Using Next Fit (NF) Bin Packing Total cost = $80*17 = $1, 360 22

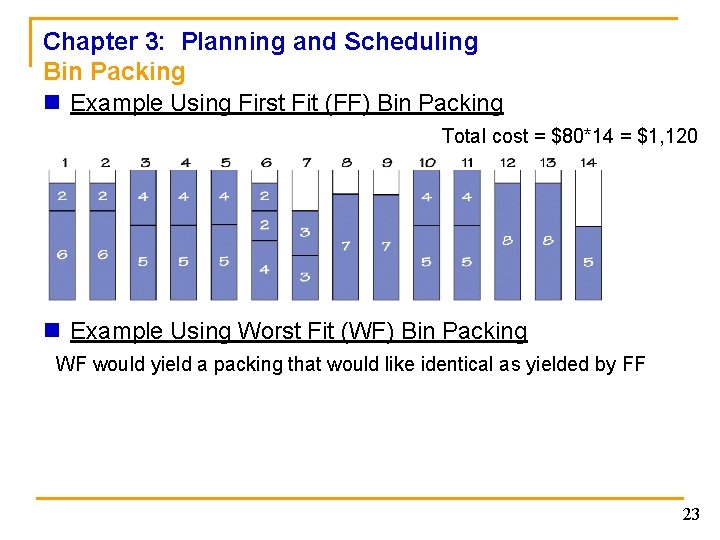
Chapter 3: Planning and Scheduling Bin Packing n Example Using First Fit (FF) Bin Packing Total cost = $80*14 = $1, 120 n Example Using Worst Fit (WF) Bin Packing WF would yield a packing that would like identical as yielded by FF 23

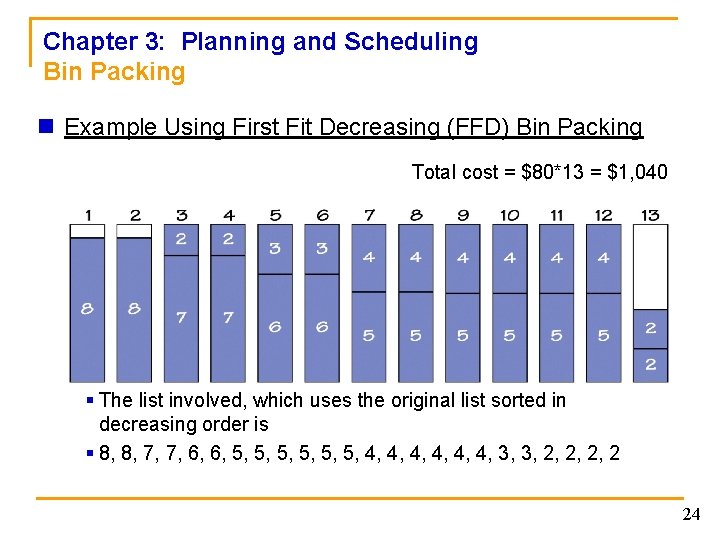
Chapter 3: Planning and Scheduling Bin Packing n Example Using First Fit Decreasing (FFD) Bin Packing Total cost = $80*13 = $1, 040 § The list involved, which uses the original list sorted in decreasing order is § 8, 8, 7, 7, 6, 6, 5, 5, 5, 4, 4, 4, 3, 3, 2, 2 24

Chapter 3: Planning and Scheduling Resolving Conflict n Goals of Three Scheduling Problems q Optimization issues – Try to maximize profit, minimize cost. n Example: Scheduling machine time for earliest completion time q Equity – Try to make things fair for all participants. n Example: Schedule baseball games (same number home and away games) q Conflict Resolution – Try to prevent conflicts from happening. n Example: Scheduling college final examinations for end of term n Resolving Conflict via Coloring q Vertex Coloring – The vertex coloring problem for a graph requires assigning each vertex of the graph a color (label), such that two vertices joined by an edge are assigned different colors. q Chromatic Number – The chromatic number is the minimum number of colors needed to label the vertices of a graph so that no two vertices of the graph joined by an edge get the same color. 25

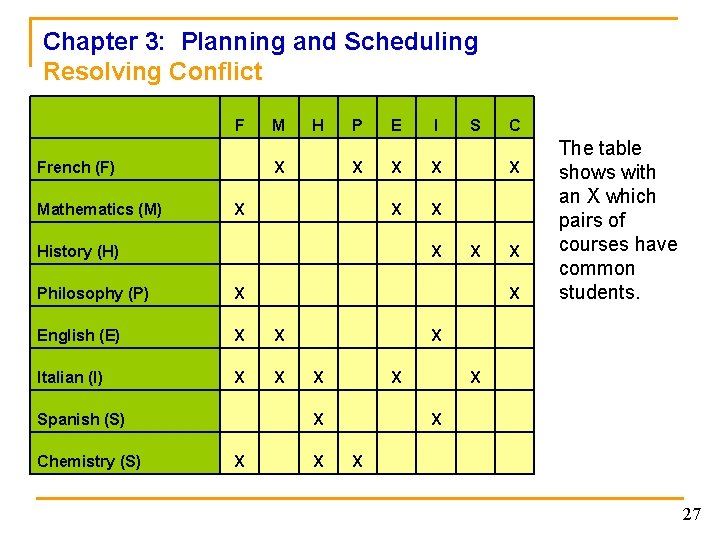
Chapter 3: Planning and Scheduling Resolving Conflict n Example: Scheduling Exams Using Vertex Coloring q There are eight (8) finals to schedule with only two (2) airconditioned rooms. (8 courses: French-F, Math-M, History-H, Philosophy-P, English-E, Italian-I, Spanish-S, Chemistry-C). q In the graph, courses are represented by vertices and two course are joined by an edge for every student enrolled in both courses. 26

Chapter 3: Planning and Scheduling Resolving Conflict F French (F) Mathematics (M) M H X P X X E X X History (H) X Philosophy (P) X English (E) X X Italian (I) X X Spanish (S) Chemistry (S) I C X X The table shows with an X which pairs of courses have common students. X X X S X X 27

Chapter 3: Planning and Scheduling Resolving Conflict n The Problem: Can we assign labels to the vertices of the graph in such a way that vertices that are jointed by an edge get different labels? n If G is a graph (other than a graph where each vertex is joined to every other or a circuit with odd length) with the property that its maximal valance is Δ, then the chromatic number of the graph is at most Δ. 28

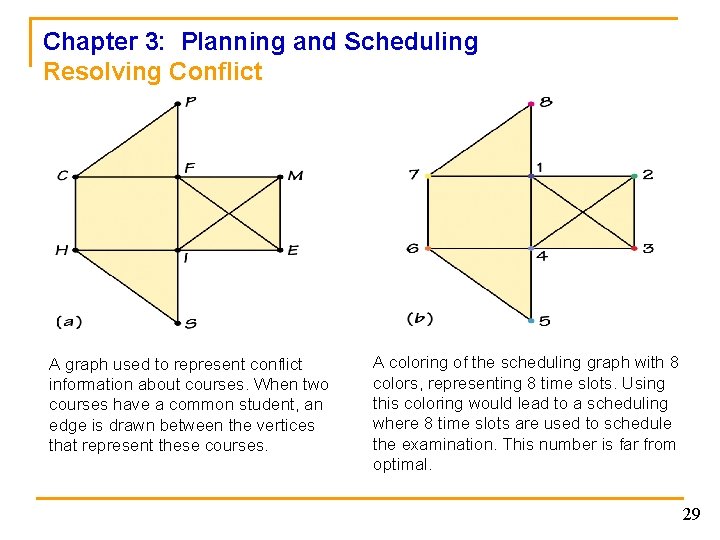
Chapter 3: Planning and Scheduling Resolving Conflict A graph used to represent conflict information about courses. When two courses have a common student, an edge is drawn between the vertices that represent these courses. A coloring of the scheduling graph with 8 colors, representing 8 time slots. Using this coloring would lead to a scheduling where 8 time slots are used to schedule the examination. This number is far from optimal. 29

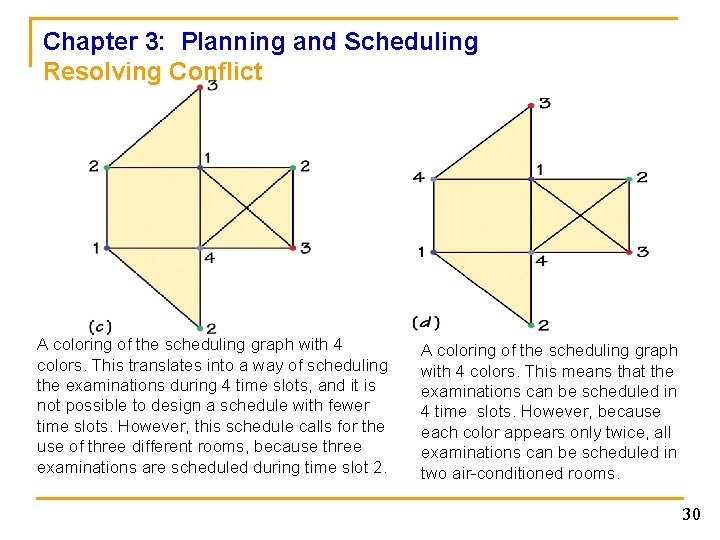
Chapter 3: Planning and Scheduling Resolving Conflict A coloring of the scheduling graph with 4 colors. This translates into a way of scheduling the examinations during 4 time slots, and it is not possible to design a schedule with fewer time slots. However, this schedule calls for the use of three different rooms, because three examinations are scheduled during time slot 2. A coloring of the scheduling graph with 4 colors. This means that the examinations can be scheduled in 4 time slots. However, because each color appears only twice, all examinations can be scheduled in two air-conditioned rooms. 30