Chapter 3 Physical Quantities are of 2 types

Chapter 3

Physical Quantities are of 2 types… A scalar is only a magnitude (length) (Example: Temperature, time, mass) A vector has magnitude and direction (Example: displacement = 10 m East, Velocity= 50 mph west)

�A vector will be symbolized by the “letter” with an arrow over it. The arrow indicates direction. �Vectors are equal if they have the same units, magnitude, and direction. �A vector can be moved anywhere parallel to itself.

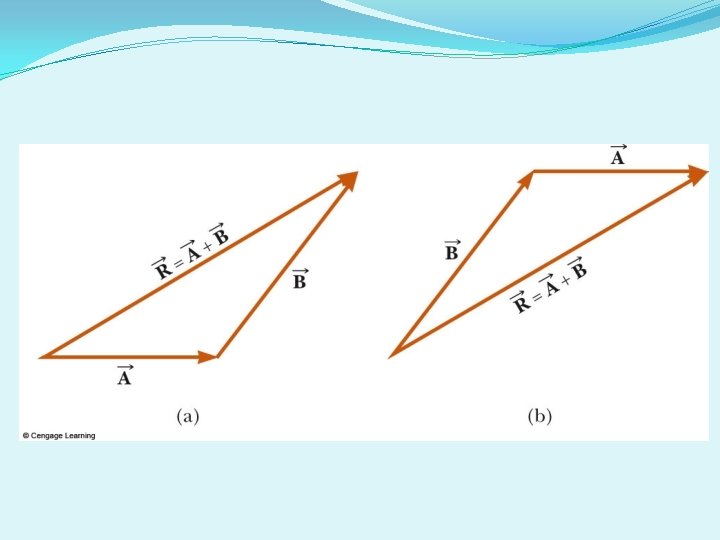
Adding Vectors (attach) To add vectors they must have the same units. Tip-to -tail method put them head to tail and connect them so you end up with a triangle. Parallelogram Method- (put them tail to tail) make vectors parallel and draw a line making 2 triangles

More Properties of Vectors Resultant Vector The resultant vector is the sum of a given set of vectors

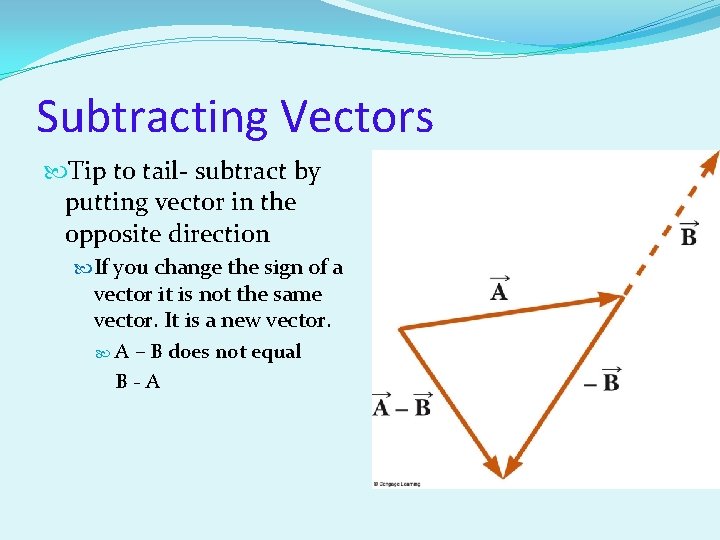
Subtracting Vectors Tip to tail- subtract by putting vector in the opposite direction If you change the sign of a vector it is not the same vector. It is a new vector. A – B does not equal B-A

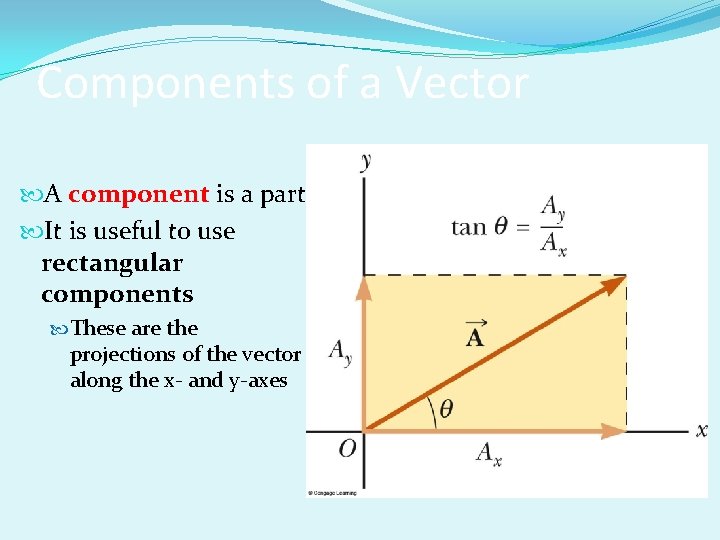
Components of a Vector A component is a part It is useful to use rectangular components These are the projections of the vector along the x- and y-axes

Components of a Vector, cont. The x-component of a vector is the projection along the x-axis The y-component of a vector is the projection along the y-axis Then,

Useful Formulas. . The Pythagorean Theorem can only be used with right triangles!

When its not 900 R 2= A 2 + B 2 – 2 AB(COSӨ)

Example 1 Find the magnitude of the sum of a 15 km displacement and a 25 km displacement when the angle between them is 900 and when the angle between them is 1350.

Example Problem (a) Find the horizontal and vertical components of the 100 m displacement of a superhero who flies from the top of a tall building at an angle of 30. 00 (b) Suppose instead the superhero leaps in the other direction along a displacement vector B to the top of a flagpole where the displacement components are given Bx = -25 m and BY=10. 0 m. Find the magnitude and direction of the displacement vector.

Example 2 A GPS receiver indicates that your home is 15. 0 km and 400 north of west, but the only path through the woods leads directly north. If you follow the path 5. 0 km before it opens into a field, how far, and in what direction, would you have to walk to reach your home? R= 12. 39 Ө= 158’

Resolving a Vector Into Components The horizontal, or x-component, of A is found by Ax = A cos q. +y Ay A q +x Ax The vertical, or y-component, of A is found by Ay = A sin q. By the Pythagorean Theorem, Ax 2 + Ay 2 = A 2. Every vector can be resolved using these formulas, such that A is the magnitude of A, and q is the angle the vector makes with the x-axis. Each component must have the proper “sign” according to the quadrant the vector terminates in.

Analytical Method of Vector Addition 1. Find the x- and y-components of each vector. Ax = A cos q = Bx = B cos q = Cx = C cos q = Ay = A sin q = By = B sin q = Cy = C sin q = Rx = Ry = 2. Sum the x-components. This is the x-component of the resultant. 3. Sum the y-components. This is the y-component of the resultant. 4. Use the Pythagorean Theorem to find the magnitude of the resultant vector. Rx 2 + Ry 2 = R 2

A roller coaster moves 215 ft horizontally and then rises 130 ft at an angle of 35. 00 above the horizontally. Next, it travels 125 ft at an angle of 50. 00 below the horizontal. Find the roller coaster’s displacement from its starting point to the end of this movement.

You try this one on your own… Add the following vectors via the component method: Vector A = 4 m South, Vector B= 7. 3 m Northwest Find R and Ө

A person walks 25. 0° north of east for 2. 80 km. How far would the person walk due north and due east to arrive at the same location? 1. 183 km North 2. 53 km East

A person walks East for 255 m and then 60° North of East for 100 m. Find the magnitude and direction of the resultant displacement.

A vector has an x-componet of -25. 0 units and a ycomponet of 45. 0 units. Find the magnitude and direction of the vector.

A quarter back takes the ball from the line of scrimmage, runs backwards for 15. 0 yards, then runs sideways parallel to the line of scrimmage for 15. 0 yards. At this point, he throws a 60. 0 yard forward pass straight downfield, perpendicular to the line of scrimmage. What is the magnitude of the football’s resultant displacement?

A Novice Golfer on the green takes three strokes to sink the ball. The successive displacement of the ball are 5. 00 m to the north, 2. 00 m 550 north of east, and 1. 00 m at 300 west of south. Starting at the same initial point, an expert golfer could make the hole in what singe displacement?

Practice Problems 3 A-3 C Problems 1 -4 (pg 89), 1 -4 (pg 92), 1 -4 pg 94

Projectile Motion

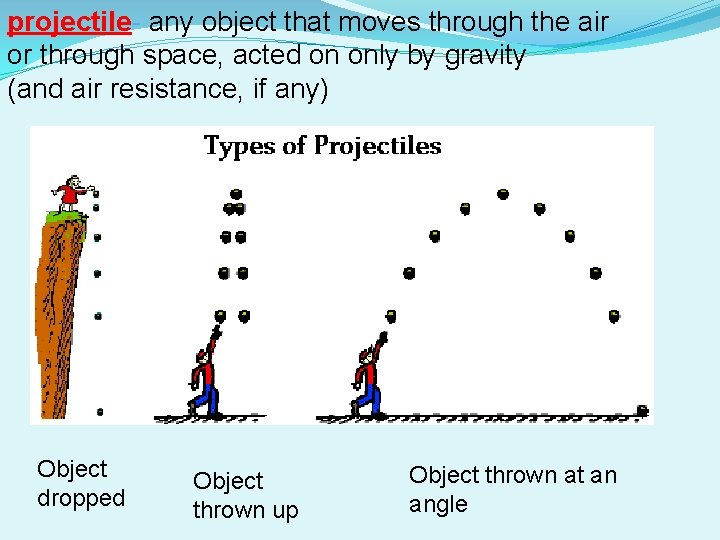
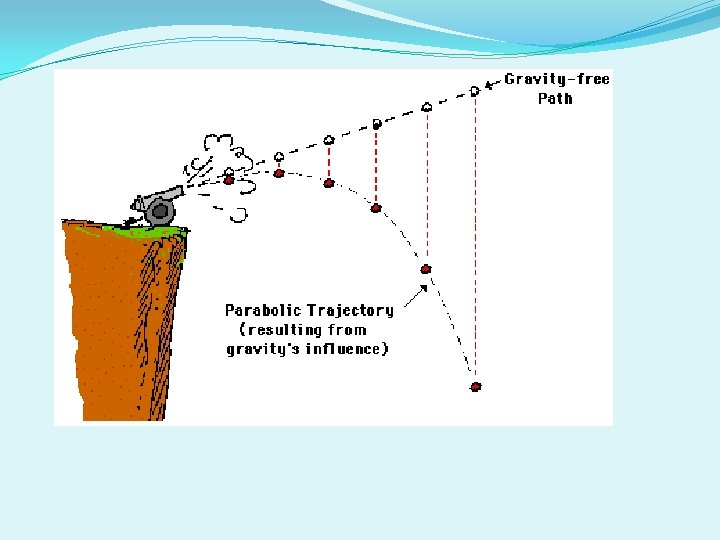
A projectile is a motion in two dimensions Moving in the x and y direction A projectile is an object shot through the air. This occurs in a parabola curve.

projectile- any object that moves through the air or through space, acted on only by gravity (and air resistance, if any) Object dropped Object thrown up Object thrown at an angle

-The vertical acceleration of a projectile is caused by gravity, so ay = -9. 8 m/s 2 Parabolic Trajectory

We assume that g remains constant (g= -9. 8 m/s 2) a in the x direction is 0 because gravity is not acting on it. Neglect air resistance Neglect the effects of the earths rotation

Projectiles launched horizontally

To find how far the ball falls, you use the formula. Y =viyt + 1/2 gt 2 1 st second- 5 m After 2 seconds- 20 m After 3 seconds- 45 m The curved path of a projectile produced is a parabola (caused by both horizontal motion and vertical motion. It must accelerate only in the vertical direction)

A projectile Motion is 2 dimensions The projectile will experience two: Accelerations (ax= o and a. Y= -9. 8 m/s 2) Velocities Displacements

Upwardly Launched Projectiles When a projectile is launched at an upward angle, it follows a curved path and finally hits the ground because of gravity. The Vertical distance a cannonball falls below “imaginary path if no gravity” is the same vertical distance it would fall if it were dropped from rest & had been falling for the same amount of time.

How to solve these problems Draw a free body diagram with a coordinate system. Divide the information into x and y components Look at your formulas and decided which one(s) to use.

Formulas for horizontal and vertical motion of a projectile (X) Horizontal xf-xi = vixt + ½ axt 2 vfx = vix + axt vfx 2 - vix 2 = 2 ax(xf-xi) (Y) Vertical yf-yi = viyt + ½ ayt 2 vfy = viy + ayt vfy 2 = viy 2 + 2 ay (yf-yi) Objects that have been thrown will have a horizontal velocity that stays the same (no horizontal acceleration ax = 0 m/s 2) So vfx =vix in the second formula and third formulas under horizontal motion.

One more formula…. This equation only works when yf and yi are both 0…. t= 2 viy a

If a ball is thrown up in the air from a moving truck, where will it land? (Ignore air resistance) In front of the truck, behind the truck, or back in the truck

Where will a package land if it is released from a plane? Behind the plane, in front of the plane below the plane

Look at the example lets try it together. A ball is launched at 4. 5 m/s at 660 above the horizontal. What are the maximum height and flight time of the ball? What is the time? Maximum height (y)? Total displacement (x)?

What is the horizontal distance covered by an arrow that was shot through the air at a 600 angle with a velocity of 55 m/s? Given 55 m/s Solve v = 55 m/s Vxi = cos 60(55 m/s)=27. 5 m/s vix=27. 5 m/s Viy = sin 60(55 m/s)=47. 6 m/s viy=47. 6 m/s To find x dist: x = v 0 x t ax=0 Need to find time first! ay=-9. 8 m/s 2 v =v +a t fy iy y t=? 0 = 47. 6 m/s + -9. 8 m/s 2 t dx=? dy 600 Vix dx dx = Vix t (we need time) dx = 27. 5 m/s(9. 7 s) dx = 266. 75 m -47. 6 m/s = -9. 8 m/st 4. 86 s =t Total time in the air 4. 86 s x 2 = 9. 7 s

Courtney kicks a soccer ball at rest on level ground giving it an initial velocity of 7. 8 m/s at an angle of 320 How long will the ball be in the air? How high will the ball go? What will be its range?

A shell is fired from a ship at an angle of 300 above the horizontal with a speed of 300 m/s. If the shell hits the ocean’s surface in 30. 6 s, calculate: (a. ) the distance traveled horizontally (b. ) the maximum height reached by the shell (c. ) the speed of the shell when it reaches its maximum height

A Titan Fan stands at the edge of the bleachers and throws a stone horizontally over the edge with a speed of 18. 0 m/s. The bleachers are 50. 0 m above a flat horizontal parking lot. (a) How long after being released does the stone strike the parking lot below the cliff? (b) What is the speed in the horizontal direction when the stone reaches the parking lot?

Peter Rowe kicks a soccer ball at rest on level ground giving it an initial velocity of 13. 0 m/s at an angle of 400. a. How long will the ball be in the air? b. How high will the ball go? c. What will be its range?

A brick is thrown upward from the top of a building at an angle of 250 to the horizontal and with an initial speed of 15 m/s. If the brick is in flight for 3. 0 s, how tall is the building?

A fireman 50. 0 m away from a burning building directs a stream of water from a ground-level fire hose at an angle of 30. 00 above the horizontal. If the speed of the stream as it leaves the hose is 40. 0 m/s, at what height will the stream of water strike the building? (hint) We have to find time first!

A stone is thrown horizontally at a speed of 5. 0 m/s from the top of a cliff that is 78. 4 m high. How long does it take the stone to reach the bottom of the cliff? How far from the base of the cliff does the stone hit the ground? What are the horizontal and vertical components of the stone’s velocity just before it hits the ground?

Lucy and her friend are working at an assembly plant making wooden toy giraffes. At the end of the line, the giraffes go horizontally off the edge of the conveyor belt and fall into a box below. If the box is 0. 6 m below the level of the conveyor belt and 0. 4 m away from it, what must be the horizontal velocity of the giraffes as they leave the conveyer belt?

A player kicks a football from ground level with an initial velocity of 27. 0 m/s, 30. 00 above the horizontal What is: The ball’s hang time? The ball’s maximum height? The ball’s range?

The player kicks the ball with the same speed, but at 600 from the horizontal. What is the balls hang time, range, and maximum height?

Practice Problems 3 D-3 E Problems 1 -4 (pg 99), 1 -4 (pg 101), 1 -4 pg 94

Relative Motion Frames of Reference Observers using different frames of reference may measure different displacements or velocities for an object in motion Relative Velocities the difference between the velocities relative to some common point

Relative Motion: Suppose you are on a train platform as the train rushes through the station without stopping. Someone on board the train is pitching a ball, throwing it has hard as they can towards the back of the train. If the train’s speed is 60 mph and the pitcher is capable of throwing at 60 mph, what is the speed of the ball as you see it from the platform?

Relative Motion Moving frame of reference A boat heading due north crosses a river with a speed of 10. 0 km/h. The water in the river has a speed of 5. 0 km/h due east. In general we have (a) Determine the velocity of the boat. (b) If the river is 3. 0 km wide how long does it take to cross it?

Practice Problems 3 F Problems 1 -4 (pg 105 Mixed Review 47 -62 (pgs 111 -113