Chapter 3 Numeration Systems and Whole Number Operations

Chapter 3 Numeration Systems and Whole Number Operations Copyright © 2016, 2013, and 2010, Pearson Education, Inc.

3 -4 Addition and Subtraction Algorithms, Mental Computation, and Estimation • Models to develop algorithms for addition and subtraction. • Addition and subtraction algorithms including the standard algorithms and how to use them to solve problems. • Number bases other than ten to provide insight into base-ten algorithms. • Mental addition and subtraction computational skills and estimation techniques to check reasonableness of answers. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 2
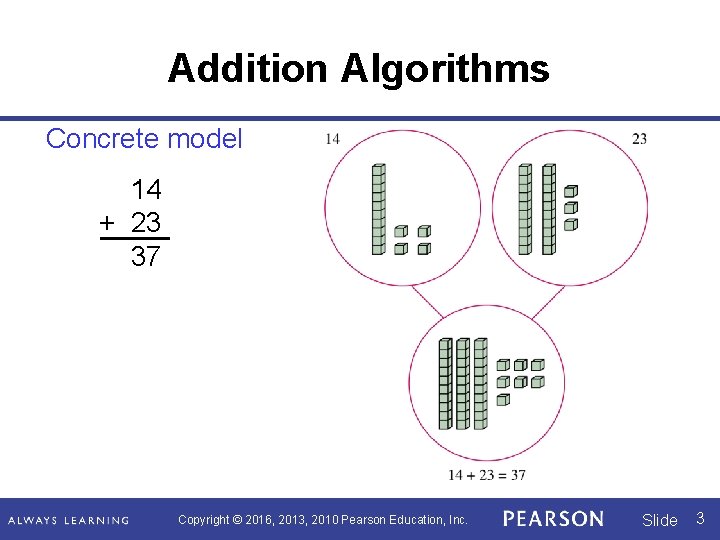
Addition Algorithms Concrete model 14 + 23 37 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 3

Addition Algorithms Expanded algorithm 14 +23 7 +30 37 Standard algorithm (Add ones) (Add tens) 14 +23 37 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 4

Addition Algorithms Expanded algorithm with regrouping 37 +28 15 +50 65 (Add ones) (Add tens) Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 5

Addition Algorithms Standard algorithm with regrouping 1 37 +28 65 (Add ones, regroup, and add the tens) Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 6

Addition Algorithms Add two three-digit numbers with two regroupings. 186 + 127 Add the ones and regroup. 6 ones + 7 ones = 13 ones = 1 ten + 3 ones 1 186 + 127 3 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 7

Addition Algorithms Add two three-digit numbers with two regroupings. 186 + 127 Add the tens and regroup. 1 ten + 8 tens + 2 tens = 11 tens = 1 hundred + 1 ten (continued) 11 186 + 127 13 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 8

Addition Algorithms Add two three-digit numbers with two regroupings. (continued) 186 + 127 Add the hundreds. 1 hundred + 1 hundred = 3 hundreds 11 186 + 127 313 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 9

Addition Algorithms Left-to-Right Algorithm for Addition (Partial Sums) 568 + 757 (500 + 700)→ 1200 (60 + 50) → 110 (8 + 7) → 15 1325 → 568 + 757 1215 → 1325 32 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 10

Addition Algorithms Lattice Algorithm for Addition Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 11

Addition Algorithms Scratch Algorithm for Addition 87 65 2 + 49 Add the numbers in the units place starting at the top. When the sum is 10 or more, record this sum by scratching a line through the last digit added and writing the number of units next to the scratched digit. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 12

Addition Algorithms Scratch Algorithm for Addition (continued) 87 65 2 + 49 1 Continue adding the units, including any new digits written down. When the addition again results in a sum of 10 or more, repeat the process. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 13

Addition Algorithms Scratch Algorithm for Addition (continued) 2 87 65 2 + 49 1 1 When the first column of additions is completed, write the number of units, 1, below the addition line in the proper place value position. Count the number of scratches, 2, and add this number to the second column. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 14

Addition Algorithms Scratch Algorithm for Addition (continued) 2 80 7 6 52 + 40 9 1 2 0 1 Repeat the procedure for each successive column until the last column with non-zero values. At this stage, sum the scratches and place the number to the left of the current value. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 15

Subtraction Algorithms Concrete model 243 − 61 Represent 243 with 2 flats, 4 longs, and 3 units, as shown. To subtract 61 from 243, we try to remove 6 longs and 1 unit from the blocks shown in the figure. We can remove 1 unit, but to remove 6 longs, we have to trade 1 flat for 10 longs. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 16

Subtraction Algorithms Concrete model (continued) Now we can remove, or “take away, ” 6 longs and 1 unit, leaving 1 flat, 8 longs, and 2 units, or 182. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 17

Subtraction Algorithms Concrete model (continued) 243 − 61 182 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 18

Equal-Addends Algorithm The equal-additions algorithm for subtraction is based on the fact that the difference between two numbers does not change if we add the same amount to both numbers. 255 + 7 262 + 30 292 → → − 163 + 7 − 170 − (170 + 30) − 200 92 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 19

Understanding Addition and Subtraction in Bases Other Than Ten 343 five + 2 five = 400 five 222 five – 43 five = 124 five Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 20

Understanding Addition and Subtraction in Bases Other Than Ten Concrete model 12 five + 31 five 43 five Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 21

Understanding Addition and Subtraction in Bases Other Than Ten Expanded algorithm 12 five + 31 five 3 + 40 43 five Standard algorithm 12 five + 31 five 43 five Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 22

Understanding Addition and Subtraction in Bases Other Than Ten Fives 3 − 1 Ones 2 4 → Fives 2 − 1 1 Ones 12 4 3 Copyright © 2016, 2013, 2010 Pearson Education, Inc. 21 32 five − 14 five 13 five Slide 23

Mental Mathematics and Estimation for Whole-Number Operations Mental mathematics The process of producing an answer to a computation without using computational aids. Computational estimation The process of forming an approximate answer to a numerical problem. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 24

Mental Mathematics: Addition 1. Adding from the left 76 + 25 70 + 20 = 90(Add the tens. ) 6 + 5 = 11 (Add the ones. ) 90 + 11 = 101 (Add the two sums. ) 2. Breaking up and bridging 76 + 25 76 + 20 = 96 96 + 5 = 101 Add the first number to the tens in the second number. Add the sum to the units in the second number. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 25

Mental Mathematics: Addition 3. Trading off 76 → 76 + 4 = 80 Add 4 to make a multiple of 10. + 25 → 25 – 4 = 21 Subtract 4 to compensate. 80 + 21 = 101 Add the two numbers. 4. Using compatible numbers Compatible numbers are numbers whose sums are easy to calculate mentally. 130 + 50 + 70 + 20 + 50 = 200 + 100 + 20 = 320 200 100 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 26

Mental Mathematics: Addition 5. Making compatible numbers 76 → 75 + 25 = 100 + 25 → 100 + 1 = 101 75 + 25 adds to 100. Add 1 more unit. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 27

Mental Mathematics: Subtraction 1. Breaking up and bridging 74 → 74 – 20 = 54 – 26 → 54 – 6 = 48 2. Trading off 74 → – 26 → 3. Drop the zeros 74 + 4 = 78 26 + 4 = 30 78 – 30 = 48 7400 → 74 – 6 = 68 – 600 → 7400 – 600 = 6800 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 28

Example Noah owed $11 for his groceries. He used a $50 bill to pay. While handing Noah the change, the cashier said, “ 11, 12, 13, 14, 15, 20, 30, 50. ” How much change did Noah receive? What the cashier said $11 $12 $13 $14 Amount of money Noah received 0 $1 $15 $20 $30 $50 $1 $5 Copyright © 2016, 2013, 2010 Pearson Education, Inc. $10 $20 Slide 29

Example (continued) The total amount of change that Noah received is $1 + $5 + $10 + $20 = $39 Thus $50 − $11 = $39 because $39 + $11 = $50. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 30
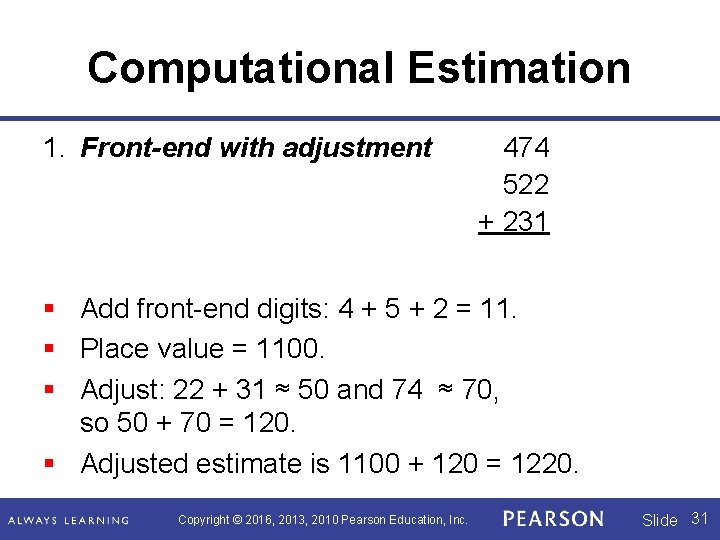
Computational Estimation 1. Front-end with adjustment 474 522 + 231 § Add front-end digits: 4 + 5 + 2 = 11. § Place value = 1100. § Adjust: 22 + 31 ≈ 50 and 74 ≈ 70, so 50 + 70 = 120. § Adjusted estimate is 1100 + 120 = 1220. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 31

Computational Estimation 2. Grouping to nice numbers About 100 23 39 32 64 + 49 About 100 The sum is about 200. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 32

Computational Estimation 3. Clustering Used when a group of numbers cluster around a common value § Estimate the “average”: about 5000 § Multiply the “average” by the number of values: 5 5000 = 25, 000 Copyright © 2016, 2013, 2010 Pearson Education, Inc. 4724 5262 5206 4992 + 5331 Slide 33

Computational Estimation 4. Rounding 7262 → 7000 – 3806 → – 4000 3000 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 34
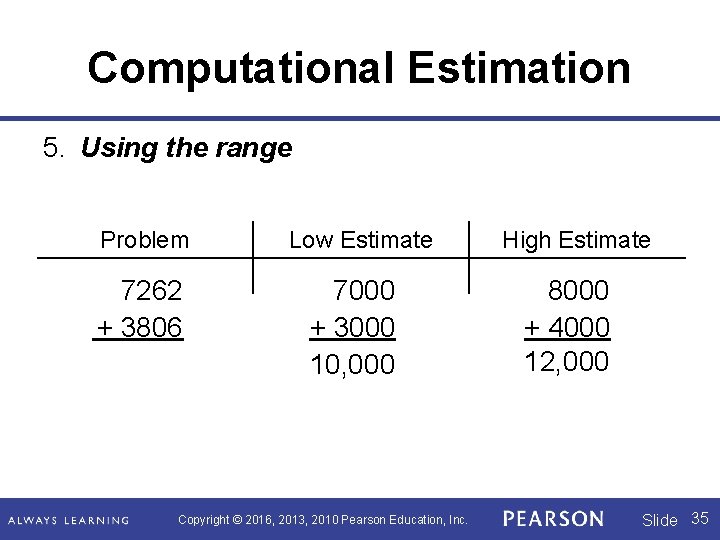
Computational Estimation 5. Using the range Problem 7262 + 3806 Low Estimate 7000 + 3000 10, 000 Copyright © 2016, 2013, 2010 Pearson Education, Inc. High Estimate 8000 + 4000 12, 000 Slide 35
- Slides: 35