Chapter 3 Multivariate Random Variables 3 1 TwoDimensional

Chapter 3 Multivariate Random Variables

3. 1 Two-Dimensional Random Variables 1. n-dimensional variables n random variables X 1，X 2，. . . , Xn compose a ndimensional vector (X 1, X 2, . . . , Xn), and the vector is named n-dimensional variables or random vector. 2. Joint distribution of random vector Define function F(x 1, x 2, …xn)= P(X 1≤x 1, X 2 ≤ x 2, . . . , Xn ≤ xn) the joint distribution function of random vector (X 1, X 2, . . . , Xn).

The Joint cdf for Two random variables Definition 3. 1 -P 53 Let (X, Y) be 2 -dimensional random variables. Define F(x, y)=P{X x, Y y} the bivariate cdf of (X, Y). Geometric interpretation： the value of F( x, y) assume the probability that the random points belong to area in dark

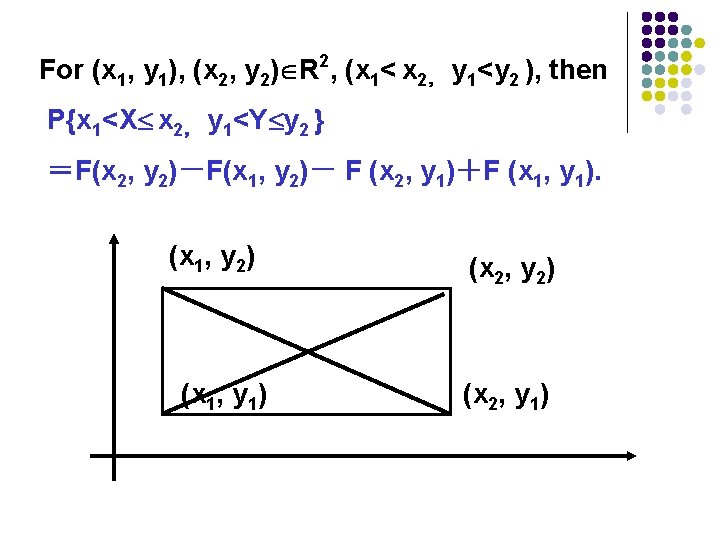
For (x 1, y 1), (x 2, y 2) R 2, (x 1< x 2， y 1<y 2 ), then P{x 1<X x 2， y 1<Y y 2 } ＝F(x 2, y 2)－F(x 1, y 2)－ F (x 2, y 1)＋F (x 1, y 1). (x 1, y 2) (x 1, y 1) (x 2, y 2) (x 2, y 1)

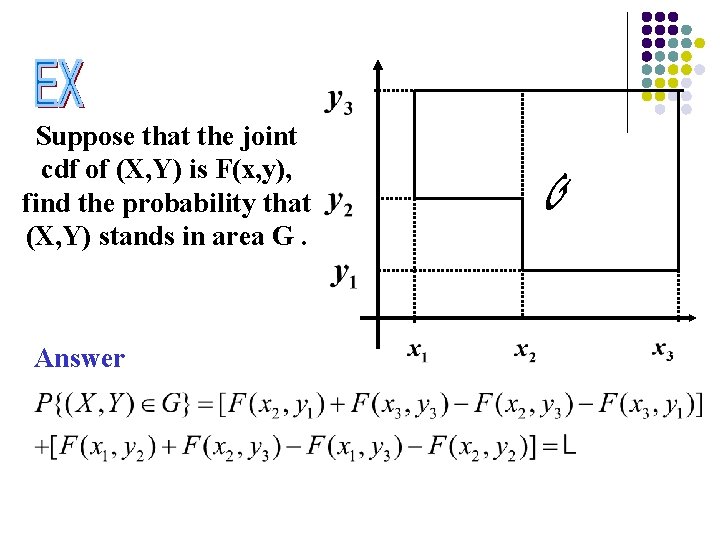
Suppose that the joint cdf of (X, Y) is F(x, y), find the probability that (X, Y) stands in area G. Answer

Joint distribution F(x, y) has the following characteristics: (1) For all (x, y) R 2 , 0 F(x, y) 1,

(2) Monotonically increment for any fixed y R, x 1<x 2 yields F(x 1, y) F(x 2 , y)； for any fixed x R, y 1<y 2 yields F(x, y 1) F(x , y 2). (3) right continuous for x R, y R,

(4) for all (x 1, y 1), (x 2, y 2) R 2, (x 1< x 2， y 1<y 2 ), F(x 2, y 2)－F(x 1, y 2)－ F (x 2, y 1)＋F (x 1, y 1) 0. Conversely, any real-valued function satisfied the aforementioned 4 characteristics must be a joint distribution function of 2 -dimensional variables.

Example 1. Let the joint distribution of (X, Y) is 1) Find the value of A，B，C。 2) Find P{0<X<2, 0<Y<3} Answer

Discrete joint distribution If both x and y are discrete random variable, then, (X, Y) take values in (xi, yj), (i, j＝ 1, 2, … ), it is said that X and Y have a discrete joint distribution. Definition 3. 2 -P 54 The joint distribution is defined to be a function such that for any points (xi, yj), P{X＝xi, Y＝ yj, }＝ pij ， (i, j＝ 1, 2, … ). That is (X, Y)～ P{X＝xi, Y＝ yj, }＝ pij ，(i, j＝ 1, 2, … )，

The joint distribution can also be specified in the following table Y y 1 y 2 x 1 p 12 . . . P 1 j. . . x 2 p 21 p 22 . . . P 2 j. . . X Pij. . . Characteristics of joint distribution : (1) pij 0 , i, j＝ 1, 2, … ； (2) yj … . . . pi 2. . . pi 1 . . . xi …

Example 2. Suppose that there are two red balls and three white balls in a bag, catch one ball from the bag twice without put back, and define X and Y as follows: Please find the joint pmf of (X, Y) X Y 1 0

Continuous joint distributions and density functions 1. It is said that two random variables (X, Y) have a continuous joint distribution if there exists a nonnegative function f (x, y) such that for all (x, y) R 2， the distribution function satisfies and denote it with (X, Y)～ f (x, y)， (x, y) R 2

2. characteristics of f(x, y) (1) f (x, y) 0, (x, y) R 2; (2) (3) (4) For any region G R 2,

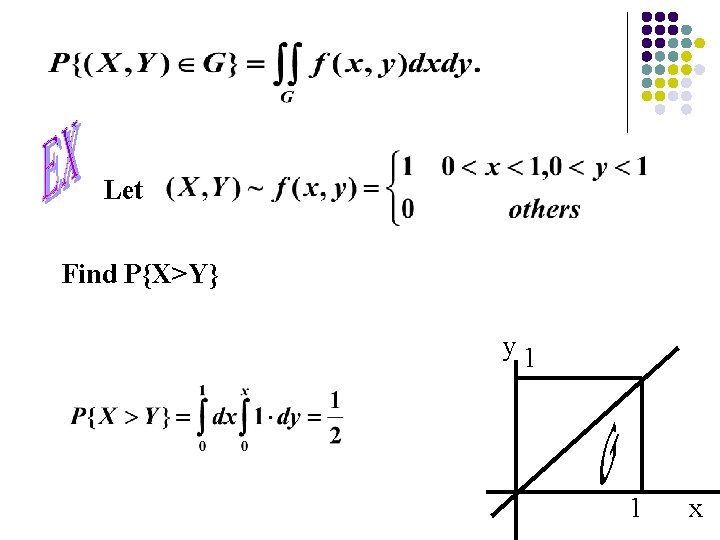
Let Find P{X>Y} y 1 1 x

Find (1)the value of A； (2) the value of F(1, 1)； (3) the probability of (X, Y) stand in region D：x 0, y 0, 2 X+3 y 6 1 Answer (1) Since 1