Chapter 3 Motion in a Plane Vector Addition







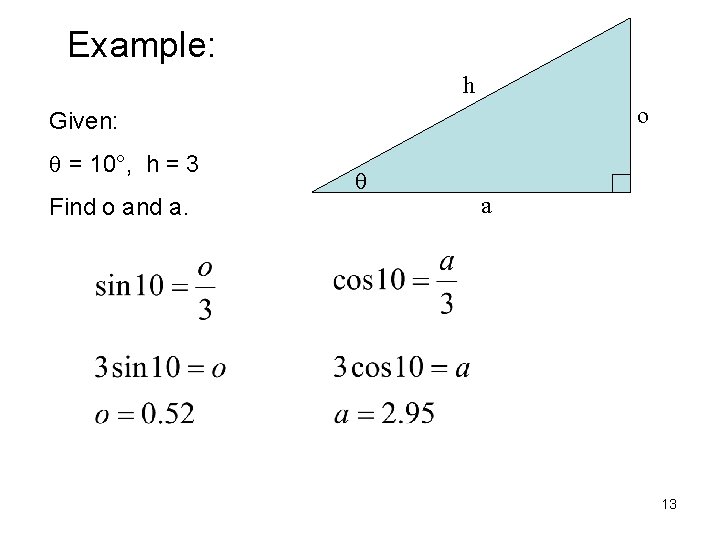








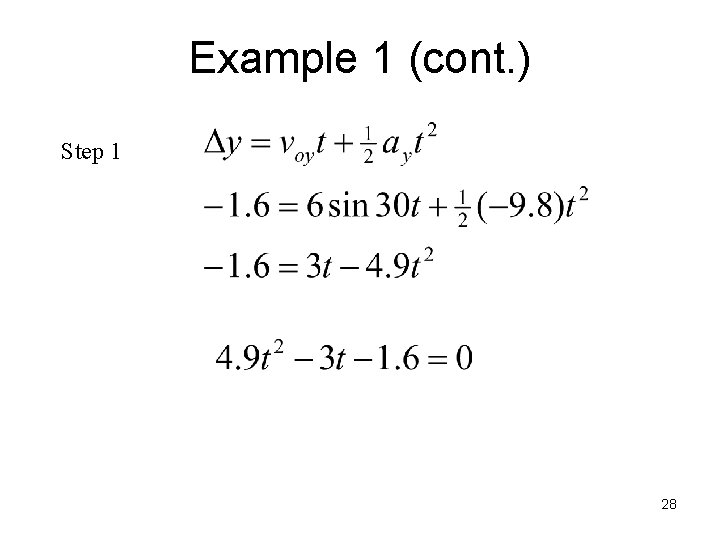




















- Slides: 52

Chapter 3: Motion in a Plane • • Vector Addition Velocity Acceleration Projectile motion Relative Velocity CQ: 1, 2. P: 3, 5, 7, 13, 21, 39, 49, 51.

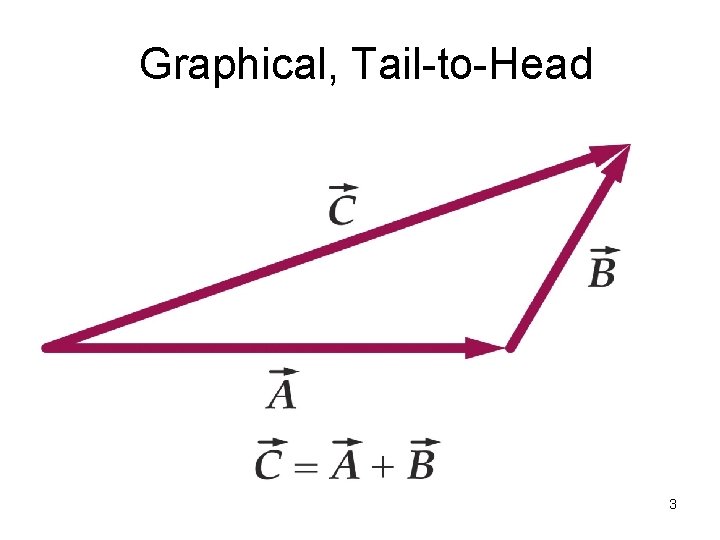
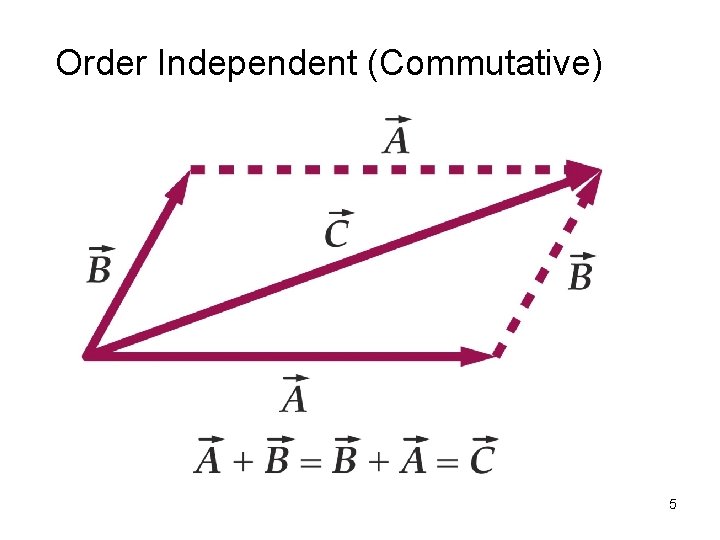
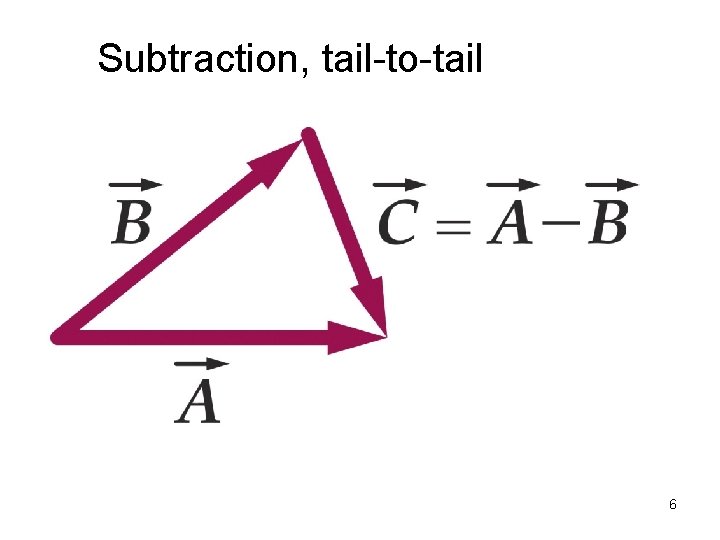
Two Dimensional Vectors • Displacement, velocity, and acceleration each have (x, y) components • Two methods used: • geometrical (graphical) method • algebraic (analytical) method • / 2

Graphical, Tail-to-Head 3

Addition Example • Giam (11)

Order Independent (Commutative) 5

Subtraction, tail-to-tail 6

Subtraction Example • Giam (19)

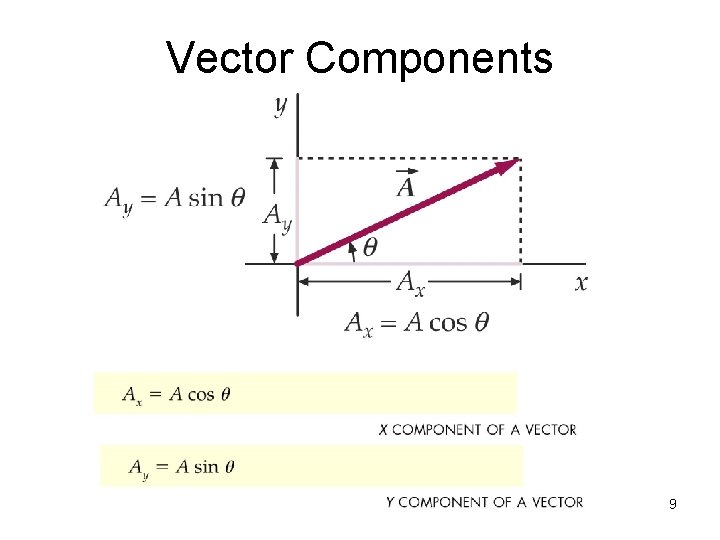
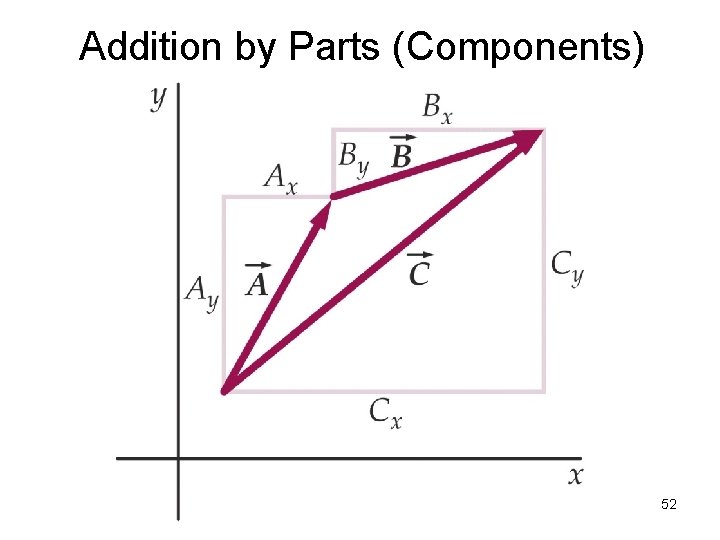
Algebraic Component Addition • trigonometry & geometry • “R” denotes “resultant” sum • Rx = sum of x-parts of each vector • Ry = sum of y-parts of each vector 8

Vector Components 9

Examples • Magnitude || (g 4 -5) Notation, Example • Component Example Animated • Phet Vectors 10

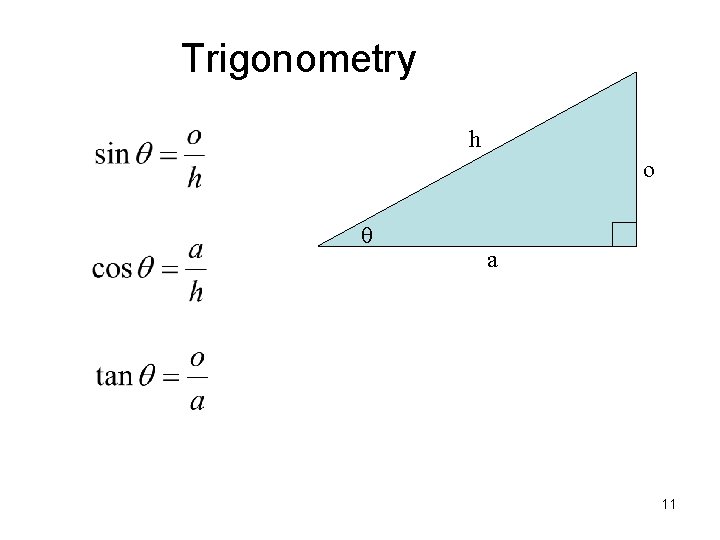
Trigonometry h o q a 11

Using your Calculator: Degrees and Radians Check this to verify your calculator is working with degrees 12
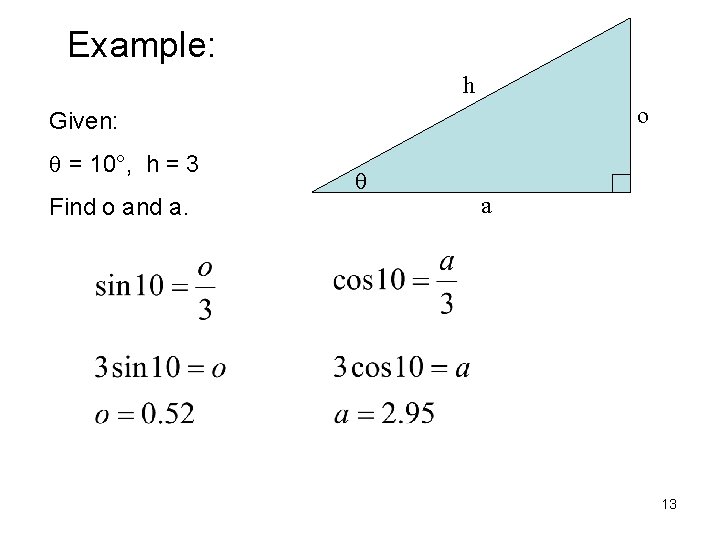
Example: h o Given: q = 10°, h = 3 Find o and a. q a 13

Inverse Trig • Determine angle from length ratios. • Ex. o/h = 0. 5: • Ex. o/a = 1. 0: 14

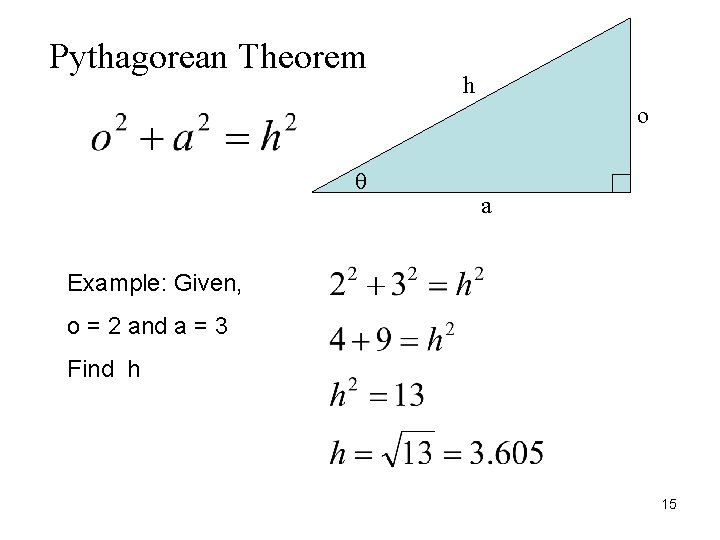
Pythagorean Theorem h o q a Example: Given, o = 2 and a = 3 Find h 15

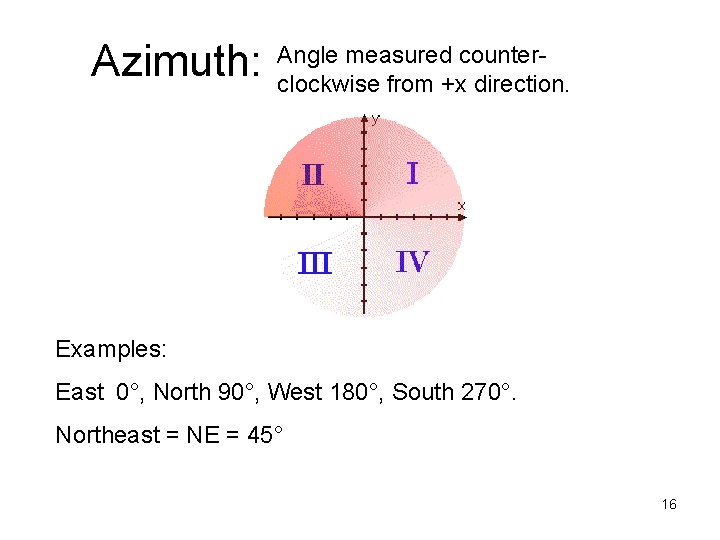
Azimuth: Angle measured counterclockwise from +x direction. Examples: East 0°, North 90°, West 180°, South 270°. Northeast = NE = 45° 16

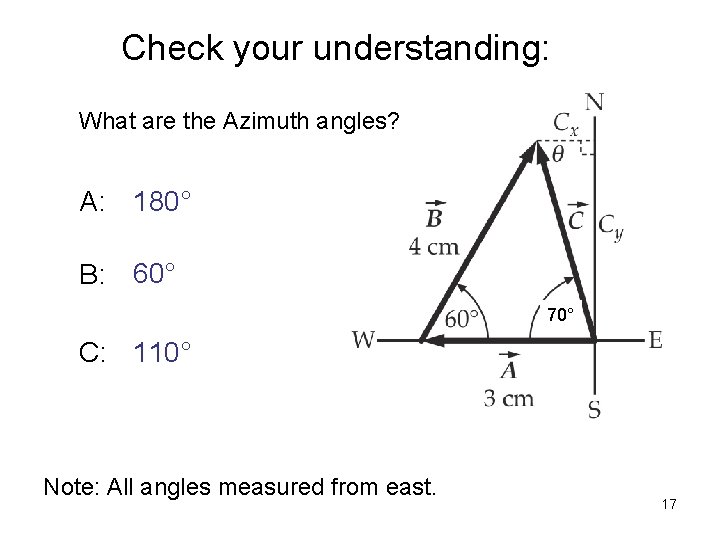
Check your understanding: What are the Azimuth angles? A: 180° B: 60° 70° C: 110° Note: All angles measured from east. 17

Components: Given A = 2. 0 m @ 25°, its x, y components are: Check using Pythagorean Theorem: 18

Vector Addition by Components: 19

Example Vector Addition R = (10 cm, 0°) + (10 cm, 45°): 20

(cont) Magnitude, Angle: 21

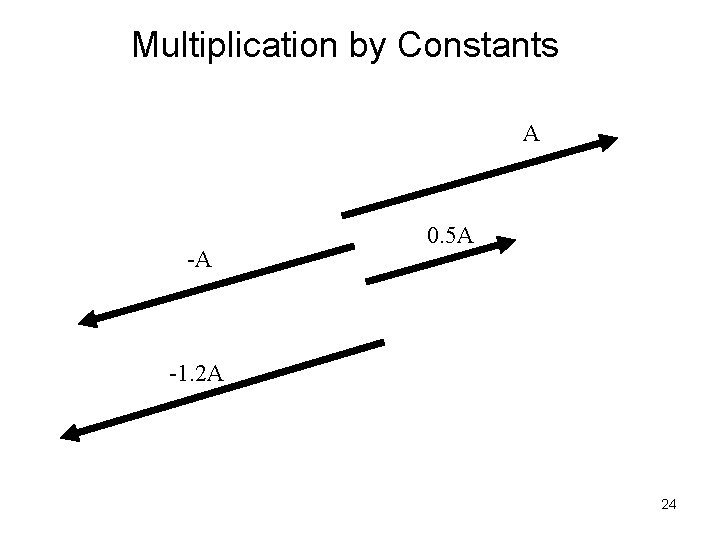
General Properties of Vectors • size and direction define a vector • location independent • change size and/or direction when multiplied by a constant • Vector multiplied by a negative number changes to a direction opposite of its original direction. • written: Bold or Arrow 22

these vectors are all the same 23

Multiplication by Constants A -A 0. 5 A -1. 2 A 24

Projectile Motion • • time = 0: e. g. baseball leaves fingertips time = t: e. g. baseball hits glove Horizontal acceleration = 0 Vertical acceleration = -9. 8 m/s/s Horizontal Displacement (Range) = Dx Vertical Displacement = Dy Vo = launch speed qo = launch angle

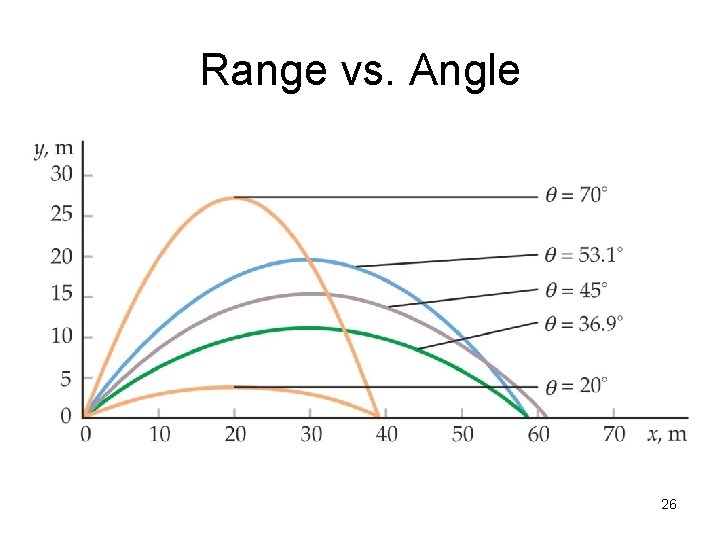
Range vs. Angle 26

Example 1: 6 m/s at 30 vo = 6. 00 m/s qo = 30° xo = 0, yo = 1. 6 m; x = R, y = 0 27
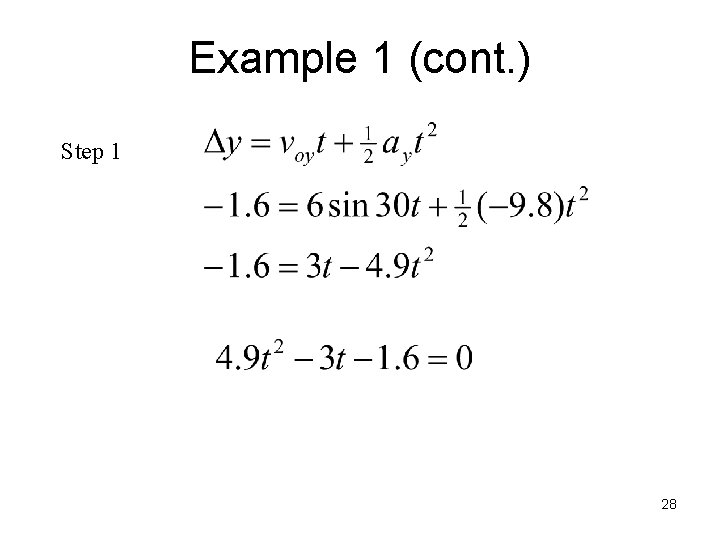
Example 1 (cont. ) Step 1 28

Quadratic Equation 29

Example 1 (cont. ) End of Step 1 30

Example 1 (cont. ) Step 2 (ax = 0) “Range” = 4. 96 m End of Example 31

Relative Motion • • • Examples: people-mover at airport airplane flying in wind passing velocity (difference in velocities) notation used: velocity “BA” = velocity of B – velocity of A 32

Summary • • Vector Components & Addition using trig Graphical Vector Addition & Azimuths Projectile Motion Relative Motion 33

R = (2. 0 m, 25°) + (3. 0 m, 50°): 34

(cont) Magnitude, Angle: 35

PM Example 2: vo = 6. 00 m/s qo = 0° xo = 0, yo = 1. 6 m; x = R, y = 0 36

PM Example 2 (cont. ) Step 1 37

PM Example 2 (cont. ) Step 2 (ax = 0) “Range” = 3. 43 m End of Step 2 38

PM Example 2: Speed at Impact 39

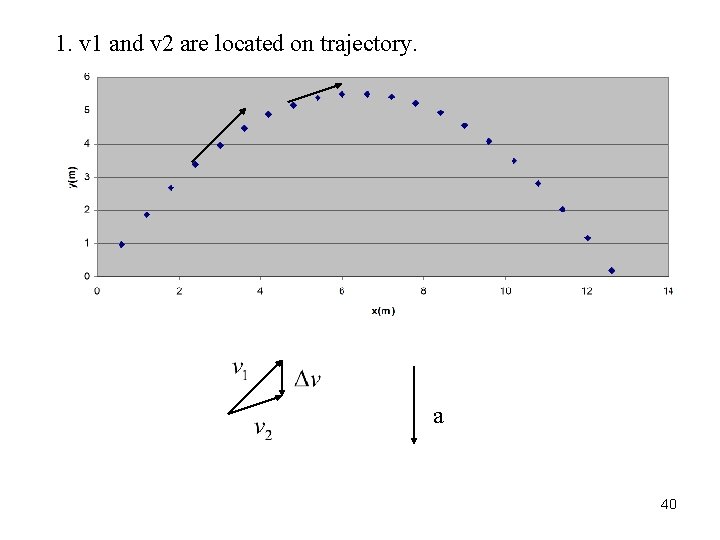
1. v 1 and v 2 are located on trajectory. v 1 a 40

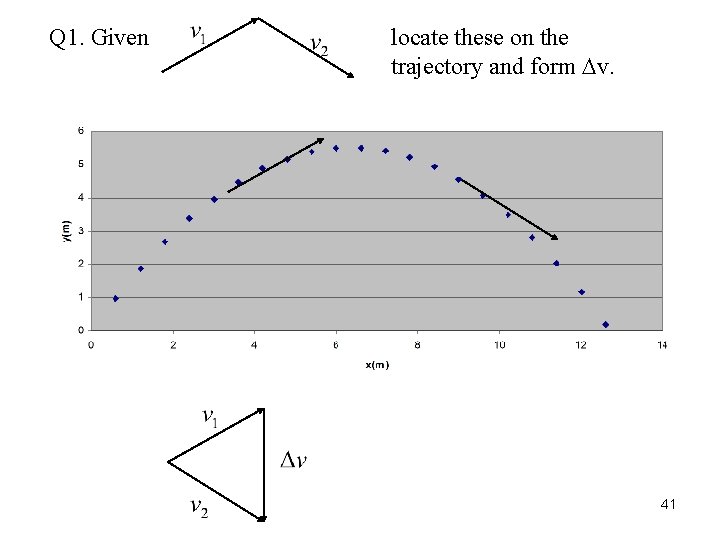
Q 1. Given locate these on the trajectory and form Dv. 41

Kinematic Equations in Two Dimensions * many books assume that xo and yo are both zero. 42

Velocity in Two Dimensions • vavg // Dr • instantaneous “v” is limit of “vavg” as Dt 0 43

Acceleration in Two Dimensions • aavg // Dv • instantaneous “a” is limit of “aavg” as Dt 0 44

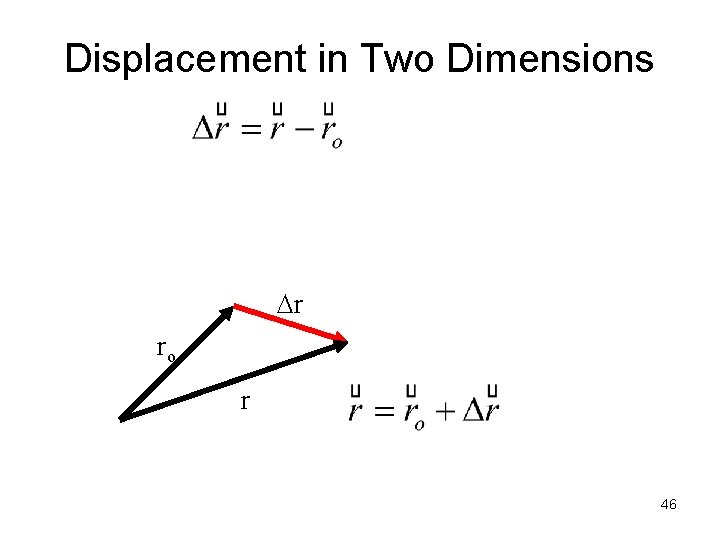
Conventions • ro = “initial” position at t = 0 • r = “final” position at time t. 45

Displacement in Two Dimensions Dr ro r 46

Acceleration ~ v change • 1 dim. example: car starting, stopping 47

Acceleration, Dv, in Two Dimensions 48

Ex. Vector Addition • Add A = 3@60 degrees azimuth, plus B = 3@300 degrees azimuth. • Find length of A+B, and its azimuth. Sketch the situation.

Ex. 2: • 10 cm@10 degrees + 10 cm@30 degrees • Length and azimuth?

Calculate F 3 • • F 1 = 8@60, F 2 = 5. 5@-45 F 1 + F 2 + F 3 = 0 F 3 = -(F 1 + F 2) Rx = 8 cos 60+5. 5 cos(-45)=7. 89 Ry = 8 sin 60+5. 5 sin(-45)=3. 04 R = 8. 46 Angle = tan-1(3. 04/7. 89) = 21 deg above +x axis Answer book wants is 180 off this angle!

Addition by Parts (Components) 52