Chapter 3 Marginal Analysis for Optimal Decisions 2016

Chapter 3 Marginal Analysis for Optimal Decisions © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 1 -1

Learning Objectives v Define several key concepts and terminology related to marginal analysis v Use marginal analysis to find optimal activity levels in unconstrained maximization problems and explain why sunk costs, fixed costs, and average costs are irrelevant for decision making v Employ marginal analysis to find the optimal levels of two or more activities in constrained maximization and minimization problems © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -2

Optimization v An optimization problem involves the specification of three things: ~ Objective function to be maximized or minimized ~ Activities or choice variables that determine the value of the objective function ~ Any constraints that may restrict the values of the choice variables © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -3

Optimization v Maximization problem ~ An optimization problem that involves maximizing the objective function v Minimization problem ~ An optimization problem that involves minimizing the objective function © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -4

Optimization v Unconstrained optimization ~ An optimization problem in which the decision maker can choose the level of activity from an unrestricted set of values v Constrained optimization ~ An optimization problem in which the decision maker chooses values for the choice variables from a restricted set of values © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -5

Choice Variables v Activities or choice variables determine the value of the objective function v Discrete choice variables ~ Can only take specific integer values v Continuous choice variables ~ Can take any value between two end points © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -6

Marginal Analysis v Analytical techniques for solving optimization problems that involves changing values of choice variables by small amounts to see if the objective function can be further improved © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -7

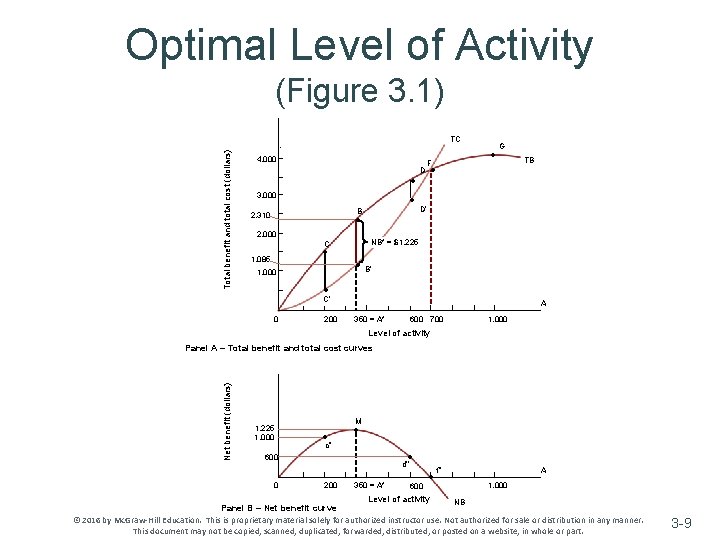
Net Benefit v Net Benefit (NB) ~ Difference between total benefit (TB) and total cost (TC) for the activity ~ NB = TB – TC v Optimal level of the activity (A*) is the level that maximizes net benefit © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -8

Optimal Level of Activity (Figure 3. 1) Total benefit and total cost (dollars) TC 4, 000 D B 2, 310 • 2, 000 1, 085 1, 000 • G • B’ • C’ 0 200 TB NB* = $1, 225 C • F • • D’ 3, 000 • A 350 = A* 600 700 1, 000 Level of activity Net benefit (dollars) Panel A – Total benefit and total cost curves 1, 225 1, 000 M • c’’ • • 600 0 d’’ 200 350 = A* • 600 Level of activity A f’’ 1, 000 NB Panel B – Net benefit curve © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -9

Marginal Benefit & Marginal Cost v Marginal benefit (MB) ~ Change in total benefit (TB) caused by an incremental change in the level of the activity v Marginal cost (MC) ~ Change in total cost (TC) caused by an incremental change in the level of the activity © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -10

Marginal Benefit & Marginal Cost © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -11

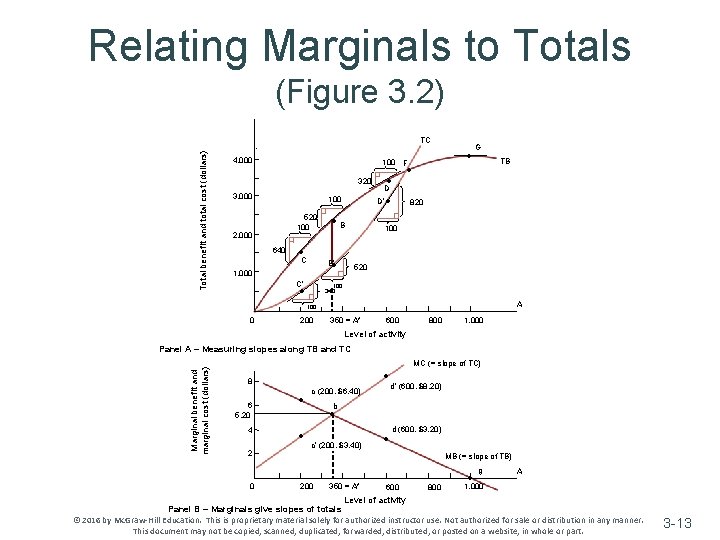
Relating Marginals to Totals v Marginal variables measure rates of change in corresponding total variables ~ Marginal benefit (marginal cost) of a unit of activity can be measured by the slope of the line tangent to the total benefit (total cost) curve at that point of activity © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -12

Relating Marginals to Totals (Figure 3. 2) Total benefit and total cost (dollars) TC 4, 000 • 100 F 320 3, 000 100 520 100 2, 000 640 • C • B • B’ 1, 000 C’ • • D’ • • G TB D 820 100 520 100 340 A 100 0 200 350 = A* 600 800 1, 000 Level of activity Marginal benefit and marginal cost (dollars) Panel A – Measuring slopes along TB and TC MC (= slope of TC) 8 6 5. 20 4 2 • • c (200, $6. 40) • d’ (600, $8. 20) b • c’ (200, $3. 40) • d (600, $3. 20) MB (= slope of TB) g 0 200 350 = A* 600 800 • 1, 000 A Level of activity Panel B – Marginals give slopes of totals © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -13

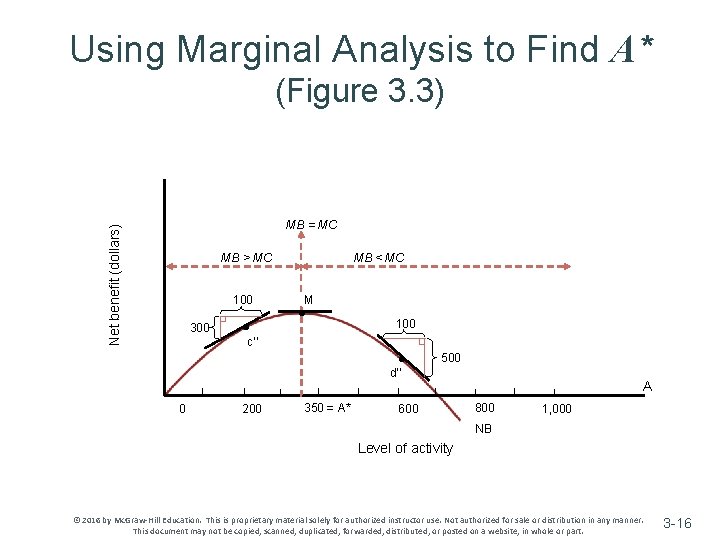
Using Marginal Analysis to Find Optimal Activity Levels v If marginal benefit > marginal cost ~ Activity should be increased to reach highest net benefit v If marginal cost > marginal benefit ~ Activity should be decreased to reach highest net benefit © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -14

Using Marginal Analysis to Find Optimal Activity Levels v Optimal level of activity ~ When no further increases in net benefit are possible ~ Occurs when MB = MC © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -15

Using Marginal Analysis to Find A* (Figure 3. 3) Net benefit (dollars) MB = MC MB > MC 100 300 0 • c’’ 200 MB < MC M • 100 • d’’ 350 = A* 500 600 A 800 1, 000 NB Level of activity © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -16

Unconstrained Maximization with Discrete Choice Variables v Increase activity if MB > MC v Decrease activity if MB < MC v Optimal level of activity ~ Last level for which MB exceeds MC © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -17

Irrelevance of Sunk, Fixed, and Average Costs v Sunk costs ~ Previously paid & cannot be recovered v Fixed costs ~ Constant & must be paid no matter the level of activity v Average (or unit) costs ~ Computed by dividing total cost by the number of units of activity © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -18

Irrelevance of Sunk, Fixed, and Average Costs v Decision makers wishing to maximize the net benefit of an activity should ignore these costs, because none of these costs affect the marginal cost of the activity and so are irrelevant for optimal decisions © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -19

Constrained Optimization v The ratio MB/P represents the additional benefit per additional dollar spent on the activity v Ratios of marginal benefits to prices of various activities are used to allocate a fixed number of dollars among activities © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -20

Constrained Optimization v To maximize or minimize an objective function subject to a constraint ~ Ratios of the marginal benefit to price must be equal for all activities ~ Constraint must be met © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -21

Summary v Marginal analysis is an analytical technique for solving optimization problems by changing the value of a choice variable by a small amount to see if the objective function can be further improved v The optimal level of the activity (A*) is that which maximizes net benefit, and occurs where marginal benefit equals marginal cost (MB = MC) ~ Sunk costs have previously been paid and cannot be recovered; Fixed costs are constant and must be paid no matter the level of activity; Average (or unit) cost is the cost per unit of activity; these 3 types of costs are irrelevant for optimal decision making v The ratio MB/P denotes the additional benefit of that activity per additional dollar spent (“bang per buck”) © 2016 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. 3 -22