Chapter 3 Linear Systems Sections 3 1 and
















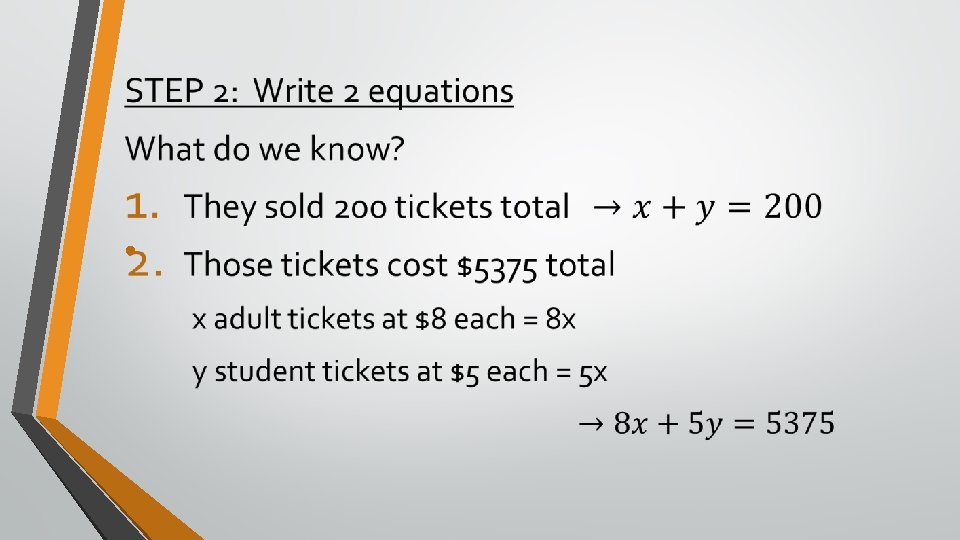









- Slides: 28

Chapter 3 – Linear Systems Sections 3. 1 and 3. 2: Solving 2 -Variable Systems

Solving Systems Using Tables and Graphs Section 3. 1

System of Equations •

Solution of a System •

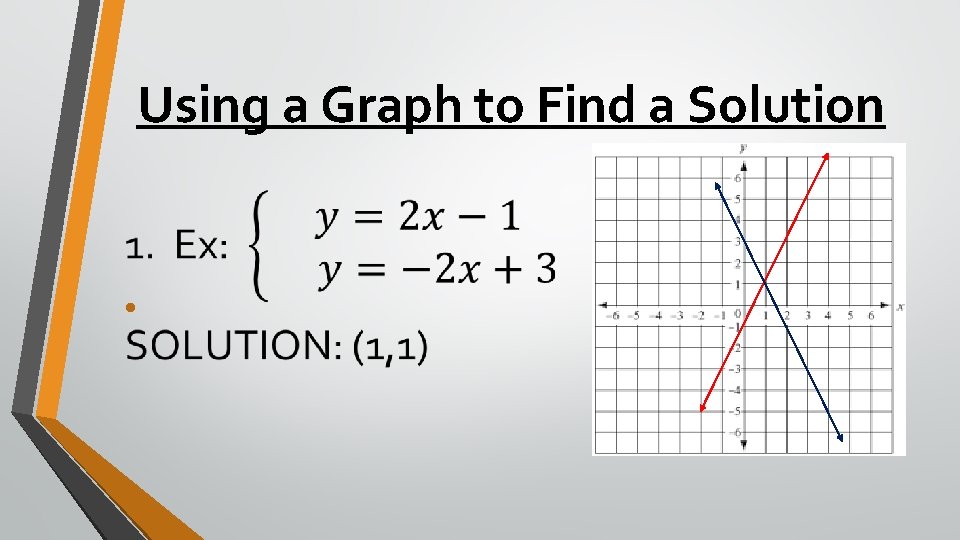
Using a Graph to Find a Solution •

STEPS 1. Solve each equation for y. 2. Carefully graph each equation with a STRAIGHT line. 3. Find the point of intersection (x, y).

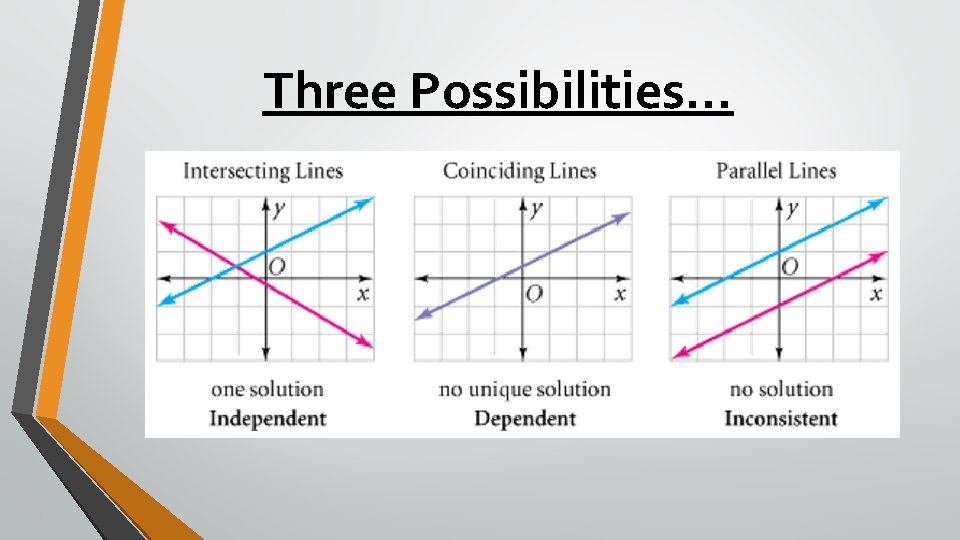
Three Possibilities…

How Can You Tell Without Graphing? 1. Solve each equation for y. 2. Compare the slopes. If they are DIFFERENT… Øthe lines will intersect ØONE SOLUTION INDEPENDENT

3. If the slopes are the same, compare the y-intercepts. If those are DIFFERENT… Øthe lines are parallel ØNO SOLUTION INCONSISTENT 4. If BOTH slope and intercepts are the same… Øthe lines coincide ØINFINITELY MANY SOLUTIONS DEPENDENT

Example •

In the Graphing Calculator • Put the two equations into Y 1 and Y 2. • They MUST be solved for y! • [2 nd][CALC][5] for intersect. Hit [ENTER] 3 times, and it will calculate the point (x, y) where they intersect!

Solving Systems Algebraically PART 1: Substitution Method Section 3. 2

Solving by SUBSTITUTION •

Solving by SUBSTITUTION •

Solving by SUBSTITUTION •

STEPS 1. 2. 3. 4. 5. Solve one equation for one variable. Substitute what you get into the other equation. Solve to get the value for x or y. Substitute that value into either equation. Solve for the other variable.

Word Problems Tickets for the drama club’s production of “Hairspray” cost $8 for adults and $5 for students. On the first night of the performance, 200 tickets are sold for a total of $5375. How many of each type of ticket was sold?

STEP 1: Define the 2 variables We need to find how many of each ticket type, so let the variables be those 2 numbers! Let x = # adult tickets Let y= # student tickets
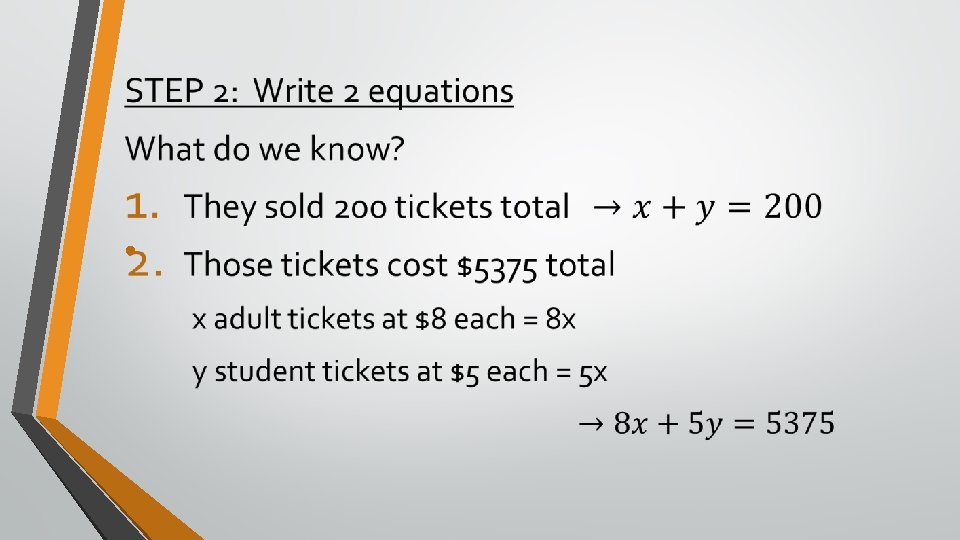


Solving Systems Algebraically PART 2: Elimination Method Section 3. 2

Solving by ELIMINATION •

Solving by ELIMINATION •

Solving by ELIMINATION •

STEPS 1. Add or subtract the 2 equations to eliminate one variable. 2. Solve for the remaining variable. 3. Substitute that value into either equation. 4. Solve for the other variable.

When Both Variables Go Away… • If you get a TRUE statement (such as 0=0) • IMS (infinitely many solutions – coinciding lines) • If you get a FALSE statement (such as 0=16) • No Solution (parallel lines)

When Adding or Subtracting will NOT Eliminate a Variable… •

When Adding or Subtracting will NOT Eliminate a Variable… •