Chapter 3 Linear Programming Sensitivity Analysis and Interpretation

Chapter 3 Linear Programming: Sensitivity Analysis and Interpretation of Solution n n Introduction to Sensitivity Analysis Graphical Sensitivity Analysis: Computer Solution Limitations of Classical Sensitivity Analysis © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 1

Introduction to Sensitivity Analysis n n In the previous chapter we discussed: • objective function value • values of the decision variables • reduced costs • slack/surplus In this chapter we will discuss: • changes in the coefficients of the objective function • changes in the right-hand side value of a constraint © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 2

Introduction to Sensitivity Analysis n n n Sensitivity analysis (or post-optimality analysis) is used to determine how the optimal solution is affected by changes, within specified ranges, in: • the objective function coefficients • the right-hand side (RHS) values Sensitivity analysis is important to a manager who must operate in a dynamic environment with imprecise estimates of the coefficients. Sensitivity analysis allows a manager to ask certain what-if questions about the problem. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 3

Graphical Sensitivity Analysis n For LP problems with two decision variables, graphical solution methods can be used to perform sensitivity analysis on • the objective function coefficients, and • the right-hand-side values for the constraints. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 4

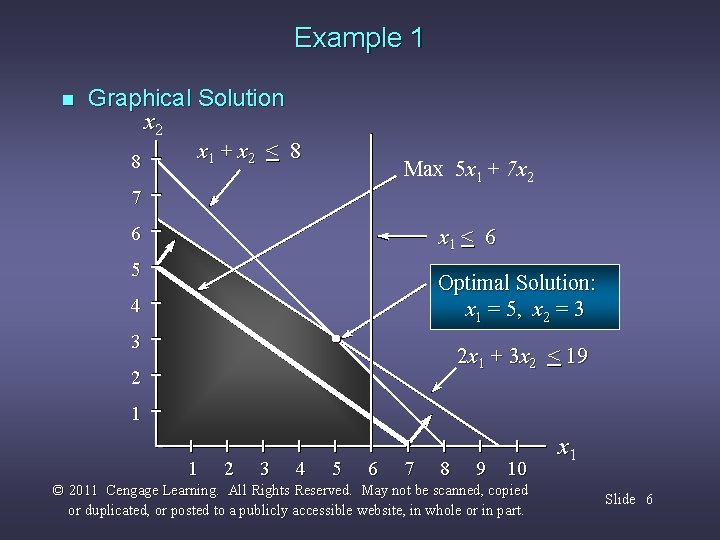
Example 1 n LP Formulation Max 5 x 1 + 7 x 2 s. t. x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1, x 2 > 0 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 5

Example 1 n Graphical Solution x 2 8 x 1 + x 2 < 8 Max 5 x 1 + 7 x 2 7 6 x 1 < 6 5 Optimal Solution: x 1 = 5, x 2 = 3 4 3 2 x 1 + 3 x 2 < 19 2 1 1 2 3 4 5 6 7 8 9 10 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. x 1 Slide 6

Objective Function Coefficients n n n Let us consider how changes in the objective function coefficients might affect the optimal solution. The range of optimality for each coefficient provides the range of values over which the current solution will remain optimal. Managers should focus on those objective coefficients that have a narrow range of optimality and coefficients near the endpoints of the range. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 7

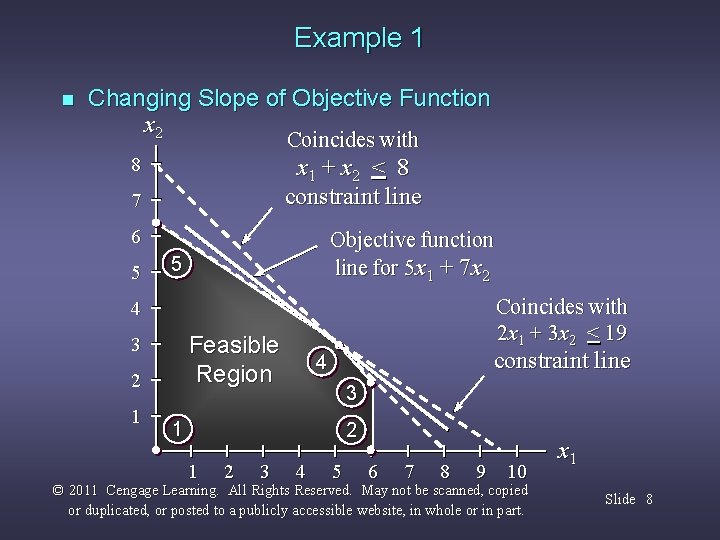
Example 1 n Changing Slope of Objective Function x 2 Coincides with 8 x 1 + x 2 < 8 constraint line 7 6 5 Objective function line for 5 x 1 + 7 x 2 5 Coincides with 2 x 1 + 3 x 2 < 19 4 Feasible Region 3 2 1 constraint line 4 3 1 2 3 4 5 6 7 8 9 10 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. x 1 Slide 8

Range of Optimality n n Graphically, the limits of a range of optimality are found by changing the slope of the objective function line within the limits of the slopes of the binding constraint lines. Slope of an objective function line, Max c 1 x 1 + c 2 x 2, is -c 1/c 2, and the slope of a constraint, a 1 x 1 + a 2 x 2 = b, is -a 1 / a 2. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 9

Example 1 n Range of Optimality for c 1 The slope of the objective function line is -c 1/c 2. The slope of the first binding constraint, x 1 + x 2 = 8, is -1 and the slope of the second binding constraint, x 1 + 3 x 2 = 19, is -2/3. Find the range of values for c 1 (with c 2 staying 7) such that the objective function line slope lies between that of the two binding constraints: -1 < -c 1/7 < -2/3 Multiplying through by -7 (and reversing the inequalities): 14/3 < c 1 < 7 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 10

Example 1 n Range of Optimality for c 1 Would a change in c 1 from 5 to 7 (with c 2 unchanged) cause a change in the optimal solution? The answer is ‘no’ because when c 1 = 7, the condition 14/3 < c 1 < 7 is satisfied. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 11

Example 1 n Range of Optimality for c 2 Find the range of values for c 2 ( with c 1 staying 5) such that the objective function line slope lies between that of the two binding constraints: -1 < -5/c 2 < -2/3 Multiplying by -1: Inverting, 1 > 5/c 2 > 2/3 1 < c 2/5 < 3/2 Multiplying by 5: 5 < c 2 < 15/2 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 12

Example 1 n Range of Optimality for c 2 Would a change in c 2 from 7 to 6 (with c 1 unchanged) cause a change in the optimal solution? The answer is ‘no’ because when c 2 = 6, the condition 5 < c 2 < 15/2 is satisfied. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 13

Simultaneous Changes n n The range of optimality for objective function coefficients is only applicable for changes made to one coefficient at a time. All other coefficients are assumed to be fixed at their initial values. If two or more coefficients are changed simultaneously, further analysis is usually necessary. However, when solving two-variable problems graphically, the analysis is fairly easy. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 14

Simultaneous Changes n n Simply compute the slope of the objective function (-Cx 1/Cx 2 ) for the new coefficient values. If this ratio is > the lower limit on the slope of the objective function and < the upper limit, then the changes made will not cause a change in the optimal solution. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 15

Example 1 n Simultaneous Changes in c 1 and c 2 Would simultaneously changing c 1 from 5 to 7 and changing c 2 from 7 to 6 cause a change in the optimal solution? (Recall that these changes individually did not cause the optimal solution to change. ) Recall that the objective function line slope must lie between that of the two binding constraints: -1 < -c 1/c 2 < -2/3 The answer is ‘yes’ the optimal solution changes because -7/6 does not satisfy the above condition. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 16

Right-Hand Sides n n Let us consider how a change in the right-hand side for a constraint might affect the feasible region and perhaps cause a change in the optimal solution. The change in the value of the optimal solution per unit increase in the right-hand side is called the dual value. The range of feasibility is the range over which the dual value is applicable. As the RHS increases, other constraints will become binding and limit the change in the value of the objective function. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 17

Dual Value n n Graphically, a dual value is determined by adding +1 to the right hand side value in question and then resolving for the optimal solution in terms of the same two binding constraints. The dual value is equal to the difference in the values of the objective functions between the new and original problems. The dual value for a nonbinding constraint is 0. A negative dual value indicates that the objective function will not improve if the RHS is increased. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 18

Example 1 n Dual Values Constraint 1: Since x 1 < 6 is not a binding constraint, its dual price is 0. Constraint 2: Change the RHS value of the second constraint to 20 and resolve for the optimal point determined by the last two constraints: 2 x 1 + 3 x 2 = 20 and x 1 + x 2 = 8. The solution is x 1 = 4, x 2 = 4, z = 48. Hence, the dual price = znew - zold = 48 - 46 = 2. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 19

Example 1 n Dual Values Constraint 3: Change the RHS value of the third constraint to 9 and resolve for the optimal point determined by the last two constraints: 2 x 1 + 3 x 2 = 19 and x 1 + x 2 = 9. The solution is: x 1 = 8, x 2 = 1, z = 47. The dual price is znew - zold = 47 - 46 = 1. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 20

Range of Feasibility n n The range of feasibility for a change in the right hand side value is the range of values for this coefficient in which the original dual value remains constant. Graphically, the range of feasibility is determined by finding the values of a right hand side coefficient such that the same two lines that determined the original optimal solution continue to determine the optimal solution for the problem. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 21

Sensitivity Analysis: Computer Solution Software packages such as Lingo and Microsoft Excel provide the following LP information: n Information about the objective function: • its optimal value • coefficient ranges (ranges of optimality) n Information about the decision variables: • their optimal values • their reduced costs n Information about the constraints: • the amount of slack or surplus • the dual prices • right-hand side ranges (ranges of feasibility) © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 22

Reduced Cost n n The reduced cost associated with a variable is equal to the dual value for the non-negativity constraint associated with the variable. In general, if a variable has a non-zero value in the optimal solution, then it will have a reduced cost equal to 0. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 23

Example 1 (Again) n LP Formulation Max 5 x 1 + 7 x 2 s. t. x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1, x 2 > 0 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 24

Example 1 n Range of Optimality for c 1 and c 2 Adjustable Cells Cell $B$8 $C$8 Final Reduced Name Value Cost X 1 5. 0 0. 0 X 2 3. 0 0. 0 Objective Coefficient 5 7 Allowable Increase 2 0. 5 Allowable Decrease 0. 3333 2 Constraints Final Cell Name Value $B$13 #1 5 $B$14 #2 19 $B$15 #3 8 Dual Value 0 2 1 Constraint Allowable R. H. Side Increase 6 1 E+30 19 5 8 0. 3333 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Allowable Decrease 1 1 1. 66666667 Slide 25

Example 1 n Dual Values Adjustable Cells Cell $B$8 $C$8 Final Reduced Name Value Cost X 1 5. 0 0. 0 X 2 3. 0 0. 0 Objective Coefficient 5 7 Allowable Increase 2 0. 5 Allowable Decrease 0. 3333 2 Constraints Final Cell Name Value $B$13 #1 5 $B$14 #2 19 $B$15 #3 8 Dual Value 0 2 1 Constraint Allowable R. H. Side Increase 6 1 E+30 19 5 8 0. 3333 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Allowable Decrease 1 1 1. 66666667 Slide 26

Example 1 n Range of Feasibility Adjustable Cells Cell $B$8 $C$8 Final Reduced Name Value Cost X 1 5. 0 0. 0 X 2 3. 0 0. 0 Objective Coefficient 5 7 Allowable Increase 2 0. 5 Allowable Decrease 0. 3333 2 Constraints Final Cell Name Value $B$13 #1 5 $B$14 #2 19 $B$15 #3 8 Dual Value 0 2 1 Constraint Allowable R. H. Side Increase 6 1 E+30 19 5 8 0. 3333 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Allowable Decrease 1 1 1. 66666667 Slide 27

Example 2: Olympic Bike Co. Olympic Bike is introducing two new lightweight bicycle frames, the Deluxe and the Professional, to be made from special aluminum and steel alloys. The anticipated unit profits are $10 for the Deluxe and $15 for the Professional. The number of pounds of each alloy needed per frame is summarized on the next slide. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 28

Example 2: Olympic Bike Co. A supplier delivers 100 pounds of the aluminum alloy and 80 pounds of the steel alloy weekly. Deluxe Professional Aluminum Alloy 2 4 Steel Alloy 3 2 How many Deluxe and Professional frames should Olympic produce each week? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 29

Example 2: Olympic Bike Co. n Model Formulation • Verbal Statement of the Objective Function Maximize total weekly profit. • Verbal Statement of the Constraints Total weekly usage of aluminum alloy < 100 pounds. Total weekly usage of steel alloy < 80 pounds. • Definition of the Decision Variables x 1 = number of Deluxe frames produced weekly. x 2 = number of Professional frames produced weekly. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 30

Example 2: Olympic Bike Co. n Model Formulation (continued) Max 10 x 1 + 15 x 2 s. t. (Total Weekly Profit) 2 x 1 + 4 x 2 < 100 (Aluminum Available) 3 x 1 + 2 x 2 < 80 (Steel Available) x 1, x 2 > 0 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 31

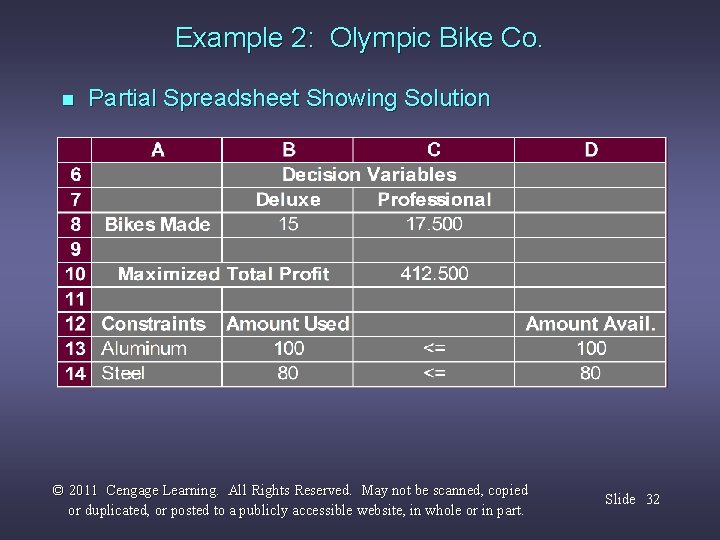
Example 2: Olympic Bike Co. n Partial Spreadsheet Showing Solution © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 32

Example 2: Olympic Bike Co. n Optimal Solution According to the output: x 1 (Deluxe frames) = 15 x 2 (Professional frames) = 17. 5 Objective function value = $412. 50 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 33

Example 2: Olympic Bike Co. n Range of Optimality Question: Suppose the profit on deluxe frames is increased to $20. Is the above solution still optimal? What is the value of the objective function when this unit profit is increased to $20? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 34

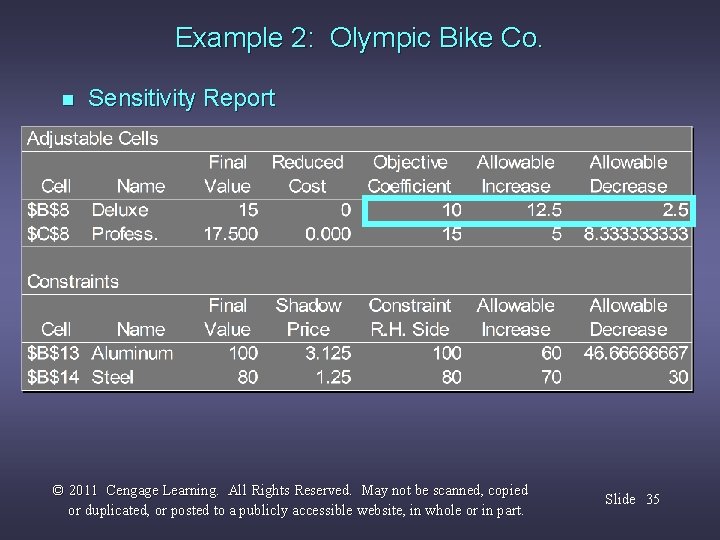
Example 2: Olympic Bike Co. n Sensitivity Report © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 35

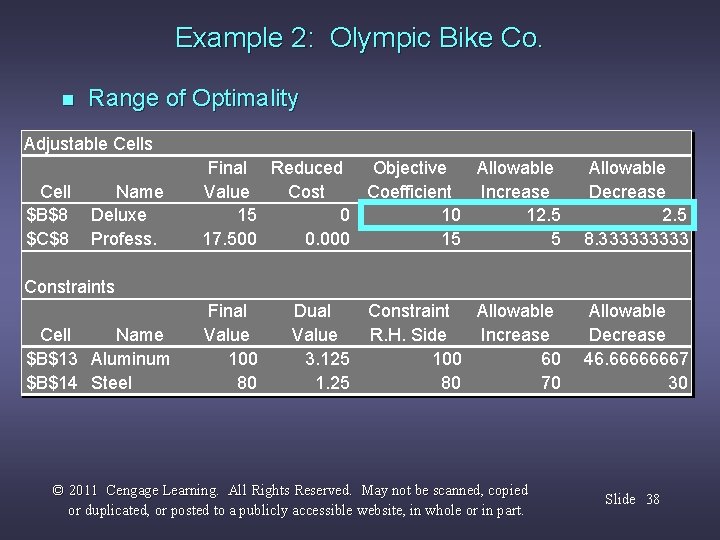
Example 2: Olympic Bike Co. n Range of Optimality Answer: The output states that the solution remains optimal as long as the objective function coefficient of x 1 is between 7. 5 and 22. 5. Because 20 is within this range, the optimal solution will not change. The optimal profit will change: 20 x 1 + 15 x 2 = 20(15) + 15(17. 5) = $562. 50. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 36

Example 2: Olympic Bike Co. n Range of Optimality Question: If the unit profit on deluxe frames were $6 instead of $10, would the optimal solution change? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 37

Example 2: Olympic Bike Co. n Range of Optimality Adjustable Cells Cell $B$8 $C$8 Name Deluxe Profess. Final Reduced Objective Allowable Value Cost Coefficient Increase 15 0 10 12. 5 17. 500 0. 000 15 5 Allowable Decrease 2. 5 8. 33333 Final Value 100 80 Allowable Decrease 46. 66666667 30 Constraints Cell Name $B$13 Aluminum $B$14 Steel Dual Value 3. 125 1. 25 Constraint Allowable R. H. Side Increase 100 60 80 70 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 38

Example 2: Olympic Bike Co. n Range of Optimality Answer: The output states that the solution remains optimal as long as the objective function coefficient of x 1 is between 7. 5 and 22. 5. Because 6 is outside this range, the optimal solution would change. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 39

Limitations of Classical Sensitivity Analysis n n n Classical sensitivity analysis provided by most computer packages does have its limitations. It is rarely the case that one solves a model once and makes recommendations. More often, a series of models is solved using a variety of input data sets before a final plan is adopted. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 40

Limitations of Classical Sensitivity Analysis n Simultaneous Changes The range analysis for objective function coefficients and the constraint right-hand sides is only applicable for changes in a single coefficient. We should resolve the model with the new coefficient values. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 41

Limitations of Classical Sensitivity Analysis n Changes in Constraint Coefficients Classical sensitivity analysis provides no information about changes resulting from a change in a coefficient of a variable in a constraint. We must simply change the coefficient and rerun the model. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 42

Limitations of Classical Sensitivity Analysis n Non-intuitive Dual Values Constraints with variables naturally on both the lefthand right-hand sides often lead to dual values that have a non-intuitive explanation. This is often the case with constraints that involve percentages. The model should be resolved with the new percentages. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 43

Example 3 n Consider the following linear program: Min 6 x 1 + 9 x 2 s. t. ($ cost) x 1 + 2 x 2 < 8 10 x 1 + 7. 5 x 2 > 30 x 2 > 2 x 1, x 2 > 0 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 44

Example 3 n Computer Output OBJECTIVE FUNCTION VALUE = 27. 000 Variable x 1 x 2 Constraint 1 2 3 Value 1. 500 2. 000 Slack/Surplus 2. 500 0. 000 Reduced Cost 0. 000 Dual Value 0. 000 -0. 600 -4. 500 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 45

Example 3 n Computer Output (continued) OBJECTIVE COEFFICIENT RANGES Variable Lower Limit Current Value x 1 0. 000 6. 000 12. 000 x 2 4. 500 9. 000 Limit Upper Limit No RIGHTHAND SIDE RANGES Constraint Lower Limit Current Value Upper Limit 1 5. 500 8. 000 No Limit 2 15. 000 30. 000 55. 000 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied Slide 46 or duplicated, or posted to a publicly accessible website, in whole or in part. 3 0. 000 2. 000

Example 3 n Optimal Solution According to the output: x 1 = 1. 5 x 2 = 2. 0 Objective function value = 27. 00 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 47

Example 3 n Range of Optimality Question: Suppose the unit cost of x 1 is decreased to $4. Is the current solution still optimal? What is the value of the objective function when this unit cost is decreased to $4? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 48

Example 3 n Computer Output OBJECTIVE COEFFICIENT RANGES Variable Lower Limit Current Value x 1 0. 000 6. 000 12. 000 x 2 4. 500 9. 000 Limit Upper Limit No RIGHTHAND SIDE RANGES Constraint Lower Limit Current Value Upper Limit 1 5. 500 8. 000 No Limit © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied Slide 49 2 15. 000 30. 000 or duplicated, or posted to a publicly accessible website, in whole or in part. 55. 000

Example 3 n Range of Optimality Answer: The output states that the solution remains optimal as long as the objective function coefficient of x 1 is between 0 and 12. Because 4 is within this range, the optimal solution will not change. However, the optimal total cost will be affected: 6 x 1 + 9 x 2 = 4(1. 5) + 9(2. 0) = $24. 00. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 50

Example 3 n Range of Optimality Question: How much can the unit cost of x 2 be decreased without concern for the optimal solution changing? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 51

Example 3 n Computer Output OBJECTIVE COEFFICIENT RANGES Variable Lower Limit Current Value x 1 0. 000 6. 000 12. 000 x 2 4. 500 9. 000 Limit Upper Limit No RIGHTHAND SIDE RANGES Constraint Lower Limit Current Value Upper Limit 1 5. 500 8. 000 No Limit © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied Slide 52 2 15. 000 30. 000 or duplicated, or posted to a publicly accessible website, in whole or in part. 55. 000

Example 3 n Range of Optimality Answer: The output states that the solution remains optimal as long as the objective function coefficient of x 2 does not fall below 4. 5. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 53

Example 3 n Range of Feasibility Question: If the right-hand side of constraint 3 is increased by 1, what will be the effect on the optimal solution? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 54

Example 3 n Computer Output OBJECTIVE COEFFICIENT RANGES Variable Lower Limit Current Value x 1 0. 000 6. 000 12. 000 x 2 4. 500 9. 000 Limit Upper Limit No RIGHTHAND SIDE RANGES Constraint Lower Limit Current Value Upper Limit 1 5. 500 8. 000 No Limit © 2011 Cengage Reserved. May not be scanned, copied 2 Learning. All Rights 15. 000 30. 000 Slide 55 or duplicated, or posted to a publicly accessible website, in whole or in part. 55. 000

Example 3 n Range of Feasibility Answer: A dual value represents the improvement in the objective function value per unit increase in the righthand side. A negative dual value indicates a deterioration (negative improvement) in the objective, which in this problem means an increase in total cost because we're minimizing. Since the right-hand side remains within the range of feasibility, there is no change in the optimal solution. However, the objective function value increases by $4. 50. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 56