Chapter 3 Lexical Analysis 1 Interaction of lexical

Chapter 3. Lexical Analysis (1)

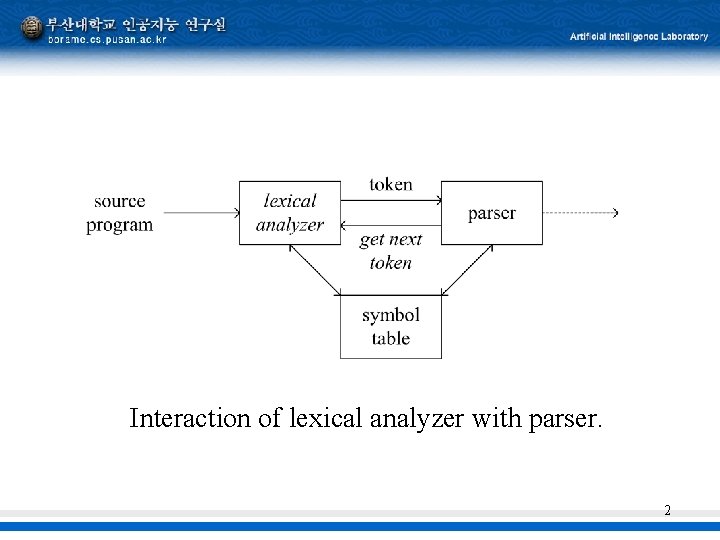
Interaction of lexical analyzer with parser. 2

Lexical Analysis § Issues – Simpler design is preferred – Compiler efficiency is improved – Compiler portability is improved § Terms – Tokens terminal symbols in a grammar – Patterns rules to describing strings of a token – Lexemes a set of strings matched by the pattern 3

TOKEN SAMPLE LEXEMES INFORMAL DESCRIPTION OF PATTERN const if if if relation <, <=, =, <>, >, >= < or <= or < > or >= or > id pi, count, D 2 letter followed by letters and digits num 3. 1416, 0, 6. 02 E 23 any numeric constant literal "core dumped" any characters between " and " except " Examples of tokens. 4

Difficulties in implementing lexical analyzers § FORTRAN – No delimiter is used – DO 5 I=1. 25 DO 5 I=1, 25 DO 5 I= 1 25 § PL/I – Keywords are not reserved – IF THEN = ELSE; ELSE=THEN; 5

Attributes for tokens § A lexical analyzer collects information about tokens into their associated attributes § Example – E = M * C ** 2 • • <id, pointer to symbol-table entry for E> <assign_op, > <id, pointer to symbol-table entry for M> <mult_op, _> <id, pointer to symbol-table entry for C> <exp_op, > <num, integer value 2> generally stored in constant table 6

Lexical Errors § Rules for error recovery – – Deleting an extraneous character Inserting a missing character Replacing an incorrect character by a correct character Transposing two adjacent characters § Minimum-distance erroneous correction § Example – Detectable : 2 as 3, 2#31, … – Undetectable : fi(a == f(x)) … 7

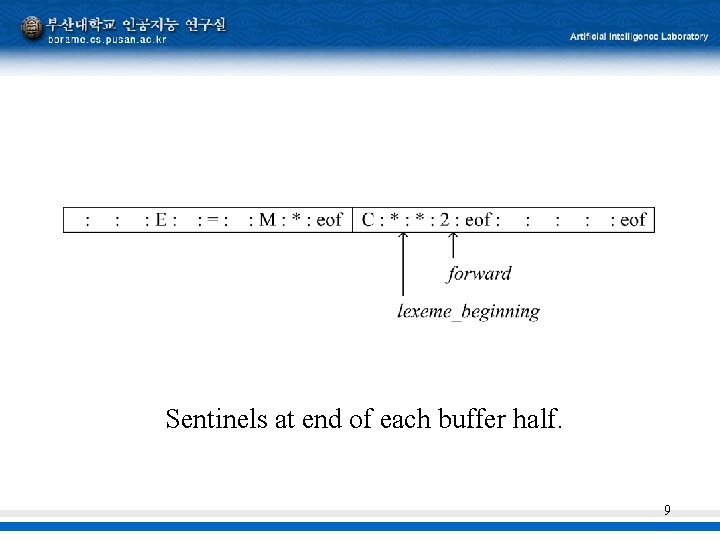
Input Buffering § A single buffer could make a big difficulty – 두 버퍼 사이에 있는 word – Declare (arg 1, …. , argn) array or function § Buffer pairs – A good solution – Sentinels을 쓰면 매번 버퍼의 끝인지와 파일 의 끝인지를 동시에 검사할 필요가 없음 8

Sentinels at end of each buffer half. 9

Specification of Tokens § Strings and languages – – – Alphabet or character class finite set of symbols String sentence word |s| length of a string s ε : empty string, Ф ={ε} : empty set x, y are strings • xy : concatenation, εx = x ε = x § Operations on languages 10

TERM DEFINTION prefix of s A string obtained by removing zero or more trailing symbols of string s; e. g. , ban is a prefix of banana. suffix of s A string formed by deleting zero or more of the leading symbols of s; e. g. , nana is a suffix of banana. substring of s A string obtained by deleting a prefix and a suffix from s; e. g. , nan is a substring of banana. Every prefix and every suffix of s is a substring of s, but not every substring of s is a prefix or a suffix of s. For every string s, both s and are prefixes, suffixes, and substrings of s. proper prefix, suffix, or substring of s Any nonempty string x that is, respectively, a prefix, suffix, or substring of s such that s x. subsequence of s Any string formed by deleting zero or more not necessarily contiguous symbols from s; e. g. , baaa is a subsequence of banana. Terms for parts of a string. 11

OPERATION DEFINITION union of L and M written L M = {s | s is in L or s is in M} concatenation of L and M written LM LM = { st | s is in L and t is in M } Kleene closure of L written L* positive closure of L written L+ L* denotes “zero or more concatenations of” L. L+ denotes “one or more concatenations of” L. Definitions of operations on languages. 12

Regular Expressions 1. is a regular expression that denotes { }, that is, the set containing the empty string. 2. If a is symbol in , then a is a regular expression that denotes {a}, i. e. , the set containing the string a. Although we use the same notation for all three, technically, the regular expression a is different from the string a or the symbol a. It will be clear from the context whether we are talking about a as a regular expression, string, or symbol. 3. Suppose r and s are regular expressions denoting the language L(r) and L(s). Then, a) b) c) d) (r)|(s) is a regular expression denoting L(r) L(s). (r)(s) is a regular expression denoting L(r)L(s). (r)* is a regular expression denoting (L(r))*. (r) is a regular expression denoting L(r). 13

Examples on operations in regular expressions § Σ ={a, b} alphabets – a | b {a, b} – (a|b)(c|d) {ac, ad, bc, bd} – a* {ε, a, aaa, …} – (a|b)* (a*|b*)* – aa* = a+, ε|a+ = a* – (a|b) = (b|a) 14

AXIOM r|s = s|r r|(s|t) = (r|s)|t DESCRIPTION | is commutative | is associative (rs)t = r(st) concatenation is associative r(s|t) = rs|rt (s|t)r = sr|tr concatenation distributes over | r = r r* = (r| )* r** = r* is the identity element for concatenation relation between * and * is idempotent Algebraic properties of regular expressions. 15

Regular Definitions § Regular definition – d 1 r 1 d 2 r 2 …. dn rn • 예 • letter A|B| … |Z|a|b| … |z • digit 0|1| … | 9 • id letter (letter|digit)* 16

Unsigned numbers § Pascal digit 0|1| … |9 digits digit* operational_fraction . digits | ε optional_exponent (E(+|-| ε) digits | ε num digits operational_fraction optional_exponent 17

Notational Shorthands (1/2) 1. One or more instances. The unary postfix operator + means “one or more instances of. ” If r is a regular expression that denotes the language L(r), then (r)+ is a regular expression that denotes the language (L(r))+. Thus, the regular expression a+ denotes the set of all strings of one or more a’s. The operator + has the same precedence and associativity as the operator *. The two algebraic identities r* = r+| and r+ = rr* relate the Kleene and positive closure operators. 2. Zero or one instance. The unary postfix operator ? means “zero or one instance of. ” The notation r? is a shorthand for r|. If r is a regular expression, then, (r)? is a regular expression that denotes the language L(r) { }. For example, using the + and ? operators, we can rewrite the regular definition for num in Example 3. 5 as 18

Notational Shorthands (2/2) digits optional _fraction optional_exponent num 3. 0 | 1 | ··· | 9 digit+ (. digits )? ( E ( + | - )? digits )? Digits optional_fraction optional_exponent Character classes. The notation [abc] where a, b, and c are alphabet symbols denotes the regular expression a | b | c. An abbreviated character class such as [a – z] denotes the regular expression a | b | ··· | z. Using character classes, we can describe identifiers as being strings generated by the regular expression [A – Za – z][A – Za – z 0 – 9]* 19

Nonregular set § {wcw-1|w is a string of a’s and b’s} context-free grammar is required to represent the string 20

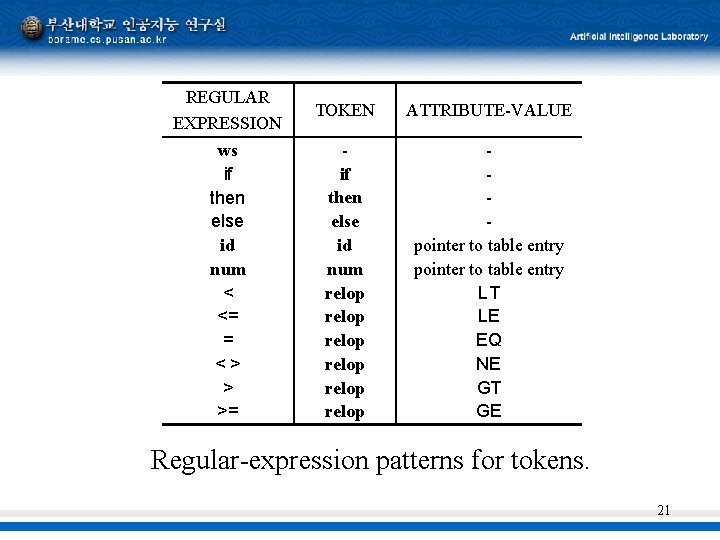
REGULAR EXPRESSION TOKEN ATTRIBUTE-VALUE ws if then else id num < <= = <> > >= if then else id num relop relop pointer to table entry LT LE EQ NE GT GE Regular-expression patterns for tokens. 21

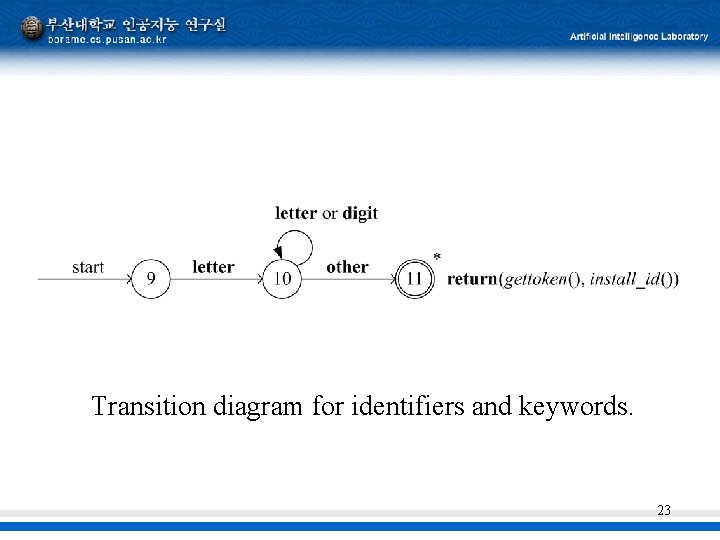
Transition diagram § § § Finite-state automata states and edges 몇 가지 예를 보여줌 …. 다음 페이지, 그림 3. 14는 앞의 예를 바탕으로 그림 22

Transition diagram for identifiers and keywords. 23

Lex에 의한 구현 § Regular definition finite automata, transition diagram § C프로그램으로 출력 § Lexical analysis, pattern matching, … 24

Creating a lexical analyzer with Lex. 25

%{ /*definitions of manifest constants LT, LE, EQ, NE, GT, GE, IF, THEN, ELSE, ID, NUMBER, RELOP */ %} /*regular definitions */ delim [ tn] ws { delim }+ letter [ A-Za-z ] digit [0– 9] id { letter } ( { letter } | { digit } )* number { digit } + ( . { digit } + ) ? ( E [ + - ] ? { digit } + ) ? Lex program for the tokens of Fig. 3. 10. (1/2) 26

%% { ws } if then else { id } { number } “<” “<=” “<>” “>=” %% { /* no action and no return */ } { return(IF); } { return(THEN); } { return(ELSE); } { yylval = install_id(); return(ID); } { yylval = install_num(); return(NUMBER); } { yylval = LT; return(RELOP); } { yylval = LE; return(RELOP); } { yylval = EQ; return(RELOP); } { yylval = NE; return(RELOP); } { yylval = GT; return(RELOP); } { yylval = GE; return(RELOP); } install_id() { /* procedure to install the lexeme, whose first character is pointed to by yytext and whose length is yyleng, into the symbol table and return a pointer thereto */ } install_num() { /* similar procedure to install a lexeme that is a number */ } Lex program for the tokens of Fig. 3. 10. (2/2) 27

Lookahead operator § DO 5 I = 1. 25 DO 5 I=1, 25 – DO/({letter | digit})* = ({letter} | {digit})*, – DO/{id}* = {digit}*, § IF(I, J)=3 IF(condition) statement – IF/ (. * ) {letter} 28