Chapter 3 Lesson 4 Objective To classify polygons

Chapter 3 Lesson 4 Objective: To classify polygons.
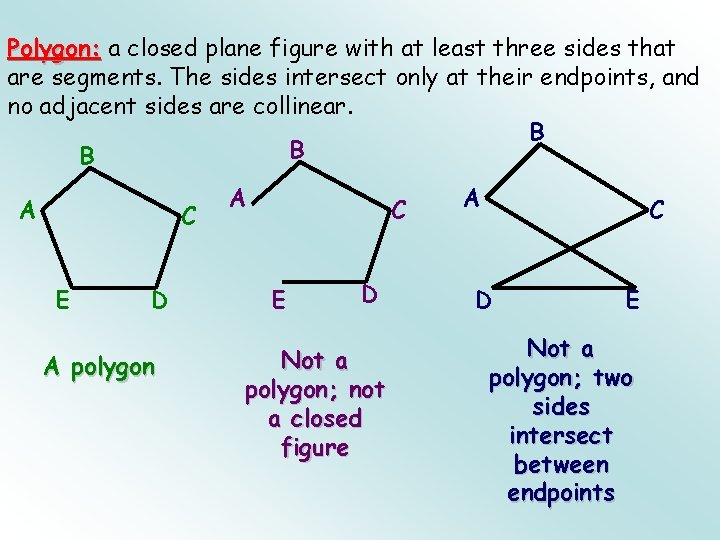
Polygon: a closed plane figure with at least three sides that are segments. The sides intersect only at their endpoints, and no adjacent sides are collinear. B B B A C E D A polygon A C E D Not a polygon; not a closed figure A C D E Not a polygon; two sides intersect between endpoints

Example 1: Naming a Polygon Name the polygon. Then identify its vertices, vertices sides, sides and angles B To name a polygon, start at any vertex and list the vertices consecutively in a clockwise or counterclockwise direction. Two names for this polygon are ABCDE and CDEAB. Vertices: A, B, C, D, E Sides: AB, BC, CD, DE, EA Angles: A, B, C, D, E A C E D
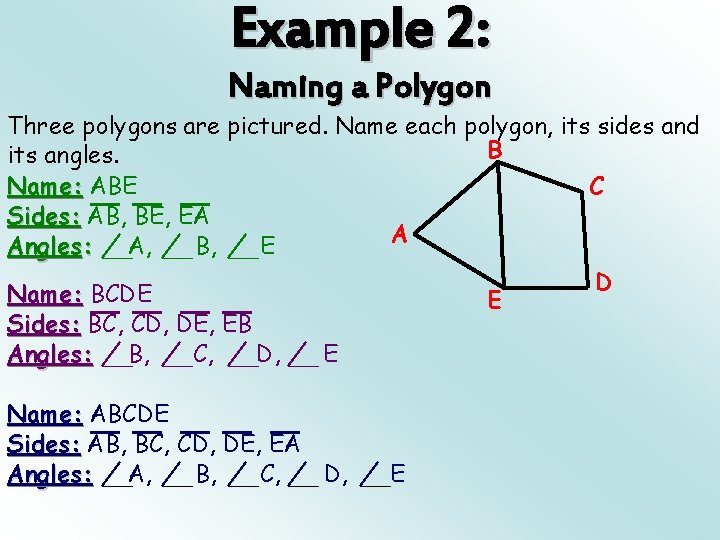
Example 2: Naming a Polygon Three polygons are pictured. Name each polygon, its sides and B its angles. Name: ABE C Sides: AB, BE, EA A Angles: A, B, E Name: BCDE Sides: BC, CD, DE, EB Angles: B, C, D, E E Name: ABCDE Sides: AB, BC, CD, DE, EA Angles: A, B, C, D, E D
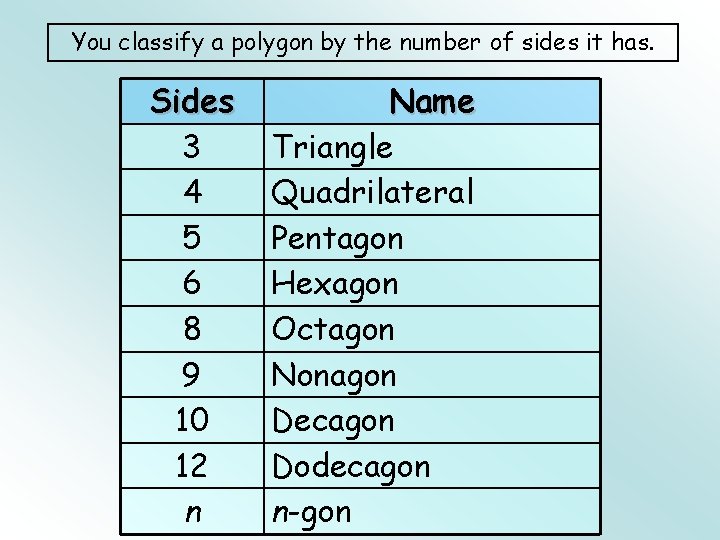
You classify a polygon by the number of sides it has. Sides 3 4 5 6 8 9 10 12 n Name Triangle Quadrilateral Pentagon Hexagon Octagon Nonagon Decagon Dodecagon n-gon
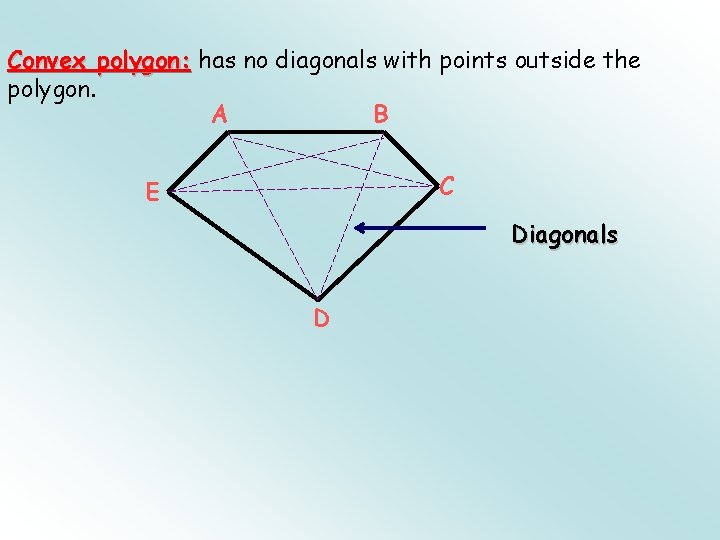
Convex polygon: has no diagonals with points outside the polygon. A B C E Diagonals D
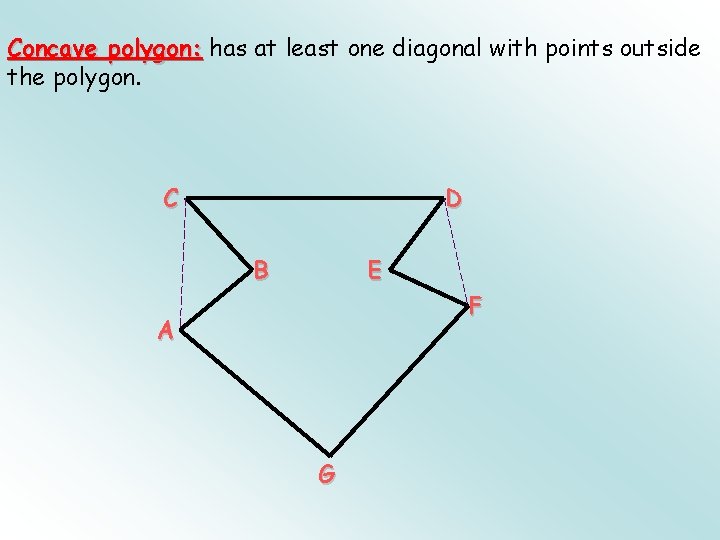
Concave polygon: has at least one diagonal with points outside the polygon. C D B E F A G
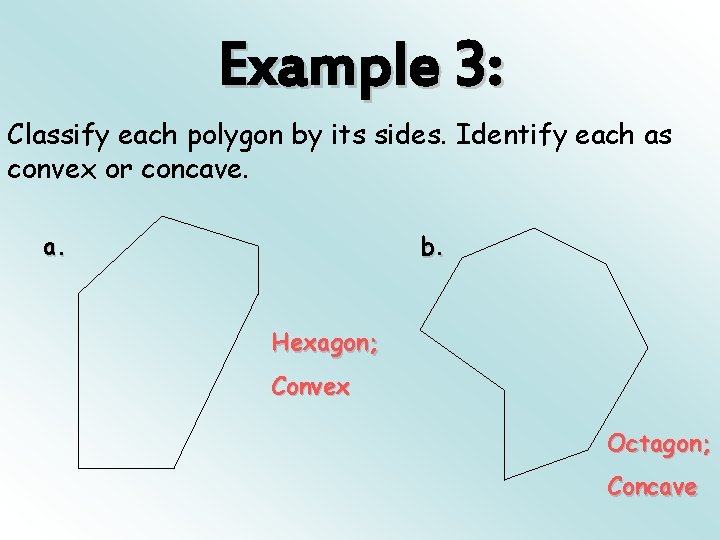
Example 3: Classify each polygon by its sides. Identify each as convex or concave. a. b. Hexagon; Convex Octagon; Concave

Theorem 3 -9: Polygon Angle-Sum Theorem The sum of the measures of the angles of n-gon is (n-2)180 Example 4: Find the sum of the measures of the angles of a 15 -gon. For a 15 -gon, n = 15 Sum = (n – 2)180 (15 – 2)180 13 • 180 2340 Polygon Angle-Sum Theorem Substitute Simplify

Example 5: Finding a Polygon Angle Sum Find the sum of the measures of the angles of a decagon. Decagon = 10 (n-2)180 (10 -2)180 8 • 180 1440
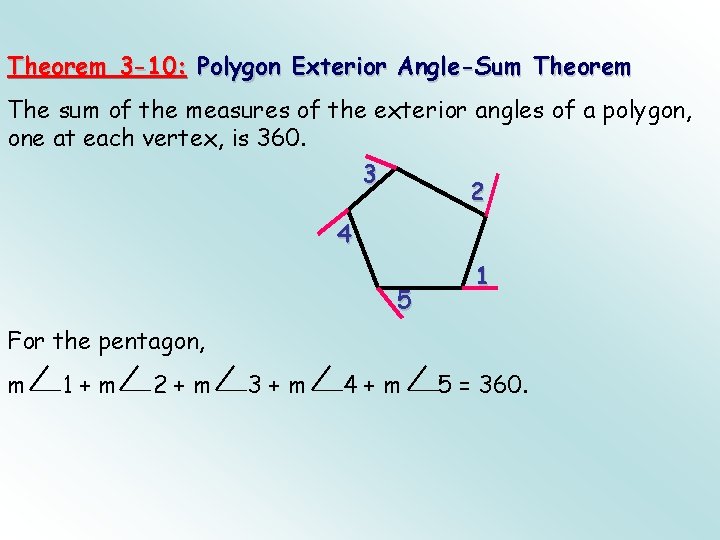
Theorem 3 -10: Polygon Exterior Angle-Sum Theorem The sum of the measures of the exterior angles of a polygon, one at each vertex, is 360. 3 2 4 5 1 For the pentagon, m 1+m 2+m 3+m 4+m 5 = 360.
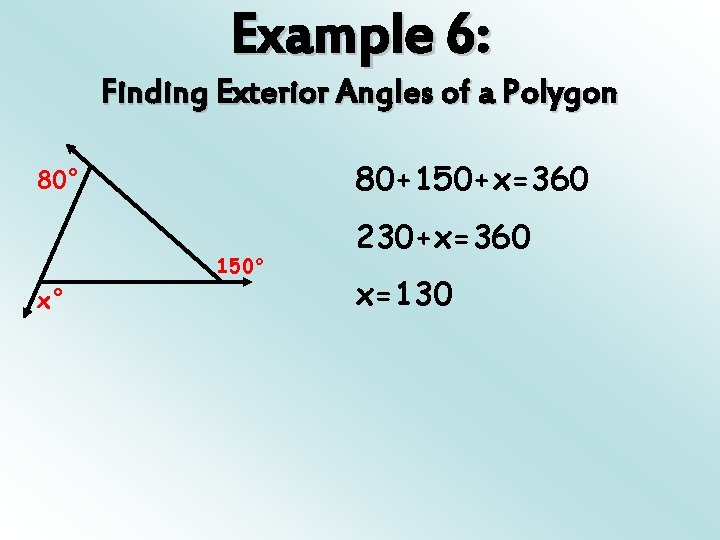
Example 6: Finding Exterior Angles of a Polygon 80+150+x=360 80° 150° x° 230+x=360 x=130
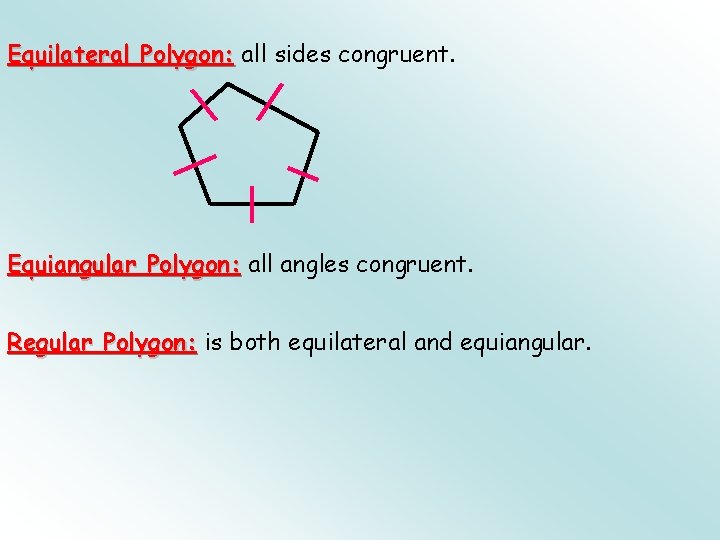
Equilateral Polygon: all sides congruent. Equiangular Polygon: all angles congruent. Regular Polygon: is both equilateral and equiangular.

Homework Page 147 – 149 #1 -25; 32 – 35; 47 - 49
- Slides: 14