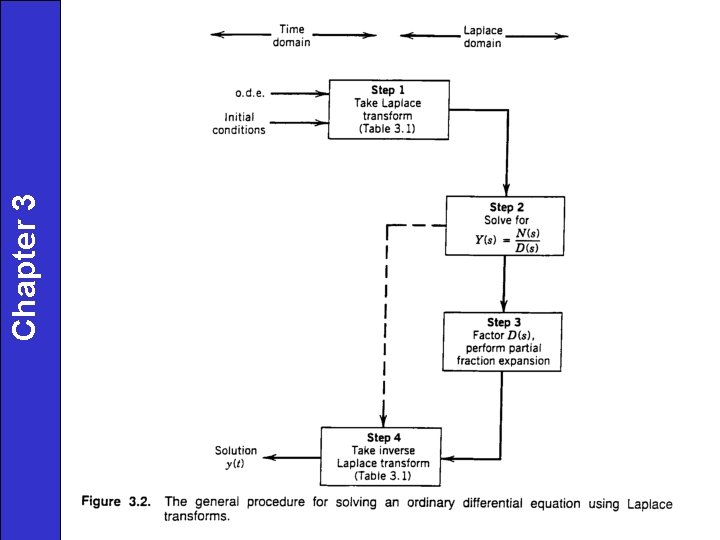
Chapter 3 Laplace Transforms 1 Standard notation in

Chapter 3 Laplace Transforms 1. Standard notation in dynamics and control (shorthand notation) 2. Converts mathematics to algebraic operations 3. Advantageous for block diagram analysis

Laplace Transform Chapter 3 Example 1: Usually define f(0) = 0 (e. g. , the error)

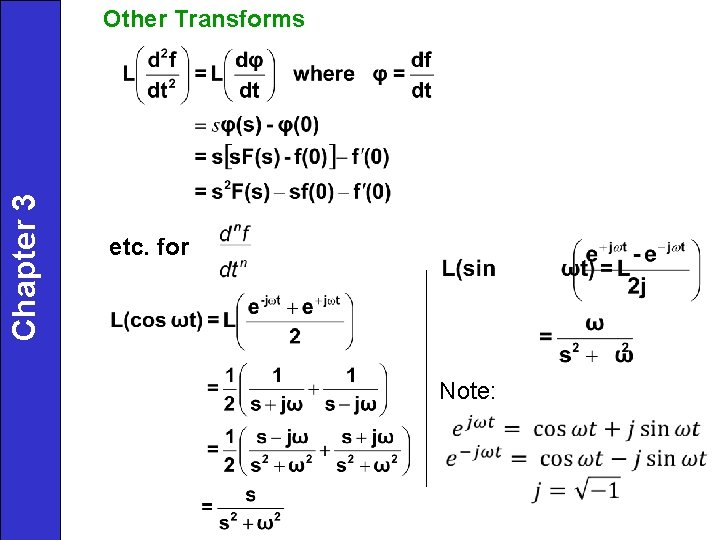
Chapter 3 Other Transforms etc. for Note:

Chapter 3

Table 3. 1 Laplace Transforms for Various Time-Domain Functionsa Chapter 3 f(t) F(s)

Table 3. 1 Laplace Transforms for Various Time-Domain Functionsa Chapter 3 f(t) F(s)

Table 3. 1 Laplace Transforms for Various Time-Domain Functionsa (continued) f(t) F (s)

Example 3. 1 Chapter 3 Solve the ODE, First, take L of both sides of (3 -26), Rearrange, Take L-1, From Table 3. 1 (line 11),

Chapter 3 Example: system at rest (s. s. ) Step 1 Take L. T. (note zero initial conditions)

Rearranging, Chapter 3 Step 2 a. Factor denominator of Y(s) Step 2 b. Use partial fraction decomposition Multiply by s, set s = 0

Chapter 3 For a 2, multiply by (s+1), set s=-1 (same procedure for a 3, a 4) Step 3. Take inverse of L. T. (check original ODE) You can use this method on any order of ODE, limited only by factoring of denominator polynomial (characteristic equation) Must use modified procedure for repeated roots, imaginary roots

Laplace transforms can be used in process control for: Chapter 3 1. Solution of differential equations (linear) 2. Analysis of linear control systems (frequency response) 3. Prediction of transient response for different inputs

Factoring the denominator polynomial Chapter 3 1. Transforms to e-t/3, e-t Real roots = no oscillation

Chapter 3 2. Transforms to Complex roots = oscillation From Table 3. 1, line 17 and 18

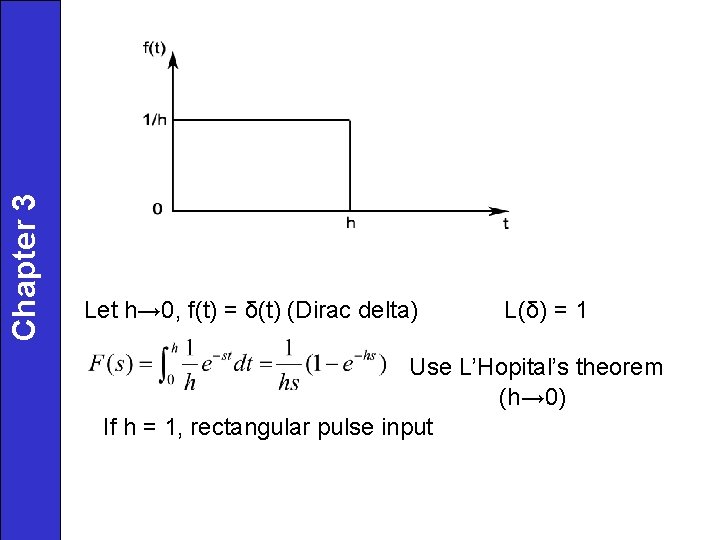
Chapter 3 Let h→ 0, f(t) = δ(t) (Dirac delta) L(δ) = 1 Use L’Hopital’s theorem (h→ 0) If h = 1, rectangular pulse input

Difference of two step inputs S(t) – S(t-1) (S(t-1) is step starting at t = h = 1) Chapter 3 By Laplace transform Can be generalized to steps of different magnitudes (a 1, a 2).

Chapter 3 One other useful feature of the Laplace transform is that one can analyze the denominator of the transform to determine its dynamic behavior. For example, if the denominator can be factored into (s+2)(s+1). Using the partial fraction technique The step response of the process will have exponential terms e-2 t and e-t, which indicates y(t) approaches zero. However, if We know that the system is unstable and has a transient response involving e 2 t and e-t. e 2 t is unbounded for large time. We shall use this concept later in the analysis of feedback system stability.

Other applications of L( ): A. Final value theorem Chapter 3 “offset” Example 3: step response offset (steady state error) is a. B. Time-shift theorem y(t)=0 t < θ

Chapter 3 C. Initial value theorem by initial value theorem by final value theorem

Chapter 3 Previous chapter Next chapter