Chapter 3 Kinematics in Two Dimensions Vectors Learning

Chapter 3 Kinematics in Two Dimensions; Vectors

Learning objectives At the end of the chapter, students will be able to; • 1. Apply the definitions of scalar and vector to categorize different physical quantities. • 2. Use the geometric interpretation of vector addition, subtraction and multiplication to find the resultant vectors of those operations. • 3. Represent vectors in terms of magnitude and directions. • 4. Represent vectors in terms of x and y components.

Learning objectives • 5. Perform arithmetic operations with vectors using their components. • 6. Describe projectile motion in two dimensions. • 7. Apply the two-dimensional kinematics equations to motion with constant acceleration near the surface of the earth.

Units of Chapter 3 Ø Vectors and their properties Ø Addition of Vectors – Graphical Methods Ø Subtraction of Vectors, and Multiplication of a Vector by a Scalar Ø Adding Vectors by Components Ø Projectile Motion Ø Solving Problems Involving Projectile Motion

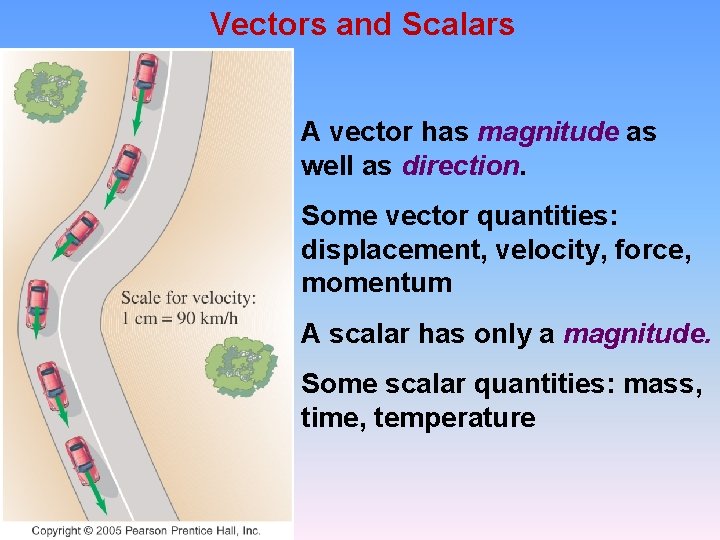
Vectors and Scalars A vector has magnitude as well as direction. Some vector quantities: displacement, velocity, force, momentum A scalar has only a magnitude. Some scalar quantities: mass, time, temperature

Vector Notation • When handwritten, use an arrow: • When printed, will be in bold print with an arrow: • When dealing with just the magnitude of a vector in print, an italic letter will be used: A – Italics will also be used to represent scalars

Properties of Vectors • Equality of Two Vectors – Two vectors are equal if they have the same magnitude and the same direction • Movement of vectors in a diagram – Any vector can be moved parallel to itself without being affected

Adding Vectors • When adding vectors, their directions must be taken into account • Units must be the same • Geometric Methods – Use scale drawings • Algebraic Methods • The resultant vector (sum) is denoted as

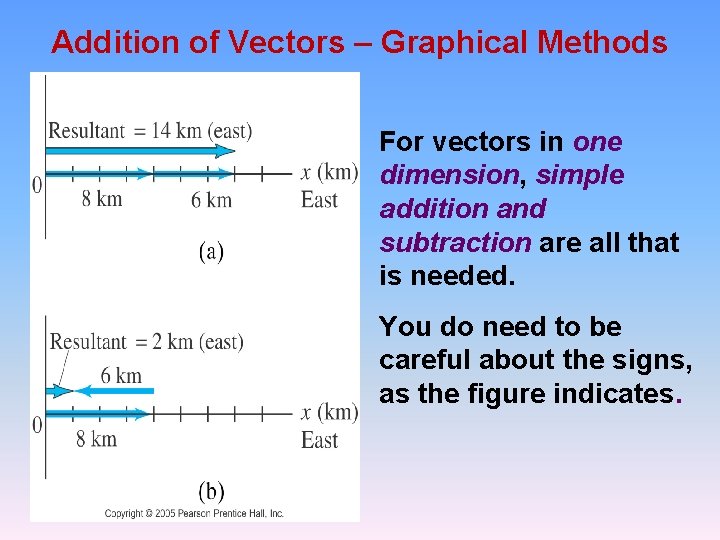
Addition of Vectors – Graphical Methods For vectors in one dimension, simple addition and subtraction are all that is needed. You do need to be careful about the signs, as the figure indicates.

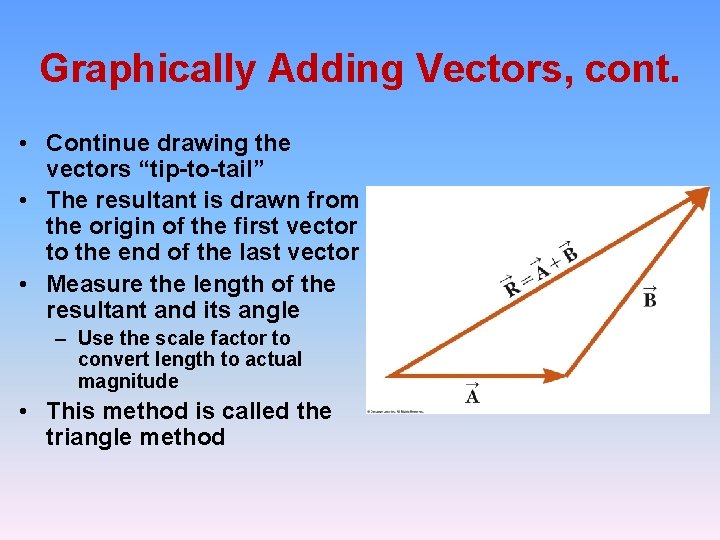
Graphically Adding Vectors, cont. • Continue drawing the vectors “tip-to-tail” • The resultant is drawn from the origin of the first vector to the end of the last vector • Measure the length of the resultant and its angle – Use the scale factor to convert length to actual magnitude • This method is called the triangle method

Notes about Vector Addition • Vectors obey the Commutative Law of Addition – The order in which the vectors are added doesn’t affect the result –

Graphically Adding Vectors, cont. • When you have many vectors, just keep repeating the “tip-totail” process until all are included • The resultant is still drawn from the origin of the first vector to the end of the last vector

More Properties of Vectors • Negative Vectors – The negative of the vector is defined as the vector that gives zero when added to the original vector – Two vectors are negative if they have the same magnitude but are 180° apart (opposite directions) –

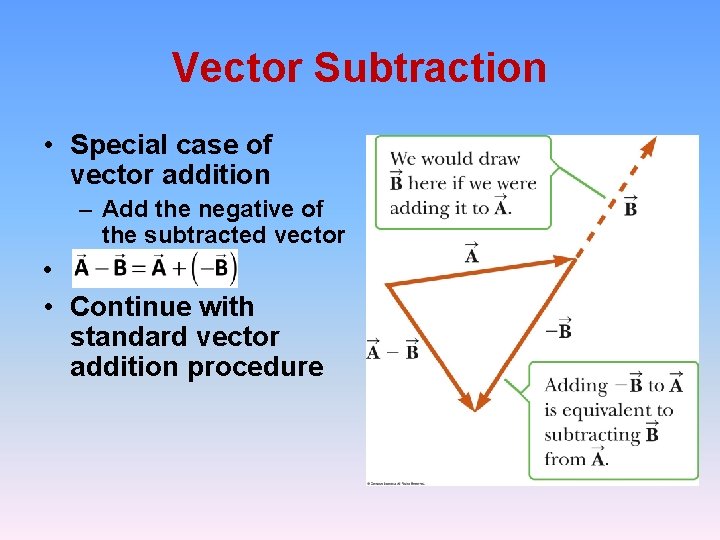
Vector Subtraction • Special case of vector addition – Add the negative of the subtracted vector • • Continue with standard vector addition procedure

Multiplying or Dividing a Vector by a Scalar • The result of the multiplication or division is a vector • The magnitude of the vector is multiplied or divided by the scalar • If the scalar is positive, the direction of the result is the same as of the original vector • If the scalar is negative, the direction of the result is opposite that of the original vector

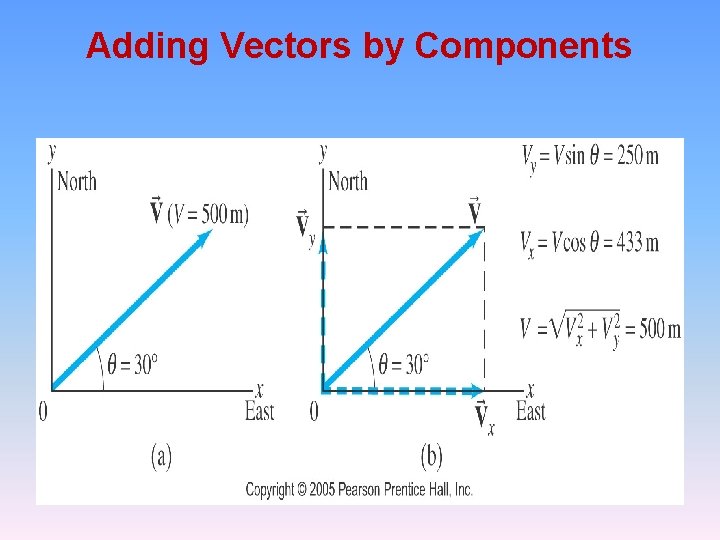
Adding Vectors by Components Any vector can be expressed as the sum of two other vectors, which are called its components. Usually the other vectors are chosen so that they are perpendicular to each other. The process of finding components is – resolving the vector into its component

Adding Vectors by Components If the components are perpendicular, they can be found using trigonometric functions.

Adding Vectors by Components

Adding Vectors by Components The components are effectively one-dimensional, so they can be added arithmetically: The components of V = V 1 + V 2 are Vx = V 1 x + V 2 x and Vy = V 1 y + V 2 y

Adding Vectors by Components Adding vectors: 1. Draw a diagram; add the vectors graphically. 2. Choose x and y axes. 3. Resolve each vector into x and y components. 4. Calculate each component using sines and cosines. 5. Add the components in each direction. 6. To find the length and direction of the vector, use:

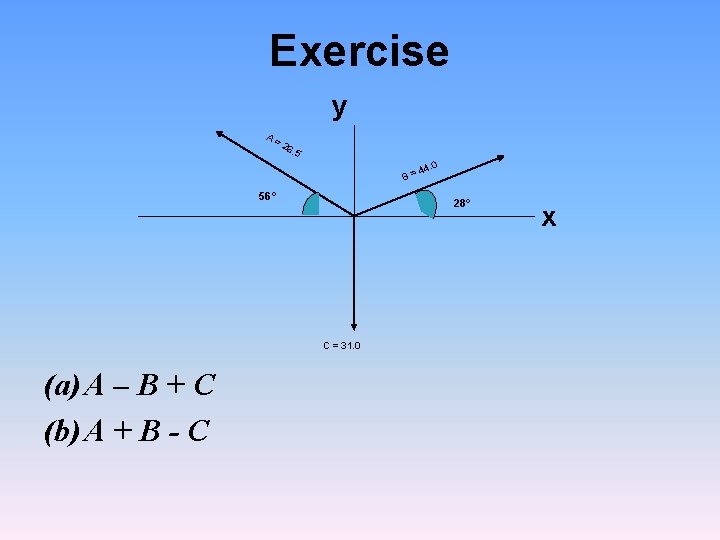
Exercise Find the x and y components of 25 m displacement at an angle of 210° relative to positive x- axis.

Exercise y A= 26 . 5 B= 56° 28° C = 31. 0 (a) A – B + C (b) A + B - C 44. 0 x

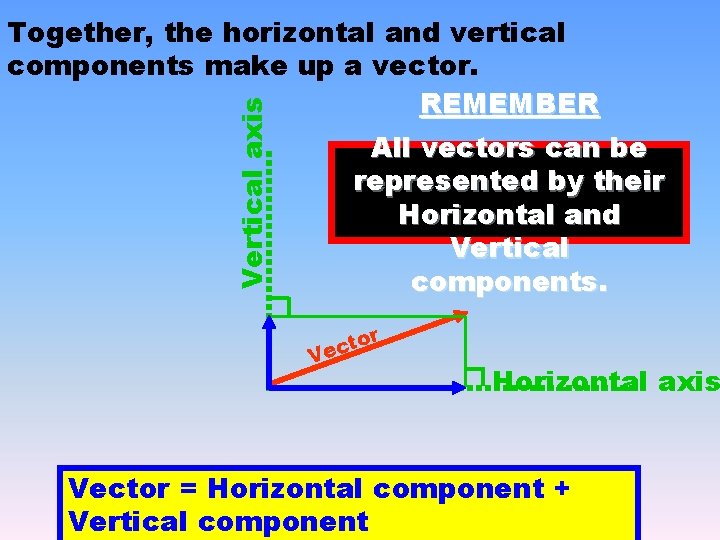
Vertical axis Together, the horizontal and vertical components make up a vector. REMEMBER All vectors can be represented by their Horizontal and Vertical components. or t c Ve Horizontal axis Vector = Horizontal component + Vertical component

m e R r e b em “North” is “Up” “South” is “Down” “East” is “Right” “West” is “Left” N (Up) (Left) W E (Right) S (Down)

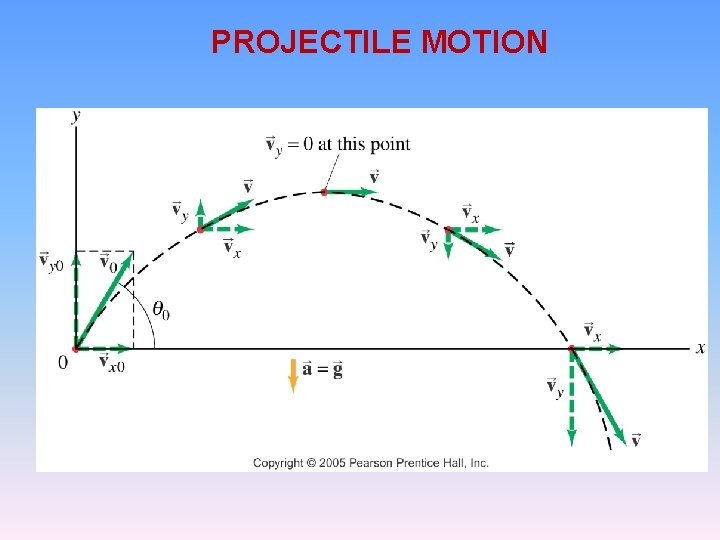
Projectile Motion A projectile is an object moving in two dimensions under the influence of Earth's gravity; its path is a parabola. Examples : a golf ball, a thrown or batted basketball, kicked footballs and speeding bullets.

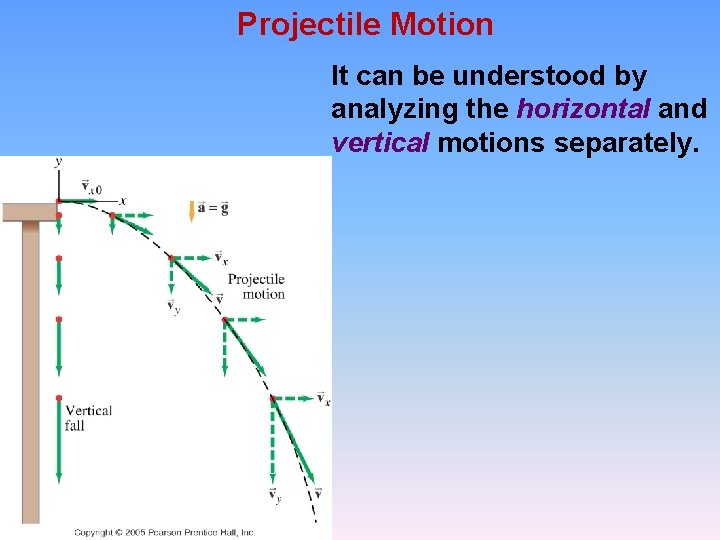
Projectile Motion It can be understood by analyzing the horizontal and vertical motions separately.

Projectile Motion The speed in the x-direction is constant; in the ydirection the object moves with constant acceleration g. This photograph shows two balls that start to fall at the same time. The on the right has an initial speed in the x-direction. It can be seen that vertical positions of the two balls are identical at identical times, while the horizontal position of the yellow ball increases linearly.

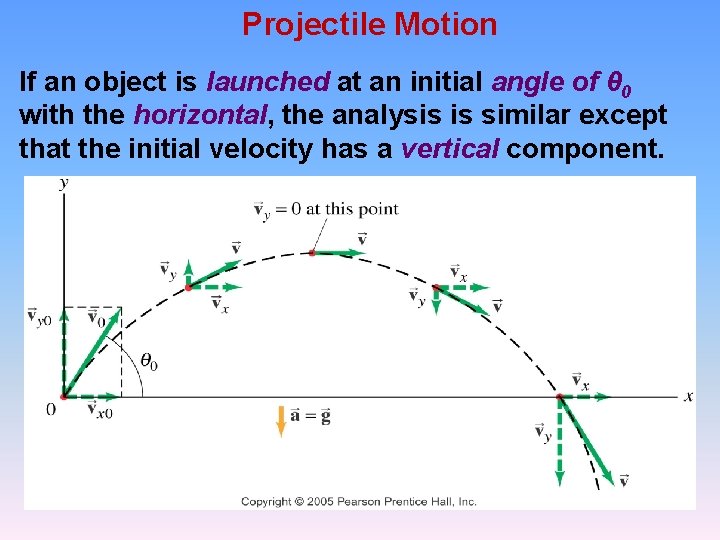
Projectile Motion If an object is launched at an initial angle of θ 0 with the horizontal, the analysis is similar except that the initial velocity has a vertical component.

Solving Problems Involving Projectile Motion Projectile motion is motion with constant acceleration in two dimensions, where the acceleration is g and is down.

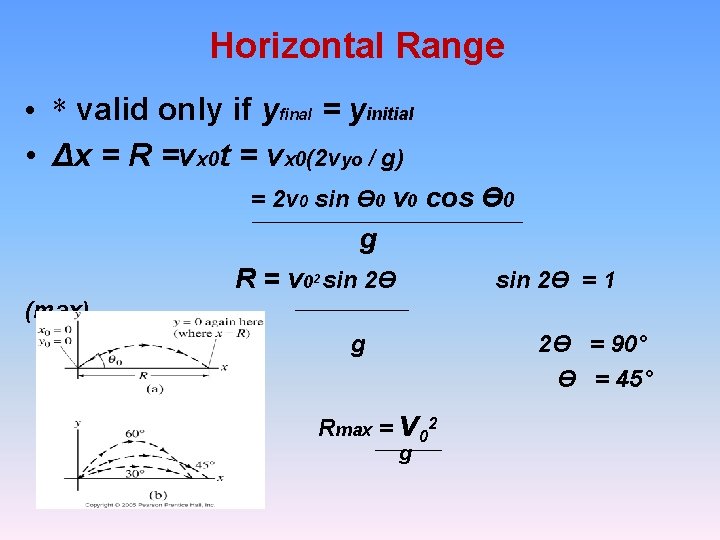
Special Equations • The motion equations can be combined algebraically and solved for the range and maximum height

Horizontal Range • * valid only if yfinal = yinitial • Δx = R =vx 0 t = vx 0(2 vyo / g) = 2 v 0 sin Ɵ 0 v 0 cos Ɵ 0 g R = v 02 sin 2Ɵ = 1 (max) g 2Ɵ = 90° Ɵ = 45° R max = v 02 g

Projectile Motion • An object may move in both the x and y directions simultaneously – It moves in two dimensions • The form of two dimensional motion we will deal with is an important special case called projectile motion Section 3. 4

Assumptions of Projectile Motion • We may ignore air friction • We may ignore the rotation of the earth • With these assumptions, an object in projectile motion will follow a parabolic path Section 3. 4

Rules of Projectile Motion • The x- and y-directions of motion are completely independent of each other • The x-direction is uniform motion – ax = 0 • The y-direction is free fall – ay = -g • The initial velocity can be broken down into its x- and y-components –

Projectile Motion Section 3. 4

Projectile Motion at Various Initial Angles • Complementary values of the initial angle result in the same range – The heights will be different • The maximum range occurs at a projection angle of 45 o Section 3. 4

Some Details About the Rules • x-direction • ax = 0 – x = voxt • This is the only operative equation in the xdirection since there is uniform velocity in that direction

More Details About the Rules • y-direction – – Free fall problem • a = -g – Take the positive direction as upward – Uniformly accelerated motion, so the motion equations all hold

Velocity of the Projectile • The velocity of the projectile at any point of its motion is the vector sum of its x and y components at that point – Remember to be careful about the angle’s quadrant

Projectile Motion Summary • Provided air resistance is negligible, the horizontal component of the velocity remains constant – Since ax = 0 • The vertical component of the acceleration is equal to the free fall acceleration –g – The acceleration in the y-direction is not zero at the top of the projectile’s trajectory

Projectile Motion Summary, cont • The vertical component of the velocity vy and the displacement in the y-direction are identical to those of a freely falling body • Projectile motion can be described as a superposition of two independent motions in the x- and y-directions

Problem-Solving Strategy • Select a coordinate system and sketch the path of the projectile – Include initial and final positions, velocities, and accelerations • Resolve the initial velocity into x- and ycomponents • Treat the horizontal and vertical motions independently

Problem-Solving Strategy, cont • Follow the techniques for solving problems with constant velocity to analyze the horizontal motion of the projectile • Follow the techniques for solving problems with constant acceleration to analyze the vertical motion of the projectile

Some Variations of Projectile Motion • An object may be fired horizontally • The initial velocity is all in the x-direction – vo = vx and vy = 0 • All the general rules of projectile motion apply

Non-Symmetrical Projectile Motion • Follow the general rules for projectile motion • Break the y-direction into parts – up and down – symmetrical back to initial height and then the rest of the height

Example: A Cap in the Air A delighted physics graduate throws her cap into the air with an initial velocity of 24. 5 m/s at a 36. 9° angle with the horizontal. The cap is later caught by another student. [Neglect air resistance ; Sin(36. 9°) = 3/5; Cos(36. 9°) = 4/5]. (a) Find the total time the cap is in the air. (b) Find the total horizontal distance traveled. g

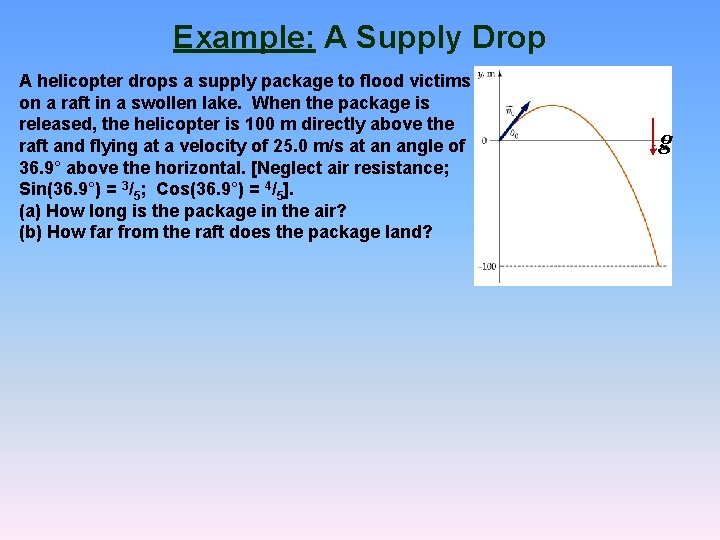
Example: A Supply Drop A helicopter drops a supply package to flood victims on a raft in a swollen lake. When the package is released, the helicopter is 100 m directly above the raft and flying at a velocity of 25. 0 m/s at an angle of 36. 9° above the horizontal. [Neglect air resistance; Sin(36. 9°) = 3/5; Cos(36. 9°) = 4/5]. (a) How long is the package in the air? (b) How far from the raft does the package land? g

Example: A Rough Shot Chipping from the rough, a golfer sends the ball over a 3. 0 m high tree that is 14. 0 m away. The ball lands on the green at the same level from which it was struck after traveling a horizontal distance of 17. 8 m. t 1 (a) If the ball left the club at 54. 0° above the horizontal and landed 2. 24 s later, what was its initial speed v 0? (b) How high was the ball when it passed over the tree?

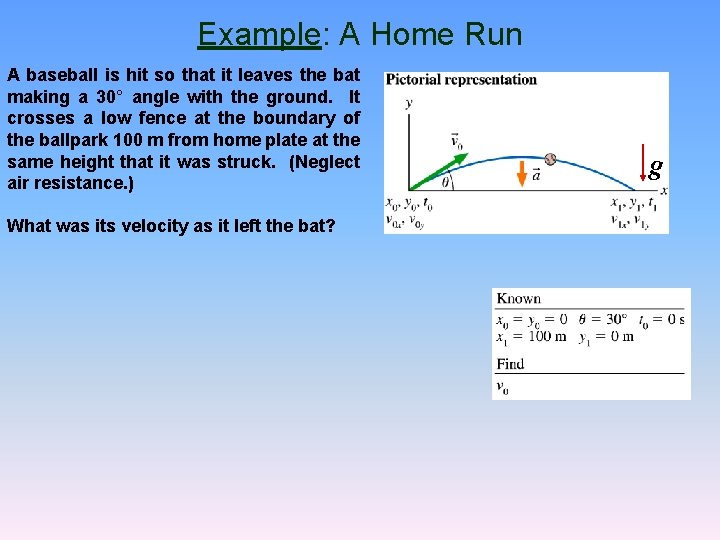
Example: A Home Run A baseball is hit so that it leaves the bat making a 30° angle with the ground. It crosses a low fence at the boundary of the ballpark 100 m from home plate at the same height that it was struck. (Neglect air resistance. ) What was its velocity as it left the bat? g

Example: An Elevated Green A golfer hits a ball from the origin with an initial speed of 30. 0 m/s at an angle of 50. 0° above the horizontal. The ball lands on a green that is 5. 00 m above the level where the ball was struck. (a) How long was the ball in the air? (b) How far did the ball travel horizontally before ot landed? (c) What is the speed and direction of the ball just before it lands?

Summary of Chapter 3 • A quantity with magnitude and direction is a vector. • A quantity with magnitude but no direction is a scalar. • Vector addition can be done either graphically or using components. v parallelogram method v tail-to-tip method • For subtract vectors, the negative vector is define has the same magnitude but points in the opposite direction • A vector can also be multiplied by a scalar and the result is different in magnitude but same direction

• If the scalar is negative, the resultant vector points in the opposite direction • Vectors can also be adding by components, (if the components are perpendicular, they can be found using trigonometric functions

PROJECTILE MOTION

THE END