Chapter 3 Kinematics in Two Dimensions 3 1

3. 1 Displacement, Velocity, and Acceleration

3. 1 Displacement, Velocity, and Acceleration Average velocity is the displacement divided by the

3. 1 Displacement, Velocity, and Acceleration The instantaneous velocity indicates how fast the car

3. 1 Displacement, Velocity, and Acceleration DEFINITION OF AVERAGE ACCELERATION

3. 2 Equations of Kinematics in Two Dimensions Equations of Kinematics

3. 2 Equations of Kinematics in Two Dimensions

3. 3 Projectile Motion Under the influence of gravity alone, an object near the

Example • A ball thrown horizontally from a 13 m high building strikes the

Solution • By definition, we have y = voyt – ½ gt 2 =

Problems to be solved • 3. 12, 3. 24, 3. 41, 3. 45, 3.

• B 3. 2 Some books advice serving a tennis ball at an

• B 3. 3 A tennis ball is served 2. 5 m above

Slides: 14

Download presentation

Chapter 3 Kinematics in Two Dimensions

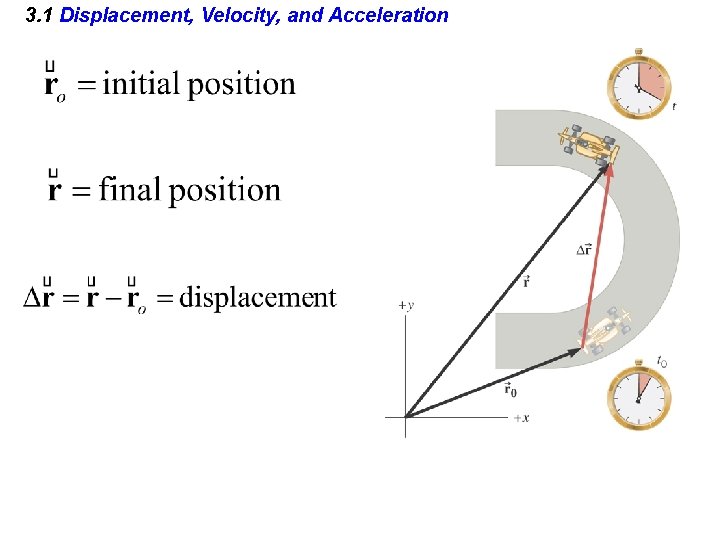
3. 1 Displacement, Velocity, and Acceleration

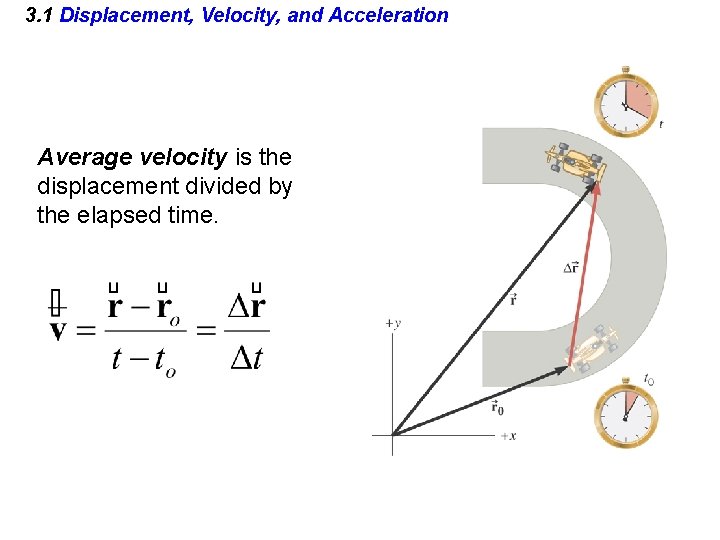
3. 1 Displacement, Velocity, and Acceleration Average velocity is the displacement divided by the elapsed time.

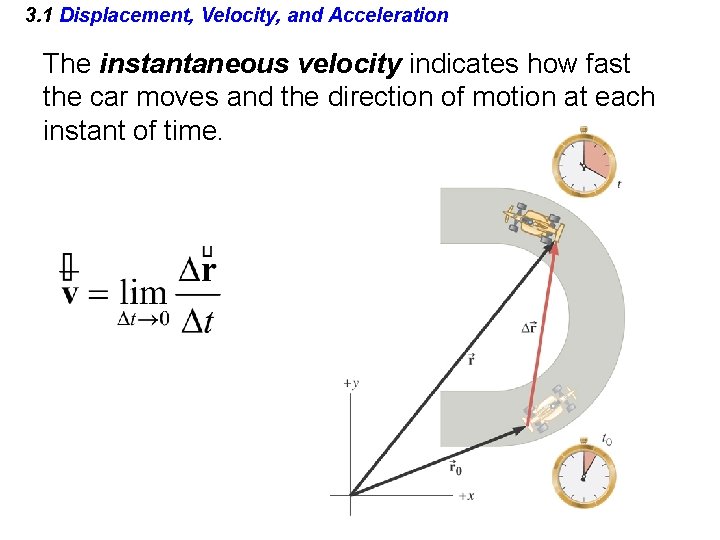
3. 1 Displacement, Velocity, and Acceleration The instantaneous velocity indicates how fast the car moves and the direction of motion at each instant of time.

3. 1 Displacement, Velocity, and Acceleration DEFINITION OF AVERAGE ACCELERATION

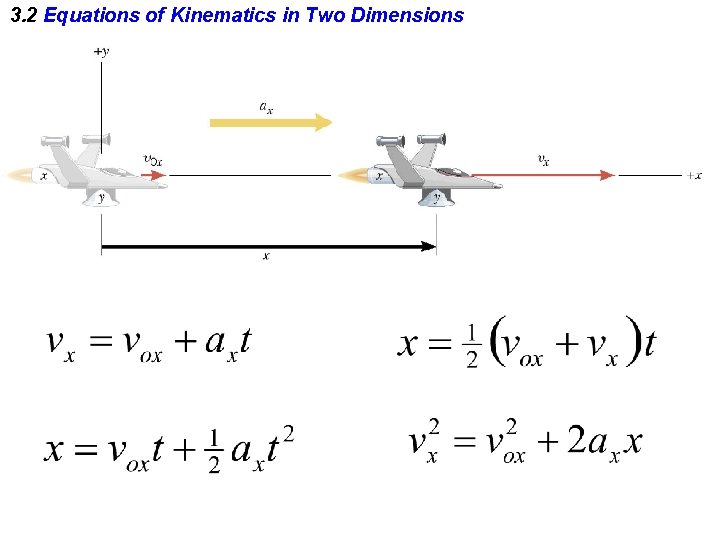
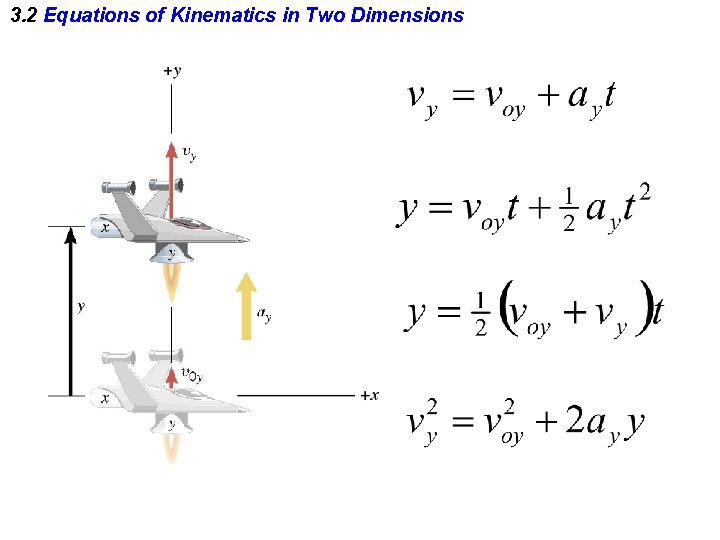
3. 2 Equations of Kinematics in Two Dimensions Equations of Kinematics

3. 2 Equations of Kinematics in Two Dimensions

3. 3 Projectile Motion Under the influence of gravity alone, an object near the surface of the Earth will accelerate downwards at 9. 80 m/s 2.

Example • A ball thrown horizontally from a 13 m high building strikes the ground 5. 0 m from the building. With what velocity was the ball thrown?

Solution • By definition, we have y = voyt – ½ gt 2 = -2 y/g = - [2×-13]/9. 8 = 2. 65 s 2 t = 1. 63 s Also, by definition we have x = voxt + ½ axt 2 vox = x/t = 5/1. 63 = 3. 07 m/s

Problems to be solved • 3. 12, 3. 24, 3. 41, 3. 45, 3. 51, 3. 72 • B 3. 1 A snowball is thrown from 2 m above the ground at a velocity of 10 m/s directed at 30° above the horizontal. (a)How long will the snowball be in the air? (b) Where will it land?

• B 3. 2 Some books advice serving a tennis ball at an angle below the horizontal direction. To see if this is sound advice, suppose a ball is struck at an angle of 5° downward at a height of 2. 4 m with the relatively high speed of 30 m/s. How high will it be when it reaches the net 12 m away? (The net is 0. 9 m high. Neglect air resistance. )

• B 3. 3 A tennis ball is served 2. 5 m above the ground at an angle of 5° above the horizontal direction with an initial speed of 30 m/s. (a) When will it hit the ground? (b) How far will it travel?