Chapter 3 Introduction to Algorithms Selection Sort 3

Chapter 3 – Introduction to Algorithms Selection Sort (3 slides) Selection Sort Alg. (3 slides) Search Algorithms (6 slides) Illustrating the Binary Search -Successful (3 slides) -Unsuccessful (3 slides) Binary Search Alg. (3 slides) Big-O Notation Constant Time Algorithms Linear Time Algorithms Exponential Algs. (2 slides) Logarithmic Time Algorithms 1 Main Index Selection Sort Algorithm -Integer Version -String Version Template Syntax (4 slides) Recursive Defn of the Power Fnc Stopping Conditions for. Recursive Algorithms Implementing the Recursive. Power Function Tower of Hanoi w/ Recursion (3 slides) Fibonacci Numbers Using. Iteration (2 slides) Summary Slides (5 slides) Contents

Selection Sort - 5 Element Array l l l 2 Pass 0: Scan the entire list from arr[0] to arr[4] and identify 20 at index 1 as the smallest element. Exchange 20 with arr[0] = 50, the first element in the list. Main Index Contents

Selection Sort - 5 Element Array l l l 3 Pass 1: Scan the sublist 50, 40, 75, and 35. Exchange the smallest element 35 at index 4 with arr[1] = 50. Main Index Contents

Selection Sort - 5 Element Array l l 4 Pass 2: Locate the smallest element in the sublist 40, 75, and 50. Main Index Contents

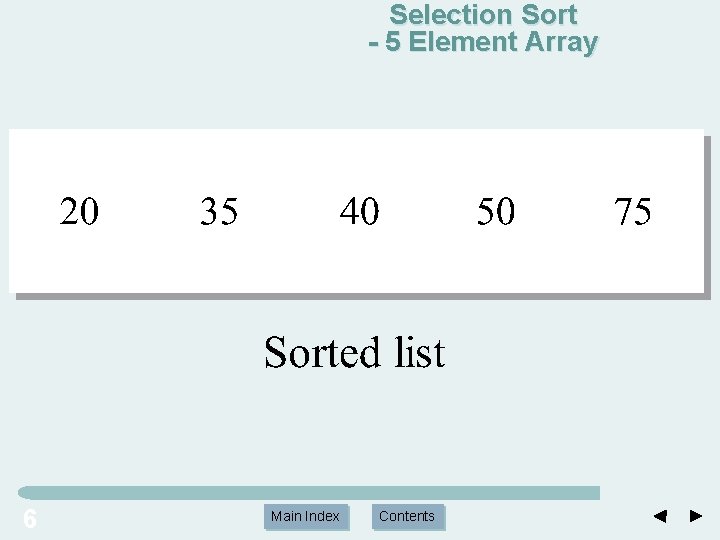
Selection Sort - 5 Element Array l l 5 Pass 3: Two elements remain to be sorted. Scan the sublist 75, 50 and exchange the smaller element with arr[3]. The exchange places 50 at index 4 in arr[3]. Main Index Contents

Selection Sort - 5 Element Array 6 Main Index Contents

Selection Sort Algorithm void selection. Sort(int arr[], int n) { int small. Index; // index of smallest // element in the sublist int pass, j; int temp; // pass has the range 0 to n-2 7 Main Index Contents

Selection Sort Algorithm for (pass = 0; pass < n-1; pass++) { // scan the sublist starting at index // pass small. Index = pass; // j traverses the sublist arr[pass+1] // to arr[n-1] for (j = pass+1; j < n; j++) // if smaller element found, assign // small. Index to that position 8 Main Index Contents

Selection Sort Algorithm if (arr[j] < arr[small. Index]) small. Index = j; // if small. Index and pass are not the // same location, exchange the // smallest item in the sublist with // arr[pass] if (small. Index != pass) { temp = arr[pass]; arr[pass] = arr[small. Index]; arr[small. Index] = temp; } } } 9 Main Index Contents

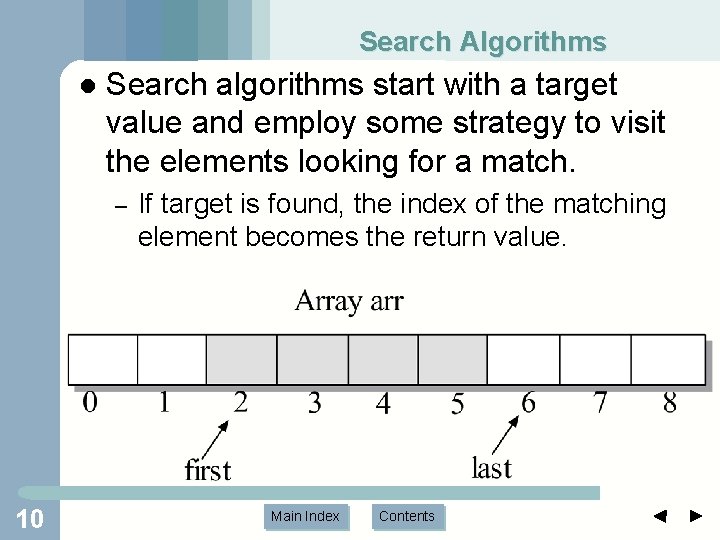
Search Algorithms l Search algorithms start with a target value and employ some strategy to visit the elements looking for a match. – 10 If target is found, the index of the matching element becomes the return value. Main Index Contents

Search Algorithms 11 Main Index Contents

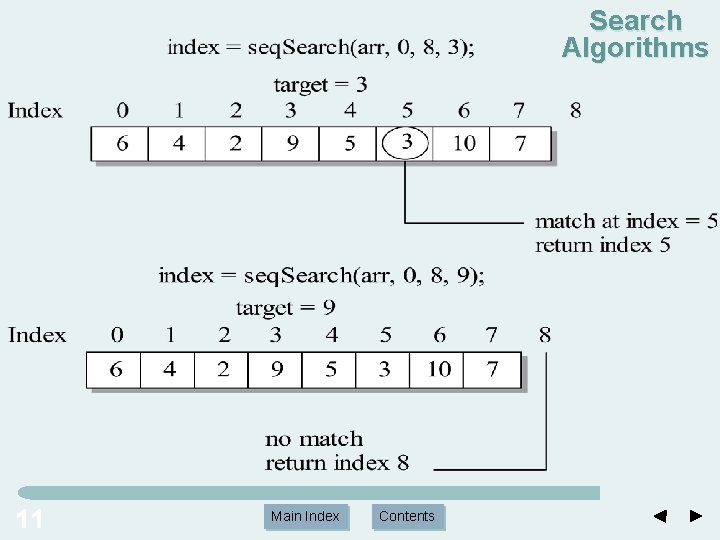
Search Algorithms - Sequential Search Algorithm int seq. Search(const int arr[], int first, int last, int target) { int i = first; // scan indices in the range first <= I < last; // test for a match or index out of range. while(i != last && arr[i] != target) i++; return i; // i is index of match or i = last if no match } 12 Main Index Contents

Search Algorithms Case 1. A match occurs. The search is complete and mid is the index that locates the target. if (mid. Value == target) // found match return mid; 13 Main Index Contents

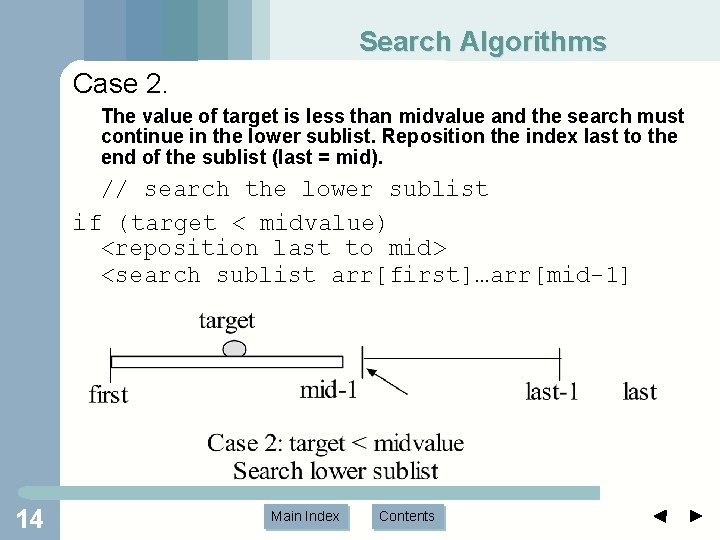
Search Algorithms Case 2. The value of target is less than midvalue and the search must continue in the lower sublist. Reposition the index last to the end of the sublist (last = mid). // search the lower sublist if (target < midvalue) <reposition last to mid> <search sublist arr[first]…arr[mid-1] 14 Main Index Contents

Search Algorithms Case 3. The value of target is greater than midvalue and the search must continue in the upper sublist. Reposition the index first to the front of the sublist (first = mid+1). // search upper sublist if (target > midvalue) <reposition first to mid+1> <search sublist arr[mid+1]…arr[last-1]> 15 Main Index Contents

Illustrating the Binary Search - Successful Search 1. Search for target = 23 Step 1: Indices first = 0, last = 9, mid = (0+9)/2 = 4. Since target = 23 > midvalue = 12, step 2 searches the upper sublist with first = 5 and last = 9. 16 Main Index Contents

Illustrating the Binary Search - Successful Search Step 2: Indices first = 5, last = 9, mid = (5+9)/2 = 7. Since target = 23 < midvalue = 33, step 3 searches the lower sublist with first = 5 and last = 7. 17 Main Index Contents

Illustrating the Binary Search - Successful Search Step 3: Indices first = 5, last = 7, mid = (5+7)/2 = 6. Since target = midvalue = 23, a match is found at index mid = 6. 18 Main Index Contents

Illustrating the Binary Search - Unsuccessful Search for target = 4. Step 1: Indices first = 0, last = 9, mid = (0+9)/2 = 4. Since target = 4 < midvalue = 12, step 2 searches the lower sublist with first = 0 and last = 4. 19 Main Index Contents

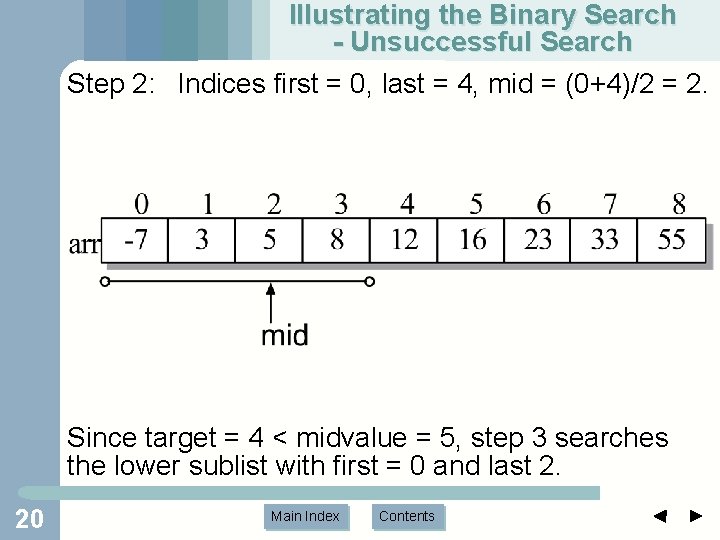
Illustrating the Binary Search - Unsuccessful Search Step 2: Indices first = 0, last = 4, mid = (0+4)/2 = 2. Since target = 4 < midvalue = 5, step 3 searches the lower sublist with first = 0 and last 2. 20 Main Index Contents

Illustrating the Binary Search - Unsuccessful Search Step 3: Indices first = 0, last = 2, mid = (0+2)/2 = 1. Since target = 4 > midvalue = 3, step 4 should search the upper sublist with first = 2 and last =2. However, since first >= last, the target is not in the list and we return index last = 9. 21 Main Index Contents

Binary Search Algorithm Int bin. Search(const int arr[], int first, int last, int target) { int mid; // index of the midpoint midvalue; // object that is // assigned arr[mid] int orig. Last = last; // save original value of last 22 Main Index Contents

Binary Search Algorithm while (first < last) // test for nonempty sublist { mid = (first+last)/2; midvalue = arr[mid]; if (target == midvalue) return mid; // have a match // determine which sublist to // search 23 Main Index Contents

Binary Search Algorithm else if (target < midvalue) last = mid; // search lower sublist. reset last else first = mid+1; // search upper sublist. Reset first } return orig. Last; // target not found } 24 Main Index Contents

Big-O notation ** Big-O notation provides a machine independent means for determining the efficiency of an Algorithm. For the selection sort, the number of comparisons is T(n) = n 2/2 - n/2. Entire expression is called the "Big-O" measure for the algorithm. n = 100: T(100) = 1002/2 -100/2 = 10000/2 - 100/2 = 5, 000 - 50 = 4, 950 25 Main Index Contents

Constant Time Algorithms An algorithm is O(1) when its running time is independent of the number of data items. The algorithm runs in constant time. The storing of the element involves a simple assignment statement and thus has efficiency O(1). 26 Main Index Contents

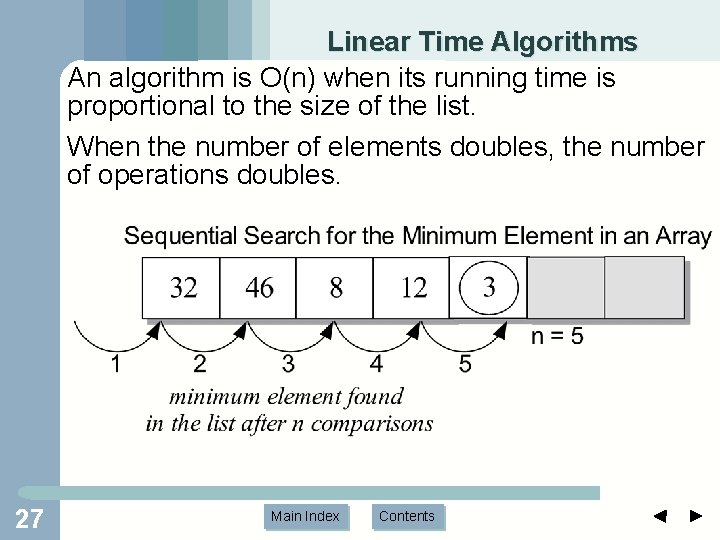
Linear Time Algorithms An algorithm is O(n) when its running time is proportional to the size of the list. When the number of elements doubles, the number of operations doubles. 27 Main Index Contents

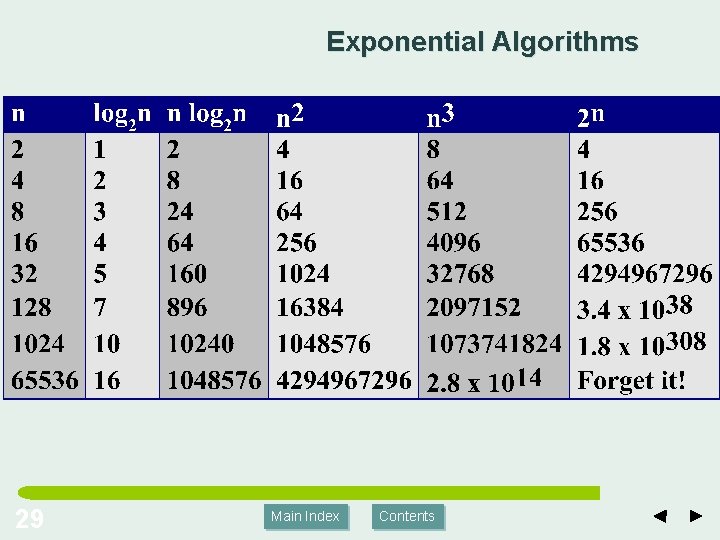
Exponential Algorithms with running time O(n 2) are quadratic. – practical only for relatively small values of n. l Whenever n doubles, the running time of the algorithm increases by a factor of 4. l Algorithms with running time O(n 3)are cubic. – 28 efficiency is generally poor; doubling the size of n increases the running time eight-fold. Main Index Contents

Exponential Algorithms 29 Main Index Contents

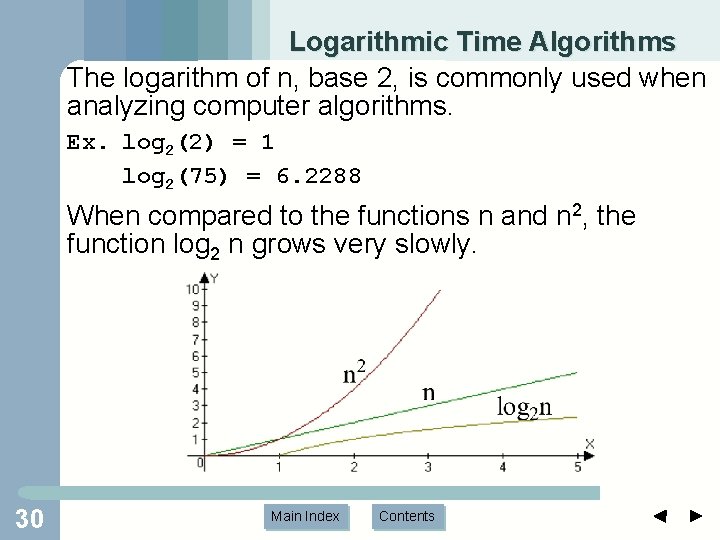
Logarithmic Time Algorithms The logarithm of n, base 2, is commonly used when analyzing computer algorithms. Ex. log 2(2) = 1 log 2(75) = 6. 2288 When compared to the functions n and n 2, the function log 2 n grows very slowly. 30 Main Index Contents

Selection Sort Algorithm Integer Version void selection. Sort(int arr[], int n) {. . . int temp; // int temp used for the exchange for (pass = 0; pass < n-1; pass++) {. . . if (arr[j] < arr[small. Index]) // compare integer elements. . . } } 31 Main Index Contents

Selection Sort Algorithm String Version void selection. Sort(string arr[], int n) { } 32 . . . string temp; // double temp used for the exchange for (pass = 0; pass < n-1; pass++) {. . . if (arr[j] < arr[small. Index]) // compare string element. . . } Main Index Contents

l l Template Syntax template function syntax includes the keyword template followed by a non-empty list of formal types enclosed in angle brackets. In the argument list, each type is preceded by the keyword typename, and types are separated by commas. // argument list with a multiple template // types template <typename T, typename U, typename V, . . . > 33 Main Index Contents

Template Syntax Example template <typename T> void selection. Sort(T arr[], int n) { int small. Index; // index of smallest element in the // sublist int pass, j; T temp; 34 Main Index Contents

Template Syntax Example // pass has the range 0 to n-2 for (pass = 0; pass < n-1; pass++) { // scan the sublist starting at // index pass small. Index = pass; // j traverses the sublist // a[pass+1] to a[n-1] for (j = pass+1; j < n; j++) // update if smaller element found 35 Main Index Contents

Template Syntax Example if (arr[j] < arr[small. Index]) small. Index = j; // if small. Index and pass are not // the same location, exchange the // smallest item in the sublist with // arr[pass] } 36 } if (small. Index != pass) { temp = arr[pass]; arr[pass] = arr[small. Index]; arr[small. Index] = temp; } Main Index Contents

l l Recursive Definition of the Power Function A recursive definition distinguishes between the exponent n = 0 (starting point) and n 1 which assumes we already know the value xn-1. After determining a starting point, each step uses a known power of 2 and doubles it to compute the next result. – l 37 Using this process gives us a new definition for the power function, xn. We compute all successive powers of x by multiplying the previous value by x. Main Index Contents

Stopping Conditions for Recursive Algorithms l Use a recursive function to implement a recursive algorithm. The design of a recursive function consists of 1. One or more stopping conditions that can be directly evaluated for certain arguments. – 2. One or more recursive steps in which a current value of the function can be computed by repeated calling of the function with arguments that will eventually arrive at a stopping condition. 38 Main Index Contents

Implementing the Recursive Power Function Recursive power(): double power(double x, int n) // n is a non-negative integer { if (n == 0) return 1. 0; // stopping condition else return x * power(x, n-1); // recursive step } 39 Main Index Contents

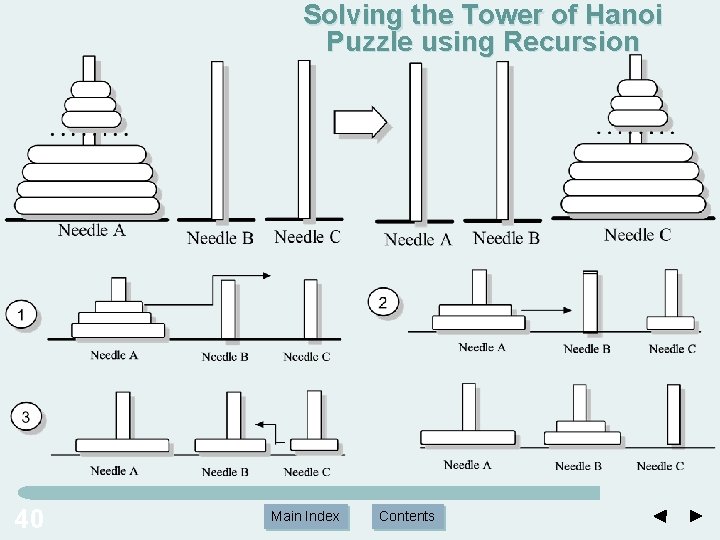
Solving the Tower of Hanoi Puzzle using Recursion 40 Main Index Contents

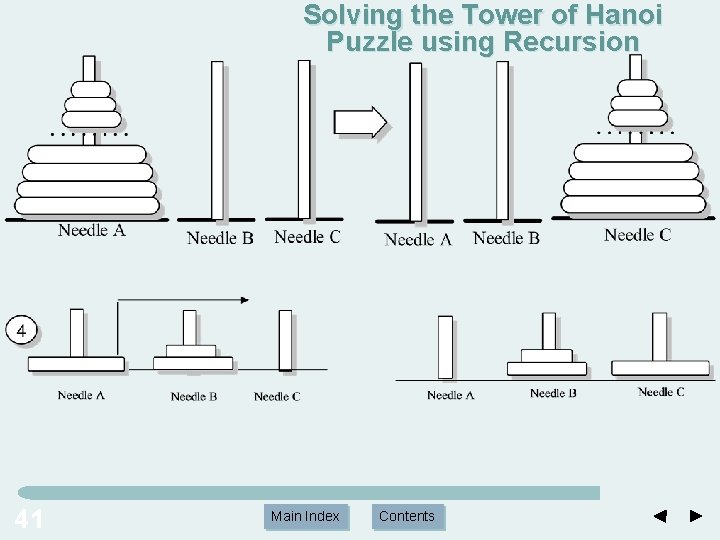
Solving the Tower of Hanoi Puzzle using Recursion 41 Main Index Contents

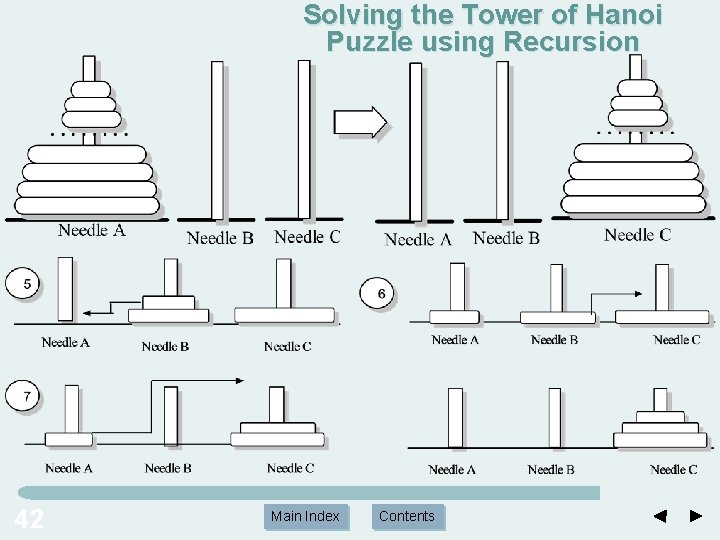
Solving the Tower of Hanoi Puzzle using Recursion 42 Main Index Contents

Fibonacci Numbers using Iteration int fibiter(int n) { // integers to store previous two Fibonacci value // int oneback = 1, twoback = 1, current; int i; // return is immediate for first two numbers if (n == 1 || n == 2) return 1; 43 Main Index Contents

Fibonacci Numbers using Iteration else // compute successive terms beginning at 3 for (i = 3; i <= n; i++) { current = oneback + twoback; twoback = oneback; // update for next calculation oneback = current; } return current; } 44 Main Index Contents

Summary Slide 1 §- The simplest form of searching is the sequential search. list. §- It compares the target with every element in a list until matching the target or reaching the end of the §- If the list is in sorted order, the binary search algorithm is more efficient. §- It exploits the structure of an ordered list to produce very fast search times. 45 Main Index Contents

Summary Slide 2 §- Big-O notation measures the efficiency of an algorithm by estimating the number of certain operations that the algorithm must perform. - For searching and sorting algorithms, the operation is data comparison. - Big-O measure is very useful for selecting among competing algorithms. 46 Main Index Contents

Summary Slide 3 §- The running time of the sequential search is O(n) for the worst and the average cases. §- The worst and average case for the binary search is O(log 2 n). §- Timing data obtained from a program provides experimental evidence to support the greater efficiency of the binary search. 47 Main Index Contents

Summary Slide 4 §- C++ provides a template mechanism that allows a programmer to write a single version of a function with general type arguments. - If a main program wants to call the function several times with different runtime arguments, the compiler looks at the types of the runtime arguments and creates different versions of the function that matches the types. 48 Main Index Contents

Summary Slide 5 §- An algorithm is recursive if it calls itself for smaller problems of its own type. §- Eventually, these problems must lead to one or more stopping conditions. - The solution at a stopping condition leads to the solution of previous problems. - In the implementation of recursion by a C++ function, the function calls itself. 49 49 Main Index Contents