CHAPTER 3 Information Theory and Coding 1 TOPICS

CHAPTER 3: Information Theory and Coding 1

TOPICS ¡ ¡ ¡ Probability Entropy and Information Mutual Information Channel Capacity Huffman Coding, Error detecting code, Error correcting code 2

3. 1 Probability -A probability experiment is something that can happen in more than one way. - --The Probability of an Event = P(Event) = the number of ways it can happen the number of possible outcomes

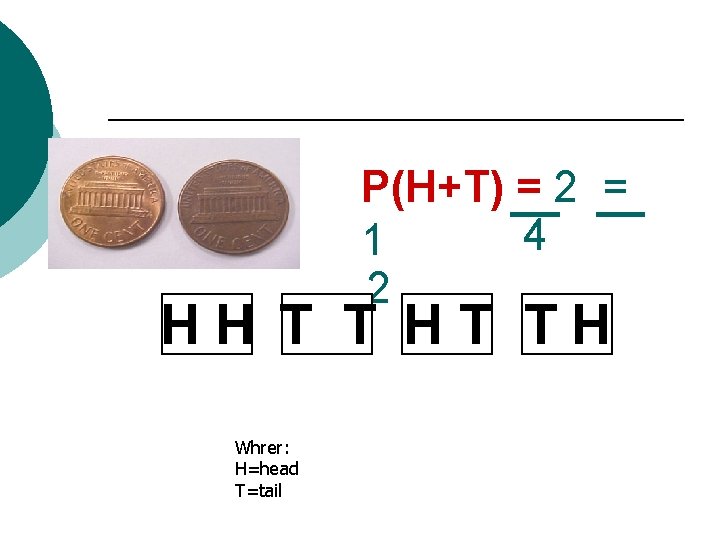
P(H+T) __ = 2 __ = 4 1 2 HH T T HT TH Whrer: H=head T=tail

What is the probability of rolling two coins and getting H first and then T? 1 4 P(H & then T) =

Information theory and entropy --Information theory tries to solve the problem of communicating as much data as possible over a noisy channel --Measure of data is entropy --Claude Shannon first demonstrated that reliable communication over a noisy channel is possible (jump-started digital age) 6

Entropy definitions ¡ Shannon entropy ¡ Binary entropy formula ¡ Differential entropy

Properties of entropy ¡ ¡ ¡ Can be defined as the expectation of log p(x) (ie (X) = E[-log p(x)]) Is not a function of a variable’s values, is a function of the variable’s probabilities Usually measured in “bits” (using logs of base 2) or “nats” (using logs of base e) Maximized when all values are equally likely (ie uniform distribution) Equal to 0 when only one value is possible Cannot be negative

3. 4 Channel Capacity Huffman Coding, Error detecting code, Error correcting code

Huffman Algorithm ¡ Construct a binary tree of codes l l l ¡ leaf nodes represent symbols to encode interior nodes represent cumulative probability edges assigned 0 or 1 output code Construct the tree bottom-up l connect the two nodes with the lowest probability until no more nodes to connect

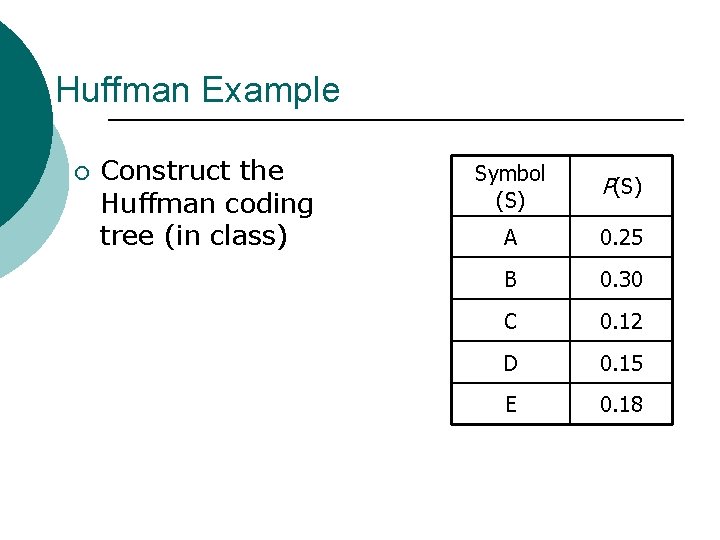
Huffman Example ¡ Construct the Huffman coding tree (in class) Symbol (S) P(S) A 0. 25 B 0. 30 C 0. 12 D 0. 15 E 0. 18

Characteristics of Solution ¡ ¡ Lowest probability symbol is always furthest from root Assignment of 0/1 to children edges arbitrary l l ¡ other solutions possible; lengths remain the same If two nodes have equal probability, can select any two Notes l l prefix free code O(nlgn) complexity Symbol (S) Code A 11 B 00 C 010 D 011 E 10

Example Encoding/Decoding Encode “BEAD” Þ 001011011 Þ Decode “ 0101100” Symbol (S) Code A 11 B 00 C 010 D 011 E 10