Chapter 3 Graphs and Functions 3 1 Graphs

Chapter 3 Graphs and Functions 3. 1 – Graphs 3. 2 – Functions 3. 3 – Linear Functions: Graphs and Applications 3. 4 – The Slope-Intercept Form of a Linear Equation 3. 5 – The Point-Slope Form of a Linear Equation 3. 6 – The Algebra of Functions 3. 7 – Graphing Linear Inequalities 1

3. 5 The Point-Slope Form of a Linear Equation Objectives: 1. Understand Point – Slope form of a Line 2. Recognize parallel & Perpendicular lines

Point-Slope Form Using the Point-Slope Form of the Equation of a Line To write the equation of a line given its slope and any point, (x 1, y 1), on the line, use the point-slope form of the equation of a line: y – y 1 = m(x – x 1). If given a second point (x 2, y 2), and not the slope, we first calculate the slope using then use y – y 1= m(x – x 1). Example 1: point (1, 4) and slope = -3:

Example 2 : • A line with a slope of 4 crosses the y-axis at the point (0, 5). Write the equation in slope–intercept form. In this case I would use y = mx + b y = 4 x + 5 • Solution • y – 5= 4(x – 0) y – 5= 4 x y = 4 x + 5

Example 3: • A line connects the points (2, 6) and (– 4, 3). Write the equation of the line in slope-intercept form. • Solution • Find the slope: • Use point-slope form: y – y 1 = m(x – x 1)

Example 4: • The following data points relate velocity of an object as time passes. The graph shows that the points are in a line. Write the equation of the line in slope-intercept and standard forms. Time (x) (in seconds) Velocity (y) (in ft. /sec. ) 0 4. 5 1 6 2 7. 5 3 10. 5 • Find the slope: • use (0, 4. 5) and (1, 6).

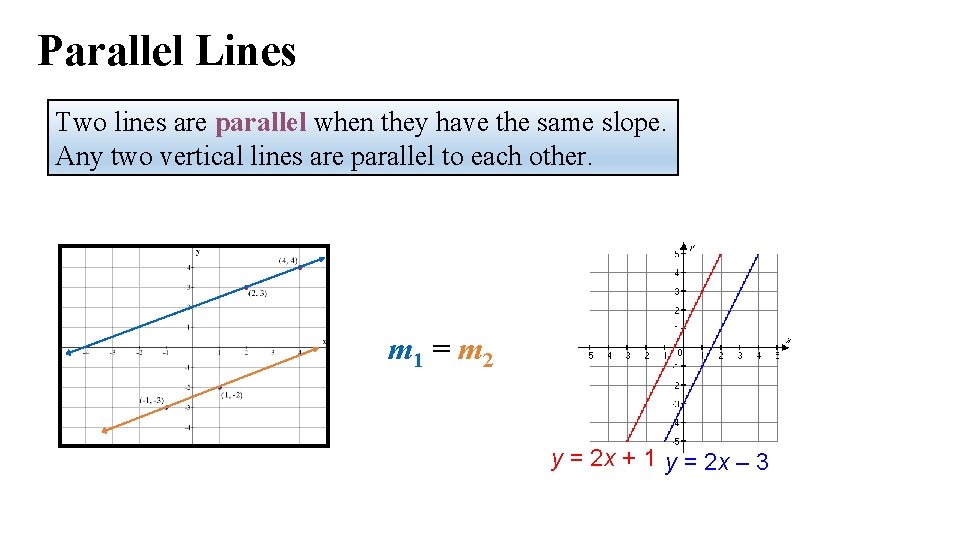
Parallel Lines Two lines are parallel when they have the same slope. Any two vertical lines are parallel to each other. m 1 = m 2 y = 2 x + 1 y = 2 x – 3

Example 4: • Write the equation of a line that passes through (1, – 5) and parallel to • y = – 3 x + 4. Write the equation in slope-intercept form. • Solution m 1 = m 2= – 3 • • y – y 1 = m(x – x 1) y – ( 5) = – 3(x – 1) y + 5 = – 3 x + 3 y = – 3 x – 2

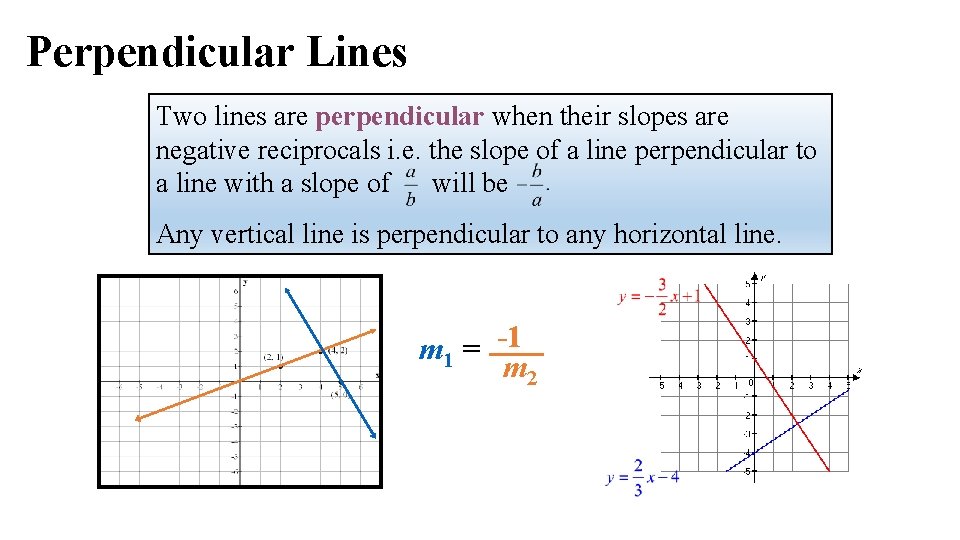
Perpendicular Lines Two lines are perpendicular when their slopes are negative reciprocals i. e. the slope of a line perpendicular to a line with a slope of will be Any vertical line is perpendicular to any horizontal line. m 1 = -1 m 2

Example 5: • Write the equation of a line that passes through (7, 1) and is perpendicular to 7 x – 2 y = – 2. Write the equation in slopeintercept form. • Solution • Determine the slope of the line 7 x – 2 y = – 2. • Slope of perpendicular line: •

Example 6: • Determine whether the given lines are parallel, perpendicular, or neither. • Solution • the lines are perpendicular.