Chapter 3 Graphing Linear Functions Sec 3 1

Chapter 3 Graphing Linear Functions Sec 3. 1 Functions

Relation - A pairing of inputs with outputs • Can be listed as a set of ordered pairs x-coordinate - An input • First number in an ordered pair y-coordinate - An output • Second number in an ordered pair Function - A relation that pairs each input with exactly one output Functions can be described • By an equation • Using words • By an input-output table • By a graph • By a mapping • As a set of ordered pairs

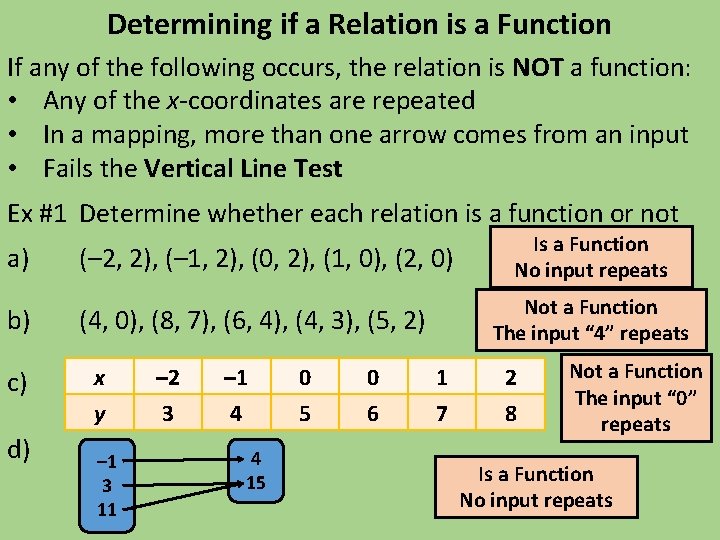
Determining if a Relation is a Function If any of the following occurs, the relation is NOT a function: • Any of the x-coordinates are repeated • In a mapping, more than one arrow comes from an input • Fails the Vertical Line Test Ex #1 Determine whether each relation is a function or not a) b) c) d) (– 2, 2), (– 1, 2), (0, 2), (1, 0), (2, 0) Not a Function The input “ 4” repeats (4, 0), (8, 7), (6, 4), (4, 3), (5, 2) x y – 1 3 11 – 2 3 – 1 4 4 15 0 6 Is a Function No input repeats 1 7 2 8 Not a Function The input “ 0” repeats Is a Function No input repeats

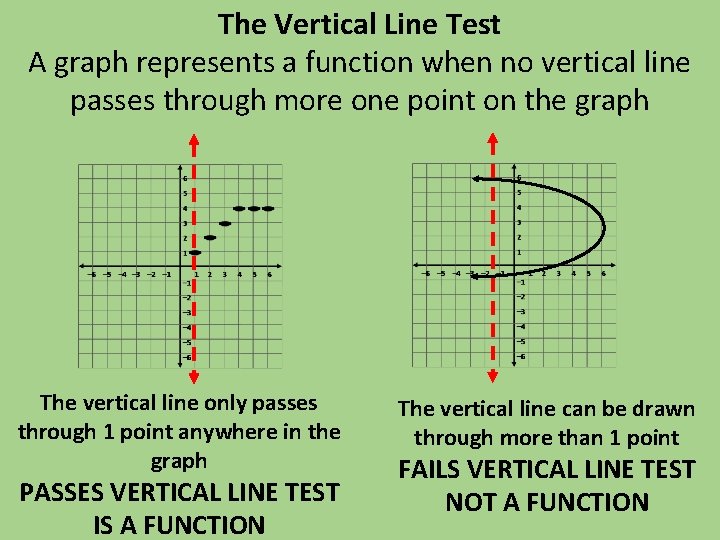
The Vertical Line Test A graph represents a function when no vertical line passes through more one point on the graph The vertical line only passes through 1 point anywhere in the graph PASSES VERTICAL LINE TEST IS A FUNCTION The vertical line can be drawn through more than 1 point FAILS VERTICAL LINE TEST NOT A FUNCTION

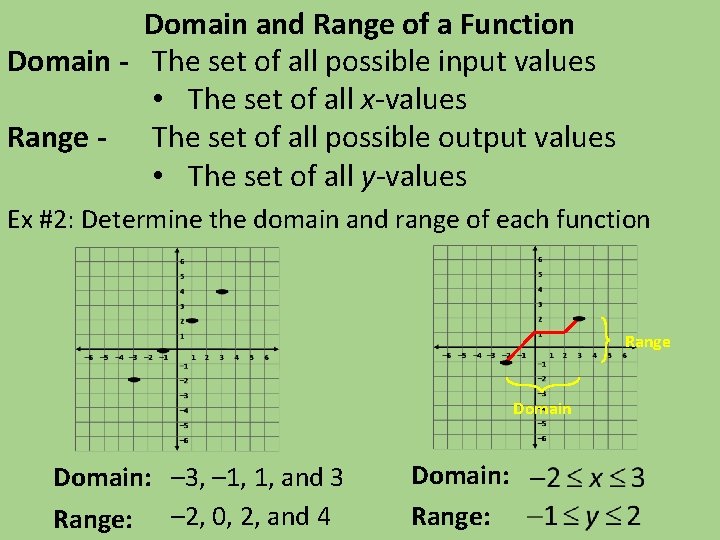
Domain and Range of a Function Domain - The set of all possible input values • The set of all x-values Range - The set of all possible output values • The set of all y-values Ex #2: Determine the domain and range of each function Range Domain: – 3, – 1, 1, and 3 Range: – 2, 0, 2, and 4 Domain: Range:

Identifying Independent and Dependent Variables Independent Variable - The variable that represents the input values of a function Dependent Variable - The variable that represents the output values of a function Ex #3 Given the function a = – 4 b +14 represents the number of a avocados you have left after making b batches of guacamole. Because the number a of avocados left depends on the amount of b batches of guacamole made: b is the independent variable a is the dependent variable

Ex #4 The function y = – 3 x +12 represents the amount y (in fluid ounces) of juice remaining in a bottle after you take x gulps. Find the range when the domain is 0, 1, 2, 3, and 4. Input, x – 3 x +12 Output, y 0 – 3(0) +12 12 1 – 3(1) +12 9 2 – 3(2) +12 6 3 – 3(3) +12 3 4 – 3(4) +12 0 The range is 12, 9, 6, 3, and 0