Chapter 3 Graphing Linear Equations Section 3 Slope

Chapter 3 Graphing Linear Equations Section 3 Slope of a Line Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 1

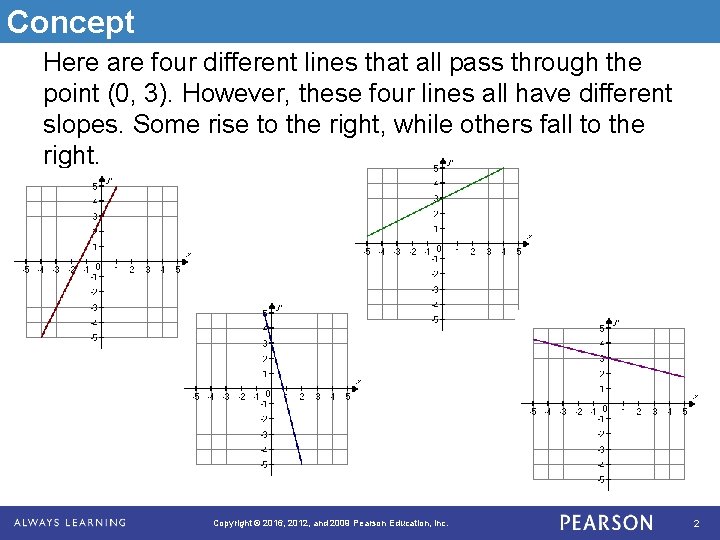
Concept Here are four different lines that all pass through the point (0, 3). However, these four lines all have different slopes. Some rise to the right, while others fall to the right. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 2

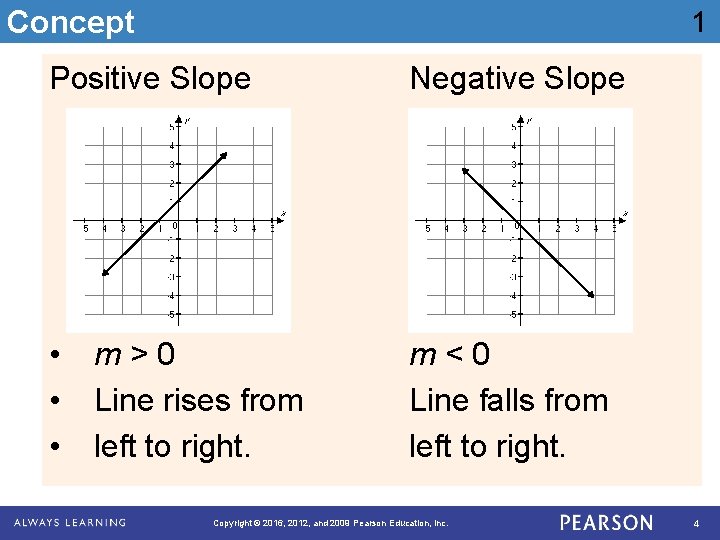
Concept Slope The slope of a line, m, is a measure of how steeply a line rises or falls as it moves to the right. If a line rises as it moves to the right, then its slope is positive. If a line falls as it moves to the right, then its slope is negative. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 3

Concept 1 Positive Slope Negative Slope • • • m<0 Line falls from left to right. m>0 Line rises from left to right. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 4

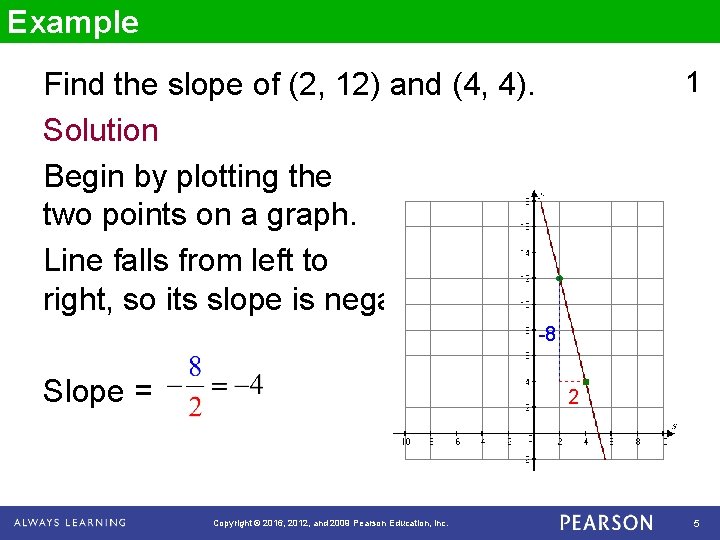
Example 1 Find the slope of (2, 12) and (4, 4). Solution Begin by plotting the two points on a graph. Line falls from left to right, so its slope is negative. -8 Slope = 2 Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 5

Concept 2 Slope Formula If a line passes through two points and then we can calculate its slope using the formula Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 6

Example 3 Slope Formula Find the slope of the line that passes through the two points: Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 7

Concept Slope of a Horizontal or Vertical Line 4 The slope of a horizontal line is 0. The slope of a vertical line is undefined. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 8

Example Slope of a Horizontal or Vertical Line Find the slope of the line: The line is horizontal, so Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 9

Example Slope of a Horizontal or Vertical Line Find the slope of the line: The line is vertical, so its slope is undefined. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 10

Concept Slope-Intercept Form of a Line The equation of a line is in slope-intercept form if it is written in the form The coefficient of x is the slope m, while b represents the y-coordinate of the y-intercept. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 11

Example 5 Slope-Intercept Form of a Line Find the slope and y-intercept of the line: The slope is and the y-intercept is Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 12

Example 6 Slope-Intercept Form of a Line Find the slope and y-intercept of the line: The slope is and the y-intercept is Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 13

Concept Graphing a Line Using Its Slope and y-Intercept First plot the y-intercept. Then use the slope of the line to find a second point. Draw a line that passes through these two points. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 14

Example 7 Graphing a Line Using Its Slope and y-Intercept Graph: y-intercept: Slope: 4 (Up 4 units, 1 to the right) Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 15

Example 8 The number of Americans (y), in millions, who have a cellular phone can be approximated by the equation y = 13 x + 77, where x is the number of years after 1999. Interpret the slope and y-intercept of this line. Solution The slope of the line is 13, and this tell us that each year we can expect an additional 13 million Americans to have a cellular phone. The y-intercept at (0, 77) tells us that approximately 77 million Americans had a cellular phone in 1999. Copyright © 2016, 2012, and 2009 Pearson Education, Inc. 16