Chapter 3 Functional Programming Outline n Introduction to

Chapter 3 Functional Programming

Outline n Introduction to functional programming n Scheme: an untyped functional programming language

Storage vs. Value n In imperative languages, stroage is visible: q q n variables are names of storage cells. assignment changes the value in a storage cell. explicit allocation and deallocation of storage. computation is a sequence of updates to storage. Functional languages manipulates values, rather than storage. There is no notion of storage in functional languages. q variables are names of values.

Assignment vs. Expression n In pure functional programming, there is no assignment and each program (or function) is an expression. v == 0 ? u : gcd(v, u % v); (define gcd (lambda (u v) (if (= v 0) u (gcd v (remainder u v)) )

Referential Transparency n Due to the lack of assignment, the value of a function call depends only on the values of its arguments. gcd(9, 15) n n There is no explicit notion of state. This property makes the semantics of functional programs particularly simple.

Loops vs. Recursion n n Due to the lack of assignment, repetition cannot be carried out through loops. A loop must have a control variable that is reassigned as the loop executes. Repetition is carried out through recursion in functional languages.

Functions as Values n n n In functional languages, functions are viewed as values. They can be manipulated in arbitrary ways without arbitrary restrictions. Functions can be created and modified dynamically during computation. Functions are first-class values.

Higher-Order Functions n n As other first-class values, functions can be passed as arguments and returned as values. A function is called a higher-order function if it has function parameters or returns functions.

Scheme: A Dialect of Lisp n n n The development of Lisp begins in 1958. Lisp is based on the lambda calculus. Lisp was called Lisp (List processor) because its basic data structure is a list. Unfortunately, no single standard evolved for the Lisp language, and many different dialects have been developed over the years. Scheme is one of the dialects of Lisp.

Starting Scheme n n n We will use the MIT Scheme interpreter to illustrate the features of Scheme. When we start the MIT Scheme interpreter, we will enter the Read-Eval-Print Loop (REPL) of the interpreter. It displays a prompt whenever it is waiting for your input. You then type an expression. Scheme evaluates the expression, prints the result, and gives you a prompt.

An Example 1 ]=> 12 ; Value: 12 1 ]=> foo ; Unbound variable: foo ; To continue, call RESTART with an option number: ; (RESTART 3) => Specify a value to use instead. . . ; (RESTART 2) => Define foo to a given value. ; (RESTART 1) => Return to read-eval-print level 1. 2 error>

Leaving Scheme n You can leave Scheme by calling the procedure exit. 1 ]=> (exit) Kill Scheme (y or n)? y

Scheme Syntax n The syntax of Scheme is particularly simple: expression atom | list atom number | string | identifier | character | boolean list ‘(’ expression-sequence ‘)’ expression-sequence | expression

Some Examples 42 “hello” hello #a #t (2. 1 2. 2 2. 3) (+ 2 3) a number a string an identifier a character the Boolean value “true” a list of numbers a list consisting of an identifier “+” and two numbers

Scheme Semantics n n n A constant atom evaluates to itself. An identifier evaluates to the value bound to it. A list is evaluated by recursively evaluating each element in the list as an expression (in some unspecified order); the first expression in the list evaluates to a function. This function is then applied to the evaluated values of the rest of the list.

Some Examples 1 ]=> 42 1 ]=> #t ; Value: 42 ; Value: #t 1 ]=> “hello” 1 ]=> (+ 2 3) ; Value 1: “hello” ; Value: 5 1 ]=> #a 1 ]=> (* (+ 2 3) (/ 6 2)) ; Value: #a ; Value: 15

Numerical Operations n The following are type predicates: (number? x) (complex? x) (real? x) (rational? x) (integer? x) ; (number? 3+4 i) ; (complex? 3+4 i) ; (real? -0. 25) ; (rational? 6/3) ; (integer? 3. 0)

Numerical Operations n The following are relational operators: (= x y z …) (< x y z …) (> x y z …) (<= x y z …) (>= x y z …)

Numerical Operations n The following are more predicates: (zero? x) (positive? x) (negative? x) (odd? x) (even? x)

Numerical Operations n The following are arithmetic operators: (+ x …) (* x …) (- x …) (/ x …) (max x y …) (min x y …) ; (+ 3 4 5) ; (* 3 4 5) ; (- 3 4 5) ; (/ 3 4 5) ; (max 3 4 5) ; (min 3 4 5)

Numerical Operations n The following are arithmetic operators: quotient abs gcd ceiling exp remainder numerator lcm truncate log modulo denominator floor round sqrt

Boolean Operations n The following are boolean operations: (boolean? x) (not x) (and x …) (or x …) ; (boolean? #f) ; (not 3) ; (and 3 4 5) ; (or 3 4 5)

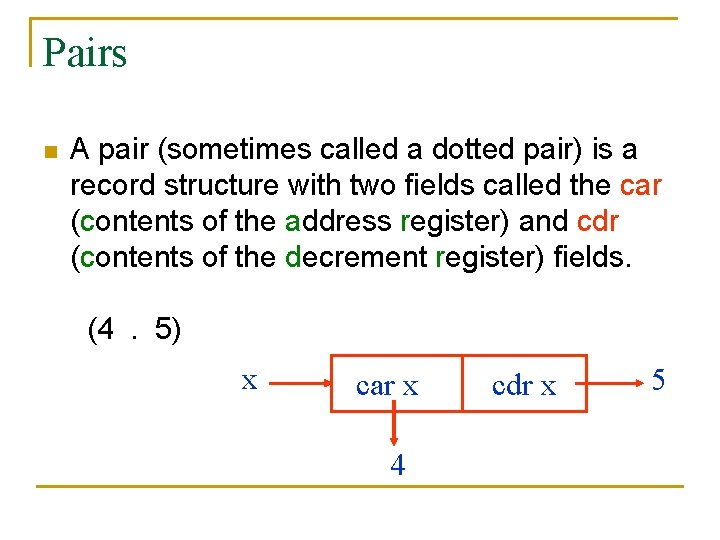
Pairs n A pair (sometimes called a dotted pair) is a record structure with two fields called the car (contents of the address register) and cdr (contents of the decrement register) fields. (4. 5) x car x 4 cdr x 5

Lists n Pairs are used primarily to represent lists. A list is an empty list or a pair whose cdr is a list () (a. ()) (a. (b. ())) ; (a) ; (a b)

Literal Expressions n (quote x) evaluates to x. (quote a) (quote (+ 1 2)) n ; a ; (+ 1 2) (quote x) may be abbreviated as ‘x. ‘a ‘(+ 1 2) ; a ; (+ 1 2)

List Operations n n n (cons x y) ; return a pair whose car is x and cdr is y (cons ‘a ‘(b c)) ; (a b c) (cons ‘(a) ‘(b c)) ; ((a) b c) (car x) ; return the car field of x (car ‘(a b c)); a (car ‘((a) b c)) ; (a) (cdr x) ; return the cdr field of x (cdr ‘(a b c)); (b c) (cdr ‘((a) b c)) ; (b c)

List Operations n n n n (caar x) (cadr x) (pair? x) (null? x) (length x) (list x …) (append x …) (reverse x) ; (caar ‘((a) b c)) ; (cadr ‘((a) b c)) ; (pair? ‘(a b c)) ; (null? ‘(a b c)) ; (length ‘(a b c)) ; (list ‘a ‘b ‘c) ; (append ‘(a) ‘(b) ‘(c)) ; (reverse ‘(a b c))

Conditionals n n (if test consequent) (if test consequent alternate) (if (> 3 2) ‘yes ‘no) (if (> 3 2) (- 3 2) (+ 3 2)) Special form Evaluation of arguments are delayed

Conditionals n (cond (test 1 expr 1 …) (test 2 expr 2 …) … (else expr …)) (cond ((> 3 2) ‘greater) ((< 3 2) ‘less) (else ‘equal))

Function Definition n Functions can be defined using the function define (variable formals) body) (define (gcd u v) (if (= v 0) u (gcd v (remainder u v)) ) )

An Example (append ‘(1 2 3) ‘(4 5 6)) ; (1 2 3 4 5 6) (define (append x y) (if (null? x) y (cons (car x) (append (cdr x) y)) ) )

An Example (reverse ‘(1 2 3)) ; (3 2 1) (define (reverse x) (if (null? x) x (append (reverse (cdr x)) (cons (car x) ‘())) ) )

Tail Recursion n n A recursion is called tail recursion if the recursive call is the last operation in the function definition. (define (gcd u v) (if (= v 0) u (gcd v (remainder u v)) ) ) Scheme compiler or interpreter will optimize a tail recursion into a loop.

An Example (define (reverse x) (if (null? x) x (append (reverse (cdr x)) (cons (car x) ‘())) ) ) (define (reverse x) (reverse 1 x ‘())) (define (reverse 1 x y) Accumulator (if (null? x) y (reverse 1 (cdr x) (cons (car x) y))) ) )

Lambda Expressions n The value of a function is represented as a lambda expression. (define (square x) (* x x)) (define square (lambda (x) (* x x))) n A lambda expression is also called an anonymous function

An Example (define gcd (lambda (u v) (if (= v 0) u (gcd v (remainder u v)) )

Higher-Order Functions n The procedure (apply proc args) calls the procedure proc with the elements of args as the actual arguments. Args must be a list. (apply + ‘(3 4)) ; 7 (apply (lambda (x) (* x x)) ‘(3)) ; 9

Higher-Order Functions n The procedure (map proc list 1 list 2 …) applies the procedure proc element-wise to the elements of the lists and returns a list of the results. (map cadr ‘((a b) (d e) (g h))) ; (b e h) (map (lambda (x) (* x x)) ‘(1 2 3)) ; (1 4 9)

Higher-Order Functions n An example of returning lambda expressions is as follows: (define (make-double f) (lambda (x) (f x x))) (define square (make-double *)) (square 2)

Equivalence Predicates n (eqv? obj 1 obj 2) returns #t if obj 1 and obj 2 are the same object (eqv? ‘a ‘a) (eqv? (cons 1 2) n (equal? obj 1 obj 2) returns #t if obj 1 and obj 2 print the same (equal? ‘a ‘a) (equal? (cons 1 2)

Input and Output n n the function reads a representation of an object from the input and returns the object (read) the function writes a representation of an object to the output (write object)

Load Programs n Functions and expressions in a file can be loaded into the system via the function load (load filename) (load “C: \user\naiwei\ex. txt”)