CHAPTER 3 FOURIER SERIES REPRESENTATION OF PERIODIC SIGNALS























![Example 3. 8 Consider the signal x[n] = sin 3(2π/5)n, draw the graph of Example 3. 8 Consider the signal x[n] = sin 3(2π/5)n, draw the graph of](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-30.jpg)




![1 … -5 x 1[n] … 0 5 x 2[n] 1 … -5 n 1 … -5 x 1[n] … 0 5 x 2[n] 1 … -5 n](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-37.jpg)
![Example 3. 11 Giving the following facts about a sequence x[n]: 1. x[n] is Example 3. 11 Giving the following facts about a sequence x[n]: 1. x[n] is](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-38.jpg)


![In discrete time, let x[n] be a periodic signal with Fourier series representation given In discrete time, let x[n] be a periodic signal with Fourier series representation given](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-41.jpg)

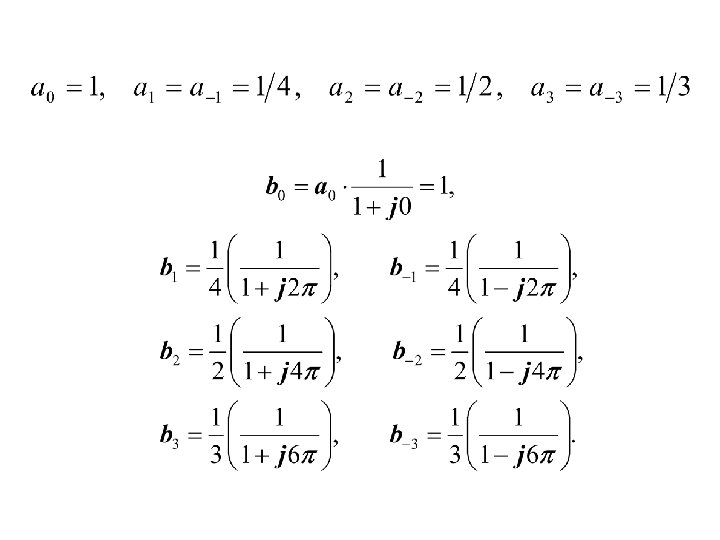



- Slides: 46

CHAPTER 3 FOURIER SERIES REPRESENTATION OF PERIODIC SIGNALS 3. 0 INTRODUCTION • Representation of continuous-time and discretetime periodic signals — Fourier series(傅立叶 级数). • Use Fourier methods to analyze and understand signals and LTI systems.

3. 1 THE RESPONSE OF LTI SYSTEMS TO COMPLEX EXPONENTIALS Ø Important concept — signal decomposition n basic signals: possess two properties 1. The set of basic signals can be used to construct a broad and useful class of signals. 2. It should be convenient for us to represent the response of an LTI system to any signal constructed as a linear combination of the basic signals. n complex exponential signals in continuous time: in discrete time:

Eigenfunction(特征函数) ØDefining two quantities: H(s) and H(z) Ø H(s) or H(z) is in general a function of the complex variable s or z. ØEigenfunction( of the system): an input signal for which the system output is a constant times the input. For a specific value of sk or zk , or : eigenvalue. (特征值)

ØIf the input to a continuous (discrete) time LTI system is represented as a linear combination of complex exponentials: then from the eigenfunction property and the superposition property, the output will be:

3. 2 FOURIER SERIES REPRESENTATION OF CONTINUOUS-TIME PERIODIC SIGNALS 3. 2. 1 Complex Exponential Fourier Series(指数型傅立叶级数) Given periodic x(t) with fundamental period T , its complex exponential Fourier series is : where the coefficients ak is generally a complex function of. The signals in the set are harmonically related complex exponentials. : fundamental components or the first harmonic components (基波分量) (一次谐波分量) the Nth harmonic components( N次谐波分量)

the Fourier series coefficients are determined by equation: synthesis equation: analysis equation: Fourier series coefficients or spectrum of x(t): (傅立叶系数) (频谱) magnitude spectrum: phase spectrum: (幅度频谱) (相位频谱) constant component or dc of x(t): (直流分量)

3. 2. 2 Trigonometric Fourier Series (三角型傅立叶级数) or The relationships between ak and Bk, Ck, Ak, θk are:

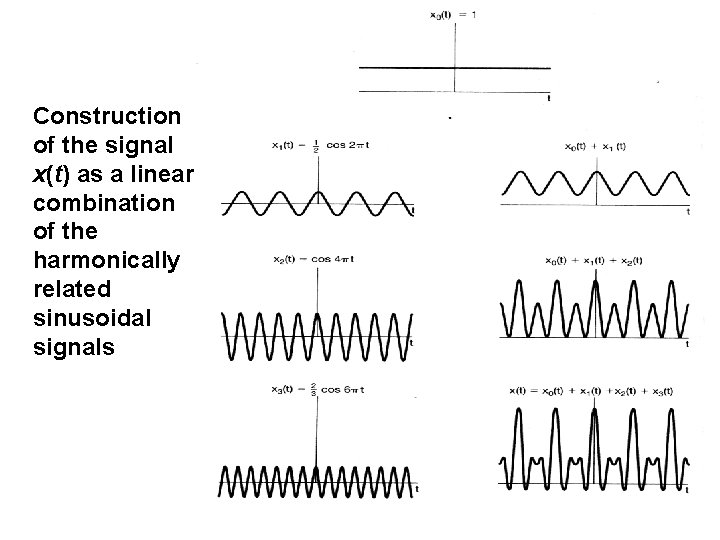
Construction of the signal x(t) as a linear combination of the harmonically related sinusoidal signals

Example 3. 1 Consider a real periodic signal x(t), with fundamental frequency 2π, that is expressed in the complex exponential Fourier series as where Use the trigonometric form to express the signal x(t).

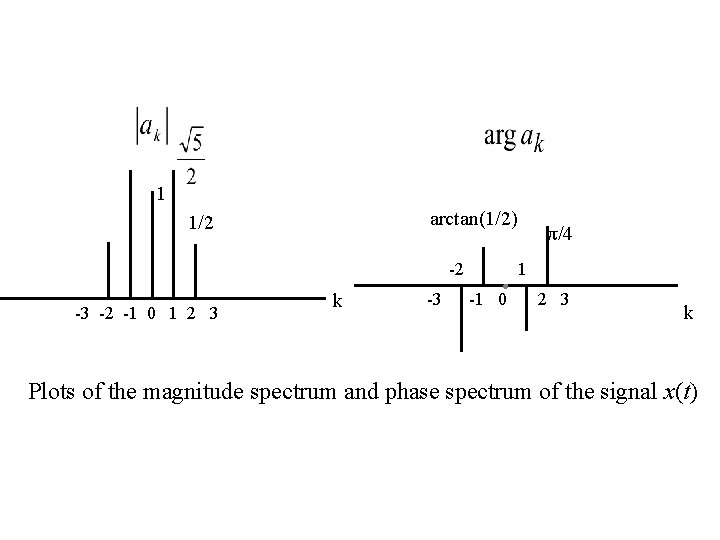
Example 3. 2 Consider the signal Plot the magnitude spectrum and phase spectrum of x(t). Thus, the Fourier series coefficients for this example are :

1 arctan(1/2) 1/2 -2 -3 -2 -1 0 1 2 3 k -3 π/4 1 -1 0 2 3 k Plots of the magnitude spectrum and phase spectrum of the signal x(t)

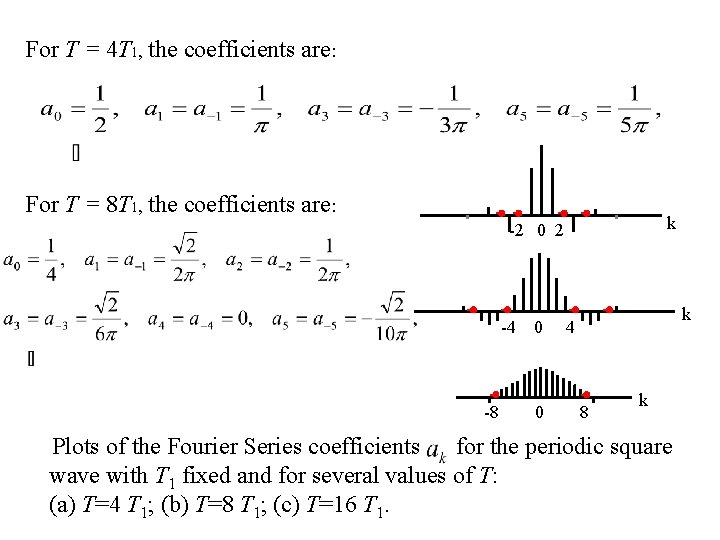
Example 3. 3 The periodic square wave is defined over one period as: x(t) … Represent it in Fourier series. … -T -T/2 -T 1 T/2 T t

For T = 4 T 1, the coefficients are: For T = 8 T 1, the coefficients are: k -2 0 2 -4 -8 0 0 k 4 8 k Plots of the Fourier Series coefficients for the periodic square wave with T 1 fixed and for several values of T: (a) T=4 T 1; (b) T=8 T 1; (c) T=16 T 1.

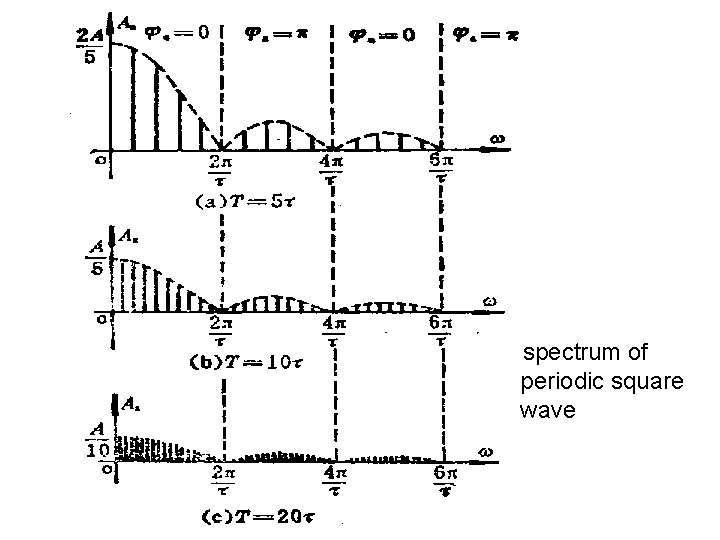
spectrum of periodic square wave

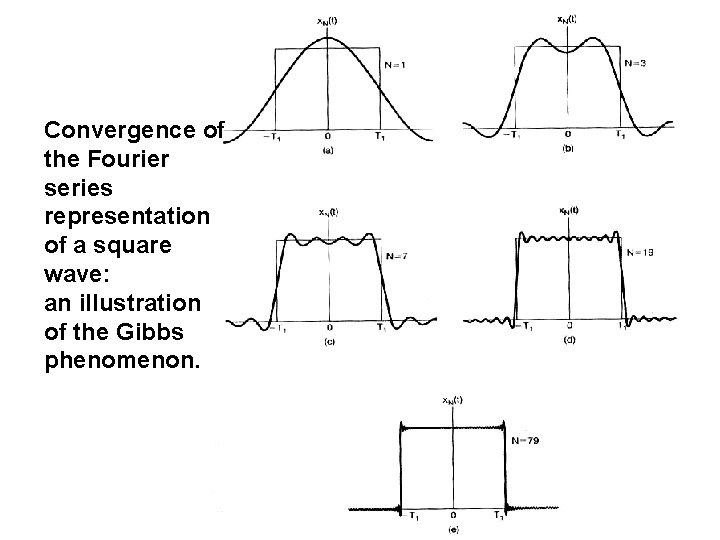
3. 3 CONVERGENCE OF THE FOURIER SERIES (傅立叶级数的存在性) An approximation of x(t) is There exist error between the original signal x(t) and the approximation x. N(t) and with the N increases, the error decreases. The Dirichlet conditions(狄里赫利条件) are as follows: üCondition 1: Over any period, x(t) must be absolutely integrable üCondition 2: In any finite interval of time, x(t) is of bounded variation; that is, there are no more than a finite number of maxima and minima during any single period of the signal. üCondition 3: In any finite interval of time, there are only a finite number of discontinuities. Furthermore, each of these discontinuities is finite.

v. For a periodic signal that has no discontinuities, the Fourier series representation converges and equals the original signal at every value of t. For a periodic signal with a finite number of discontinuities in each period, the Fourier series representation equals the signal everywhere except at the isolated points of discontinuity, at which the series converges to the average value of the signal on either side of the discontinuity. v. Gibbs phenomenon(吉布斯现象).

Convergence of the Fourier series representation of a square wave: an illustration of the Gibbs phenomenon.

3. 4 PROPERTIES FOURIER SERIES OF CONTINUOUS-TIME We generally use a shorthand notation to indicate the relationship between a periodic signal and its Fourier series coefficients, that is 3. 4. 1 Linearity If then

3. 4. 2 Time Shifting If then When a periodic signal is shifted in time, the magnitude spectrum remains unaltered. 3. 4. 3 Time Reversal If then Time reversal applied to a continuous-time signal results in a time reversal of the corresponding sequence of Fourier series coefficients. If x(t) is even : If x(t) is odd:

3. 4. 4 Time Scaling If then The Fourier coefficients for each of those components remain the same. However, the harmonic components change with the change in the fundamental frequency. 3. 4. 5 Multiplication If then hk is the convolution sum of the sequence representing the Fourier coefficients of x(t) and the sequence representing the Fourier coefficients of y(t).

3. 4. 6 Conjugation and Conjugate Symmetry (共轭对称) If then §if x(t) real, a 0 is real §if x(t) is real and even, then so are its Fourier series coefficients. §if x(t) is real and odd, then its Fourier series coefficients are purely imaginary and odd. 3. 4. 7 Parseval’s Relation for Continuous-Time Periodic Signals (帕色伐尔定理) Parseval’s relation states that the total average power in a periodic signal equals the sum of the average powers in all of its harmonic components.

Example 3. 4 Determine the Fourier series representation of g(t) which is shown in the following figure: g(t) 1/2 -2 -1 -1/2 1 2 t g(t)= x(t-1)– 1/2, where x(t) is the periodic square wave in Example 3. 3, and T=4 and T 1=1. time shifting property : the Fourier coefficients of x(t-1) is , where ak is the Fourier coefficients of x(t). -1/2 is the dc offset in g(t). ( supposing that the constant component in x(t) is a 0 , then the constant component in g(t) is a 0 – 1/2. ) linear property :

Example 3. 5 Consider the triangular wave signal x(t) which is shown in the x(t) following figure. 1 -2 2 t The derivative of x(t) is the signal g(t) in last example we just considered. Denoting the coefficients of g(t) by dk and those of x(t) by ek, then we have: ( differentiation property: ) Thus, For k = 0, e 0 can be determined by finding the area under one period of x(t) and dividing by the length of the period:

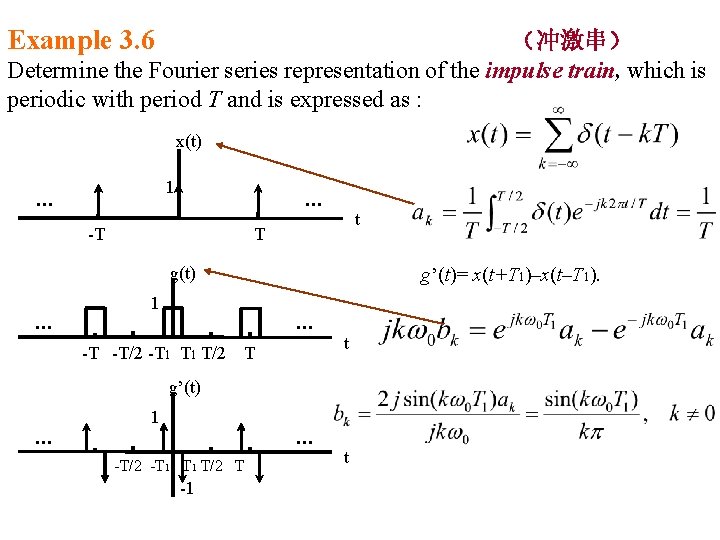
Example 3. 6 (冲激串) Determine the Fourier series representation of the impulse train, which is periodic with period T and is expressed as : x(t) 1 … … -T t T g(t) g’(t)= x(t+T 1)–x(t–T 1). 1 … … -T -T/2 -T 1 T/2 t T g’(t) 1 … … -T/2 -T 1 T/2 T -1 t

Example 3. 7 Giving the following facts about a signal x(t): 1. x(t) is a real signal; 2. x(t) is periodic with period T=4, and it has Fourier series coefficients ; 3. for ; 4. The signal with Fourier coefficients is odd; 5. . Determine the signal. or

3. 5 FOURIER SERIES REPRESENTATION OF DISCRETE-TIME PERIODIC SIGNALS 3. 5. 1 Linear Combination of Harmonically Related Complex Exponentials Given periodic x[n] with fundamental period N , its Fourier series has the form: Since

This means that discrete-time complex exponentials which differ in frequency by a multiple of 2π are identical. Consequently, there are only N distinct signals in the set The summation need only include terms over a range of N successive values of k. We use to indicate this. Then, finite series

3. 5. 2 Determination of the Fourier Series Representation of a Periodic Signal Multiplying both sides of the discrete-time Fourier series equation by and summing over N terms, we obtain Interchanging the order of summation on the right-hand side, we have

the Fourier series coefficients are determined by equation: synthesis equation: analysis equation: periodic Discreteness ↔ Periodicity
![Example 3 8 Consider the signal xn sin 32π5n draw the graph of Example 3. 8 Consider the signal x[n] = sin 3(2π/5)n, draw the graph of](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-30.jpg)
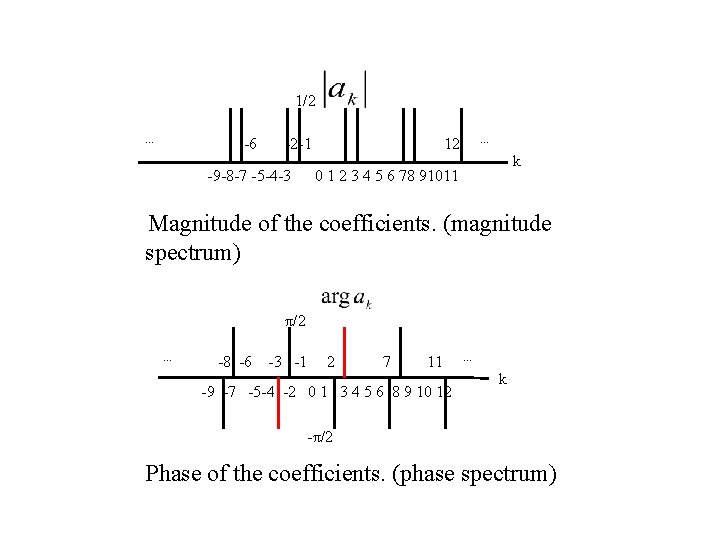
Example 3. 8 Consider the signal x[n] = sin 3(2π/5)n, draw the graph of coefficients. This signal is periodic with period N = 5. 1/2 j … … -8 -7 -3 2 -2 7 3 12 8 k -1/2 j Fourier coefficients for x[n]=sin 3(2π/5)n.

1/2 … -6 -2 -1 -9 -8 -7 -5 -4 -3 … 12 k 0 1 2 3 4 5 6 78 91011 Magnitude of the coefficients. (magnitude spectrum) π/2 … -8 -6 -3 -1 2 7 11 -9 -7 -5 -4 -2 0 1 3 4 5 6 8 9 10 12 … k -π/2 Phase of the coefficients. (phase spectrum)

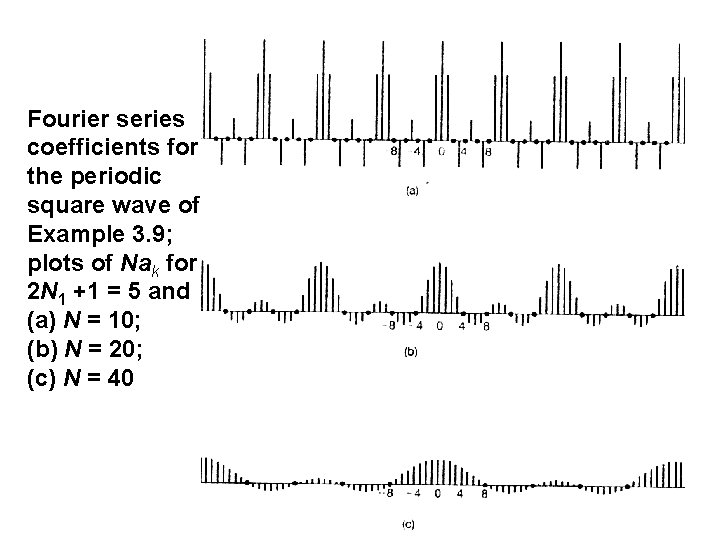
Example 3. 9 Consider the discrete-time periodic square wave: 1 … … –N –N 1 0 N 1 N n

ØThere are no convergence issues with the discrete-time Fourier series in general, because any discrete-time periodic sequence x[n] is completely specified by a finite number N of parameters.

Fourier series coefficients for the periodic square wave of Example 3. 9; plots of Nak for 2 N 1 +1 = 5 and (a) N = 10; (b) N = 20; (c) N = 40

3. 6 PROPERTIES FOURIER SERIES OF DISCRETE-TIME 3. 6. 1 Multiplication If and then 3. 6. 2 First Difference If then periodic convolution

3. 6. 3 Parseval’s Relation for Discrete-Time Periodic Signals is the average power in the kth harmonic component of x[n]. Parseval’s relation states that the average power in a periodic signal equals the sum of the average powers in all of its harmonic components. Different from the continuous time case, in discrete time, there are only N distinct harmonic components. Example 3. 10 Find the Fourier series coefficients figure: of the sequence x[n] shown in the x[n] 2 1 … … -5 0 5 n
![1 5 x 1n 0 5 x 2n 1 5 n 1 … -5 x 1[n] … 0 5 x 2[n] 1 … -5 n](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-37.jpg)
1 … -5 x 1[n] … 0 5 x 2[n] 1 … -5 n … 0 n 5 Representing x[n] as a sum of the square wave x 1[n] and the dc sequence x 2[n]
![Example 3 11 Giving the following facts about a sequence xn 1 xn is Example 3. 11 Giving the following facts about a sequence x[n]: 1. x[n] is](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-38.jpg)
Example 3. 11 Giving the following facts about a sequence x[n]: 1. x[n] is periodic with period N = 6. 2. 3. 4. x[n] has the minimum power period among the set of signals satisfying the preceding three conditions. Determine the sequence x[n].

3. 7 FOURIER SERIES AND LTI SYSTEMS system function(系统函数) If Re{s} = 0, s = jω. If | z| = 1, . frequency response (频率响应)

In continuous time, let x(t) be a periodic signal with Fourier series representation given by Then, the output is That is, the effect of the LTI system is to modify individually each of the Fourier coefficients of the input through multiplication by the value of the frequency response at the corresponding frequency.
![In discrete time let xn be a periodic signal with Fourier series representation given In discrete time, let x[n] be a periodic signal with Fourier series representation given](https://slidetodoc.com/presentation_image_h2/4819cb264631d4e18f4b21c798561c58/image-41.jpg)
In discrete time, let x[n] be a periodic signal with Fourier series representation given by Then, the output is Thus, y[n] is also periodic with the same period as x[n], and the kth Fourier coefficient of y[n] is the product of the kth Fourier coefficient of the input and the value of the frequency response of the LTI system at the corresponding frequency.

Example 3. 12 Input periodic signal system with impulse response as in example 3. 1 to an LTI Determine the Fourier series coefficients bk of the output y(t). First compute the frequency response: Since
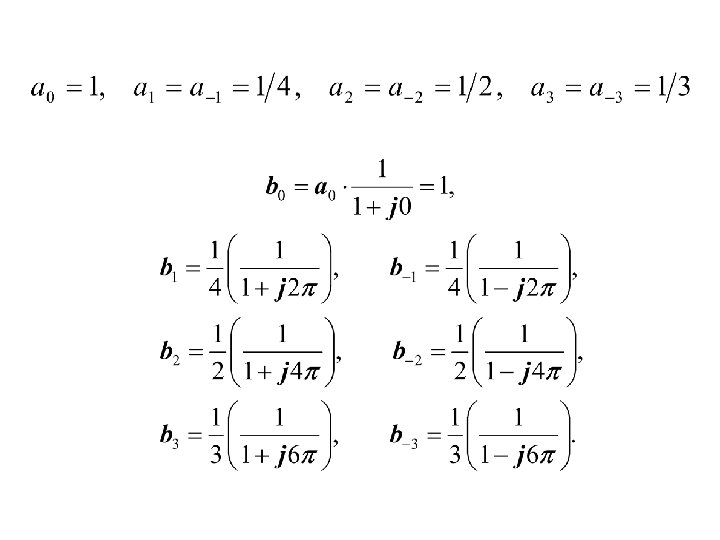

Example 3. 13 Consider an LTI system with sample response and with the input Determine the output y[n]. First compute the frequency response: Since x[n] can be written in Fourier series form as

So, the Fourier series for the output: If we write Then we have

3. 8 SUMMARY 1. Eigenfunction property of complex exponentials; 2. Fourier series representations for both continuous-time and discretetime periodic signals ― i. e. , weighted sum of harmonically related complex exponentials that share a common period; 3. Different characteristics of signals reflected in their Fourier series coefficients (properties of Fourier series); 4. An important conclusion: if a periodic signal is applied to an LTI system, then the output will be periodic with the same period, and each of the Fourier coefficients of the output is the corresponding Fourier coefficient of the input multiplied by a complex number whose value is a function of the frequency corresponding to that Fourier coefficient. 5. The concepts of system function and frequency response.