CHAPTER 3 Forced Vibration of Single Degree of

CHAPTER 3 Forced Vibration of Single Degree of Freedom System

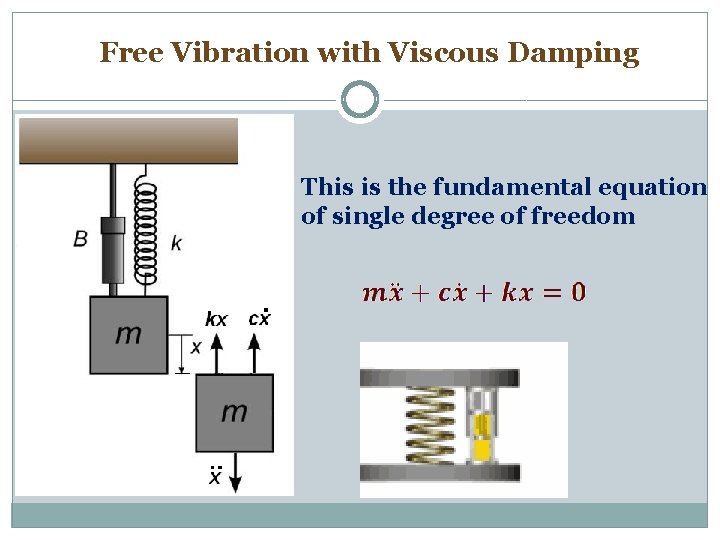
Free Vibration with Viscous Damping This is the fundamental equation of single degree of freedom

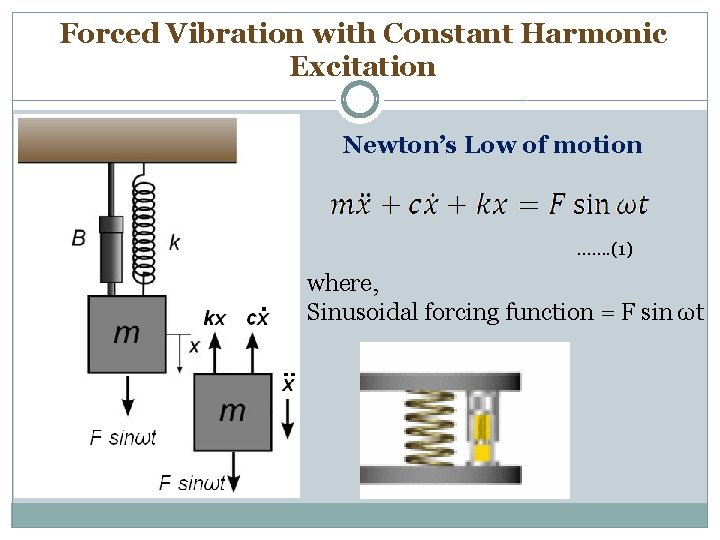
Forced Vibration with Constant Harmonic Excitation Newton’s Low of motion ……. (1) where, Sinusoidal forcing function = F sin ωt

Forced Vibration with Constant Harmonic Excitation …. (1) This is the non linear, non homogeneous, second order differential equation The Complete Solution of the Equation is = Complementary function + Particular Integral

Complementary function can find by taking RHS zero The roots of the second order differential equation are as follow. For Under damped Vibration System ( ζ < 1 ) …. (2) Where, xc is the Complimentary Function

For finding Particular Integral Particular Solution is a steady state harmonic oscillation and the displacement vector lags the force by some angle …. …(3) Where, X is the amplitude of vibration Differentiating equation (3) twice Substituting the vale of above equation in equation (1)

Equation (1) become

While constructing vector diagram following points must consider 1. The force vector F is acting at an angle ωt from the reference axis 2. The displacement lags the impress force by an angle �� 3. The spring force is always opposite in direction to the displacement 4. The damping force lags the displacement by 90°. it follows that the damping force is always opposite in the direction to the velocity. 5. The inertia force is in phase with the displacement. Since the acceleration is out of phase with the displacement, therefore the inertia force is always opposite in direction to the acceleration.

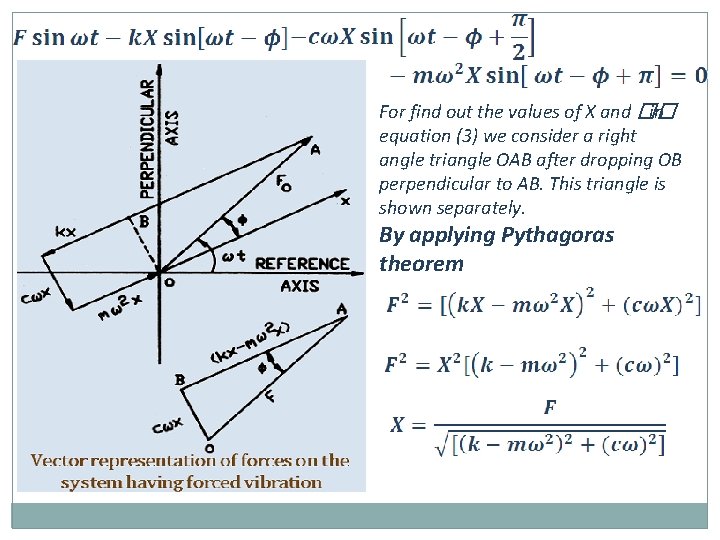
For find out the values of X and �� in equation (3) we consider a right angle triangle OAB after dropping OB perpendicular to AB. This triangle is shown separately. By applying Pythagoras theorem

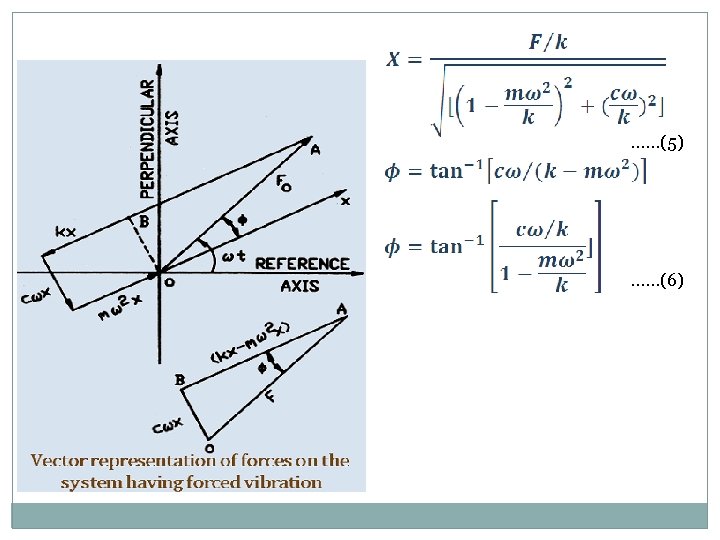
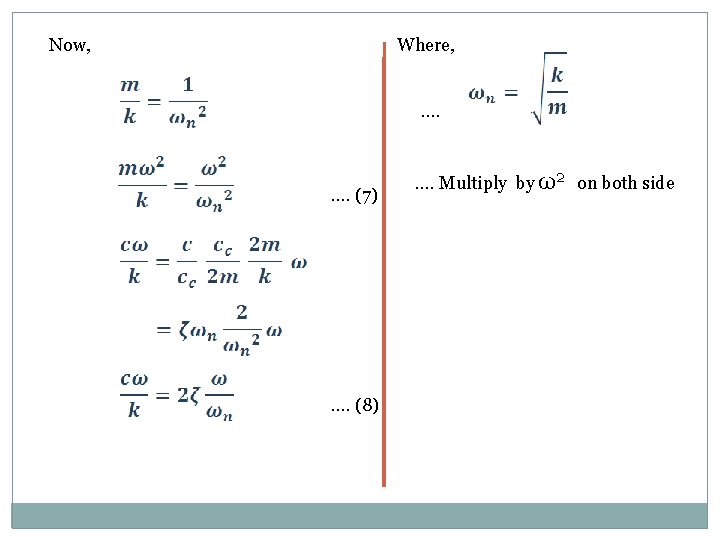
Now, Where, …. (7) …. (8) …. Multiply by ω2 on both side

Zero frequency deflection of the spring mass system under the steady force F …. (9) Substituting the expression (7), (8) and (9) in equation (5) …. (10) and …. (11) Particular Solution of the equation (3) may be written as …. (12)

The Complete Solution of the Equation is x = Complementary function + Particular Integral x = xc + xp This is the complete solution to an under damp system subjected to sinusoidal excitation

Thank you …. .