Chapter 3 Force and Stress In geology the

Chapter 3 Force and Stress

In geology, the force and stress have very specific meaning. • Force (F): the mass times acceleration (ma) (Newton’s second law); F=ma. • Stress (σ): Force per unit area (F/A); σ = F/A Stress can be considered as the intensity of force. σ = (ma/A) = (kg. m-1. s-2), which is called Pascal (Pa).

Stress Megapascal (MPa) = 106 Pa and Gigapascal (GPa) = 109 Pa In geology we used (bar) = 105 Pa 1 kbar = 1000 bar = 108 Pa = 100 MPa = 0. 1 GPa

• Tensors: The forces within the earth act over surfaces or through volumes of material, and they generate stresses which are three-dimensional entities.

• Mechanics: is the branch of science which concerned with the action of forces on bodies and their effect. • In nature we can recognize four basic forces: 1. Gravitational force 2. Electromagnetic force 3. Nuclear or strong force 4. Weak force

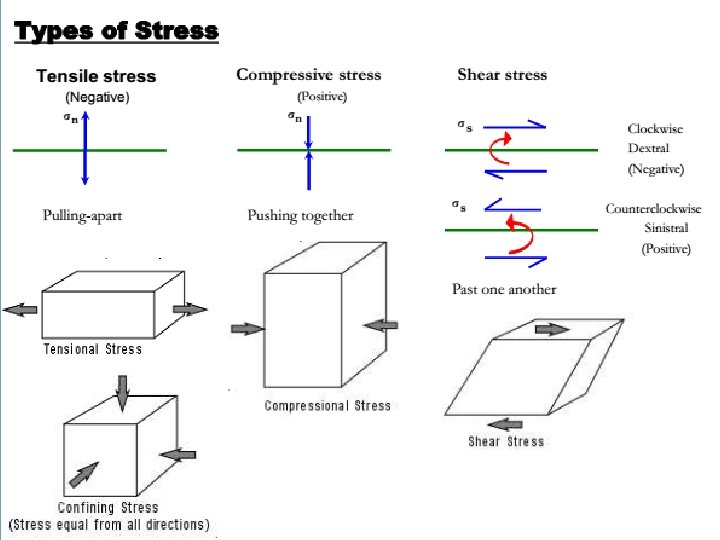
• Body forces: are forces that result from action of a field at every point within the body. • Surface forces: are forces that act on a specific surface area in a body.

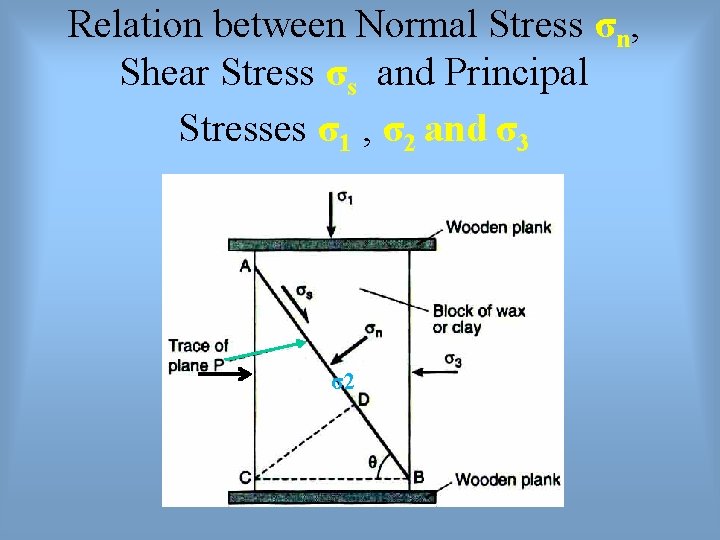
Normal Stress (σn) and Shear (σs) or τ

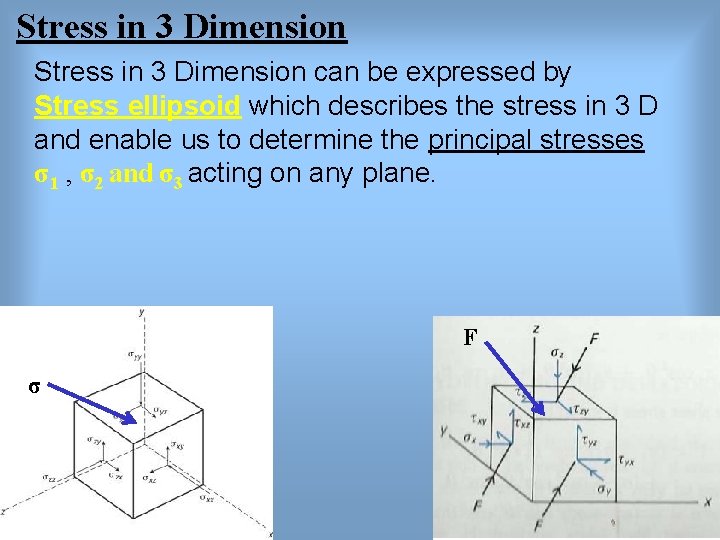
Stress in 3 Dimension can be expressed by Stress ellipsoid which describes the stress in 3 D and enable us to determine the principal stresses σ1 , σ2 and σ3 acting on any plane. F σ

Principal Stresses

σ3 σ1 Stress ellipse: stress in 2 D

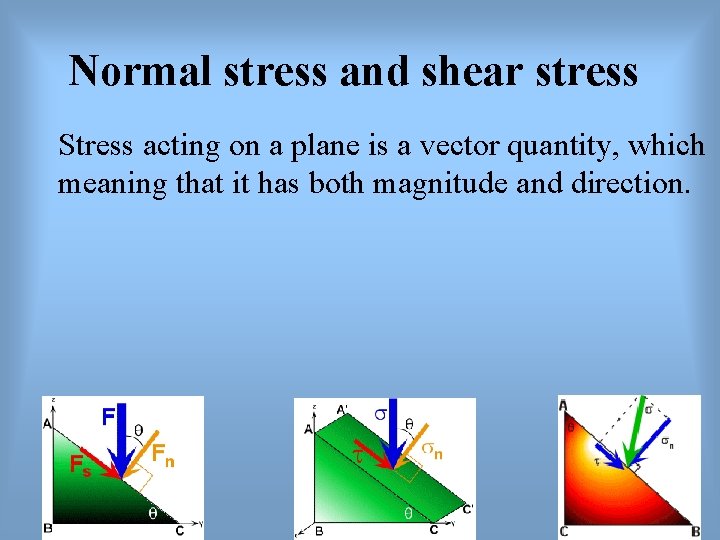
Normal stress and shear stress Stress acting on a plane is a vector quantity, which meaning that it has both magnitude and direction.

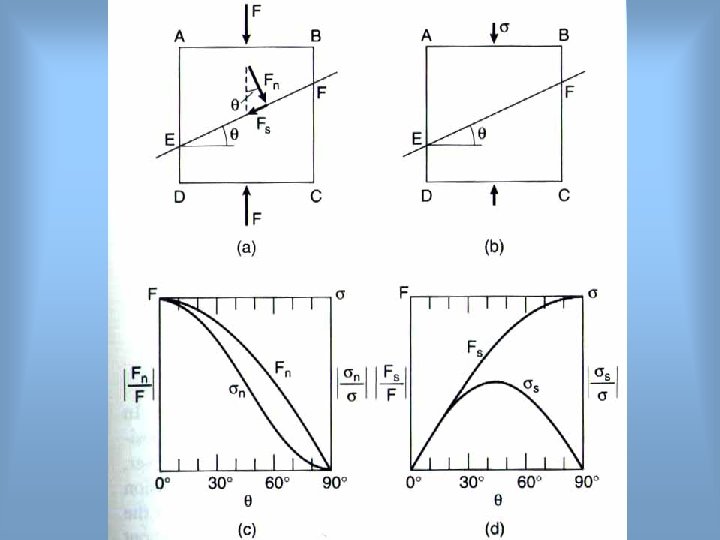
Fn = F * cosθ = σ EF cos 2θ Fs = = F * sinθ =½σ EF (sin 2θ) Thus the stresses are: σn = Fn/EF = σ cos 2θ σs = Fs/EF = ½σ (sin 2θ)

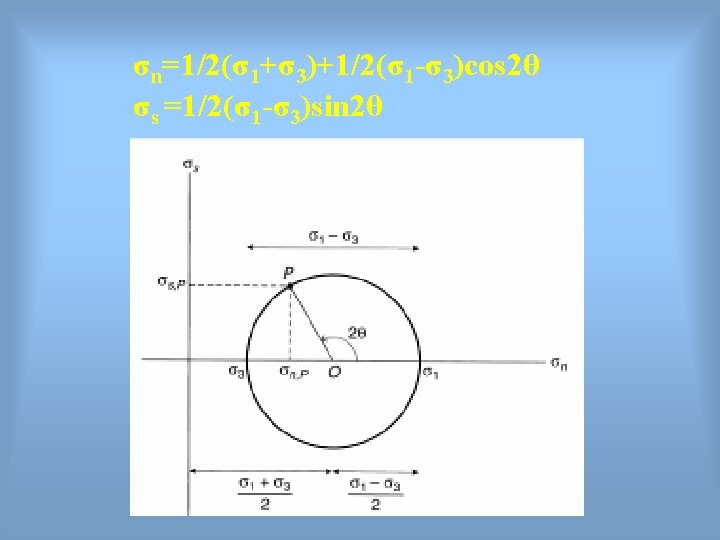
Relation between Normal Stress σn, Shear Stress σs and Principal Stresses σ1 , σ2 and σ3 σ2

Applications to Geological structures

σn=1/2(σ1+σ3)+1/2(σ1 -σ3)cos 2θ σs =1/2(σ1 -σ3)sin 2θ

Application on Mohr Circle • Problem 1 Given the principle stresses of σ1 =100 MPa (vertical) and σ3 = 20 MPa (horizontal), determine the normal stress σn and shear stress σs on a fault plane that strikes parallels to σ2 and dips 32° with σ3 .

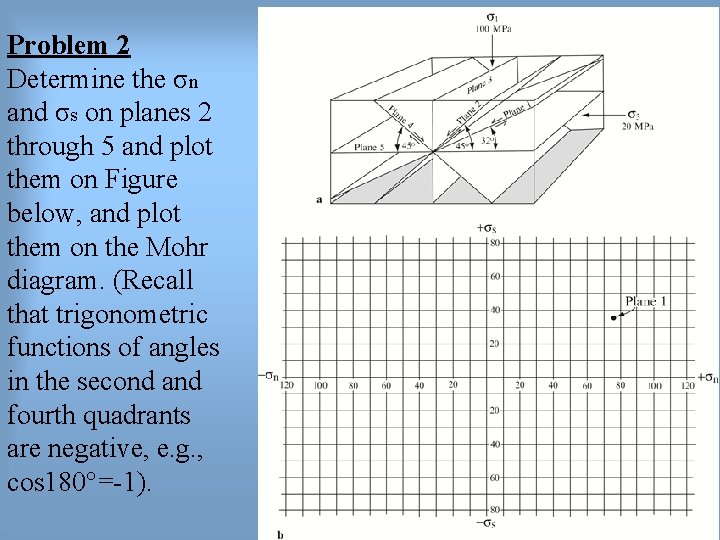
Problem 2 Determine the σn and σs on planes 2 through 5 and plot them on Figure below, and plot them on the Mohr diagram. (Recall that trigonometric functions of angles in the second and fourth quadrants are negative, e. g. , cos 180°=-1).

PROBLEM 3 • If σ1 is vertical and equal to 50 MPa and σ3 is horizontal, E-W, and equal to 22 MPa, using a Mohr circle construction to determine the normal and shear stresses on a fault striking N -S and dipping 60 o E.

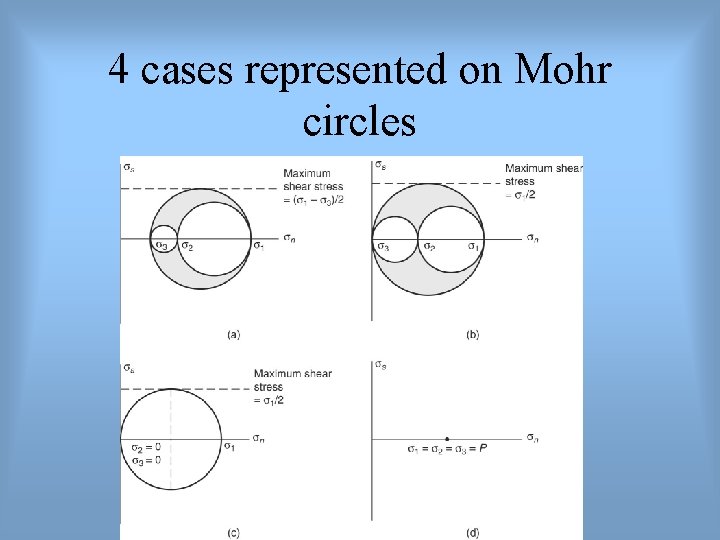
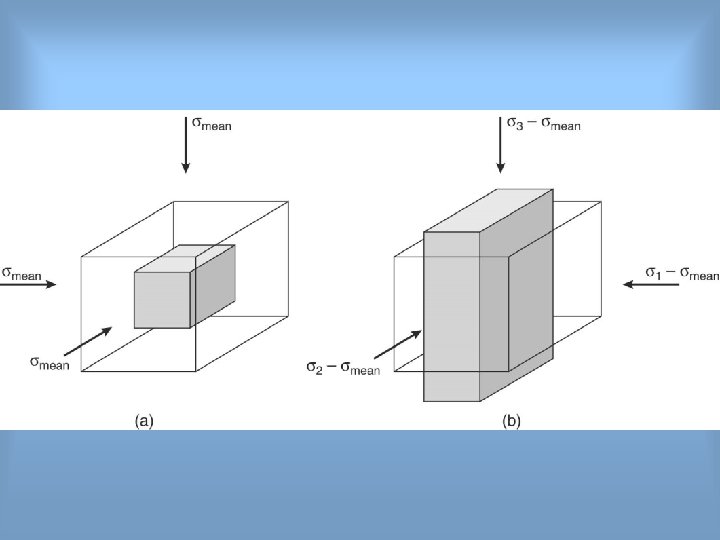
Stress states σ1 σ2 σ3 The following relationships between the principal stresses define common stress states: General triaxial stress: σ1 > σ2 > σ3 0 Biaxial (plane) stress: σ1 > 0 > σ3, one axis=0 Uniaxial tension : σ1 = σ2 = 0; σ3 < 0 Uniaxial compression: σ2 = σ3 = 0; σ1> 0 Hydrostatic stress (pressure): σ1 = σ2 = σ3

4 cases represented on Mohr circles

Isotropic and Anisotropic stresses • Isotropic stress: a. hydrostatic pressure b. lithostatic pressure They form change in volume • σ= ρ*g*h (Pa) =2700*9. 8*1500=39690000=396. 9 Bar • Anisotropic (Deviatoric) stress : It forms changes in the shape of a body (strain). It is due to the tectonic stresses

Homogenous and Heterogeneous stress field: • Homogenous: the stress field is the same in magnitude and orientation at every point throughout the body. • It is heterogeneous if it is not the same. Here, you must differentiate between homogenous and isotropic. Source of inhomogenity in the crust are: 1. Fracture in rocks 2. Contrast in viscosity 3. The complex interplay of more than one stress field.

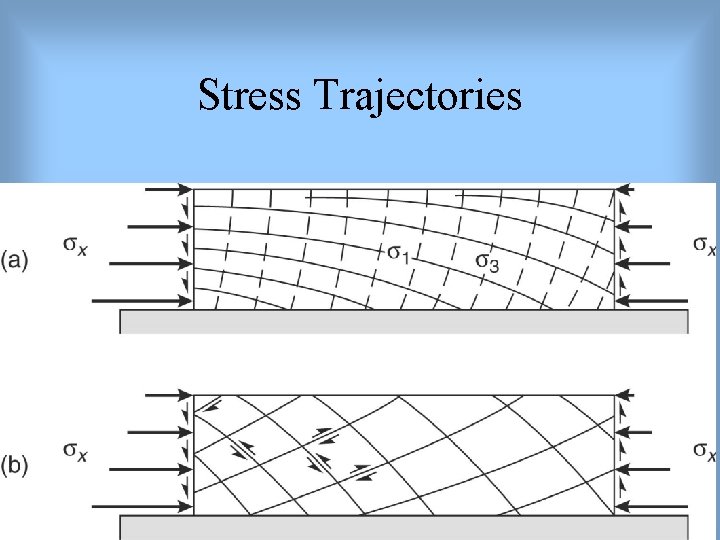
Stress Trajectories

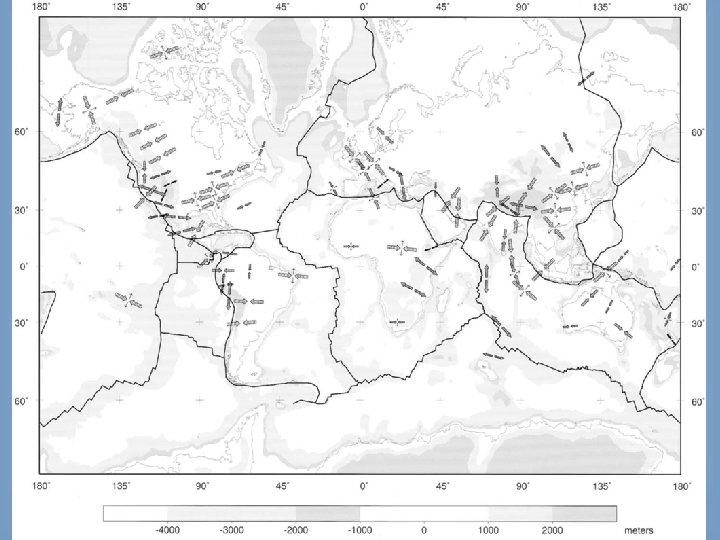
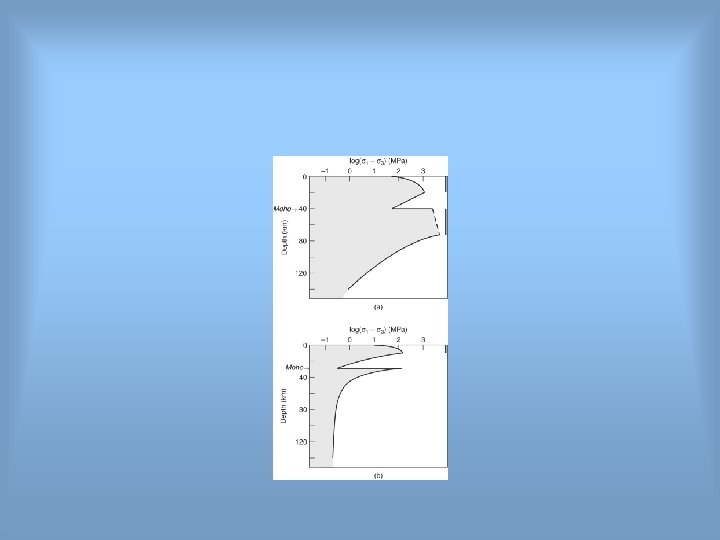
Methods of stress measurement 1. Present-day stress: by analysis of fault planes and fractures • Bore-hole breakouts • Hydrofracturing • Strain release (In-situ stress measurements) • Analysis of faults and fractures • Fault-plane solutions (Earthquake focal mechanisms) 2. Paleostress: through determine stresses on fault plane by measuring attitudes of fault and slickenlines pitches. 3. Stress in the earth: We can divided the global stress field into "stress provinces", which generally correspond to geologic provinces (Fig. 3. 11).

• The main present-day driving forces (stress field) of plate tectonic include: 1. Pull of the down-going slab in subduction zones (Slab pull) 2. Push at ocean ridges (Ridge Push) 3. Continent-continent collision