CHAPTER 3 EXPONENTIAL LOGISTIC AND LOGARITHMIC FUNCTIONS Overview




































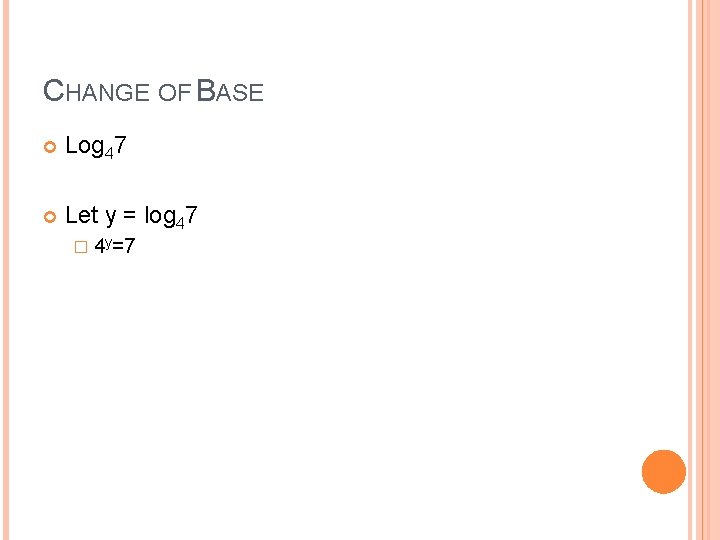







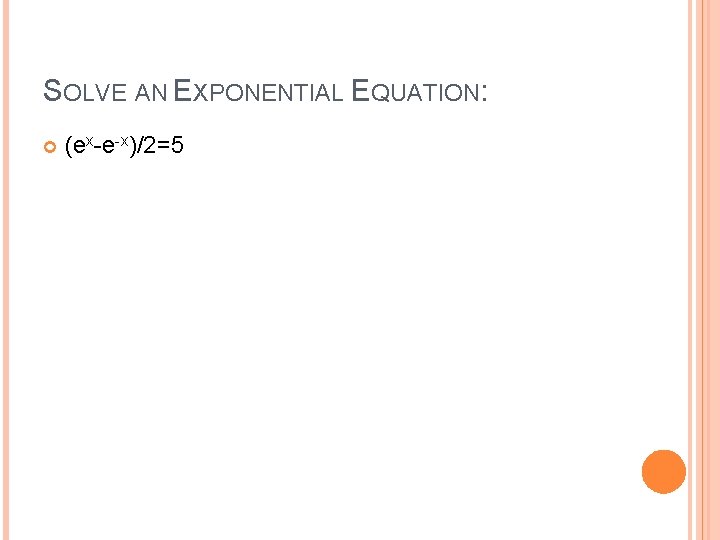
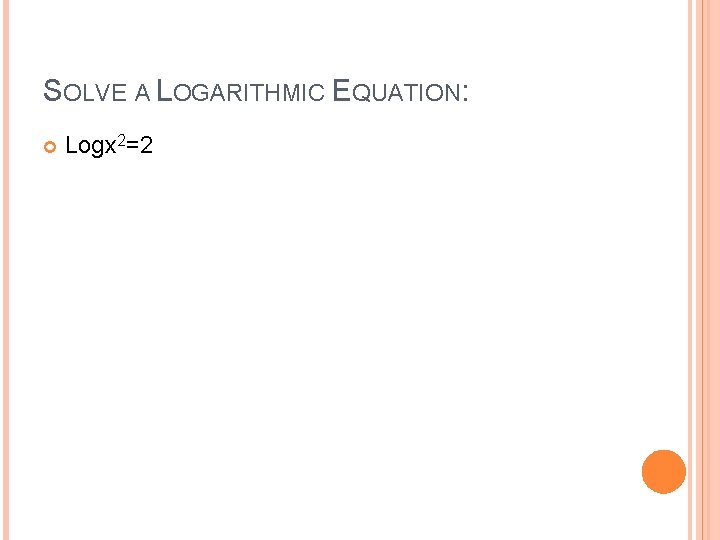
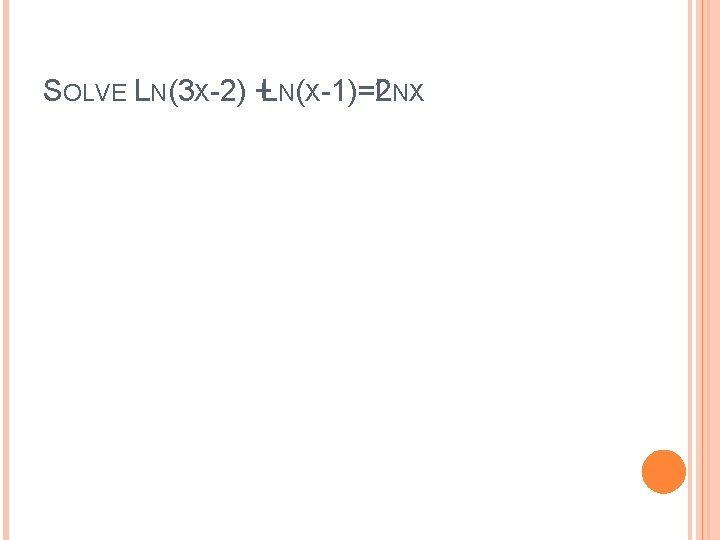






- Slides: 61

CHAPTER 3 –EXPONENTIAL, LOGISTIC, AND LOGARITHMIC FUNCTIONS Overview: interrelationships between exponential, logistic, and logarithmic functions. Polynomial, rational, and power functions with rational exponents are algebraic functions. In this chapter, we will explore transcendental functions.

TRANSCENDENTAL FUNCTIONS: Exponential functions- model growth and decay over time � Ex: unrestricted population growth and the decay of radioactive substances Logistic functions- model restricted population growth, certain chemical reactions, and the spread of rumors and diseases. Logarithmic functions- are the basis of the Richter scale of earthquake intensity, the p. H acidity scale, and the decibel measurement of sound.

3. 1 EXPONENTIAL AND LOGISTIC FUNCTIONS Section 3. 1 #2 -10 e, 11 -14, 16 -36 e, 46 -54 e, 59 -64

THE FUNCTIONS F(X)=X 2 AND G(X)=2 X EACH INVOLVE A BASE RAISED TO A POWER, BUT THEIR ROLES ARE REVERSED: F(x)=x 2, the base is a variable x, the exponent is constant 2; F(x) is a ______ and __________. G(x)=2 x, the base is constant 2, the exponent is a variable x; G(x) is an exponential function. DEFINITION: � Let a and b be real number constants. An exponential function in x is a function that can be written in the form F(x)=a*bx, Where a is nonzero, b is positive, and b≠ 1. The constant a is the initial value of f (the value at x=0), and b is the base.

IDENTIFYING EXPONENTIAL FUNCTIONS: F(x)=4 x G(x)=7 x-5 H(x)=-3*3. 5 x K(x)=6*2 -x Q(x)=3*7�

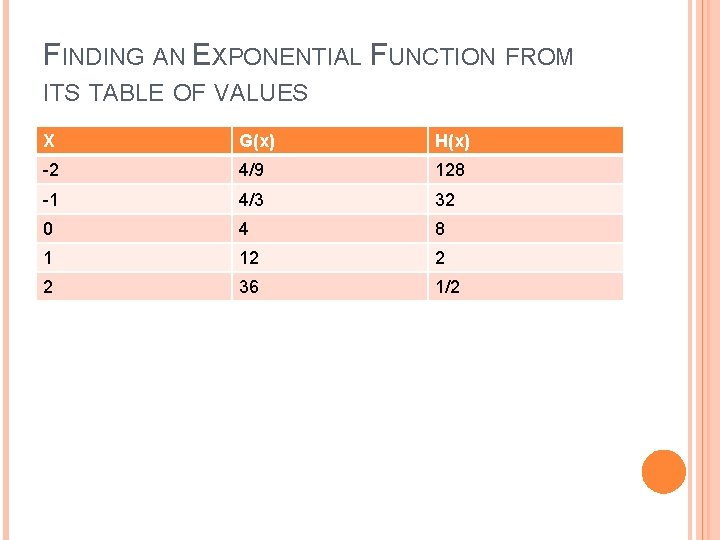
FINDING AN EXPONENTIAL FUNCTION FROM ITS TABLE OF VALUES X G(x) H(x) -2 4/9 128 -1 4/3 32 0 4 8 1 12 2 2 36 1/2

EXPONENTIAL GROWTH AND DECAY For any exponential function f(x)=a*bx and any real number x, F(x+1)=b*f(x) If a>0 and b>1, the function f is increasing and is an exponential growth function. The base b is its growth factor. If a>0 and b<1, f is decreasing and is an exponential decay function. The base b is its decay factor.

TRANSFORMING EXPONENTIAL FUNCTIONS F(X)=2 X G(x)=2 x-3 H(x)=2 -x K(x)=3*2 x

THE NATURAL BASE The functions f(x)=ex is one of the basic functions, exponential growth function. EXPONENTIAL FUNCTIONS AND THE BASE e � Any exponential function f(x)=a*bx can be written as F(x)=a*ekx For an appropriately chosen real number constant k. If a>0 and k>0, f(x)=a*ekx is an exponential growth function. If a>0 and k<0, f(x)=a*ekx is an _________ function.

TRANSFORMING EXPONENTIAL FUNCTIONS F(x)=ex � G(x)=e 2 x � H(x)=e-x � K(x)=3 ex

If a>0, how can you tell whether y=a*bx represents an increasing or decreasing function?

LOGISTIC FUNCTIONS AND THEIR GRAPHS Let a, b, c, and k be positive constants, with b<1. A logistic growth function in x is a function that can be written in the form � F(x)= � If c/(1+a*bx) or f(x)= c/(1+a*e-kx) Where the constant c is the “limit” to growth b>1 or k<0, these formulas are logistic _____ functions.

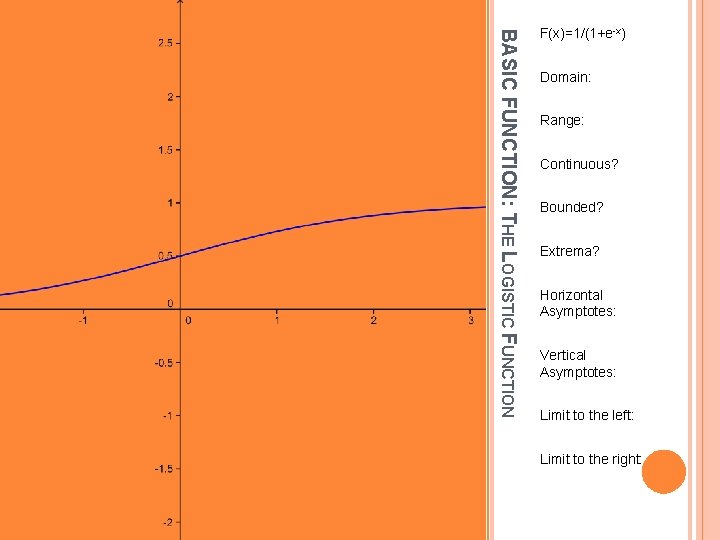
BASIC FUNCTION: THE LOGISTIC FUNCTION F(x)=1/(1+e-x) Domain: Range: Continuous? Bounded? Extrema? Horizontal Asymptotes: Vertical Asymptotes: Limit to the left: Limit to the right:

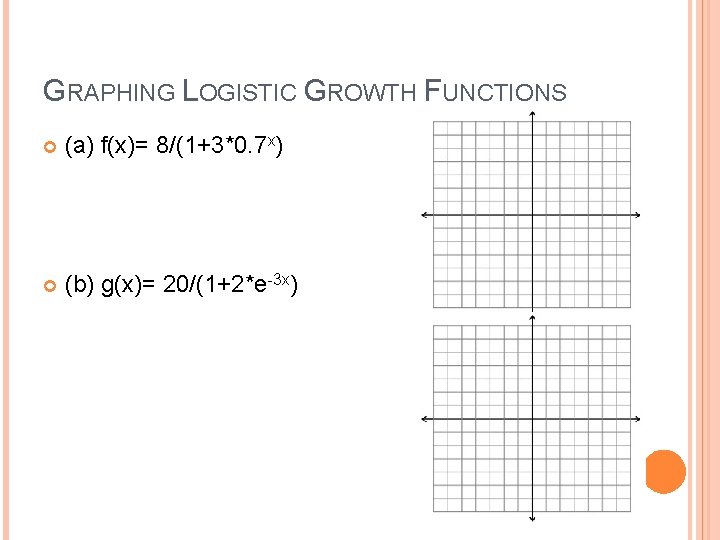
GRAPHING LOGISTIC GROWTH FUNCTIONS (a) f(x)= 8/(1+3*0. 7 x) (b) g(x)= 20/(1+2*e-3 x)

MODELING HOBOKEN’S POPULATION Year Population 1990 33, 397 2000 38, 577 Assuming the growth is exponential, when will the population of Hoboken surpass 1 million people? (HINT: Let P(t) be the population of Hoboken t years after 1990. Because P is exponential, P(t)=P 0*bt, where P 0 is the initial (1990) population of 33, 397)

DALLAS’S POPULATION Based on recent data, a logistic model for the population of Dallas, t years after 1900, is: � P(t)= 1, 301, 642/(1+21. 602 e-0. 05054 t) According to this model, when was the population 1 million?

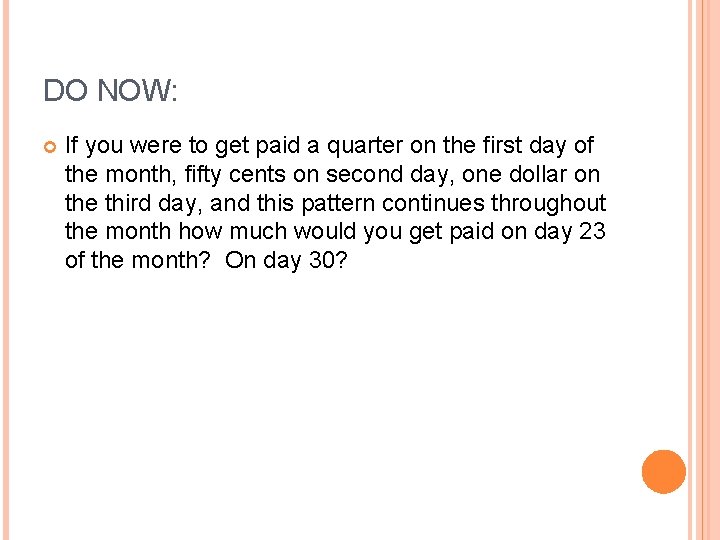
DO NOW: If you were to get paid a quarter on the first day of the month, fifty cents on second day, one dollar on the third day, and this pattern continues throughout the month how much would you get paid on day 23 of the month? On day 30?

3. 2 – EXPONENTIAL AND LOGISTIC MODELING HW: Pg 296 #7 -20 e For extra credit: #28

IF A CULTURE OF 100 BACTERIA IS PUT INTO A PETRI DISH AND THE CULTURE DOUBLES EVERY HOUR, HOW LONG WILL IT TAKE TO REACH 400, 000? IS THERE A LIMIT TO GROWTH? Time (in hours) 0 1 2 3 4 Bacteria

EXPONENTIAL POPULATION MODEL If a population P is changing at a constant percentage rate r each year, then P(t)=P 0(1+r)t Where P 0 is the initial population, r is expressed as a decimal, and t is time in years. If r>0, then P(t) is an exponential growth function, and its growth factor is the base of the exponential function, 1+r.

FINDING GROWTH AND DECAY RATES Tell whether the population model is an exponential growth function or exponential decay function, and find the constant percentage rate of growth or decay. (a) San Jose: P(t)=782, 248*1. 0136 t (b) Detroit: P(t)=1, 203, 368*0. 9858 t

DETERMINE THE EXPONENTIAL FUNCTION THAT SATISFIES THE GIVEN CONDITIONS: Initial value=5, increasing at a rate of 17% per year Initial value=16, decreasing at a rate of 50% per month Initial population= 28900, decreasing at a rate of 2. 6% per year Initial mass = 0. 6 g, doubling every 3 days Initial mass= 592 g, halving once every 6 years

MODELING TWO STATES’ POPULATIONS USING LOGISTIC REGRESSION The populations (in millions) of Florida and Pennsylvania is represented with models: � F(t)=28. 021/(1+9018. 63 -0. 047015 t) � P(t)=12. 579/(1+29. 0003 e-0. 034315 t) What are the limits?

MODELING A RUMOR Forks High School has 1200 students. Eric, Jessica, Mike, and Angela start a rumor that Edward and Bella are dating, which spreads logistically so that S(t)=1200/(1+39*e-0. 9 t) models the number of students who have heard the rumor by the end of t days, where t=0 is the day the rumor begins to spread. � (a) How many students have the rumor by the end of Day 0? � (b) How long does it take for 1000 students to hear the rumor?

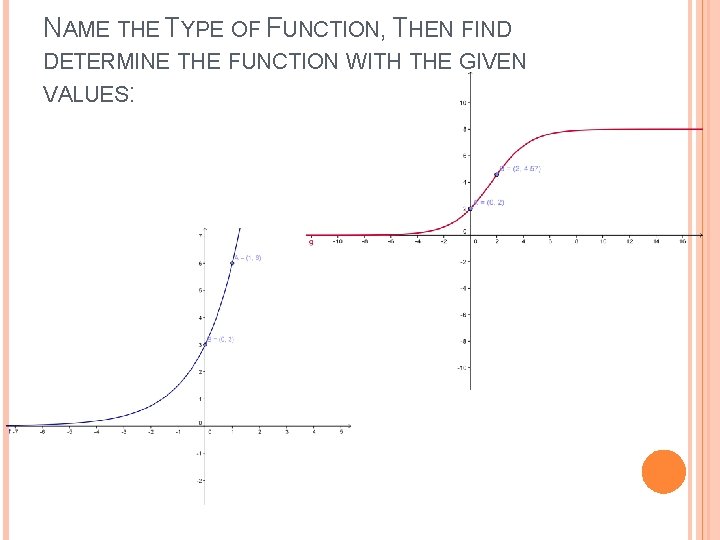
NAME THE TYPE OF FUNCTION, THEN FIND DETERMINE THE FUNCTION WITH THE GIVEN VALUES:

3. 3 – LOGARITHMIC FUNCTIONS AND THEIR GRAPHS HW: Pg. 308 #1 -18 e

CHANGING BETWEEN LOGARITHMIC AND EXPONENTIAL FORM If x>0 and 0 < b≠ 0, then Y=logb(x) IFF by=x (a) log 28=3 because 23=8 (b) log 3√ 3=1/2 because 31/2=√ 3 (c) log 51/25 = -2 because 3 -2=1/5 -2=1/25 (d) log 41=___ because 4__ = 1 (e) log 77=___ because 7__ = 7

BASIC PROPERTIES OF LOGARITHMS For 0<b≠ 1, x>0, and any real number y. logb 1=___ because b logbby=___ because b = by Blogbx=___ because logbx=

EVALUATING LOGARITHMIC AND EXPONENTIAL EXPRESSIONS LOGBBY=Y (a) log 28= (b) log 3√ 3= (c) 6 log 611=

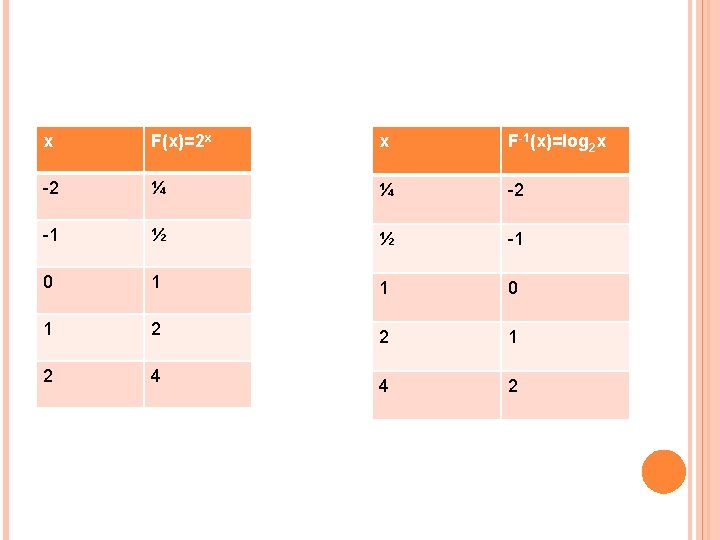
x F(x)=2 x x F-1(x)=log 2 x -2 ¼ ¼ -2 -1 ½ ½ -1 0 1 2 2 1 2 4 4 2

COMMON LOGARITHMS-BASE 10 Logarithms with base 10 are called common logarithms. The common logarithmic function log 10 x=log x, which is the inverse of the exponential function f(x)=10 x So y=logx IFF 10 y=x

BASIC PROPERTIES OF COMMON LOGARITHMS Let x and y be real numbers with x>0. � Log 1=0 because 100=1 � Log 10=1 because 101=10 � Log 10 y=y because 10 y=10 y � 10 Logx=x because log x = log x

EVALUATE LOGARITHMIC AND EXPONENTIAL EXPRESSIONS-BASE 10 Log 100= Log 5√ 10= Log 1/1000= 10 log 6= HW: Pg. 308 # 33 -52 e

EVALUATING COMMON LOGARITHMS WITH A CALCULATOR (a) log 36. 5 = (b) log. 46 = Solving Simple Logarithmic Equations Log x = 4 Log 2 x= 5

NATURAL LOGARITHMS – BASE E We often use the special abbreviation “ln” to denote a natural logarithm. � Logex=lnx �Y = ln x IFF _______

BASIC PROPERTIES OF NATURAL LOGARITHMS Let x and y be real numbers with x>0 � Ln 1 = 0 because ______ � Ln e = __ because _______ � Ln ey = ___ because ____ � elnx = x because ln x = ln x

EVALUATE LOGARITHMS: Ln√e = Ln e 5 = eln 4 = Ln 23. 5 = Ln 0. 5 =

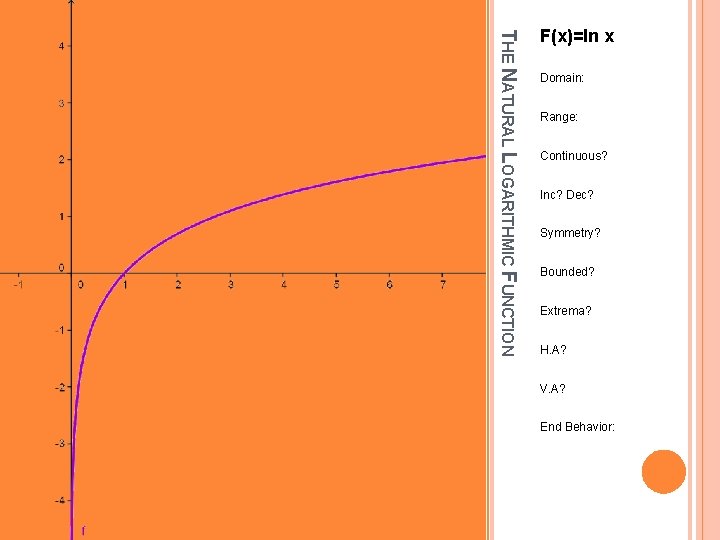
THE NATURAL LOGARITHMIC FUNCTION F(x)=ln x Domain: Range: Continuous? Inc? Dec? Symmetry? Bounded? Extrema? H. A? V. A? End Behavior:

TRANSFORMING LOGARITHMIC GRAPHS Y = LN X OR Y = LOG X G(x)= ln (x+4) G(x)= ln (5 -x) H(x)= 6 log x H(x)= 8 + log x

3. 4 – PROPERTIES OF LOGARITHMIC FUNCTIONS Pg. 317 #18 -36 e

PROPERTIES OF LOGARITHMS Let b, R, and S be positive real numbers with b≠ 1, any real number. Product rule: logb(RS) = logb. R + logb. S Quotient rule: logb(R/S) = logb. R – logb. S Power rule: logb. Rc = c logb. R

EXPANDING THE LOGARITHM OF A PRODUCT Log (8 xy 4) = Ln √(x 2+5)/x

CONDENSING A LOGARITHMIC EXPRESSION Lnx 4 – 3 lnxy 6 lnx – 4 ln 3 x
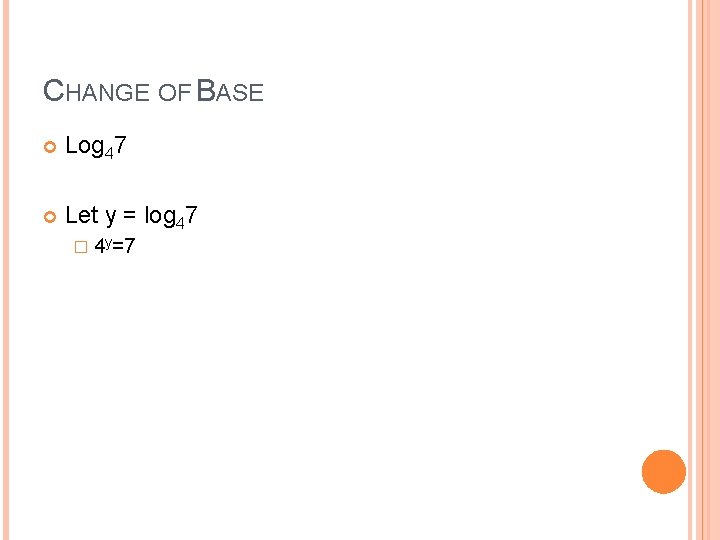
CHANGE OF BASE Log 47 Let y = log 47 � 4 y=7

CHANGE-OF-BASE FORMULA FOR LOGARITHMS For positive real numbers a, b, and x with a≠ 1 and b≠ 1. Logbx = logax/logab Logbx = logx/logb OR Logbx = lnx/lnb

EVALUATE LOGARITHMS BY CHANGING THE BASE Log 417= Log 210= Log 1/22=

GRAPHS OF LOGARITHMIC FUNCTIONS WITH BASE B We can rewrite any logarithmic function g(x)=Logbx as: � G(x)=lnx/lnb=(1/lnb)lnx So every logarithmic function is a constant multiple of the natural log function f(x)=lnx If the base is b>1, the graph of g(x)=Logbx is vertical stretch or shrink of the graph of f(x)=lnx by the factor 1/lnb. If 0<b<1, a reflection across the x-axis is required as well

DESCRIBE HOW TO TRANSFORM THE GRAPH F(X)=LNX INTO: (a) G(x)=Log 5 x (b) H(x)=Log 1/4 x

3. 5 –EQUATION SOLVING AND MODELING HW: Pg. 331 #1 -30 e

SOLVING EXPONENTIAL EQUATIONS One-To-One Properties � For any exponential function f(x)=bx, If bu =bv , then u=v. For any logarithmic function f(x)=logbx If logbu=logbv, then u=v

SOLVING AN EXPONENTIAL EQUATION ALGEBRAICALLY Solve 20(1/2)x/3 = 5
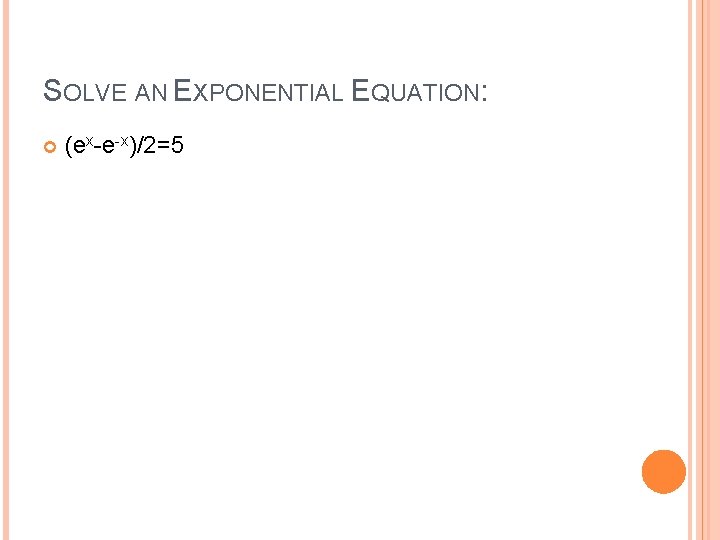
SOLVE AN EXPONENTIAL EQUATION: (ex-e-x)/2=5
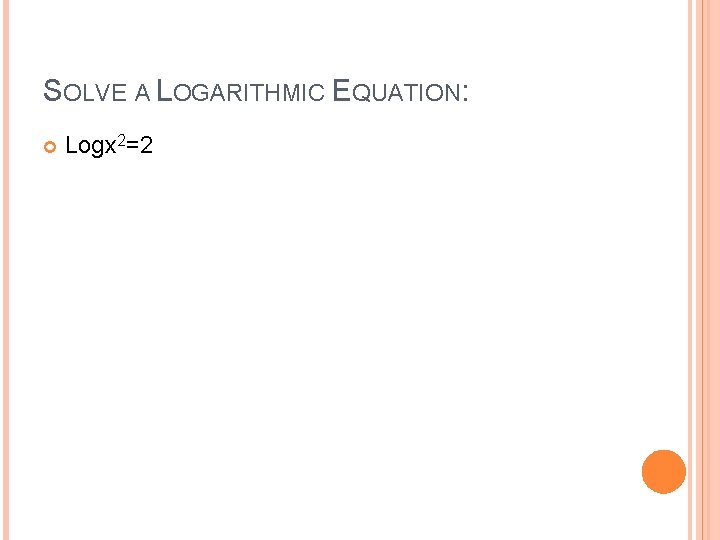
SOLVE A LOGARITHMIC EQUATION: Logx 2=2
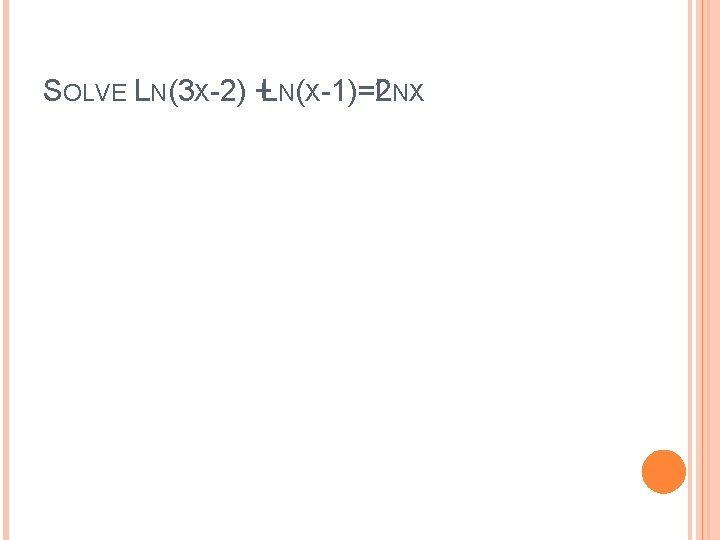
SOLVE LN(3 X-2) +LN(X-1)=2 LNX

3. 6 – MATHEMATICS OF FINANCE

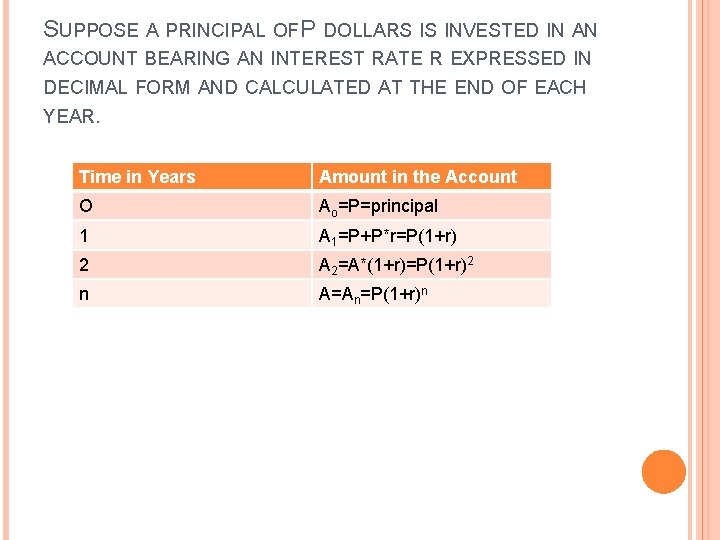
SUPPOSE A PRINCIPAL OF P DOLLARS IS INVESTED IN AN ACCOUNT BEARING AN INTEREST RATE R EXPRESSED IN DECIMAL FORM AND CALCULATED AT THE END OF EACH YEAR. Time in Years Amount in the Account O Ao=P=principal 1 A 1=P+P*r=P(1+r) 2 A 2=A*(1+r)=P(1+r)2 n A=An=P(1+r)n

SUPPOSE WEEHAWKEN TOWNSHIP INVESTS $500 AT 7% INTEREST COMPOUNDED ANNUALLY. FIND THE VALUE OF WEEHAWKEN’S INVESTMENT 10 YEARS LATER. Let P=_______, r=____, and n=____

INTEREST COMPOUNDED K TIMES PER YEAR Suppose a principal P is invested at an annual interest rate r compounded k times a year for t years. Then r/k is the interest rate per compounding period and kt is the number of compounding periods. The amount A in the account after t years is • A=P(1+r/k)kt

SUPPOSE JENNIFER INVESTS $500 AT 9% ANNUAL INTEREST COMPOUNDED MONTHLY (COMPOUNDED 12 TIMES A YEAR). FIND THE VALUE OF HER INVESTMENT 5 YEARS LATER. Let P=______, r=_______, k=_____, and t=_____

JONATHON HAS $500 TO INVEST AT 9% ANNUAL INTEREST COMPOUNDED MONTHLY. HOW LONG WILL IT TAKE FOR HIS INVESTMENT TO GROW TO $3000?

WORK WITH A PARTNER: Pg. 341 #1 -8, 21 -22