Chapter 3 Exponential and Logarithmic Functions 3 1













- Slides: 25

Chapter 3 Exponential and Logarithmic Functions 3. 1 Exponential Functions Copyright © 2014, 2010, 2007 Pearson Education, Inc. 1

Objectives: • • Evaluate exponential functions. Graph exponential functions. Evaluate functions with base e. Use compound interest formulas. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 2

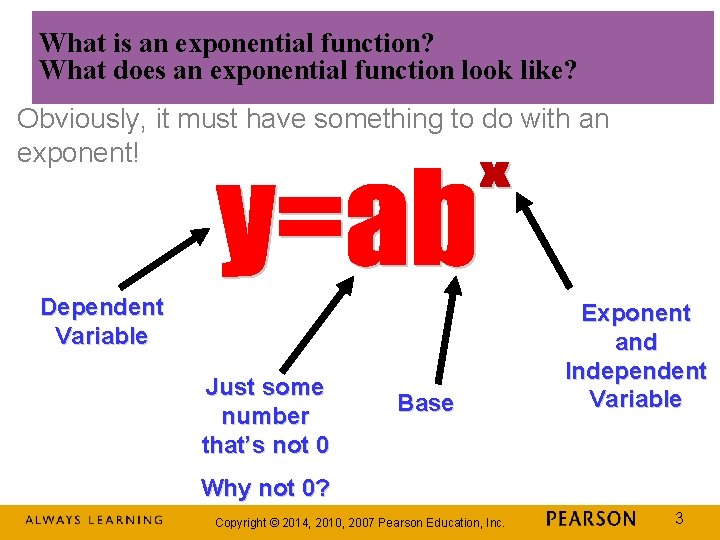
What is an exponential function? What does an exponential function look like? Obviously, it must have something to do with an exponent! Dependent Variable Just some number that’s not 0 Base Exponent and Independent Variable Why not 0? Copyright © 2014, 2010, 2007 Pearson Education, Inc. 3

The Basis of Bases The base carries the meaning of the function. 1) determines exponential growth or decay. 2)base is a positive number; however, it cannot be 1. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 4

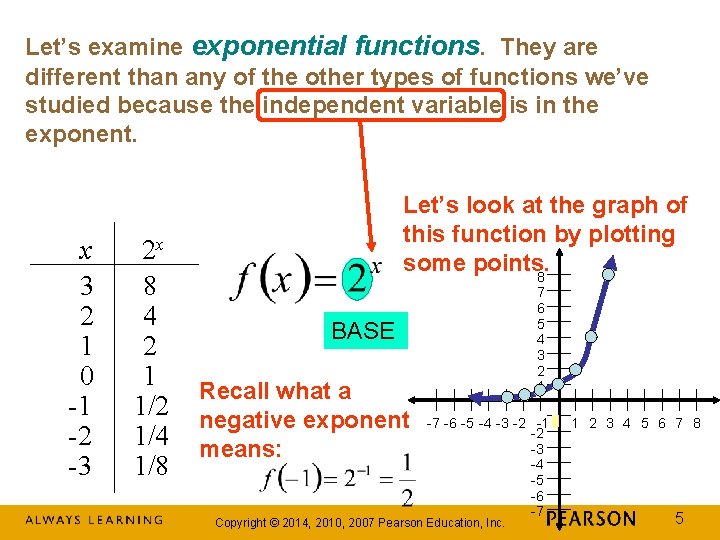
Let’s examine exponential functions. They are different than any of the other types of functions we’ve studied because the independent variable is in the exponent. x 3 2 1 0 -1 -2 -3 2 x 8 4 2 1 1/2 1/4 1/8 Let’s look at the graph of this function by plotting some points. 8 7 6 5 4 3 2 1 BASE Recall what a negative exponent means: -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -2 -3 -4 -5 -6 -7 Copyright © 2014, 2010, 2007 Pearson Education, Inc. 5

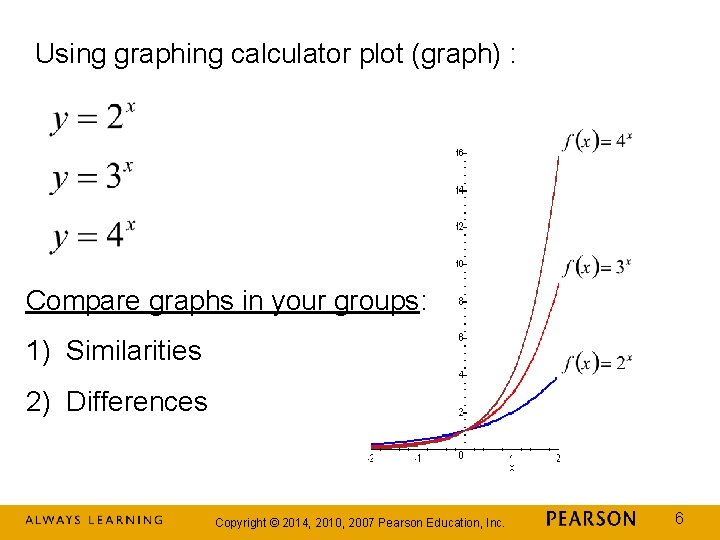
Using graphing calculator plot (graph) : Compare graphs in your groups: 1) Similarities 2) Differences Copyright © 2014, 2010, 2007 Pearson Education, Inc. 6

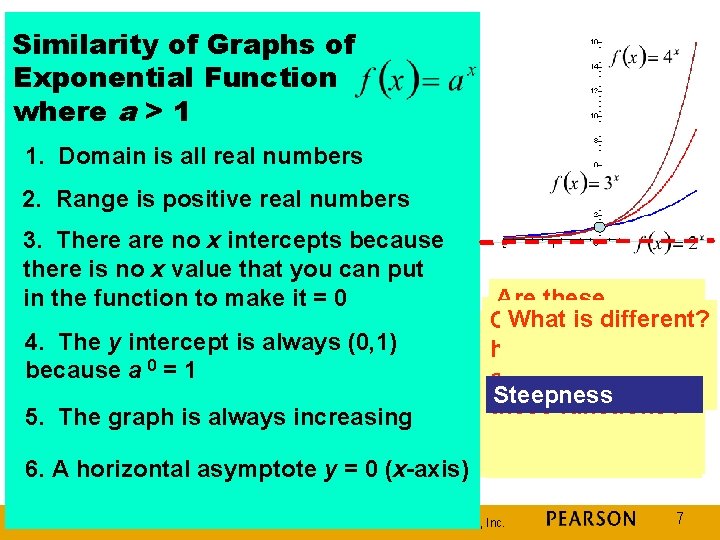
Similarity of Graphs of Exponential Function where a > 1 1. Domain is all real numbers 2. Range is positive real numbers 3. There are no x intercepts because there is no x value that you can put in the function to make it = 0 4. The y intercept is always (0, 1) because a 0 = 1 5. The graph is always increasing Are these What the What isisisthe range What different? Can you see the exponential What is the x What is the y domain of an exponential horizontal functions intercept ofthese exponential function? asymptote for increasing or exponential Steepness function? these functions? decreasing? functions? 6. A horizontal asymptote y = 0 (x-axis) Copyright © 2014, 2010, 2007 Pearson Education, Inc. 7

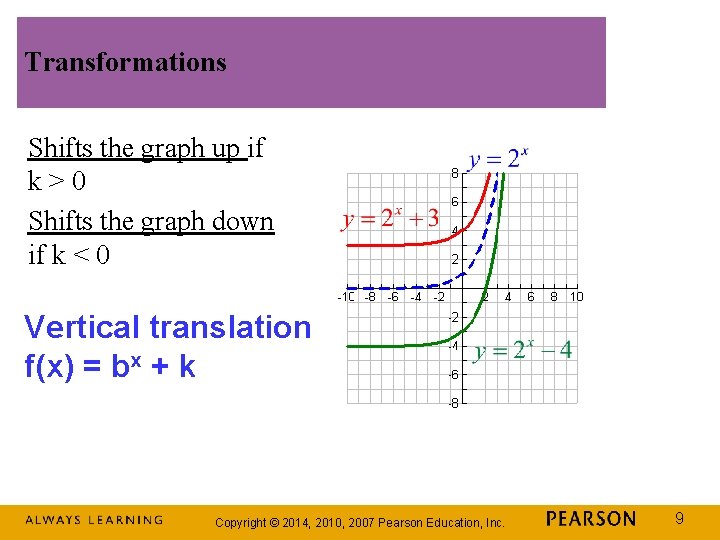
Graphing Exponential functions by Transformations What do you remember about Transformations of any functions: ---- shifts, reflections, stretching, compressing Coefficients/constants “a”, “h” and “k” On your graphing calculators : Copyright © 2014, 2010, 2007 Pearson Education, Inc. 8

Transformations Shifts the graph up if k>0 Shifts the graph down if k < 0 Vertical translation f(x) = bx + k Copyright © 2014, 2010, 2007 Pearson Education, Inc. 9

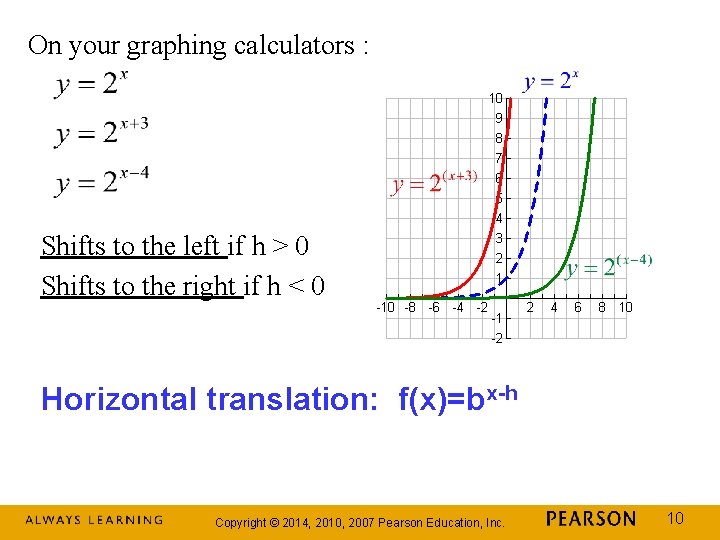
On your graphing calculators : Shifts to the left if h > 0 Shifts to the right if h < 0 Horizontal translation: f(x)=bx-h Copyright © 2014, 2010, 2007 Pearson Education, Inc. 10

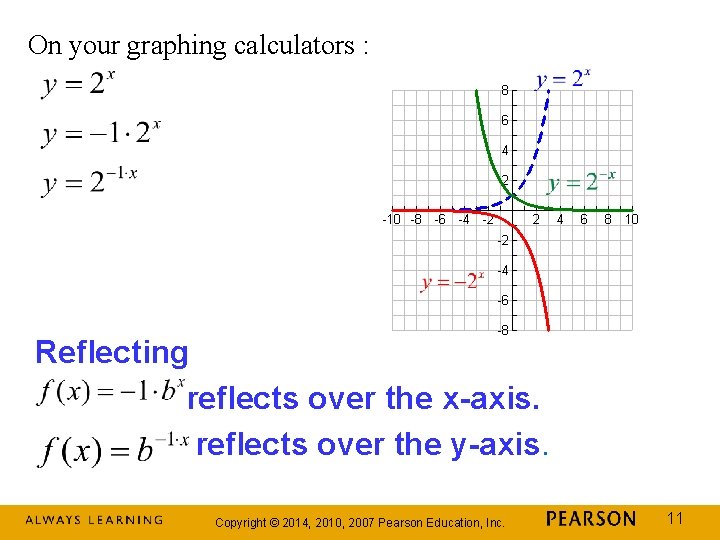
On your graphing calculators : Reflecting reflects over the x-axis. reflects over the y-axis. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 11

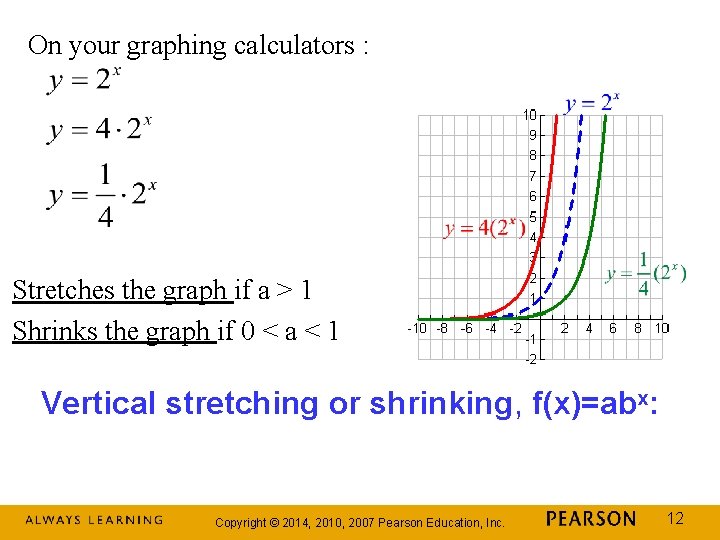
On your graphing calculators : Stretches the graph if a > 1 Shrinks the graph if 0 < a < 1 Vertical stretching or shrinking, f(x)=abx: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 12

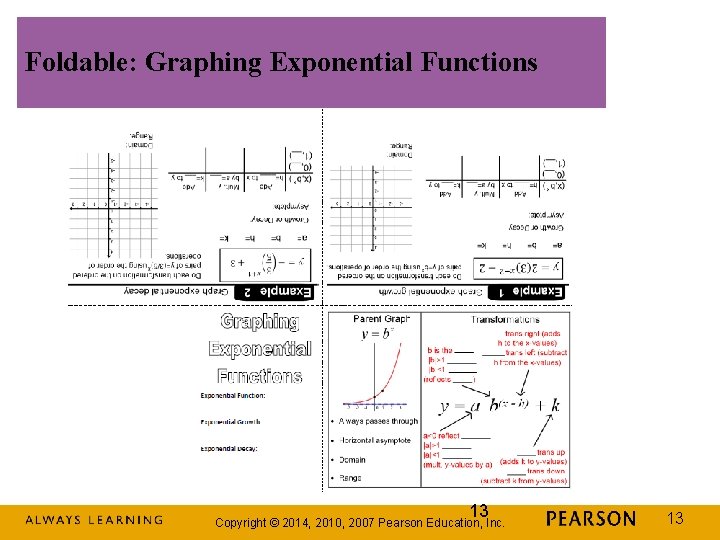
Foldable: Graphing Exponential Functions 13 Copyright © 2014, 2010, 2007 Pearson Education, Inc. 13

Let’s take a second look at the base of an exponential function. (It can be helpful to think about the base as the object that is being multiplied by itself repeatedly. ) Why can’t the base be negative? Why can’t the base be zero? Why can’t the base be one? Copyright © 2014, 2010, 2007 Pearson Education, Inc. 14

Copyright © 2014, 2010, 2007 Pearson Education, Inc. 15

Example: Evaluating an Exponential Function The exponential function models the average amount spent, f(x), in dollars, at a shopping mall after x hours. What is the average amount spent, to the nearest dollar, after three hours at a shopping mall? We substitute 3 for x and evaluate the function. After 3 hours at a shopping mall, the average amount spent is $160. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 16

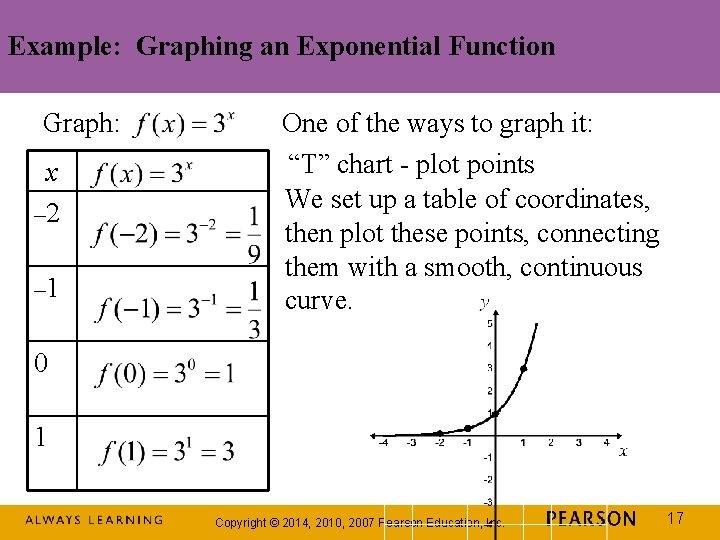
Example: Graphing an Exponential Function Graph: x – 2 – 1 One of the ways to graph it: “T” chart - plot points We set up a table of coordinates, then plot these points, connecting them with a smooth, continuous curve. 0 1 Copyright © 2014, 2010, 2007 Pearson Education, Inc. 17

Characteristics of Exponential Functions of the Form Copyright © 2014, 2010, 2007 Pearson Education, Inc. 18

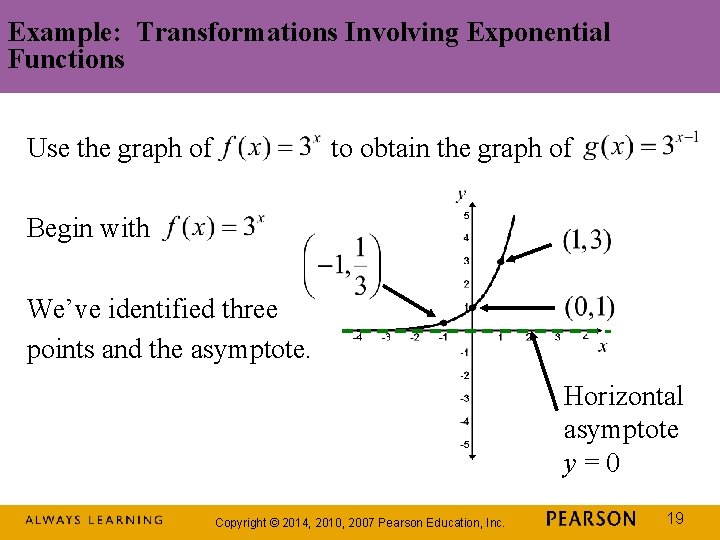
Example: Transformations Involving Exponential Functions Use the graph of to obtain the graph of Begin with We’ve identified three points and the asymptote. Horizontal asymptote y=0 Copyright © 2014, 2010, 2007 Pearson Education, Inc. 19

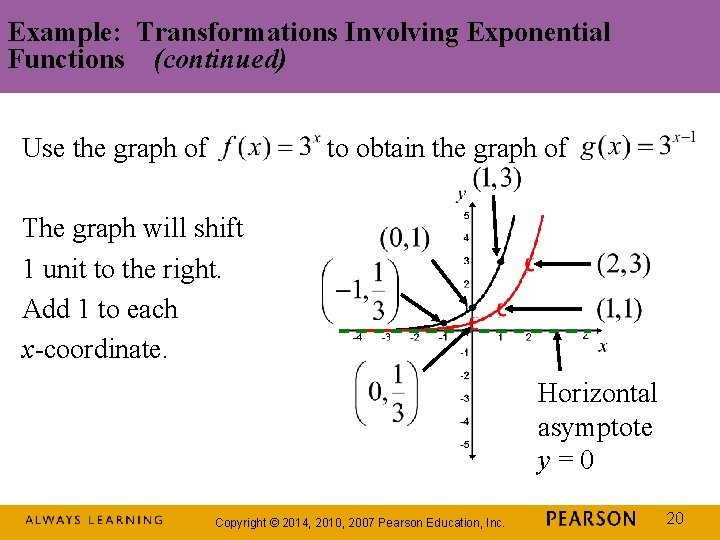
Example: Transformations Involving Exponential Functions (continued) Use the graph of to obtain the graph of The graph will shift 1 unit to the right. Add 1 to each x-coordinate. Horizontal asymptote y=0 Copyright © 2014, 2010, 2007 Pearson Education, Inc. 20

The Natural Base e The number e is defined as the value that approaches as n gets larger and larger. As the approximate value of e to nine decimal places is The irrational number, e, approximately 2. 72, is called the natural base. The function is called the natural exponential function. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 21

Example: Evaluating Functions with Base e The exponential function models the gray wolf population of the Western Great Lakes, f(x), x years after 1978. Project the gray wolf’s population in the recovery area in 2012. Because 2012 is 34 years after 1978, we substitute 34 for x in the given function. This indicates that the gray wolf population in the Western Great Lakes in the year 2012 is projected to be approximately 4446. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 22

Formulas for Compound Interest After t years, the balance, A, in an account with principal P and annual interest rate r (in decimal form) is given by the following formulas: 1. For n compounding periods per year: 2. For continuous compounding: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 23

Example: Using Compound Interest Formulas A sum of $10, 000 is invested at an annual rate of 8%. Find the balance in the account after 5 years subject to quarterly compounding. We will use the formula for n compounding periods per year, with n = 4. The balance of the account after 5 years subject to quarterly compounding will be $14, 859. 47. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 24

Example: Using Compound Interest Formulas A sum of $10, 000 is invested at an annual rate of 8%. Find the balance in the account after 5 years subject to continuous compounding. We will use the formula for continuous compounding. The balance in the account after 5 years subject to continuous compounding will be $14, 918. 25. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 25