Chapter 3 Experimental Error Significant figures Precision Reproducibility

Chapter 3 Experimental Error

- Significant figures - Precision (Reproducibility) - Accuracy (Error) - Uncertainty

3 -1 Significant Figures § Significant figures: minimum number of digits required to express a value in scientific notation without loss of accuracy (with the appropriate accuracy). Guidelines for Sig. Figs. , when looking at a number 1) All nonzero digits are significant figures 142. 7 = 1. 427 x 102 0. 000006302 = 6. 302 x 10 -6 Zeros are simple place holders 4 significant figures (sf) 9. 25 x 104 (3 sf) 9. 250 x 104 (4 sf) 92500 9. 2500 x 104 (5 sf) 2) Zeros are counted as significant figures only if: i) occur between other digits in the number (3 sf) 106 0. 0106 0. 106 ii) occur at the end of a number on the right-hand side of the decimal point 0. 1060 (4 sf)

The number of significant figures is the minimum number of digits needed to write a given value in scientific notation without loss of precision. 92, 500 9. 25 × 104 9. 2500 × 104 3 significant figures 4 significant figures 5 significant figures Zeros are significant 1) in the middle of a number, 2) at the end of a number on the right-hand side of a decimal point.

3 -2 Significant Figures in Arithmetic How many digits to retain in the answer after you have performed arithmetic operations with your data? Addition and Subtraction: the same decimal place in the final answer 1. 362 × 10 -4 + 3. 111 × 10 -4 4. 473 × 10 -4 5. 345 + 6. 728 12. 073 7. 26 × 10 14 -6. 69 × 10 14 0. 57 × 10 14 18. 9984032 (F) + 83. 789 (Kr) 121. 794 8064 1. 632 × 105 +4. 107 × 103 +0. 984 × 106 1. 632 × +0. 04107 × +9. 84 × 11. 51 × 105 105

- Multiplication and Division In multiplication and division, we are normally limited to the number of digits contained in the number with the fewest significant figures. 3. 26 × 10 -5 × 1. 78 5. 80 × 10 -5 4. 3179 × 1012 × 3. 6 × 10 -19 1. 6 × 10 -6 34. 60 ÷ 2. 46287 14. 05 - Logarithms and antilogarithms IF n = 10 a, then we say that a is the base 10 logarithm of n :

A logarithm is composed of a characteristic and a mantissa. The characteristic is the integer part and the mantissa is the decimal part log 339=2. 530 log 3. 39× 10 -5= -4. 470 Characteristic Mantissa =2 =0. 530 Characteristic Mantissa =-4 =0. 470 10 2. 531 =340(339. 6) 10 2. 530 =339(338. 8) 10 2. 529 =338(338. 1) antilog (-3. 42) = 10 -3. 42 = 3. 8 × 10 -4 log 0. 001237= -2. 9076 Log 1 237= 3. 0924 Log 3. 2=0. 51 antilog 4. 37=2. 3 × 10 4 10 -2. 600=2. 51 × 10 -3

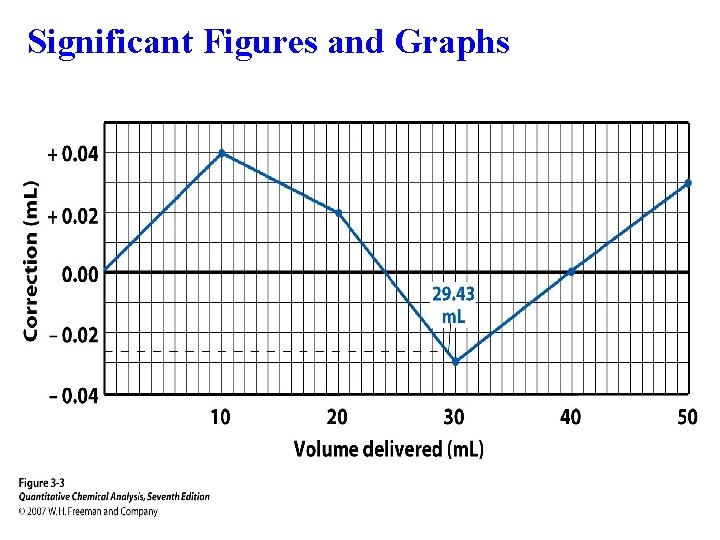
Significant Figures and Graphs

3 -3 Types of Error Experimental error from uncertainties of measurements - SYSTEMATIC ERROR: Systematic error , also called determinate error arises from a flaw in equipment or the design of experiment. - RANDOM ERROR: called indeterminate error arises from uncontrolled (and maybe uncontrollable) (GROSS ERRORS) ⇒ mainly originated by person ⇒ statistical calibration

Systematic errors: determinate error ⇒ definite value, assignable cause. ⇒ bias -> 모든 결과에 같은 크기의 영향을 미치며, 부호를 가짐. Box 3 -1. Case study : systematic error in Ozone Measurement

Sources of systematic errors Three types of systematic errors 1) instrumental errors 2) method errors 3) personal errors

■ Instrumental errors ⇒ measuring device error Ex) ① Pipet, burette, mass flask, etc. Reasons : The calibration temp. is nonequal to the measuring temp. Dry or heating cause the distortion of glass Contamination inside surface of vassel ② Electronic instrument error Reasons: potential change by dry cell life time Wrong calibration electric devise error by temperature change Noise from AC power source ③ Instrument operation in error conditions 이유: p. H meter in strong acid solutions -> acid error ⇒ vibration → detectable, correctable

■ Method errors ⇒ From nonideal behaviors of reactions and reagents. ⇒ Slow reaction, incomplete reaction, using unstable chemical, nonselectiveity of reagents, side reactions, etc. . ⇒ The most difficult to remove it. Ex) using excess reagents - Due to chemical properties of nicotinic acid – degradation using hot and conc. H 2 SO 4 - pyridine ring bearing nicotinic acid -> incomplete degradation. - Addition of potassium sulfate and elevate the boilng temp. -> complete degradation.

■ Personal errors ⇒ personal decision needs in many measurements. ⇒ error, toward one direction 예) • Reading in position of pointer between two points. • Color at the end point • liquid level of burret • Color sensitivity ⇒ personal bias 예) • 정밀도를 증가시키는 방향으로 눈금을 읽을 때 • 측정의 참값을 미리 마음 속으로 정해 놓을 때 • 숫자에 대한 편견이 있을 때 - 눈금 위의 바늘의 위치를 읽을 때 숫자 0과 5를 선호, - 큰 수보다 작은 수, - 홀수보다 짝수 선호

Detection of systematic instrumental & personal errors ⇒ Instrumental error • can be founded and corrected by calibration • periodical calibration • Instrumental error by interferences in samples → 단순한 검정으로 영향제거 불가능 ⇒ Personal error • It can be minimize by precaution, excise, etc. • Check instrument reading, notebook entries & calculations • chose the adequate method -- error minimizing

http: //www. nist. gov/

http: //ts. nist. gov/measurementservices/referencematerials/index. cfm

105. 4 Toxic Substances in Urine (powder form) SRMs 2670 a, 2671 a and 2672 a are for determining toxic substances in human urine. They consist of freeze-dried urine and are provided in sets of four 30 m. L bottles -- two each at low and elevated levels. NOTE: The values listed for these SRMs apply only to reconstituted urine.

■ Blank determinations ⇒ blank • reagents and solvents without analyte. • Similar condition of analyte environment (sample matrix): - >addition of sample constituents. ⇒ blank determination • every step in analysis : blank material analysis needs.

Precision and Accuracy Precision describes the reproducibility of a result, if you measure A quantity several time and the values agree closely with on another your measurement is precise. Accrue describes how close a measured value is to the “true” value If a known stands is available , accuracy hoe close your value is to the known value.

Precision ⇒ 측정의 재현성(reproducibility of measurements) ⇒ 정확히 똑같은 방법을 이용하여 얻은 측정값들 사이의 일치성 ⇒ 반복시료를 사용하여 반복적인 측정을 함 • Three terms to describe the precision - Standard deviation - Variance - Coefficient of variance (분산계수) ⇒ deviation from the mean (di)의 함수.

Absolute and Relative uncertainty Absolute uncertainty expresses the margin of uncertainty associated with a measurement. Relative uncertainty compares the size of the absolute uncertainty with the size of its associated measurement.

3 -4 Propagation of Uncertainty from Random Error We can usually estimate or measure the random error associated with measurement, such as the length of an object or the temperature of a solution. - Addition and Subtraction 1. 76 (± 0. 03) + 1. 89 (± 0. 02) -0. 59(± 0. 02) 3. 06(±e 4) e 1 e 2 e 3 Percent relative uncertainty=0. 041 / 3. 06 × 100= 1. 3% 3. 06 (± 0. 04): absolute uncertainty, 3. 06 (± 1 %): relative uncertainty

(EXAMPLE) Uncertainty in a Buret Reading

-Multiplication and Division

- Mixed Operations

Exponents and logarithms Uncertainty for powers and roots: (3 -7) Uncertainty for logarithm: Uncertainty for Natural logarihm Uncertainty For 10 x: Uncertainty for ex (3 -8) (3 -9) (3 -10) (3 -11)

3 -5 Propagation of Uncertainty from Systematic Error The standard deviation ( defined in section 4 -1 ) for this distribution, Also called the standard uncertainty , is ±a√ 3= ± 0. 0003/ √ 3= ± 0. 00017

Uncertainty in molecular mass

- Uncertainty in Molecular Mass

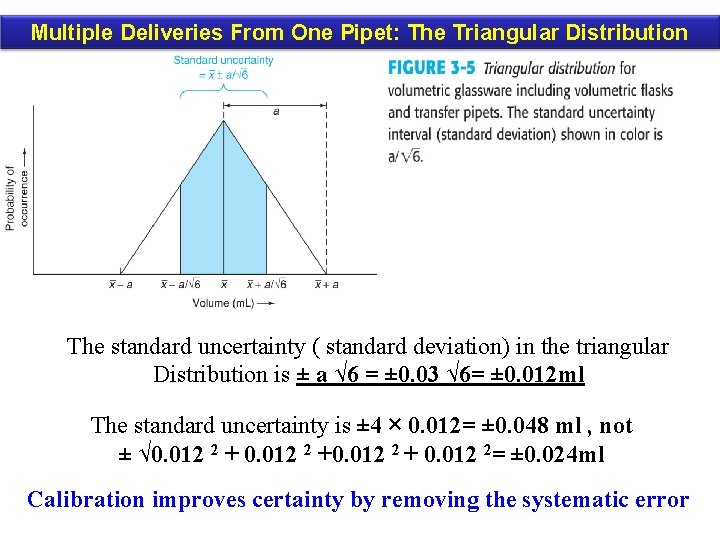
Multiple Deliveries From One Pipet: The Triangular Distribution The standard uncertainty ( standard deviation) in the triangular Distribution is ± a √ 6 = ± 0. 03 √ 6= ± 0. 012 ml The standard uncertainty is ± 4 × 0. 012= ± 0. 048 ml , not ± √ 0. 012 2 +0. 012 2 + 0. 012 2= ± 0. 024 ml Calibration improves certainty by removing the systematic error