Chapter 3 Equilibrium of a Particle Engineering Mechanics

Chapter 3: Equilibrium of a Particle Engineering Mechanics: Statics

Chapter Objectives To introduce the concept of the free-body diagram for a particle. l To show to solve particle equilibrium problems using the equations of equilibrium. l

Chapter Outline l Condition for the Equilibrium of a Particle l The Free-Body Diagram l Coplanar Systems l Three-Dimensional Force Systems

3. 1 Condition for the Equilibrium of a Particle at equilibrium if - At rest - Moving at constant a constant velocity l Newton’s first law of motion ∑F = 0 where ∑F is the vector sum of all the forces acting on the particle l

3. 1 Condition for the Equilibrium of a Particle Newton’s second law of motion ∑F = ma l When the force fulfill Newton's first law of motion, ma = 0 a=0 therefore, the particle is moving in constant velocity or at rest l

3. 2 The Free-Body Diagram Best representation of all the unknown forces (∑F) which acts on a body l A sketch showing the particle “free” from the surroundings with all the forces acting on it l Consider two common connections in this subject – Spring – Cables and Pulleys l

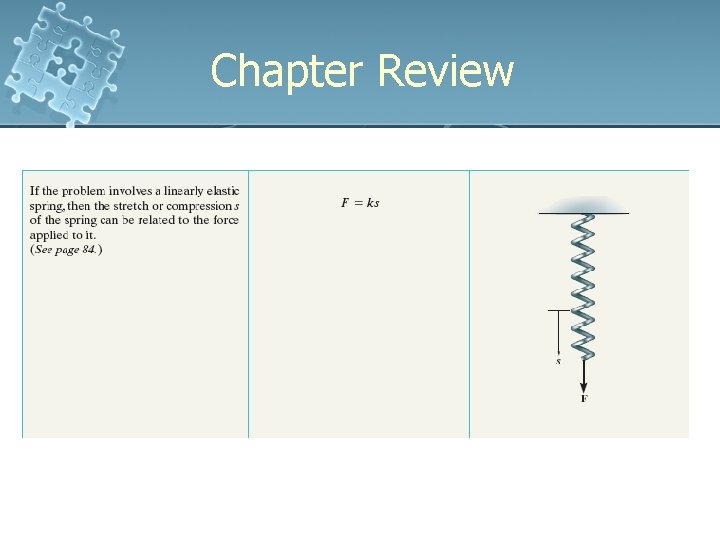
3. 2 The Free-Body Diagram l Spring - Linear elastic spring: change in length is directly proportional to the force acting on it - spring constant or stiffness k: defines the elasticity of the spring - Magnitude of force when spring is elongated or compressed F = ks

3. 2 The Free-Body Diagram l Spring where s is determined from the difference in spring’s deformed length l and its undeformed length lo s = l - lo - If s is positive, F “pull” onto the spring - If s is negative, F “push” onto the spring

3. 2 The Free-Body Diagram Example Given lo = 0. 4 m and k = 500 N/m To stretch it until l = 0. 6 m, A force, F = ks =(500 N/m)(0. 6 m – 0. 4 m) = 100 N is needed To compress it until l = 0. 2 m, A force, F = ks =(500 N/m)(0. 2 m – 0. 4 m) = -100 N is needed

3. 2 The Free-Body Diagram l Cables and Pulley - Cables (or cords) are assumed to have negligible weight and they cannot stretch - A cable only support tension or pulling force - Tension always acts in the direction of the cable - Tension force in a continuous cable must have a constant magnitude for equilibrium

3. 2 The Free-Body Diagram l Cables and Pulley - For any angle θ, the cable is subjected to a constant tension T throughout its length

3. 2 The Free-Body Diagram Procedure for Drawing a FBD 1. Draw outlined shape - Isolate particle from its surroundings 2. Show all the forces - Indicate all the forces - Active forces: set the particle in motion - Reactive forces: result of constraints and supports that tend to prevent motion

3. 2 The Free-Body Diagram Procedure for Drawing a FBD 3. Identify each forces - Known forces should be labeled with proper magnitude and direction - Letters are used to represent magnitude and directions of unknown forces

3. 2 The Free-Body Diagram l l A spool is having a weight W which is suspended from the crane bottom Consider FBD at A since these forces act on the ring Cables AD exert a resultant force of W on the ring Condition of equilibrium is used to obtained TB and TC

3. 2 The Free-Body Diagram l l l The bucket is held in equilibrium by the cable Force in the cable = weight of the bucket Isolate the bucket for FBD Two forces acting on the bucket, weight W and force T of the cable Resultant of forces = 0 W=T

3. 2 The Free-Body Diagram Example 3. 1 The sphere has a mass of 6 kg and is supported. Draw a free-body diagram of the sphere, the cord CE and the knot at C.

3. 2 The Free-Body Diagram View Free Body Diagram Solution FBD at Sphere l Two forces acting, weight and the force on cord CE. l Weight of 6 kg (9. 81 m/s 2) = 58. 9 N

3. 2 The Free-Body Diagram Solution Cord CE l Two forces acting, force of the sphere and force of the knot l Newton’s Third Law: FCE is equal but opposite l FCE and FEC pull the cord in tension l For equilibrium, FCE = FEC

3. 2 The Free-Body Diagram Solution FBD at Knot l Three forces acting, force by cord CBA, cord CE and spring CD l Important to know that the weight of the sphere does not act directly on the knot but subjected to by the cord CE

3. 3 Coplanar Systems l l l A particle is subjected to coplanar forces in the x-y plane Resolve into i and j components for equilibrium ∑Fx = 0 ∑Fy = 0 Scalar equations of equilibrium require that the algebraic sum of the x and y components to equal o zero

3. 3 Coplanar Systems l Scalar Notation - Sense of direction = an algebraic sign that corresponds to the arrowhead direction of the component along each axis - For unknown magnitude, assume arrowhead sense of the force - Since magnitude of the force is always positive, if the scalar is negative, the force is acting in the opposite direction

3. 3 Coplanar Systems Example Consider the free-body diagram of the particle subjected to two forces l l Assume unknown force F acts to the right for equilibrium ∑Fx = 0 ; + F + 10 N = 0 F = -10 N Force F acts towards the left for equilibrium

3. 3 Coplanar Systems l l l The chain exerts three forces on the ring at A. The ring will not move, or will move with constant velocity, provided the summation of the forces along the y axis is zero With any force known, the magnitude of other two forces are found by equations of equilibrium

3. 3 Coplanar Systems l Procedure for Analysis 1. Free-Body Diagram - Establish the x, y axes in any suitable orientation - Label all the unknown and known forces magnitudes and directions - Sense of the unknown force can be assumed

3. 3 Coplanar Systems l Procedure for Analysis 2) Equations of Equilibrium - Given two unknown with a spring, apply F = ks to find spring force using deformation of spring - If the solution yields a negative result, the sense of force is the reserve of that shown in the free-body diagram

3. 3 Coplanar Systems l Procedure for Analysis 2) Equations of Equilibrium - Apply the equations of equilibrium ∑Fx = 0 ∑Fy = 0 - Components are positive if they are directed along the positive negative axis and negative, if directed along the negative axis

3. 3 Coplanar Systems Example 3. 2 Determine the tension in cables AB and AD for equilibrium of the 250 kg engine.

3. 3 Coplanar Systems Solution FBD at Point A - Initially, two forces acting, forces of cables AB and AD - Engine Weight = (250 kg)(9. 81 m/s 2) = 2. 452 k. N supported by cable CA - Finally, three forces acting, forces TB and TD and engine weight on cable CA

3. 3 Coplanar Systems Solution +→ ∑Fx = 0; +↑ ∑Fy = 0; Solving, TBcos 30° - TD = 0 TBsin 30° - 2. 452 k. N = 0 TB = 4. 90 k. N TD = 4. 25 k. N *Note: Neglect the weights of the cables since they are small compared to the weight of the engine

3. 3 Coplanar Systems Example 3. 3 If the sack at A has a weight of 20 N (≈ 2 kg), determine the weight of the sack at B and the force in each cord needed to hold the system in the equilibrium position shown.

3. 3 Coplanar Systems Solution FBD at Point E - Three forces acting, forces of cables EG and EC and the weight of the sack on cable EA

3. 3 Coplanar Systems Solution +→ ∑Fx = 0; +↑ ∑Fy = 0; Solving, TEGsin 30° - TECcos 45° = 0 TEGcos 30° - TECsin 45° - 20 N = 0 TEC = 38. 6 k. N TEG = 54. 6 k. N *Note: use equilibrium at the ring to determine tension in CD and weight of B with TEC known

3. 3 Coplanar Systems Solution FBD at Point C - Three forces acting, forces by cable CD and EC (known) and weight of sack B on cable CB

3. 3 Coplanar Systems Solution +→ ∑Fx = 0; +↑ ∑Fy = 0; Solving, 38. 6 cos 30° - (4/5)TCD = 0 (3/5)TCD – 38. 6 sin 45°N – WB = 0 TCD = 34. 1 k. N WB = 47. 8 k. N *Note: components of TCD are proportional to the slope of the cord by the 3 -4 -5 triangle

3. 4 Three-Dimensional Force Systems l l l For particle equilibrium ∑F = 0 Resolving into i, j, k components ∑ F x i + ∑ F yj + ∑ F z k = 0 Three scalar equations representing algebraic sums of the x, y, z forces ∑ F xi = 0 ∑ F yj = 0 ∑F zk = 0

3. 4 Three-Dimensional Force Systems l Make use of the three scalar equations to solve for unknowns such as angles or magnitudes of forces

3. 4 Three-Dimensional Force Systems l l l Ring at A subjected to force from hook and forces from each of the three chains Hook force = weight of the electromagnet and the load, denoted as W Three scalars equations applied to FBD to determine FB, FC and FD

3. 4 Three-Dimensional Force Systems l Procedure for Analysis Free-body Diagram - Establish the z, y, z axes in any suitable orientation - Label all known and unknown force magnitudes and directions - Sense of a force with unknown magnitude can be assumed

3. 4 Three-Dimensional Force Systems l Procedure for Analysis Equations of Equilibrium - Apply ∑Fx = 0, ∑Fy = 0 and ∑Fz = 0 when forces can be easily resolved into x, y, z components - When geometry appears difficult, express each force as a Cartesian vector. Substitute vectors into ∑F = 0 and set i, j, k components = 0 - Negative results indicate that the sense of the force is opposite to that shown in the FBD.

3. 4 Three-Dimensional Force Systems Example 3. 5 A 90 N load is suspended from the hook. The load is supported by two cables and a spring having a stiffness k = 500 N/m. Determine the force in the cables and the stretch of the spring for equilibrium. Cable AD lies in the x-y plane and cable AC lies in the x-z plane.

3. 4 Three-Dimensional Force Systems Solution FBD at Point A - Point A chosen as the forces are concurrent at this point

Solution Equations ∑Fx = 0; ∑Fy = 0; ∑Fz = 0; 3. 4 Three-Dimensional Force Systems of Equilibrium, FDsin 30° - (4/5)FC = 0 -FDcos 30° + FB = 0 (3/5)FC – 90 N = 0 Solving, FC = 150 N FD = 240 N FB = 208 N

3. 4 Three-Dimensional Force Systems Solution For the stretch of the spring, FB = ks. AB 208 N = 500 N/m(s. AB) s. AB = 0. 416 m

3. 4 Three-Dimensional Force Systems Example 3. 6 Determine the magnitude and coordinate direction angles of force F that are required for equilibrium of the particle O.

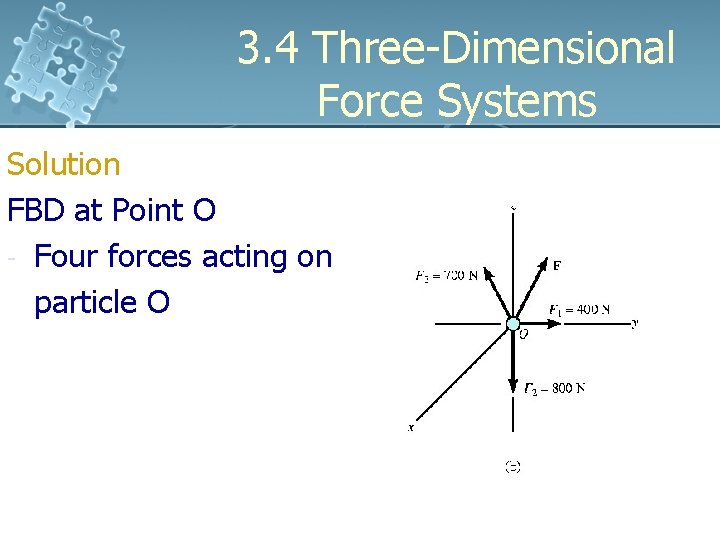
3. 4 Three-Dimensional Force Systems Solution FBD at Point O - Four forces acting on particle O

3. 4 Three-Dimensional Force Systems Solution Equations of Equilibrium Expressing each forces in Cartesian vectors, F 1 = {400 j} N F 2 = {-800 k} N F 3 = F 3(r. B / r. B) = {-200 i – 300 j + 600 k } N F = F x i + F yj + F z k

3. 4 Three-Dimensional Force Systems Solution For equilibrium, ∑F = 0; F 1 + F 2 + F 3 + F = 0 400 j - 800 k - 200 i – 300 j + 600 k + F x i + F yj + F z k = 0 ∑Fx = 0; - 200 + Fx = 0 Fx = 200 N ∑Fy = 0; 400 – 300 + Fy = 0 Fy = -100 N ∑Fz = 0; - 800 + 600 + Fz = 0 Fz = 200 N

3. 4 Three-Dimensional Force Systems Solution

3. 4 Three-Dimensional Force Systems Example 3. 7 Determine the force developed in each cable used to support the 40 k. N (≈ 4 tonne) crate.

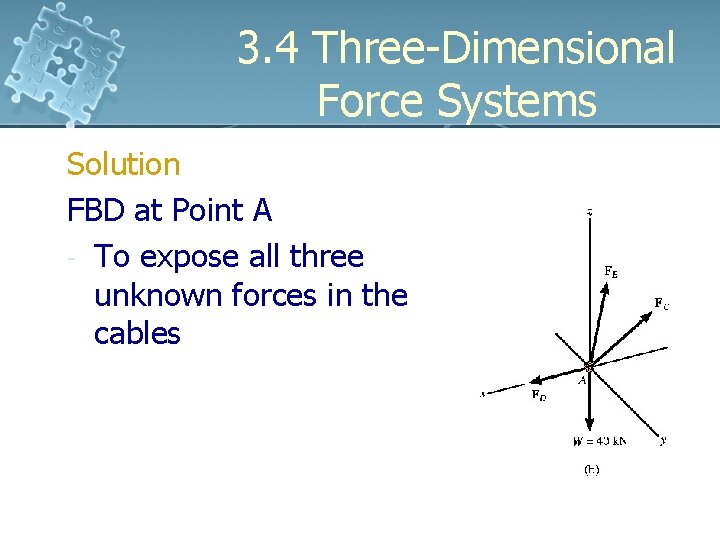
3. 4 Three-Dimensional Force Systems Solution FBD at Point A - To expose all three unknown forces in the cables

3. 4 Three-Dimensional Force Systems Solution Equations of Equilibrium Expressing each forces in Cartesian vectors, FB = FB(r. B / r. B) = -0. 318 FBi – 0. 424 FBj + 0. 848 FBk FC = FC (r. C / r. C) = -0. 318 FCi – 0. 424 FCj + 0. 848 FCk FD = F D i W = -40 k

3. 4 Three-Dimensional Force Systems Solution For equilibrium, ∑F = 0; FB + FC + FD + W = 0 -0. 318 FBi – 0. 424 FBj + 0. 848 FBk - 0. 318 FCi – 0. 424 FCj + 0. 848 FCk + FDi - 40 k =0 ∑Fx = 0; -0. 318 FB - 0. 318 FC + FD = 0 ∑Fy = 0; – 0. 424 FB – 0. 424 FC = 0 ∑Fz = 0; 0. 848 FB + 0. 848 FC - 40 = 0

3. 4 Three-Dimensional Force Systems Solution Solving, FB = FC = 23. 6 k. N FD = 15. 0 k. N

Chapter Summary Equilibrium l l A particle at rest or moving in constant velocity is in equilibrium All forces acting on a particle = 0 To account for all the forces, draw a free-body diagram FBD shows all the forces, with known or unknown magnitudes and directions

Chapter Summary Two Dimensional l Two scalars equations ∑Fx = 0 and ∑Fy = 0 is applied to x, y coordinate system If the solution is negative, the sense of the force is opposite to that shown on the FBD. If problem involves a linear spring, stretch or compression can be related to force by F = ks

Chapter Summary Three Dimensions l l l For 3 D problems, equilibrium equation ∑F = 0 should be applied using a Cartesian vector analysis First, express forces on the FBD as Cartesian vectors Second, sum the forces and equate the i, j and k components = 0 so that ∑Fx = 0, ∑Fy = 0 and ∑Fz = 0

Chapter Review

Chapter Review

Chapter Review

Chapter Review