CHAPTER 3 EQUILIBRIUM OF A PARTICAL Chapter Objectives

CHAPTER 3 EQUILIBRIUM OF A PARTICAL

Chapter Objectives i. Concept of the free-body diagram for a particle. ii. Solve particle equilibrium problems using the equations of equilibrium. iii. Coplanar force system.

Condition of Equilibrium Particle • Particle at equilibrium if - At rest, statics. - Moving at constant a constant velocity. • Newton’s first law of motion ∑F = 0 where ∑F is the vector sum of all the forces acting on the particle.

Condition of Equilibrium Particle • Newton’s second law of motion ∑F = ma • When the force fulfill Newton's first law of motion, ma = 0 a=0 therefore, the particle is moving in constant velocity or at rest.

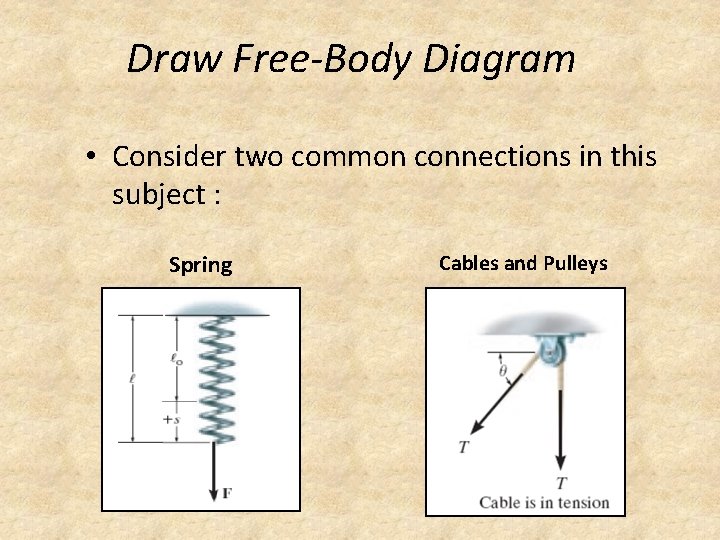
Draw Free-Body Diagram • Consider two common connections in this subject : Spring Cables and Pulleys

Draw Free-Body Diagram • Spring – Linear elastic spring: change in length is directly proportional to the force acting on it. – spring constant or stiffness k: defines the elasticity of the spring. – Magnitude of force when spring Linear elastic spring: is elongated or compressed. distance S = ∫ 1 – ∫ o F = ks Constant elasticity of the spring

Draw Free-Body Diagram • Cables and Pulley – Cables (or cords) are assumed negligible weight and cannot stretch. – Tension always acts in the direction of the cable. – Tension force must have a constant magnitude for equilibrium. – For any angle θ, the cable is subjected to a constant tension T.

Draw Free-Body Diagram Procedure for Drawing a FBD: 1. Draw outlined shape. 2. Show all the forces. 3. Identify each forces. Examples:

Example: The sphere has a mass of 6 kg and supported. Draw FBD of : (1) the sphere (2) the knot at C

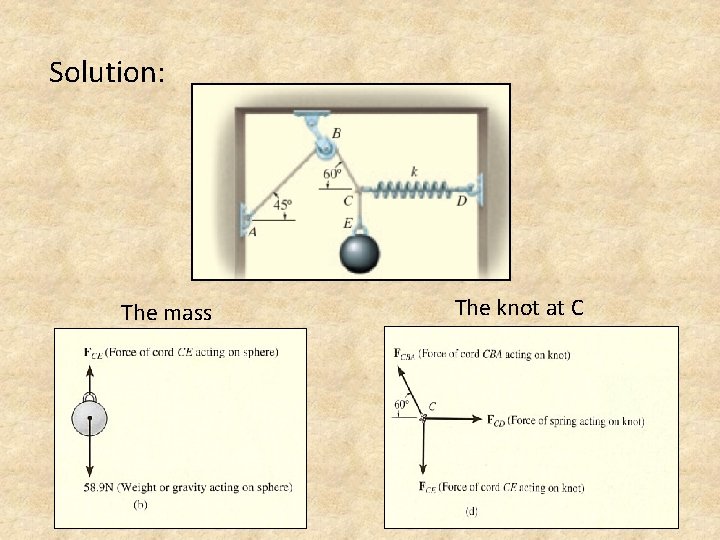
Solution: The mass The knot at C

Coplanar Force System • A particle is subjected to coplanar forces in the x -y plane. • Resolve into i and j components for equilibrium. • Scalar equations of equilibrium require that the algebraic sum of the x and y components to equal to zero. ∑Fx = 0 ∑Fy = 0

Coplanar Force System Procedure for Analysis: 1. Draw FBD. - Establish the x, y axes. - Label all the unknown and known forces. 2. Equations of Equilibrium. - Apply F = ks to find spring force. - When negative result force is the reserve. - Apply the equations of equilibrium. ∑Fx = 0 ∑Fy = 0

Example 1: Determine the tension in the cables AB and AD for equilibrium of the 350 kg engine shown in the figure below.

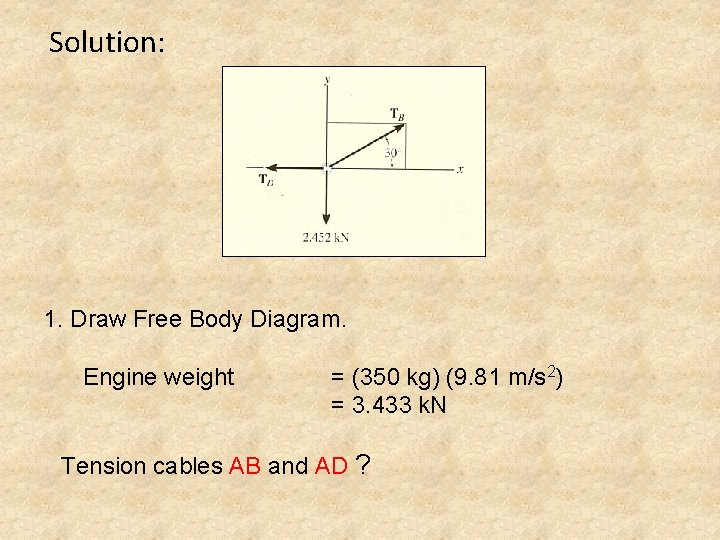
Solution: 1. Draw Free Body Diagram. Engine weight = (350 kg) (9. 81 m/s 2) = 3. 433 k. N Tension cables AB and AD ?

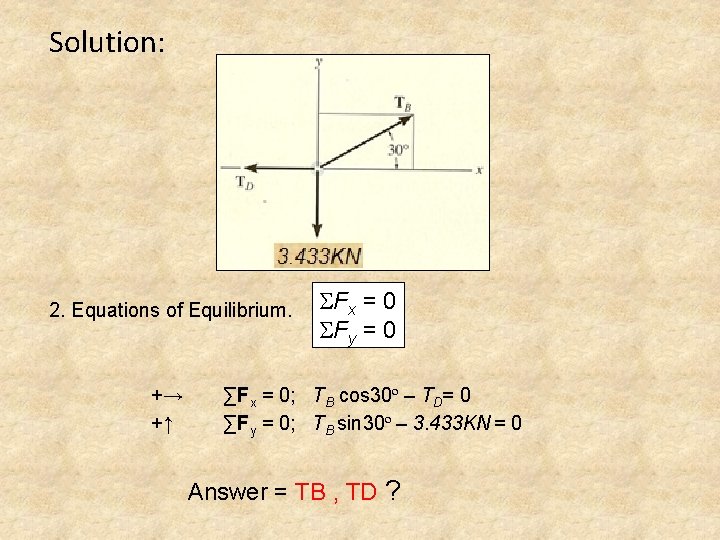
Solution: 2. Equations of Equilibrium. +→ +↑ SFx = 0 SFy = 0 ∑Fx = 0; TB cos 30º – TD= 0 ∑Fy = 0; TB sin 30º – 3. 433 KN = 0 Answer = TB , TD ?

Example 2: Determine the required length of the cord AC so that the 8 kg lamp is suspended. The undeformed length of the spring AB is l’AB = 0. 4 m, and the spring has a stiffness of k. AB = 300 N/m.

Solution: 1. Free Body Diagram. The lamp has a weight W = 8(9. 81) = 78. 5 N 2. Equations of Equilibrium. +→ ∑Fx = 0; TAB – TAC cos 30º = 0 +↑ ∑Fy = 0; TACsin 30º – 78. 5 N = 0 Solving, TAC = 157. 0 N ; TAB = 135. 9 N

Solution: TAB = k. ABs. AB ; 135. 9 N = 300 N/m(s. AB) s. AB = 0. 453 N For stretched length, l. AB = l’AB+ s. AB l. AB = 0. 4 m + 0. 453 m = 0. 853 m For horizontal distance BC, 2 m = l. ACcos 30° + 0. 853 m l. AC = 1. 32 m

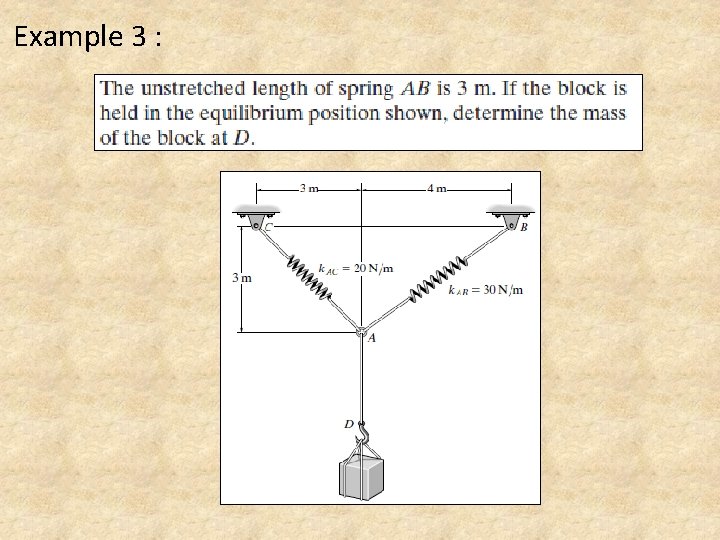
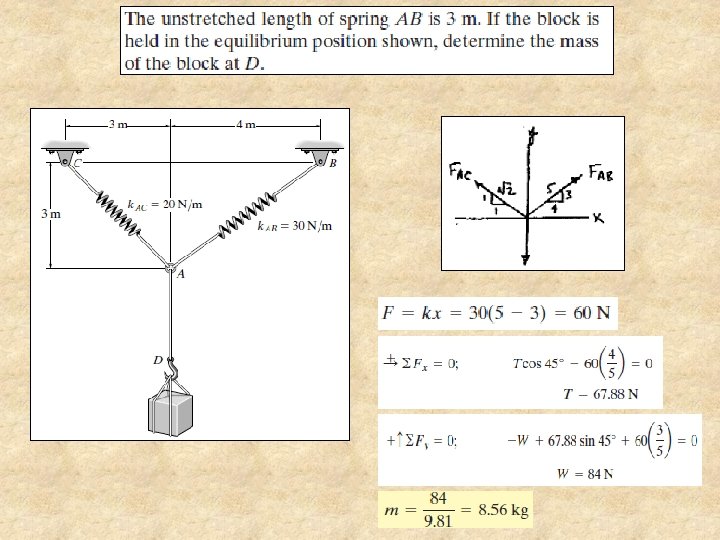
Example 3 :

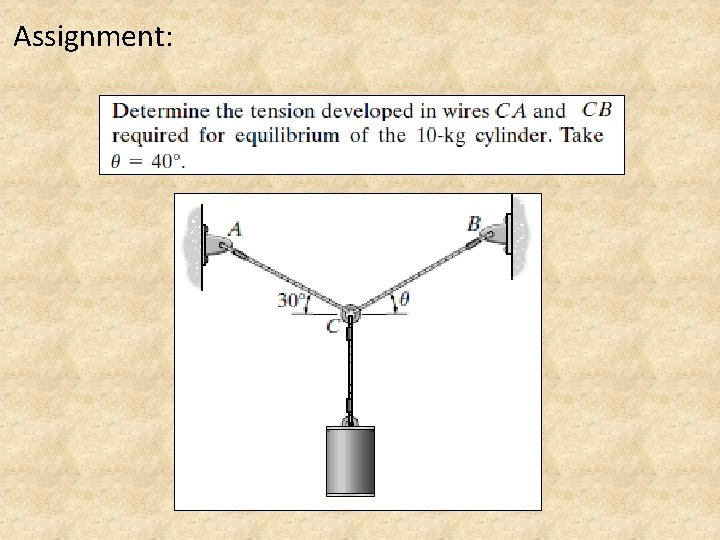
Assignment: