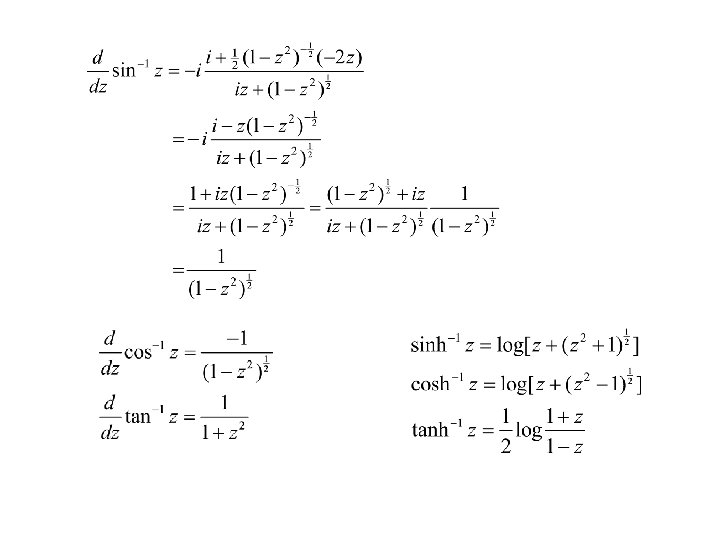Chapter 3 Elementary Functions Consider elementary functions studied





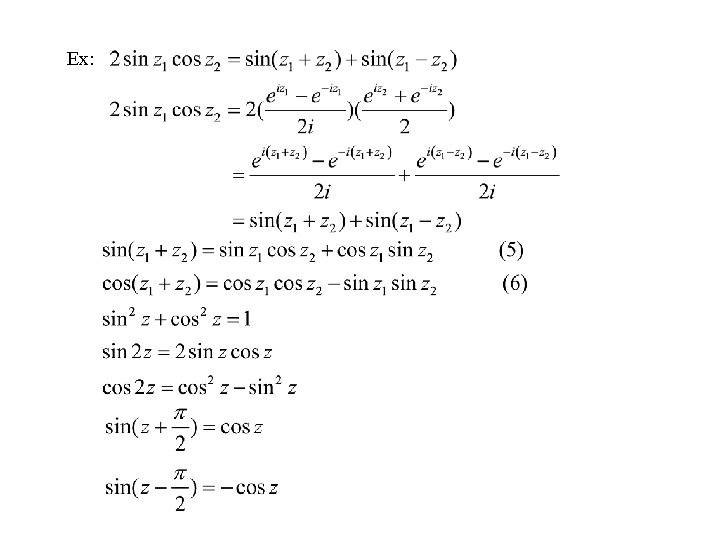






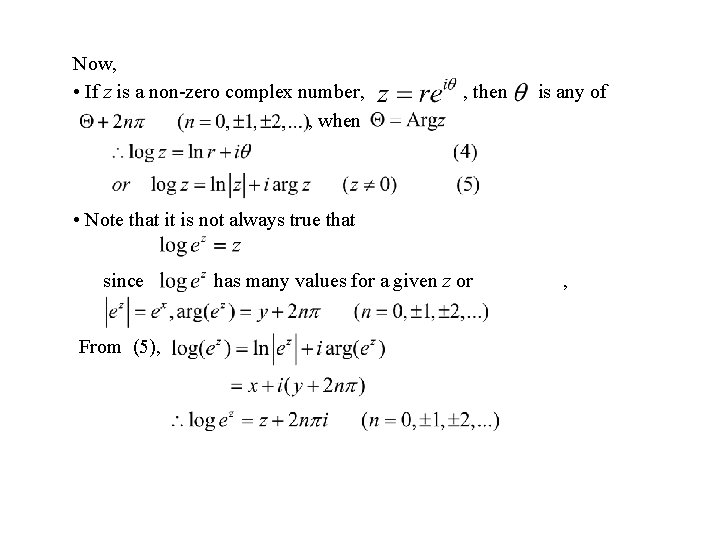





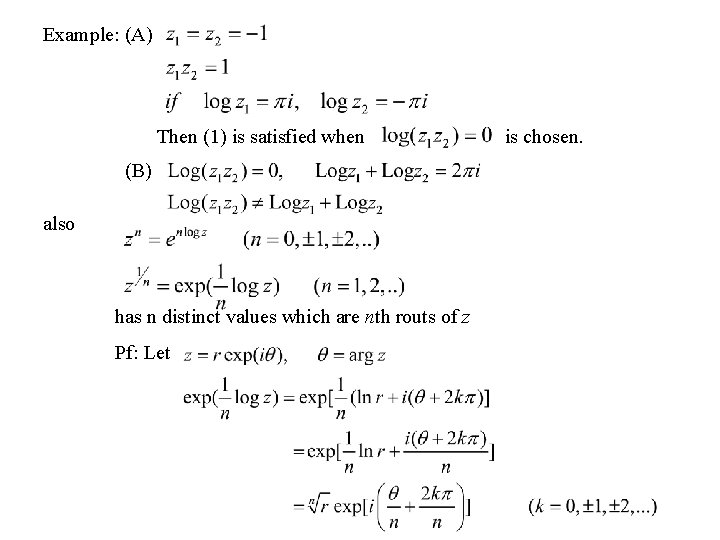




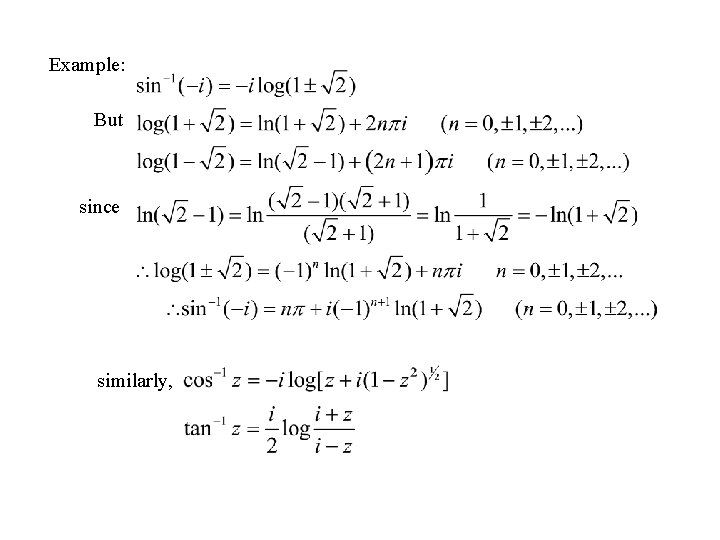
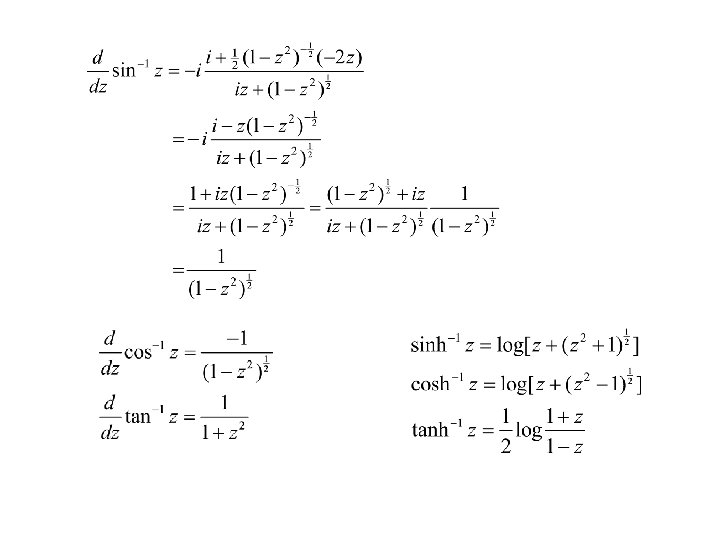
- Slides: 25

Chapter 3. Elementary Functions Consider elementary functions studied in calculus and define corresponding functions of a complex variable. To be specific, define analytic functions of a complex variable z that reduce to the elementary functions in calculus when z = x+i 0. 23. Exponential Function If f (z), i. e. is to reduce to for all real x, when z=x (1) It is natural to impose the following conditions: f is entire and for all z. (2) As shown in Ex. 1 of sec. 18 is differentiable everywhere in the complex plane and .

It can be shown that (Ex. 15) this is the only function satisfying conditions (1) and (2) And we write (3) (4) when (3) Euler’s Formula (5) since is positive for all x and since is always positive, for any complex number z.

• can be used to verify the additive property

Ex : There are values of z such that

24. Trigonometric Functions By Euler’s formula It is natural to define These two functions are entire since are entire.
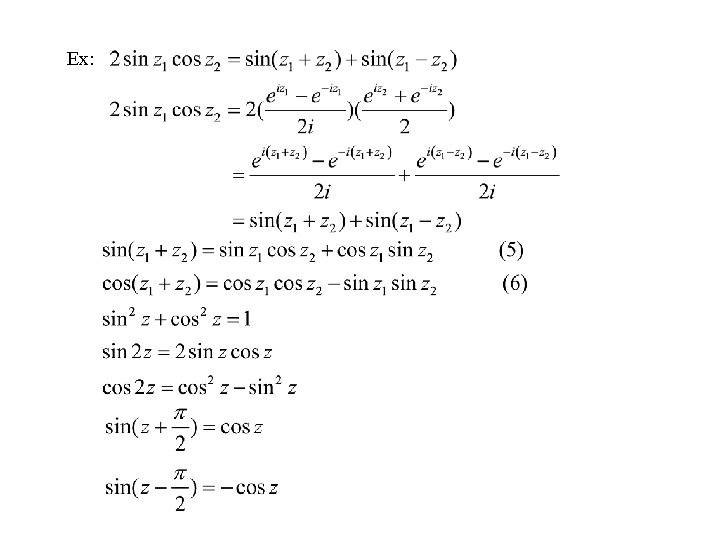
Ex:

when y is real. • in Exercise 7. unbounded

• A zero of a given function f (z) is a number z 0 such that f (z 0)=0 Since And there are no other zeros since from (15)

25. Hyperbolic Functions (3) (4)

Frequently used identities

• From (4), sinhz and coshz are periodic with period • • •

26. The Logarithmic Function and Its Branches 27. To solve Thus if we write
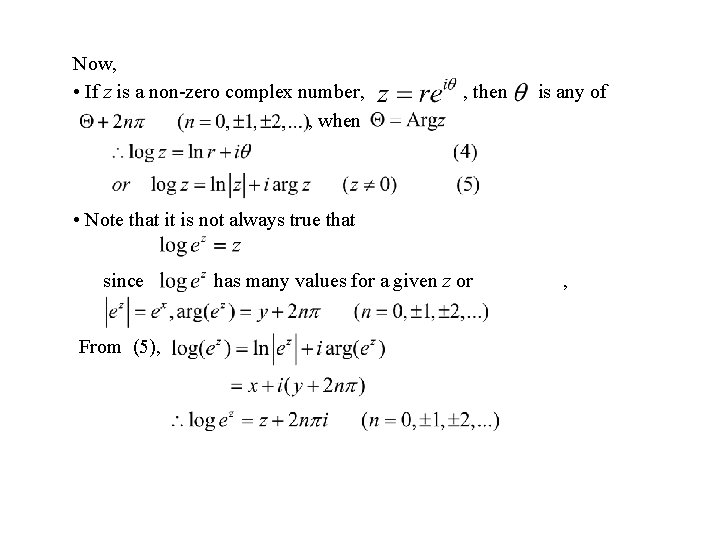
Now, • If z is a non-zero complex number, , when , then is any of • Note that it is not always true that since From (5), has many values for a given z or ,

The principal value of log z is obtained from (2) when n=0 and is denoted by

• If we let denote any real number and restrict the values of expression (4) to the interval then with components is single-valued and continuous in the domain. is also analytic, in



27. Some Identities Involving Logarithms non-zero. complex numbers (1) Pf:
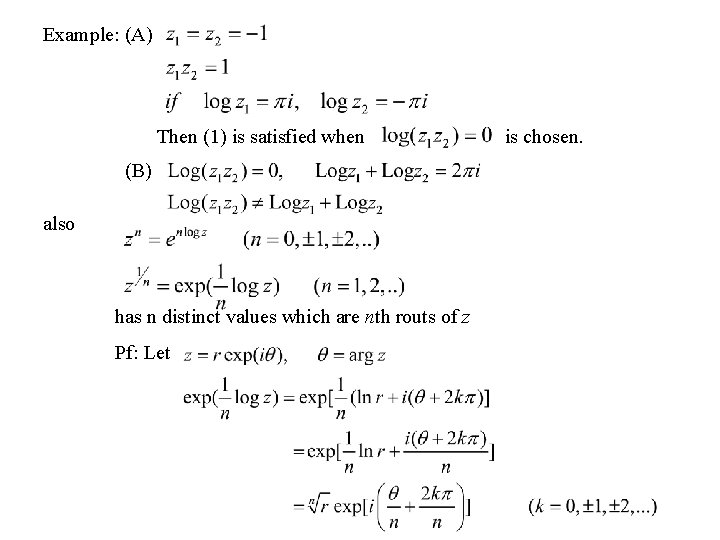
Example: (A) Then (1) is satisfied when (B) also has n distinct values which are nth routs of z Pf: Let is chosen.

28. Complex Exponents when , c is any complex number, is defined by where log z donates the multiple-valued log function. ( is already known to be valid when c=n and c=1/n ) Example 1: Powers of z are in general multi-valued. since

If and is any real number, the branch of the log function is single-valued analytic in the indicated domain. when that branch is used, is singled-valued analytic in the same domain.

Example 3. The principal value of It is analytic in the domain In (1) now define the exponential function with base C. when a value of logc is specified, is an entire function of z.

29. Inverse Trigonometric and Hyperbolic Functions 30. write Solving for taking log on both sides.
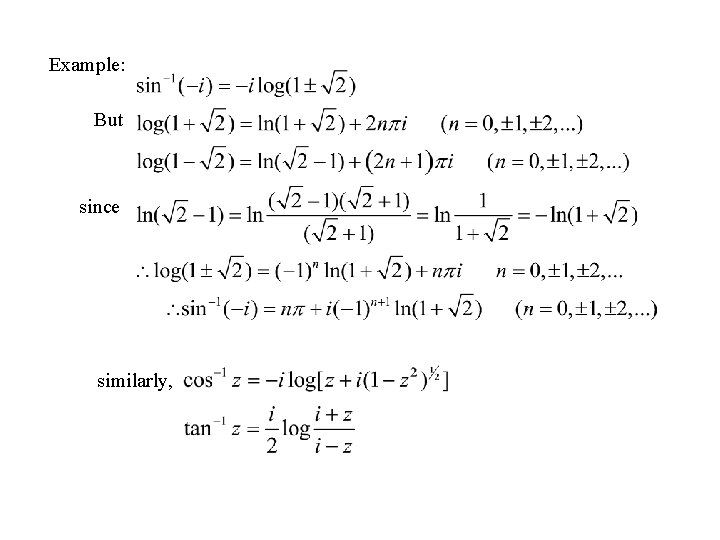
Example: But since similarly,