Chapter 3 Discrete Random Variables and Probability Distributions

Chapter 3 Discrete Random Variables and Probability Distributions § 3. 1 - Random Variables § 3. 2 - Probability Distributions for Discrete Random Variables § 3. 3 - Expected Values § 3. 4 - The Binomial Probability Distribution § 3. 5 - Hypergeometric and Negative Binomial Distributions § 3. 6 - The Poisson Probability Distribution
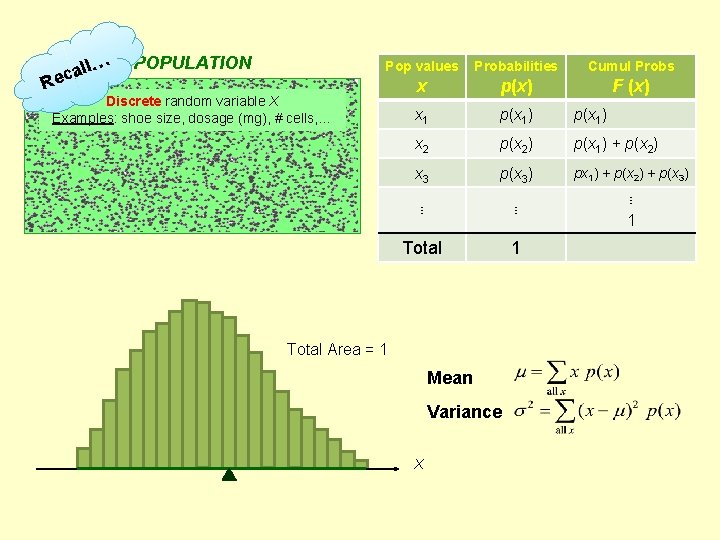
ll… a c Re POPULATION Pop values Probabilities Cumul Probs x p(x) F (x) x 1 p(x 1) x 2 p(x 2) p(x 1) + p(x 2) x 3 p(x 3) px 1) + p(x 2) + p(x 3) ⋮ ⋮ ⋮ 1 Total 1 Discrete random variable X Examples: shoe size, dosage (mg), # cells, … Total Area = 1 Mean Variance X

Classical Discrete Probability Distributions ● Binomial ~ X = # Successes in n trials, P(Success) = ● Poisson ~ As above, but n large, small, i. e. , Success RARE ● Negative Binomial ~ X = # trials for k Successes, P(Success) = ● Geometric ~ As above, but specialized to k = 1 ● Hypergeometric ~ As Binomial, but changes between trials ● Multinomial ~ As Binomial, but for multiple categories, with 1 + 2 + … + last = 1 and x 1 + x 2 + … + xlast = n

~ The Binomial Distribution ~ �Used only when dealing with binary outcomes (two categories: “Success” vs. “Failure”), with a fixed probability of Success ( ) in the population. �Calculates the probability of obtaining any given number of Successes in a random sample of n independent “Bernoulli trials. ” �Has many applications and generalizations, e. g. , multiple categories, variable probability of Success, etc.
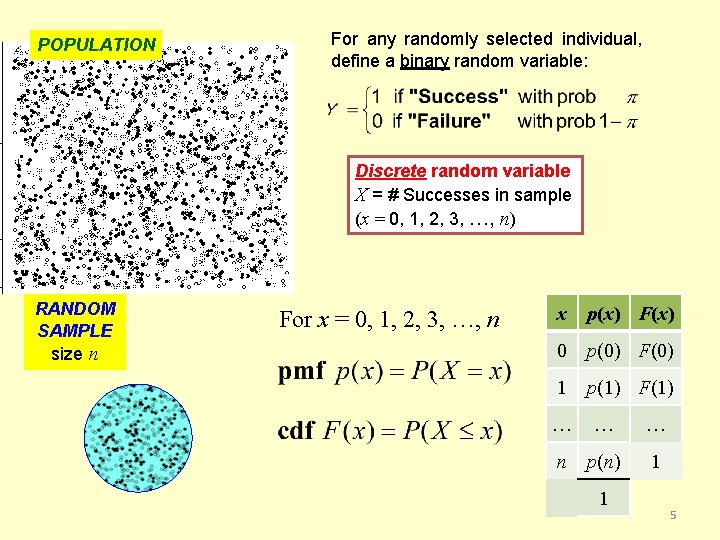
POPULATION For any randomly selected individual, define a binary random variable: Discrete random variable X = # Successes in sample (x = 0, 1, 2, 3, …, n) RANDOM SAMPLE size n For x = 0, 1, 2, 3, …, n x p(x) F(x) 0 p(0) F(0) 1 p(1) F(1) … … … n p(n) 1 1 5

POPULATION For any randomly selected individual, define a binary random variable: Discrete random variable X = # Heads in sample (x = 0, 1, 2, 3, …, n) Reformulate this as n independent coin tosses. RANDOM SAMPLE size n . … etc…. Each such sequence has probability There are x Heads. such sequences of n tosses, with

For any randomly selected individual, define a binary random variable: POPULATION “Success” vs. “Failure” RANDOM SAMPLE of n “Bernoulli trials. ” Discrete random variable X = # Successes in sample (x = 0, 1, 2, 3, …, n) independent, with constant probability ( ) per trial Then X is said to follow a Binomial distribution, written X ~ Bin(n, ), with “probability mass function” p(x) = , x = 0, 1, 2, …, n. 7

Example: Blood Type probabilities, revisited Rh Factor Blood Type + – O . 384 . 077 . 461 A . 323 . 065 . 388 B . 094 . 017 . 111 AB . 032 . 007 . 039 . 833 . 166 . 999 Suppose n = 10 individuals are to be selected at random from the population. Probability table for X = #(Type O) Binomial model applies? Check: 1. Independent outcomes? Reasonably assume that outcomes “Type O” vs. “Not Type O” between two individuals are independent of each other. 2. Constant probability ? From table, = P(Type O) =. 461 throughout population.

Example: Blood Type probabilities, revisited p(x) = R: dbinom(0: 10, . 461) Rh Factor Blood Type + – O . 384 . 077 A . 323 B AB (. 461)x (. 539)10 – x x p(x) F (x) 0 (. 461)0 (. 539)10 = 0. 00207 . 461 1 (. 461)1 (. 539)9 = 0. 01770 0. 01977 . 065 . 388 2 (. 461)2 (. 539)8 = 0. 06813 0. 08790 . 094 . 017 . 111 . 007 . 039 (. 461)3 (. 539)7 = 0. 15538 0. 24328 . 032 3 . 833 . 166 . 999 4 (. 461)4 (. 539)6 = 0. 23257 0. 47585 5 (. 461)5 (. 539)5 = 0. 23870 0. 71455 6 (. 461)6 (. 539)4 = 0. 17013 0. 88468 7 (. 461)7 (. 539)3 = 0. 08315 0. 96783 8 (. 461)8 (. 539)2 = 0. 02667 0. 99450 9 (. 461)9 (. 539)1 = 0. 00507 0. 99957 (. 461)10 (. 539)0 = 0. 00043 1. 00000 Suppose n = 10 individuals are to be selected at random from the population. Probability table for X = #(Type O) Binomial model applies. X ~ Bin(10, . 461) 10 n = 4. 61 = (10)(. 461) Also, can show mean = x p(x) = and variance 2 = (x – ) 2 p(x) = n (1 – ) = 2. 48 1
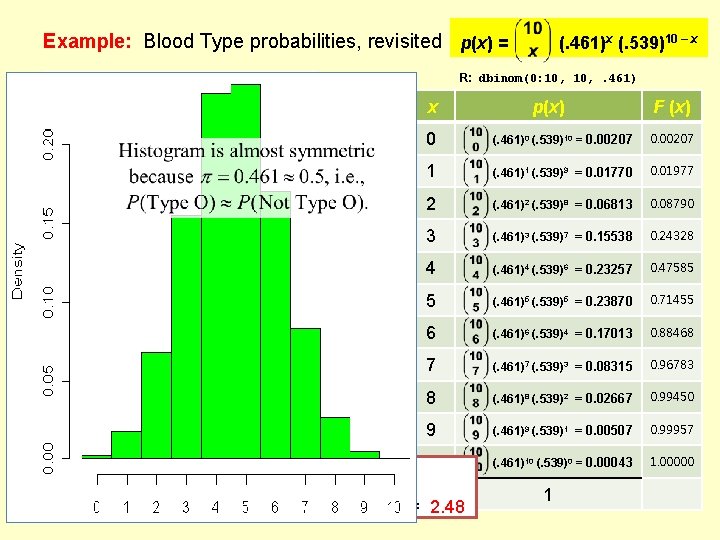
Example: Blood Type probabilities, revisited p(x) = R: dbinom(0: 10, . 461) Rh Factor Blood Type + – O . 384 . 077 A . 323 B AB (. 461)x (. 539)10 – x x p(x) F (x) 0 (. 461)0 (. 539)10 = 0. 00207 . 461 1 (. 461)1 (. 539)9 = 0. 01770 0. 01977 . 065 . 388 2 (. 461)2 (. 539)8 = 0. 06813 0. 08790 . 094 . 017 . 111 . 007 . 039 (. 461)3 (. 539)7 = 0. 15538 0. 24328 . 032 3 . 833 . 166 . 999 4 (. 461)4 (. 539)6 = 0. 23257 0. 47585 5 (. 461)5 (. 539)5 = 0. 23870 0. 71455 6 (. 461)6 (. 539)4 = 0. 17013 0. 88468 7 (. 461)7 (. 539)3 = 0. 08315 0. 96783 8 (. 461)8 (. 539)2 = 0. 02667 0. 99450 9 (. 461)9 (. 539)1 = 0. 00507 0. 99957 10 (. 461)10 (. 539)0 = 0. 00043 1. 00000 Suppose n = 10 individuals are to be selected at random from the population. Probability table for X = #(Type O) Binomial model applies. X ~ Bin(10, . 461) Also, can show mean = x p(x) = n = 4. 61 and variance 2 = (x – ) 2 p(x) = n (1 – ) = 2. 48 1
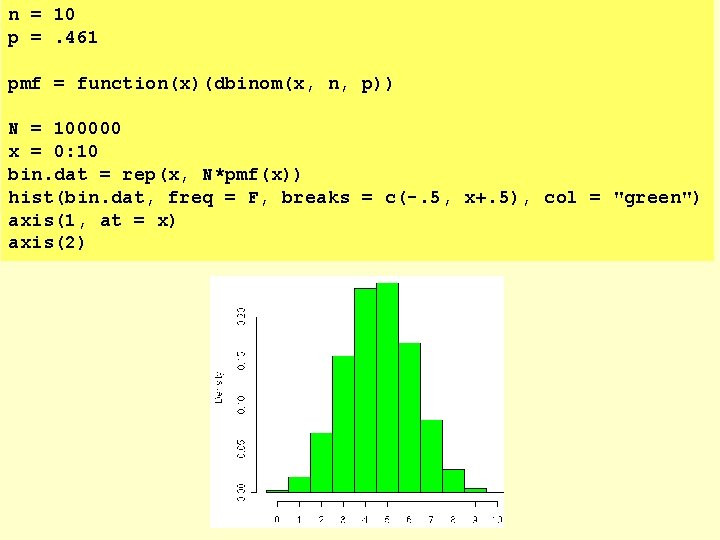
n = 10 p =. 461 pmf = function(x)(dbinom(x, n, p)) N = 100000 x = 0: 10 bin. dat = rep(x, N*pmf(x)) hist(bin. dat, freq = F, breaks = c(-. 5, x+. 5), col = "green") axis(1, at = x) axis(2)

Example: Blood Type probabilities, revisited Rh Factor Blood Type + Therefore, p(x) = – O . 384 . 077 . 461 A . 323 . 065 . 388 B . 094 . 017 . 111 AB . 032 . 007 . 039 . 833 . 166 . 999 1500 individuals Suppose nn==10 individuals areare to to be selected at random from the population. Probability table for X = #(Type AB–) Binomial model applies. X ~ Bin(10, Bin(1500, . 461). 007) Also, can show mean = x p (x) = n = 10. 5 – ) = 10. 43 2. 48 and variance 2 = (x – ) 2 p(x) = n (1 x = 0, 1, 2, …, 1500. RARE EVENT!
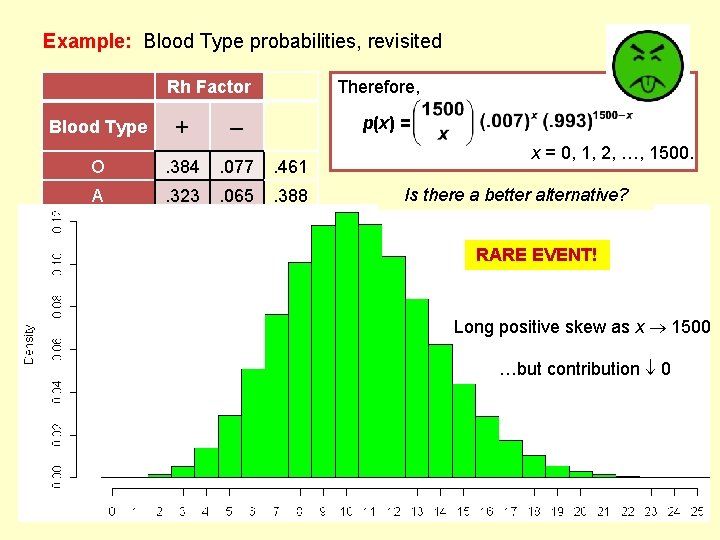
Example: Blood Type probabilities, revisited Rh Factor Blood Type + Therefore, p(x) = – O . 384 . 077 . 461 A . 323 . 065 . 388 B . 094 . 017 . 111 AB . 032 . 007 . 039 . 833 . 166 . 999 x = 0, 1, 2, …, 1500. Is there a better alternative? 1500 individuals Suppose nn==10 individuals areare to to be selected at random from the population. RARE EVENT! Long positive skew as x 1500 Probability table for X = #(Type AB–) Binomial model applies. X ~ Bin(10, Bin(1500, . 461). 007) Also, can show mean = x p (x) = n = 10. 5 – ) = 10. 43 2. 48 and variance 2 = (x – ) 2 p(x) = n (1 …but contribution 0

Example: Blood Type probabilities, revisited Rh Factor Blood Type + Therefore, p(x) = – x = 0, 1, 2, …, 1500. O . 384 . 077 . 461 A . 323 . 065 . 388 B . 094 . 017 . 111 Poisson distribution AB . 032 . 007 . 039 RARE EVENT! . 833 . 166 . 999 individuals Suppose n = 1500 10 individuals areare to to be selected at random from the population. Probability table for X = #(Type AB–) Is there a better alternative? x = 0, 1, 2, …, where mean and variance are = n = 10. 5 and 2 = n = 10. 5 Binomial model applies. X ~ Bin(1500, . 007) Also, can show mean = x p(x) = n = 10. 5 and variance 2 = (x – ) 2 p(x) = n (1 – ) = 10. 43 X ~ Poisson(10. 5) Notation: Sometimes the symbol (“lambda”) is used instead of (“mu”).

Example: Blood Type probabilities, revisited Rh Factor Blood Type + Therefore, p(x) = – x = 0, 1, 2, …, 1500. O . 384 . 077 . 461 A . 323 . 065 . 388 B . 094 . 017 . 111 Poisson distribution AB . 032 . 007 . 039 RARE EVENT! . 833 . 166 . 999 Is there a better alternative? Suppose n = 1500 individuals are to be selected at random from the population. Probability table for X = #(Type AB–) x = 0, 1, 2, …, where mean and variance are = n = 10. 5 and 2 = n = 10. 5 Ex: Probability of exactly X = 15 Type(AB–) individuals = ? Binomial: Poisson: X ~ Poisson(10. 5) (both ≈. 0437)
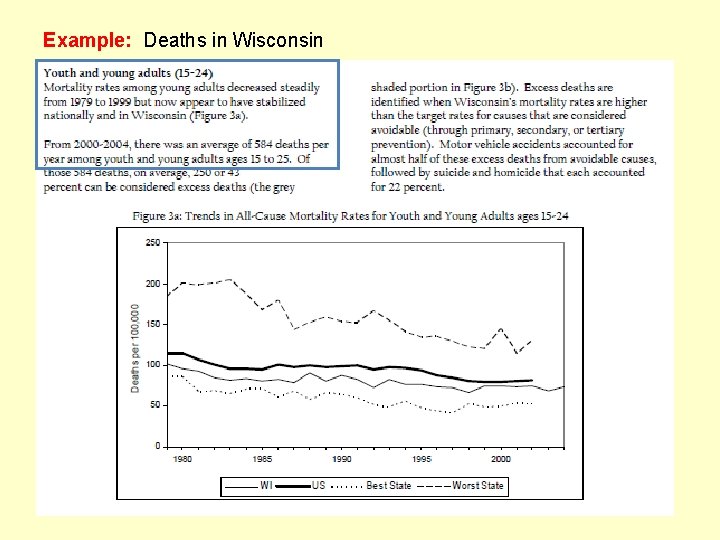
Example: Deaths in Wisconsin

Example: Deaths in Wisconsin Assuming deaths among young adults are relatively rare, we know the following: • Average λ = 584 deaths per year • Mortality rate (α) seems constant. Therefore, the Poisson distribution can be used as a good model to make future predictions about the random variable X = “# deaths” per year, for this population (15 -24 yrs)… assuming current values will still apply. Probability of exactly X = 600 deaths next year P(X = 600) = Probability of exactly X = 1200 deaths in the next two years Mean of 584 deaths per yr Mean of 1168 deaths per two yrs, so let λ = 1168: P(X = 1200) = R: dpois(600, 584) 0. 0131 0. 00746 Probability of at least one death per day: λ = P(X ≥ 1) = P(X = 1) + P(X = 2) + P(X = 3) + … P(X ≥ 1) = 1 – P(X = 0) = 1 – = 1. 6 deaths/day True, but not practical. = 1 – e– 1. 6 = 0. 798
- Slides: 17