Chapter 3 CT LTI Systems Updated 91613 A

Chapter 3 CT LTI Systems Updated: 9/16/13

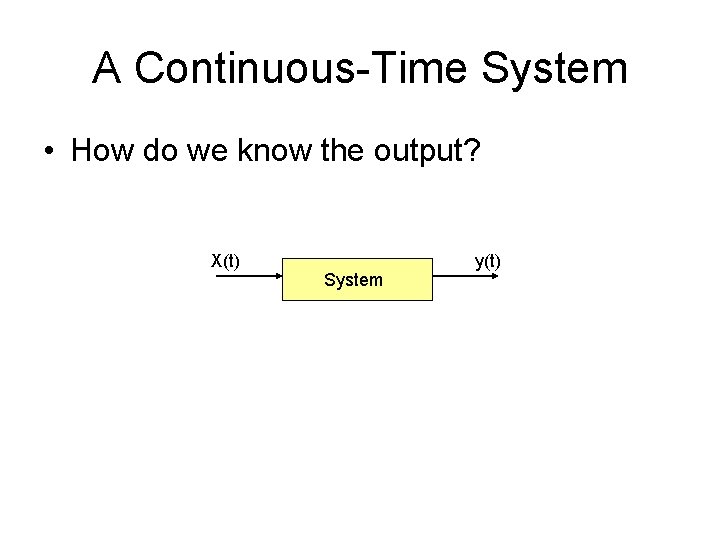
A Continuous-Time System • How do we know the output? X(t) System y(t)

LTI Systems • Time Invariant – X(t) y(t) & x(t-to) y(t-to) • Linearity – a 1 x 1(t)+ a 2 x 2(t) a 1 y 1(t)+ a 2 y 2(t) – a 1 y 1(t)+ a 2 y 2(t)= T[a 1 x 1(t)+a 2 x 2(t)] • Meet the description of many physical systems • They can be modeled systematically – Non-LTI systems typically have no general mathematical procedure to obtain solution What is the input-output relationship for LTI-CT Systems?

Convolution Integral • An approach (available tool or operation) to describe the input-output relationship for LTI Systems X(t)=d(t) • In a LTI system LTI System y(t)=h(t) – d(t) h(t) – Remember h(t) is T[d(t)] – Unit impulse function the impulse response • It is possible to use h(t) to solve for any input-output relationship X(t) LTI System: h(t) y(t) • One way to do it is by using the Convolution Integral

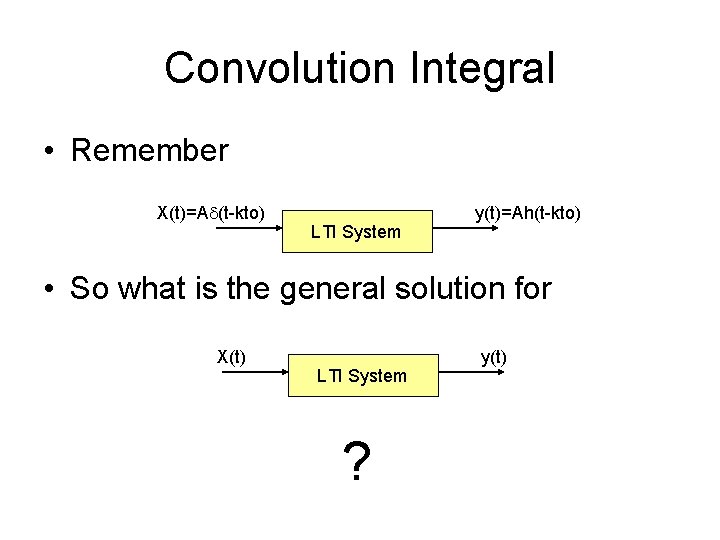
Convolution Integral • Remember X(t)=Ad(t-kto) LTI System y(t)=Ah(t-kto) • So what is the general solution for X(t) LTI System ? y(t)

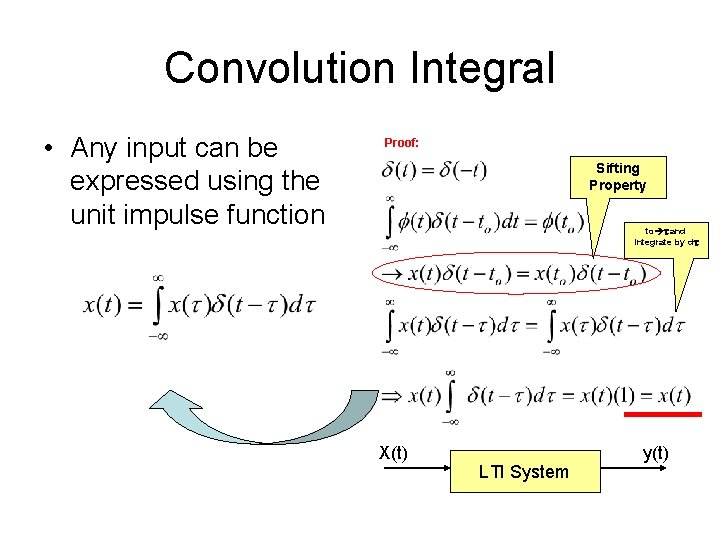
Convolution Integral • Any input can be expressed using the unit impulse function Proof: Sifting Property to t and integrate by dt X(t) LTI System y(t)

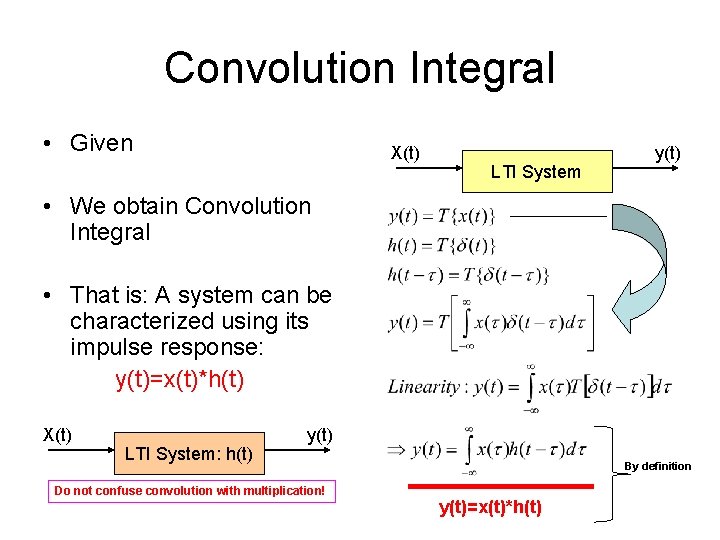
Convolution Integral • Given X(t) LTI System y(t) • We obtain Convolution Integral • That is: A system can be characterized using its impulse response: y(t)=x(t)*h(t) X(t) LTI System: h(t) y(t) Do not confuse convolution with multiplication! By definition y(t)=x(t)*h(t)

Convolution Integral X(t) LTI System: h(t) y(t)

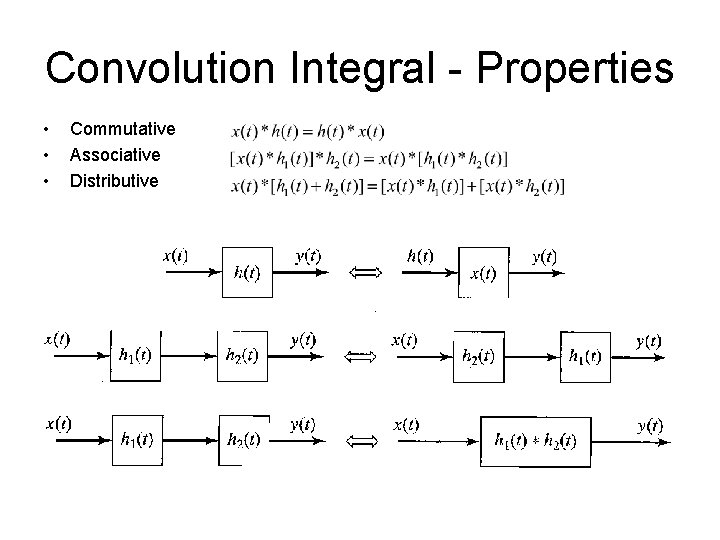
Convolution Integral - Properties • Commutative • Associative • Distributive • Thus, using commutative property: Next: We draw the block diagram representation!

Convolution Integral - Properties • • • Commutative Associative Distributive

Simple Example • What if a step unit function is the input of a LTI system? u(t) LTI System y(t)=S{u(t)}=s(t) • S(t) is called the Step Response Step response can be obtained by integrating the impulse response! Impulse response can be obtained by differentiating the step response

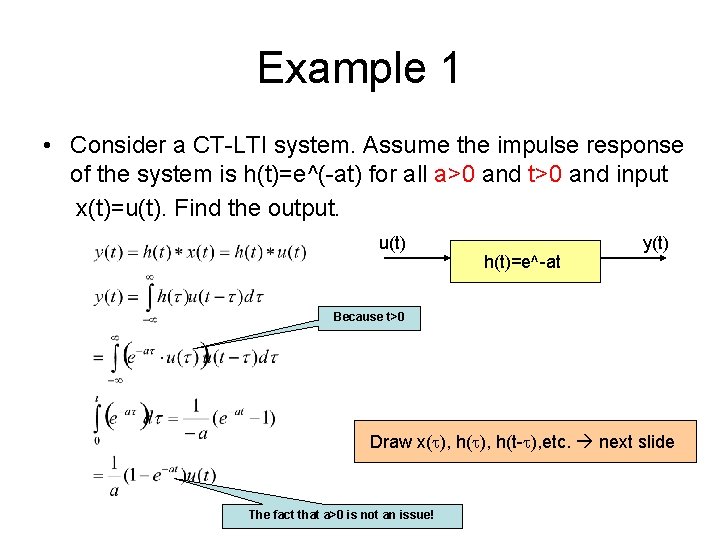
Example 1 • Consider a CT-LTI system. Assume the impulse response of the system is h(t)=e^(-at) for all a>0 and t>0 and input x(t)=u(t). Find the output. u(t) h(t)=e^-at y(t) Because t>0 Draw x(t), h(t-t), etc. next slide The fact that a>0 is not an issue!

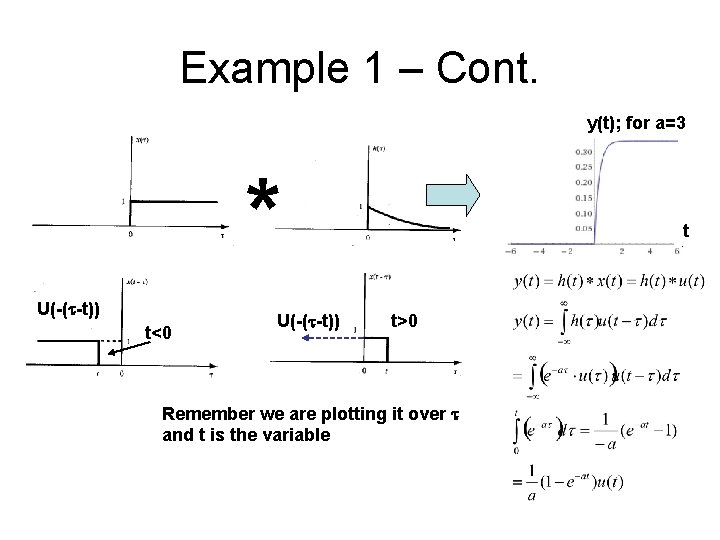
Example 1 – Cont. y(t); for a=3 y(t) * U(-(t-t)) t<0 U(-(t-t)) t t t>0 Remember we are plotting it over t and t is the variable

Example 1 – Cont. Graphical Representation (similar) a=1 In this case! http: //www. wolframalpha. com/input/? i=convolution+of+two+functions&lk=4&num=4

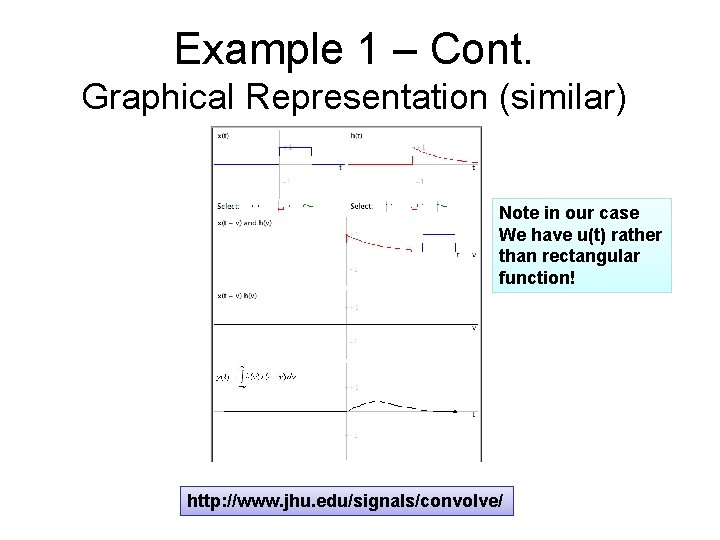
Example 1 – Cont. Graphical Representation (similar) Note in our case We have u(t) rather than rectangular function! http: //www. jhu. edu/signals/convolve/

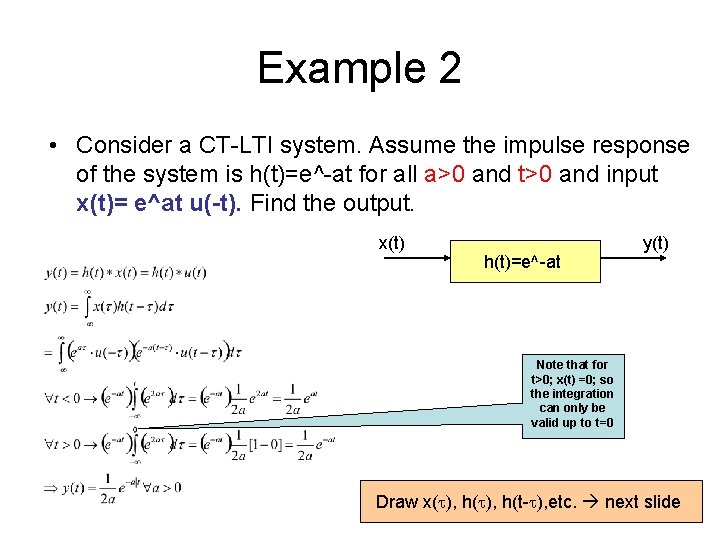
Example 2 • Consider a CT-LTI system. Assume the impulse response of the system is h(t)=e^-at for all a>0 and t>0 and input x(t)= e^at u(-t). Find the output. x(t) h(t)=e^-at y(t) Note that for t>0; x(t) =0; so the integration can only be valid up to t=0 Draw x(t), h(t-t), etc. next slide

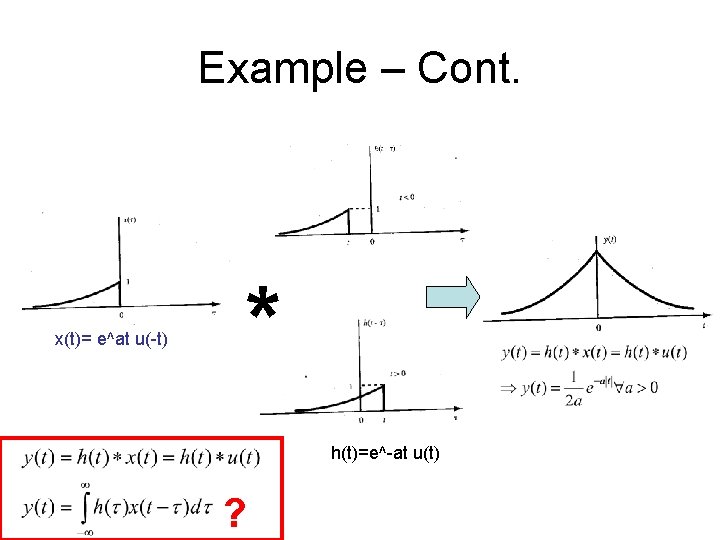
Example – Cont. x(t)= e^at u(-t) * h(t)=e^-at u(t) ?

Another Example notes

Properties of CT LTI Systems • When is a CT LTI system memory-less (static) • When does a CT LTI system have an inverse system (invertible)? • When is a CT LTI system considered to be causal? Assuming the input is causal: • When is a CT LTI system considered to be Stable? notes

Example • Is this an stable system? • What about this? notes

Differential-Equations Models • This is a linear first order differential equation with constant coefficients (assuming a and b are constants) • The general nth order linear DE with constant equations is

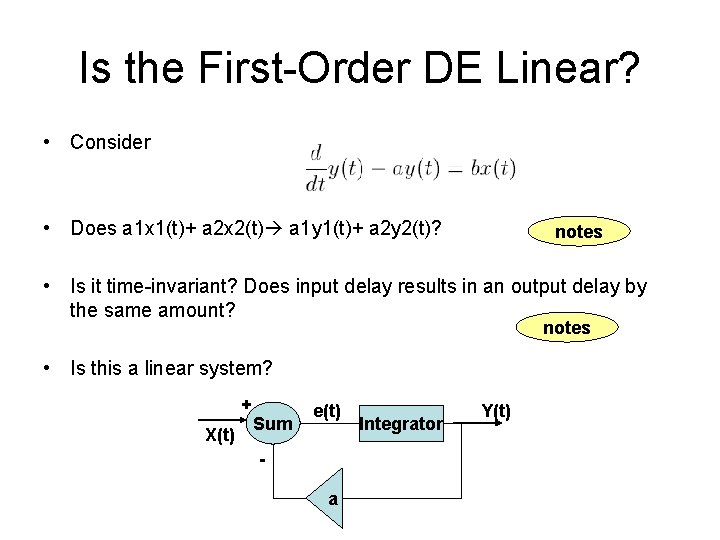
Is the First-Order DE Linear? • Consider • Does a 1 x 1(t)+ a 2 x 2(t) a 1 y 1(t)+ a 2 y 2(t)? notes • Is it time-invariant? Does input delay results in an output delay by the same amount? notes • Is this a linear system? + X(t) Sum e(t) a Integrator Y(t)

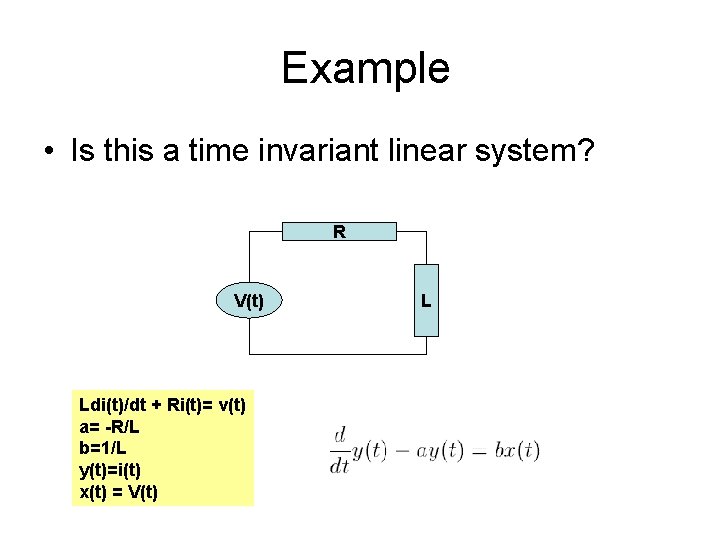
Example • Is this a time invariant linear system? R V(t) Ldi(t)/dt + Ri(t)= v(t) a= -R/L b=1/L y(t)=i(t) x(t) = V(t) L

Solution of DE • A classical model for the solution of DE is called method of undermined coefficients – yc(t) is called the complementary or natural solution – yp(t) is called the particular or forced solution

Solution of DE Thus, for x(t) =constant yp(t)=P x(t) =Ce^-7 t yp(t)= Pe^-7 t x(t) =2 cos(3 t) yp(t)=P 1 cos(3 t)+P 2 sin(3 t)

Example • Solve – Assume x(t) = 2 and y(0) = 4 yc(t) = Ce^-2 t; yp(t) = P; P = 1 y(t) = Ce^-2 t + 1 y(0) = 4 C = 3 y(t) = 3 e^-2 t + 1 – What happens if notes

Schaum’s Examples • Chapter 2: – 2, 4 -6, 8, 10, 11 -14, 18, 19, 48, 52, 53,