Chapter 3 Complex Numbers Quadratic Functions and Equations

Chapter 3 • • • Complex Numbers Quadratic Functions and Equations Inequalities Rational Equations Radical Equations Absolute Value Equations

Willa Cather –U. S. novelist • “Art, it seems to me, should simplify. That indeed, is very nearly the whole of the higher artistic process; finding what conventions of form and what detail one can do without and yet preserve the spirit of the whole – so that all one has suppressed and cut away is there to the reader’s consciousness as much as if it were in type on the page.

Mathematics 116 • Complex Numbers

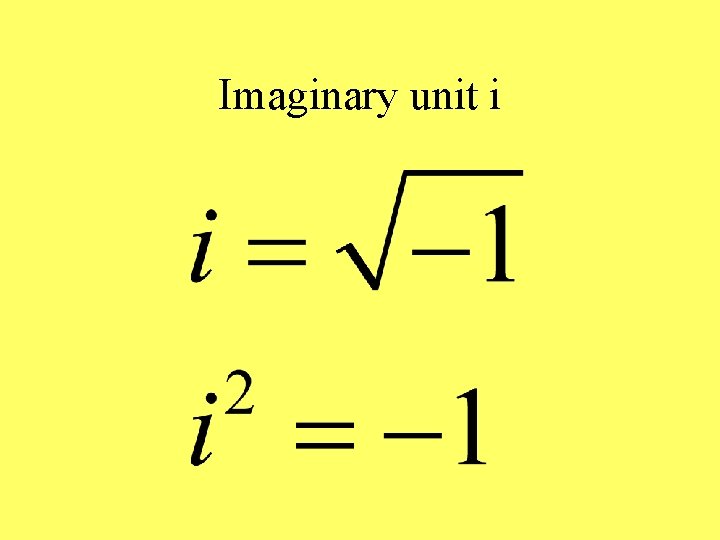
Imaginary unit i

Set of Complex Numbers • R = real numbers • I = imaginary numbers • C = Complex numbers

Elbert Hubbard –“Positive anything is better than negative nothing. ”

Standard Form of Complex number • a + bi • Where a and b are real numbers • 0 + bi = bi is a pure imaginary number

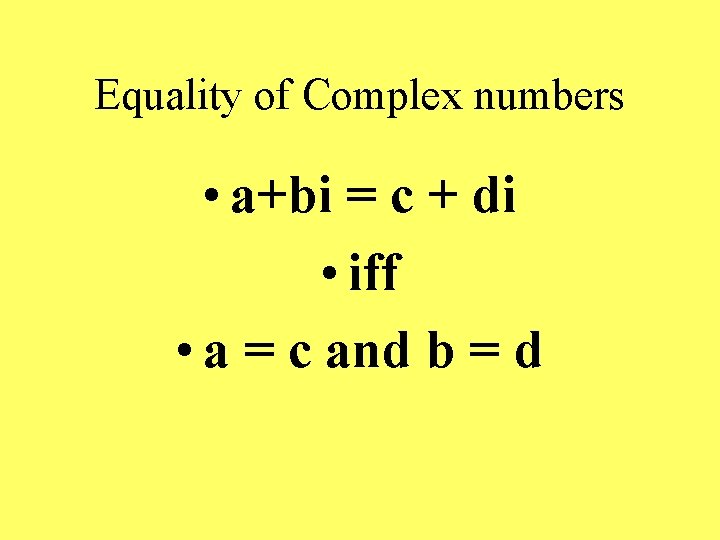
Equality of Complex numbers • a+bi = c + di • iff • a = c and b = d

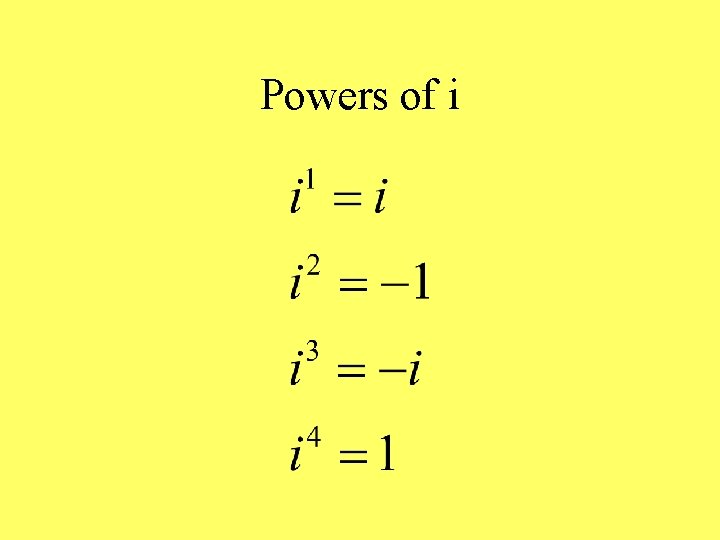
Powers of i

Add and subtract complex #s • Add or subtract the real and imaginary parts of the numbers separately.

Orison Swett Marden • “All who have accomplished great things have had a great aim, have fixed their gaze on a goal which was high, one which sometimes seemed impossible. ”

Multiply Complex #s • Multiply as if two polynomials and combine like terms as in the FOIL • Note i squared = -1

Complex Conjugates • a – bi is the conjugate of a + bi • The product is a rational number

Divide Complex #s • Multiply numerator and denominator by complex conjugate of denominator. • Write answer in standard form

Harry Truman – American President • “A pessimist is one who makes difficulties of his opportunities and an optimist is one who makes opportunities of his difficulties. ”

Calculator and Complex #s • Use Mode – Complex • Use i second function of decimal point • Use [Math] [Frac] and place in standard form a + bi • Can add, subtract, multiply, and divide complex numbers with calculator.

Mathematics 116 • Solving Quadratic Equations • Algebraically • This section contains much information

Def: Quadratic Function • General Form • a, b, c, are real numbers and a not equal 0

Objective – Solve quadratic equations • • Two distinct solutions One Solution – double root Two complex solutions Solve for exact and decimal approximations

Solving Quadratic Equation #1 • Factoring • • • Use zero Factor Theorem Set = to 0 and factor Set each factor equal to zero Solve Check

Solving Quadratic Equation #2 • Graphing • Solve for y • Graph and look for x intercepts • Can not give exact answers • Can not do complex roots.

Solving Quadratic Equations #3 Square Root Property • For any real number c

Sample problem

Sample problem 2

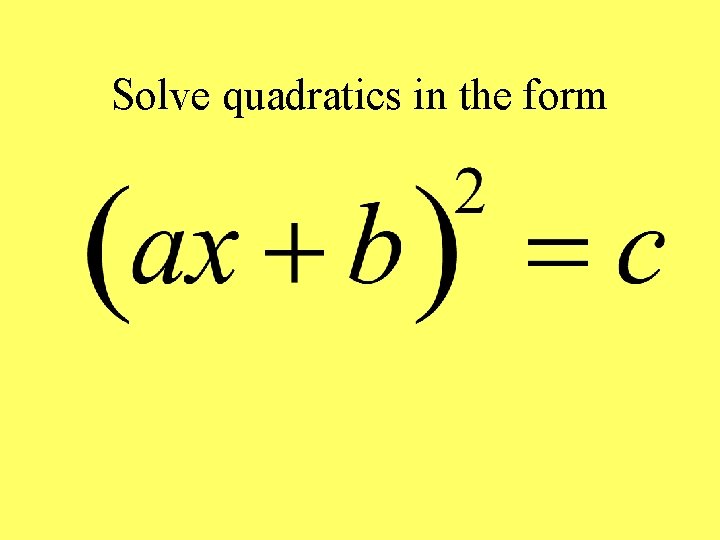
Solve quadratics in the form

Procedure • • • 1. Use LCD and remove fractions 2. Isolate the squared term 3. Use the square root property 4. Determine two roots 5. Simplify if needed

Sample problem 3

Sample problem 4

Dorothy Broude • “Act as if it were impossible to fail. ”

Completing the square informal • Make one side of the equation a perfect square and the other side a constant. • Then solve by methods previously used.

Procedure: Completing the Square • 1. If necessary, divide so leading coefficient of squared variable is 1. • 2. Write equation in form • 3. Complete the square by adding the square of half of the linear coefficient to both sides. • 4. Use square root property • 5. Simplify

Sample Problem

Sample Problem complete the square 2

Sample problem complete the square #3

Objective: • Solve quadratic equations using the technique of completing the square.

Mary Kay Ash • “Aerodynamically, the bumble bee shouldn’t be able to fly, but the bumble bee doesn’t know it so it goes flying anyway. ”

College Algebra Very Important Concept!!! • The • Quadratic • Formula

Objective of “A” students • Derive • the • Quadratic Formula.

Quadratic Formula • For all a, b, and c that are real numbers and a is not equal to zero

Sample problem quadratic formula #1

Sample problem quadratic formula #2

Sample problem quadratic formula #3

Pearl S. Buck • “All things are possible until they are proved impossible and even the impossible may only be so, as of now. ”

Methods for solving quadratic equations. • 1. • 2. • 3. • 4. Factoring Square Root Principle Completing the Square Quadratic Formula

Discriminant • Negative – complex conjugates • Zero – one rational solution (double root) • Positive – Perfect square – 2 rational solutions – Not perfect square – 2 irrational solutions

Joseph De Maistre (1753 -1821 – French Philosopher • “It is one of man’s curious idiosyncrasies to create difficulties for the pleasure of resolving them. ”

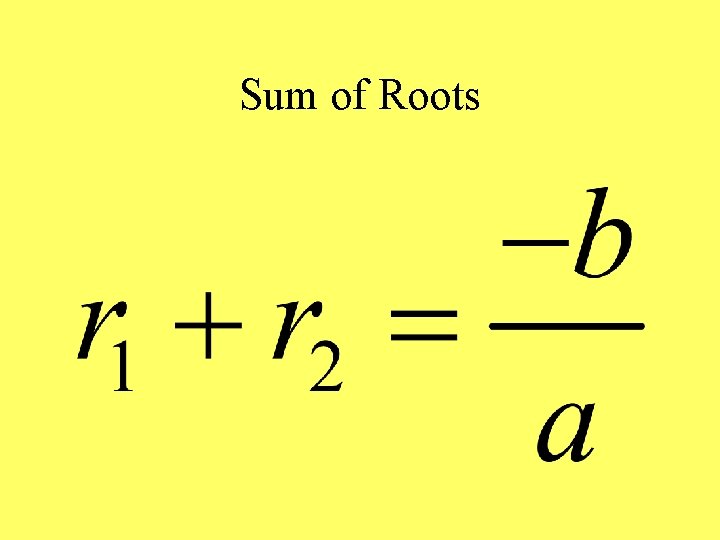
Sum of Roots

Product of Roots

Calculator Programs • ALGEBRA QUADRATIC • QUADB • ALG 2 • QUADRATIC

Ron Jaworski • “Positive thinking is the key to success in business, education, pro football, anything that you can mention. I go out there thinking that I’m going to complete every pass. ”

Objective • Solve by Extracting Square Roots

Objective: Know and Prove the Quadratic Formula If a, b, c are real numbers and not equal to 0

Objective – Solve quadratic equations • • Two distinct solutions One Solution – double root Two complex solutions Solve for exact and decimal approximations

Objective: Solve Quadratic Equations using Calculator • Graphically • Numerically • Programs – ALGEBRAA – QUADB – ALG 2 – others

Objective: Use quadratic equations to model and solve applied, real-life problems.

D’Alembert – French Mathematician – “The difficulties you meet will resolve themselves as you advance. Proceed, and light will dawn, and shine with increasing clearness on your path. ”

Vertex • The point on a parabola that represents the absolute minimum or absolute maximum – otherwise known as the turning point. • y coordinate determines the range. • (x, y)

Axis of symmetry • The vertical line that goes through the vertex of the parabola. • Equation is x = constant

Objective • Graph, determine domain, range, y intercept, x intercept

Parabola with vertex (h, k) • Standard Form

Standard Form of a Quadratic Function • • • Graph is a parabola Axis is the vertical line x = h Vertex is (h, k) a>0 graph opens upward a<0 graph opens downward

Find Vertex • x coordinate is • y coordinate is

Vertex of quadratic function

Objective: Find minimum and maximum values of functions in real life applications. • 1. Graphically • 2. Algebraically – Standard form – Use vertex 3. Numerically

Roger Maris, New York Yankees Outfielder • “You hit home runs not by chance but by preparation. ”

Objective: • Solve Rational Equations –Check for extraneous roots –Graphically and algebraically

Objective • Solve equations involving radicals –Solve Radical Equations Check for extraneous roots –Graphically and algebraically

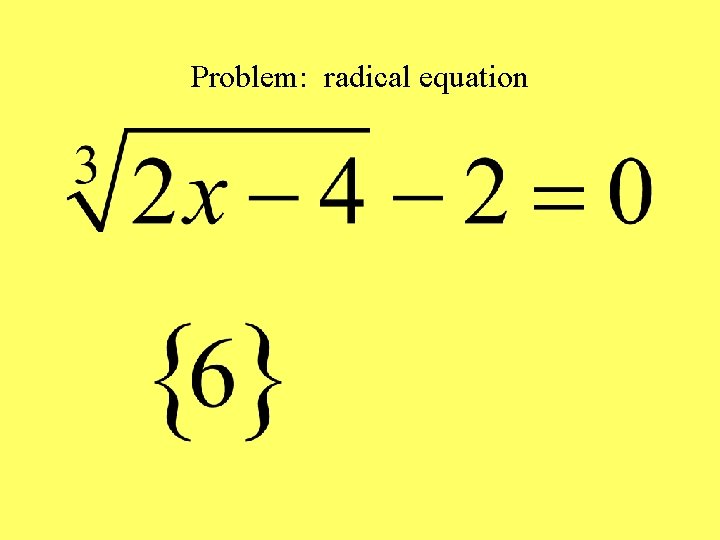
Problem: radical equation

Problem: radical equation

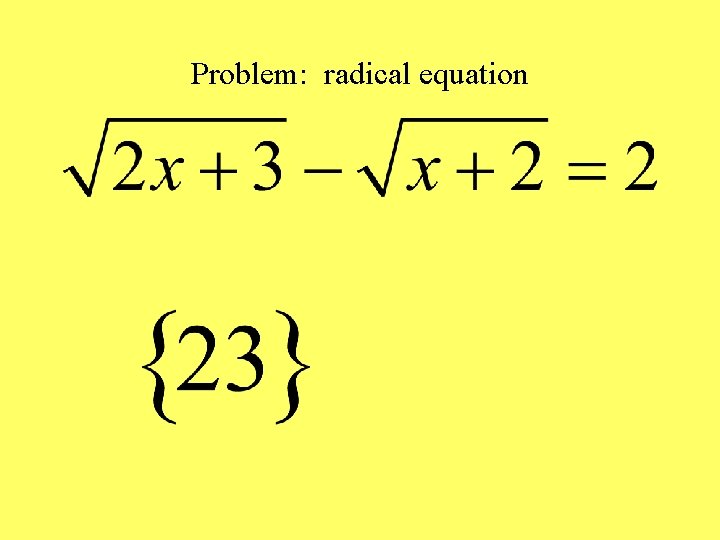
Problem: radical equation

Objective: • Solve Equations • Quadratic in Form

Objective • Solve equations • involving • Absolute Value

Procedure: Absolute Value equations • 1. Isolate the absolute value • 2. Set up two equations joined by “or”and so note • 3. Solve both equations • 4. Check solutions

Elbert Hubbard • “Positive anything is better than negative nothing. ”

Elbert Hubbard • “Positive anything is better than negative nothing. ”

Addition Property of Inequality • Addition of a constant • If a < b then a + c < b + c

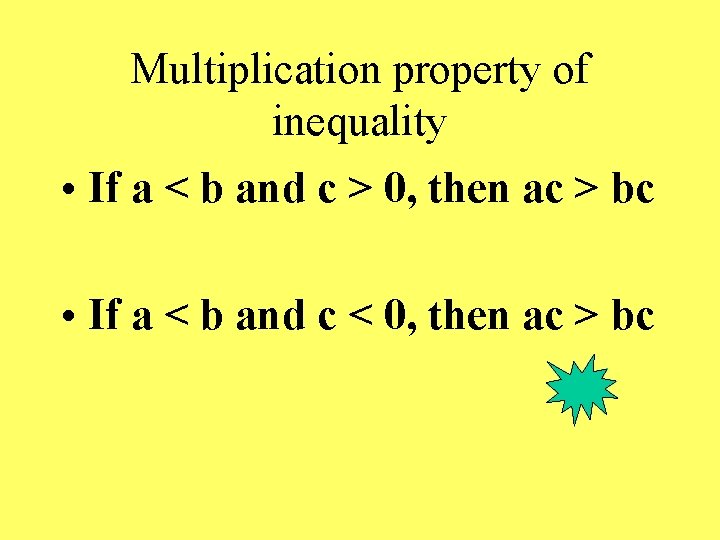
Multiplication property of inequality • If a < b and c > 0, then ac > bc • If a < b and c < 0, then ac > bc

Objective: • Solve Inequalities Involving Absolute Value. • Remember < uses “AND” • Remember > uses “OR” • and/or need to be noted

Objective: Estimate solutions of inequalities graphically. • Two Ways – Change inequality to = and set = to 0 – Graph in 2 -space – Or Use Test and Y= with appropriate window

Objective: • Solve Polynomial Inequalities –Graphically –Algebraically –(graphical is better the larger the degree)

Objectives: • Solve Rational Inequalities –Graphically –algebraically • Solve models with inequalities

Zig Ziglar • “Positive thinking won’t let you do anything but it will let you do everything better than negative thinking will. ”

Zig Ziglar • “Positive thinking won’t let you do anything but it will let you do everything better than negative thinking will. ”

Mathematics 116 Regression Continued • Explore data: Quadratic Models and Scatter Plots

Objectives • Construct Scatter Plots – By hand – With Calculator • Interpret correlation – Positive – Negative – No discernible correlation

Objectives: • Use the calculator to determine quadratic models for data. • Graph quadratic model and scatter plot • Make predictions based on model

Napoleon Hill • “There are no limitations to the mind except those we acknowledge. ”