Chapter 3 Block Ciphers and the Advanced Encryption

Chapter 3 Block Ciphers and the Advanced Encryption Standard 1

Outline n n n n 3. 1 3. 2 3. 3 3. 4 3. 5 3. 6 3. 7 Introduction Substitution-Permutation Networks Linear cryptanalysis Differential cryptanalysis The Data Encryption Standard The Advanced Encryption Standard Modes of Operation 2

3. 5 The Data Encryption Standard n n n DES was developed at IBM, as a modification of an earlier system known as Lucifer. DES was first published in the Federal Register of March 17, 1975. DES was adopted as a standard for “unclassified” applications on January 15, 1977. 3

The Data Encryption Standard n 3. 5. 1 Description of DES n DES is a special type of iterated cipher called a Feistel cipher. n In a Feistel cipher, each state ui is divided into two halves of equal length, say Li and Ri. Round function g: g(Li-1, Ri-1, Ki)=(Li, Ri), where n Invertible: n 4
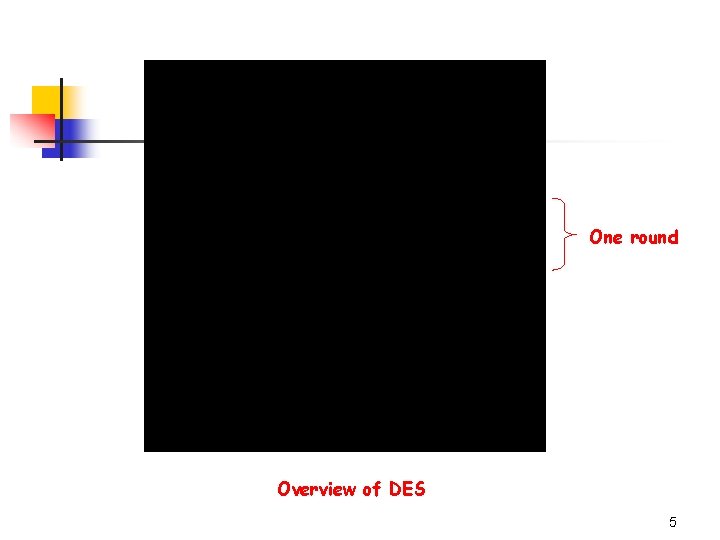
One round Overview of DES 5

The Data Encryption Standard n n Initial permutation IP: IP(x)=L 0 R 0 Inverse permutation IP-1: y=IP-1(R 16 L 16) n n Note L 16 and R 16 are swapped before IP-1 is applied. Each Li and Ri is 32 bits in length. The function takes as input a 32 -bit string (the right half of the current state) and a round key. Key schedule (K 1, K 2, …, K 16) consists of 48 -bit round keys that are derived from the 56 -bit key, K. 6

The Data Encryption Standard n Suppose we denote the first argument of f function (Figure 3. 7) by A, and the second argument by J. n n A is expanded to 48 -bit according to a fixed expansion function E. Compute and write the result as concatenation of eight 6 -bit strings B=B 1 B 2 B 3 B 4 B 5 B 6 B 7 B 8. The next step uses eight S-boxes (S 1, …, S 8), Given a bitstring of length 6, Bj=b 1 b 2 b 3 b 4 b 5 b 6. b 1 b 6 determine the row r of Sj, and b 2 b 3 b 4 b 5 determine the column c of Sj. We compute Cj=Sj(Bj). The bitstring C=C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 is permuted according to the permutation P. Then f (A, J)=P(C). 7
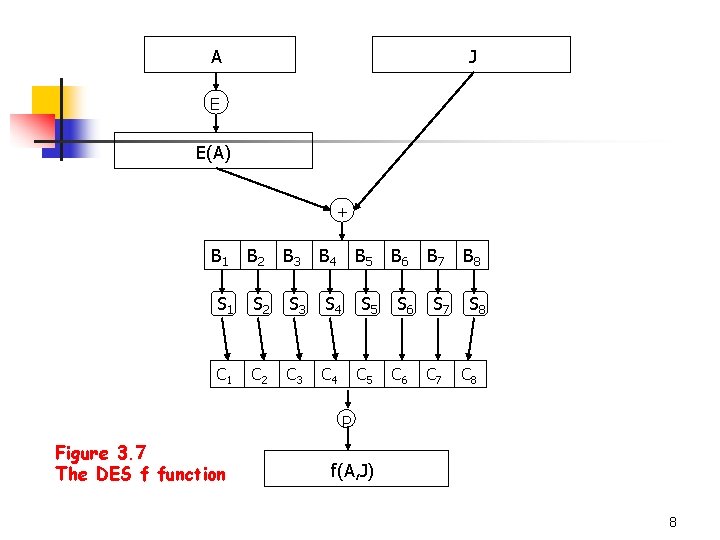
A J E E(A) + B 1 B 2 B 3 B 4 B 5 S 1 S 2 S 3 S 4 S 5 C 1 C 2 C 3 C 4 C 5 B 6 S 6 C 6 B 7 S 7 C 7 B 8 S 8 C 8 P Figure 3. 7 The DES f function f(A, J) 8
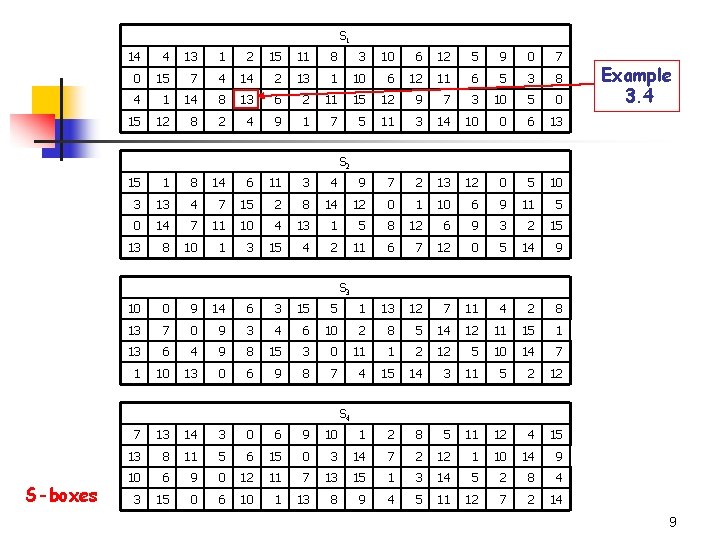
S 1 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 0 15 7 4 14 2 13 1 10 6 12 11 6 5 3 8 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13 Example 3. 4 S 2 15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9 S 3 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8 13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12 S 4 S-boxes 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15 13 8 11 5 6 15 0 3 14 7 2 12 1 10 14 9 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4 3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14 9
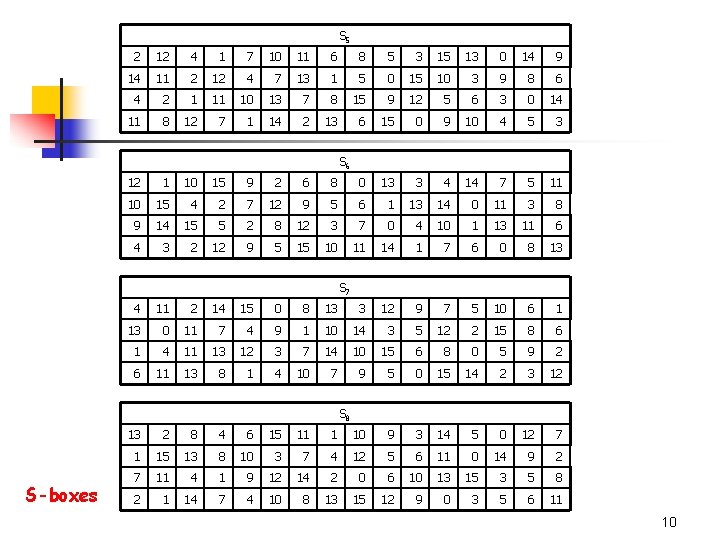
S 5 2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6 4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14 11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3 S 6 12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11 10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13 S 7 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12 S 8 S-boxes 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11 10

The Data Encryption Standard n Example 3. 4: We show to compute an output of S-box S 1 with input 101000. n n n b 1 b 6=10 which is 2 b 2 b 3 b 4 b 5=1000 which is 4 Output is row 2 and column 4 of S 1. n n Note: rows are numbered 0, 1, 2, 3 and columns are 0, 1, 2, … 15 So the output is 13 which is 1101 in binary. 11

The Data Encryption Standard n n The expansion function E is specified by the following table: E bit-selection table 32 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 1 If A=(a 1, a 2, …, a 32) then E(A)=(a 32, a 1, a 2, a 3, a 4, a 5, a 4, …, a 31, a 32, a 1). 12

The Data Encryption Standard n The permutation P is as follows: P n 16 7 20 21 29 12 28 17 1 15 23 26 5 18 31 10 2 8 24 14 32 27 3 9 19 13 30 6 22 11 4 25 If C=(c 1, c 2, …, c 32) then P(C)=(c 16, c 7, c 20, c 21, c 29, …, c 11, c 4, c 25). 13
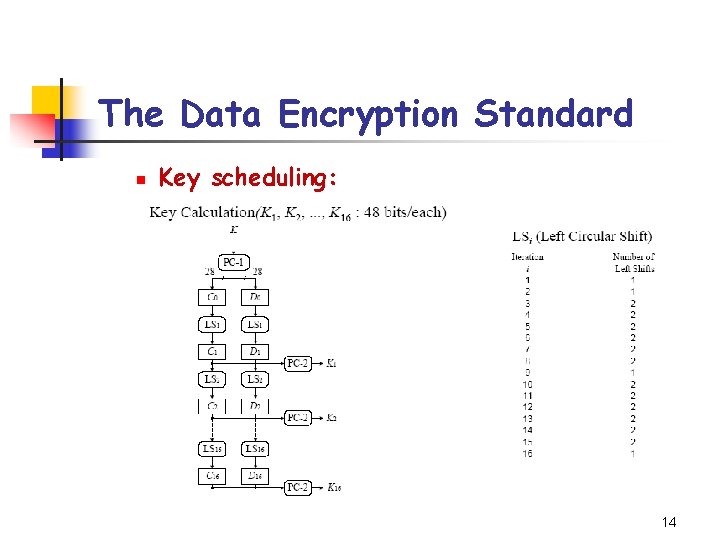
The Data Encryption Standard n Key scheduling: 14

The Data Encryption Standard 15

The Data Encryption Standard n 3. 5. 2: Analysis of DES n n The S-boxes, being the non-linear components of the cryptosystem, are vital to its security. DES was to make differential cryptanalysis infeasible. n n Differential cryptanalysis was known to IBM when they design DES, but it was kept secret for almost 20 years until Biham and Shamir invented the technique in the early 1990’s. The most pertinent criticism of DES is that the size of the keyspace, 256, is too small. 16

The Data Encryption Standard n Many people try to design a special purpose machine to do exhaustive key search. n n Ex: “DES Cracker” contained 1536 chips and could search 88 billion keys per second. It won RSA Laboratory’s “DES Challenge II-2” by successfully finding a DES key in 56 hours. Other than exhaustive key search, differential cryptanalysis and linear cryptanalysis are the most important attacks. (linear attack is more efficient) n n In 1994, Matsui implemented the attack by using 243 plaintextciphertext pairs with the same key. It took 40 days to generate the pairs and 10 days to find the key. DES is still secure theoretically due to the extremely large number of pairs required. An adversary is impossible to collect that amount of pairs. 17

3. 6 The Advanced Encryption Standard n n n On January 2, 1997, NIST began the process of choosing a replacement for DES and called the Advanced Encryption Standard, or AES. It was required that the AES have a block length of 128 bits, and supported key lengths of 128, 192, and 256 bits. After several AES candidate conferences were held. On Oct. 2, 2000, Rijndael was selected. n 3 main criteria: security, cost, algorithm and implementation characteristics 18

The Advanced Encryption Standard n 3. 6. 1 Description of AES n Block length: n n Key length: n n 128 bits (Nb=4) 192 bits (Nb=6) 256 bits (Nb=8) S 0, 0 S 0, 1 S 0, 2 S 0, 3 S 0, 4 S 0, 5 S 0, 6 S 0, 7 S 1, 0 S 1, 1 S 1, 2 S 1, 3 S 1, 4 S 1, 5 S 1, 6 S 1, 7 S 2, 0 S 2, 1 S 2, 2 S 2, 3 S 2, 4 S 2, 5 S 2, 6 S 2, 7 S 3, 0 S 3, 1 S 3, 2 S 3, 3 S 3, 4 S 3, 5 S 3, 6 S 3, 7 128 bits (Nk=4) 192 bits (Nk=6) 256 bits (Nk=8) Number of rounds Nr: 19

The Advanced Encryption Standard n Overview of AES: n ADDROUNDKEY, which xors the Round. Key with State. For each of the first Nr-1 rounds: perform SUBBYTES(State), SHIFTROWS(State), MIXCOLUMN(State), ADDROUNDKEY. n Final round: SUBBYTES, SHIFTROWS, ADDROUNDKEY. n n All operations in AES are byte-oriented. n n The plaintext x consists of 16 byte, x 0, x 1, …, x 15. Initially State is plaintext x (for 128 -bit case): S 0, 0 S 0, 1 S 0, 2 S 0, 3 x 0 x 4 x 8 x 12 S 1, 0 S 1, 1 S 1, 2 S 1, 3 x 1 x 5 x 9 x 13 S 2, 0 S 2, 1 S 2, 2 S 2, 3 x 2 x 6 x 10 x 14 S 3, 0 S 3, 1 S 3, 2 S 3, 3 x 7 x 11 x 15 20
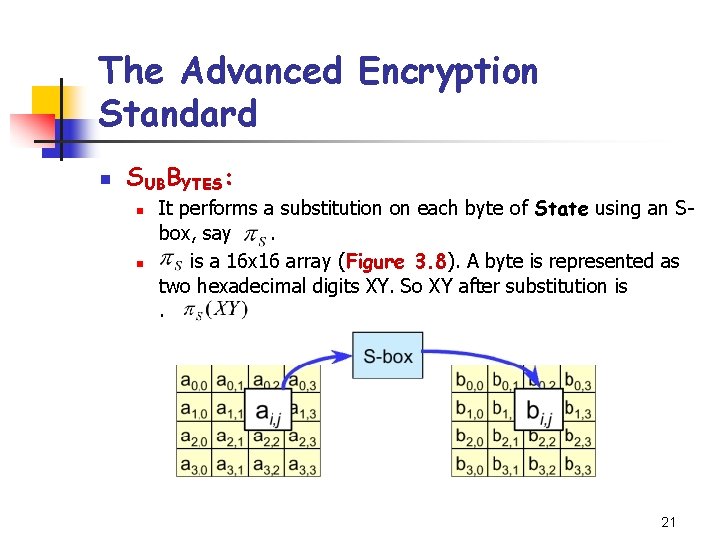
The Advanced Encryption Standard n SUBBYTES: n n It performs a substitution on each byte of State using an Sbox, say. is a 16 x 16 array (Figure 3. 8). A byte is represented as two hexadecimal digits XY. So XY after substitution is. 21
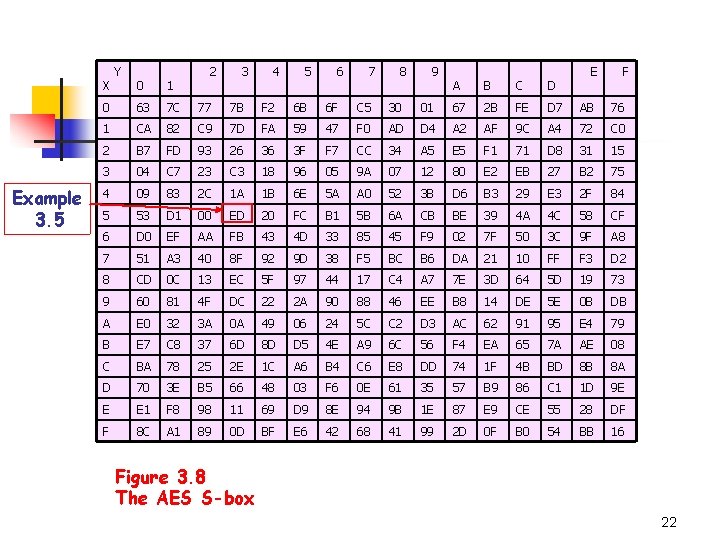
X Example 3. 5 Y 2 3 4 5 6 7 8 0 1 0 63 7 C 77 7 B F 2 6 B 6 F C 5 30 1 CA 82 C 9 7 D FA 59 47 F 0 2 B 7 FD 93 26 36 3 F F 7 3 04 C 7 23 C 3 18 96 4 09 83 2 C 1 A 1 B 5 53 D 1 00 ED 6 D 0 EF AA 7 51 A 3 8 CD 9 9 E F A B C D 01 67 2 B FE D 7 AB 76 AD D 4 A 2 AF 9 C A 4 72 C 0 CC 34 A 5 E 5 F 1 71 D 8 31 15 05 9 A 07 12 80 E 2 EB 27 B 2 75 6 E 5 A A 0 52 3 B D 6 B 3 29 E 3 2 F 84 20 FC B 1 5 B 6 A CB BE 39 4 A 4 C 58 CF FB 43 4 D 33 85 45 F 9 02 7 F 50 3 C 9 F A 8 40 8 F 92 9 D 38 F 5 BC B 6 DA 21 10 FF F 3 D 2 0 C 13 EC 5 F 97 44 17 C 4 A 7 7 E 3 D 64 5 D 19 73 60 81 4 F DC 22 2 A 90 88 46 EE B 8 14 DE 5 E 0 B DB A E 0 32 3 A 0 A 49 06 24 5 C C 2 D 3 AC 62 91 95 E 4 79 B E 7 C 8 37 6 D 8 D D 5 4 E A 9 6 C 56 F 4 EA 65 7 A AE 08 C BA 78 25 2 E 1 C A 6 B 4 C 6 E 8 DD 74 1 F 4 B BD 8 B 8 A D 70 3 E B 5 66 48 03 F 6 0 E 61 35 57 B 9 86 C 1 1 D 9 E E E 1 F 8 98 11 69 D 9 8 E 94 9 B 1 E 87 E 9 CE 55 28 DF F 8 C A 1 89 0 D BF E 6 42 68 41 99 2 D 0 F B 0 54 BB 16 Figure 3. 8 The AES S-box 22

The Advanced Encryption Standard n n The AES S-box can be defined algebraically. The permutation incorporates operations in the finite field FIELDINV: the multiplicative inverse of a filed element BINARYTOFIELD: convert a byte to a field element FIELDTOBINARY: inverse operation n corresponds to the byte 23

The Advanced Encryption Standard n Algorithm 3. 4: SUBBYTES(a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0) external FIELDINV, BINARYTOFIELD, FIELDTOBINARYTOFILED(a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0) if then FIELDINV(z) (a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0) FIELDTOBINARY(z) (c 7 c 6 c 5 c 4 c 3 c 2 c 1 c 0) (01100011) comment: In the following loop, all subscripts are to be reduced modulo 8 for to 7 do return (b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0) 24

The Advanced Encryption Standard n Example 3. 5: (illustrates Algorithm 3. 4) n Suppose we begin with (hex) 53. In binary, it’s 01010011, which represents the field element The multiplicative inverse (in ) can be shown to be Thus we have 25

The Advanced Encryption Standard etc. The result is which is ED in hex. n This computation can be checked by verifying the entry in row 5 and column 3 of Figure 3. 8. 26
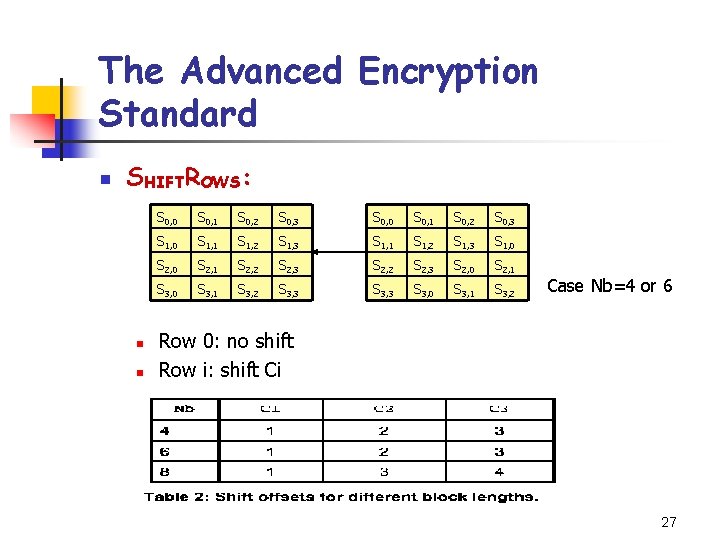
The Advanced Encryption Standard n SHIFTROWS: n n S 0, 0 S 0, 1 S 0, 2 S 0, 3 S 1, 0 S 1, 1 S 1, 2 S 1, 3 S 1, 0 S 2, 1 S 2, 2 S 2, 3 S 2, 0 S 2, 1 S 3, 0 S 3, 1 S 3, 2 S 3, 3 S 3, 0 S 3, 1 S 3, 2 Case Nb=4 or 6 Row 0: no shift Row i: shift Ci 27

The Advanced Encryption Standard n MIXCOLUMNS: (Algorithm 3. 5) n n n It is carried out on each of the four columns of State. Each column of State is replaced by a new column which is formed by multiplying that column by a certain matrix of elements of the field. FIELDMULT computes two inputs product in the field. Note: 2 is x in and 3 is x+1 in 28

The Advanced Encryption Standard n Algorithm 3. 5: MIXCOLUMN(c) external FIELDMULT, BINARYTOFIELD, FIELDTOBINARY for to 3 do BINARYTOFIELD(si, c) u 0 FIELDMULT(x, t 0) FIELDMULT(x+1, t 1) t 2 u 1 FIELDMULT(x, t 1) FIELDMULT(x+1, t 2) t 3 u 2 FIELDMULT(x, t 2) FIELDMULT(x+1, t 3) t 0 u 3 FIELDMULT(x, t 3) FIELDMULT(x+1, t 0) t 1 for to 3 do si, c FIELDTOBINARY(ui) t 3 t 0 t 1 t 2 29

The Advanced Encryption Standard n KEYEXPANSION: (for 10 -round AES) n n n 10 -round, 128 -bit key We need 11 round keys, each of 16 bytes Key scheduling algorithm is word-oriented (4 bytes), so a round key consists of 4 words The concatenation of round keys is called the expanded key, which consists of 44 words, w[0], w[1], …, w[43]. See Algorithm 3. 6 30

The Advanced Encryption Standard n Notations of Algorithm 3. 6: n n n Input: 128 -bit key, key[0], …, key[15] Output: words, w ROTWORD: a cyclic shift of four bytes B 0, B 1, B 2, B 3 ROTWORD (B 0, B 1, B 2, B 3)= (B 1, B 2, B 3, B 0) SUBWORD: applies the S-box to each byte SUBWORD (B 0, B 1, B 2, B 3)=(B 0’, B 1’, B 2’, B 3’) where Bi’=SUBBYTES(Bi) RCon: an array of 10 words, RCon[1], …, RCon[10], they are constants defined at the beginning 31
![Algorithm 3. 6: KEYEXPANSION(key) external ROTWORD, SUBWORD RCon[1] 01000000 RCon[2] 02000000 RCon[3] 04000000 RCon[4] Algorithm 3. 6: KEYEXPANSION(key) external ROTWORD, SUBWORD RCon[1] 01000000 RCon[2] 02000000 RCon[3] 04000000 RCon[4]](http://slidetodoc.com/presentation_image/1b8090741c944d1ddf18413f77d524db/image-32.jpg)
Algorithm 3. 6: KEYEXPANSION(key) external ROTWORD, SUBWORD RCon[1] 01000000 RCon[2] 02000000 RCon[3] 04000000 RCon[4] 08000000 RCon[5] 10000000 RCon[6] 20000000 RCon[7] 40000000 RCon[8] 80000000 RCon[9] 1 B 000000 RCon[10] 36000000 for to 3 do w[i] (key[4 i], key[4 i+1], key[4 i+2], key[4 i+3]) for to 43 do temp w[i-1] if 0 (mod 4) then temp SUBWORD(ROTWORD(temp)) RCon[1/4] w[i-4] temp return (w[0], …, w[43]) 32

The Advanced Encryption Standard n n n Above are the operations need to encrypt in AES. To decrypt, we perform all operations and the key schedule in the reverse order. Each operation, SHIFTROWS, SUBBYTES, MIXCOLUMNS must be replaced by their inverse operations. n ADDROUNDKEY is its own reverse. 33

The Advanced Encryption Standard n 3. 6. 2 Analysis of AES n n AES is secure against all known attacks. Various aspects of design incorporate specific features to against specific attacks. n n Ex 1: Finite field inversion in S-box yields linear approximation and difference distribution tables close to uniform. Ex 2: MIXCOLUMNS makes it impossible to find differential and linear attacks that involve “few” active S-boxes (wide trail strategy). 34

3. 7 Modes of Operation n Four modes of operation for DES: n n n Electronic codebook mode (ECB mode) Cipher feedback mode (CFB mode) Cipher block chaining mode (CBC mode) Output feedback mode (OFB mode) ECB mode corresponds to the naive use of a block cipher: n x 1, x 2, …of 64 -bit plaintext blocks, encrypted with the same key K, producing a string of ciphertext blocks, y 1, y 2, … 35
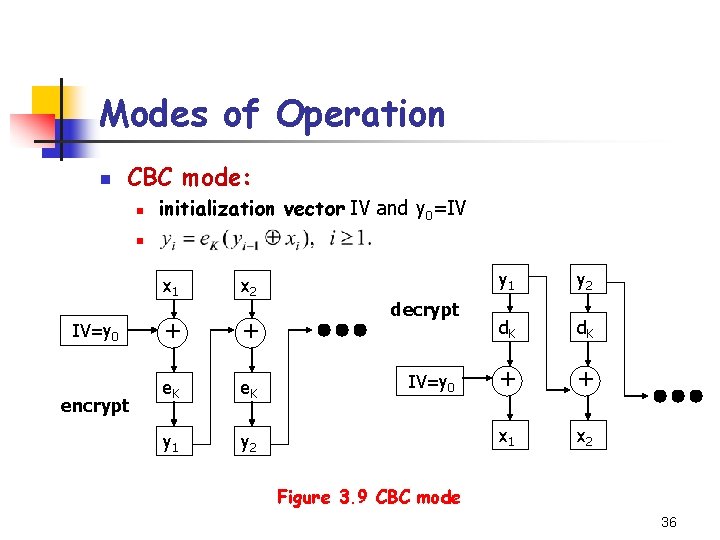
Modes of Operation n CBC mode: n initialization vector IV and y 0=IV n IV=y 0 encrypt x 1 x 2 + + e. K y 1 y 2 decrypt IV=y 0 y 1 y 2 d. K + + x 1 x 2 Figure 3. 9 CBC mode 36
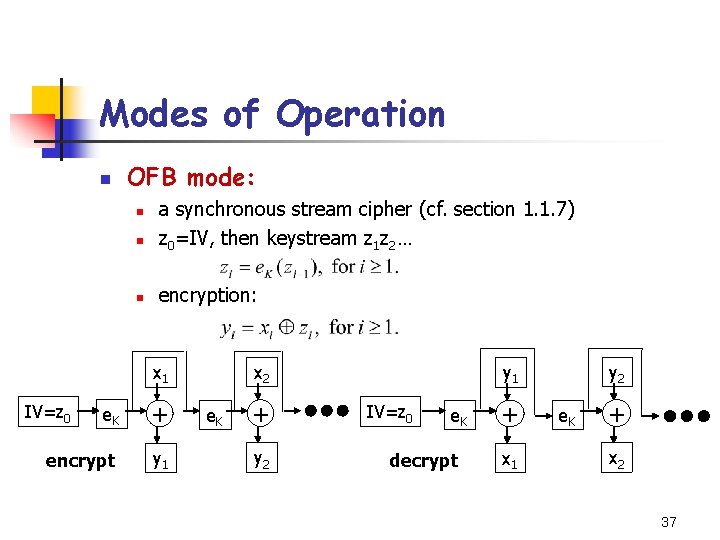
Modes of Operation n OFB mode: n a synchronous stream cipher (cf. section 1. 1. 7) z 0=IV, then keystream z 1 z 2… n encryption: n x 2 x 1 e. K + encrypt y 1 IV=z 0 e. K + y 2 y 1 IV=z 0 e. K decrypt + x 1 e. K + x 2 37
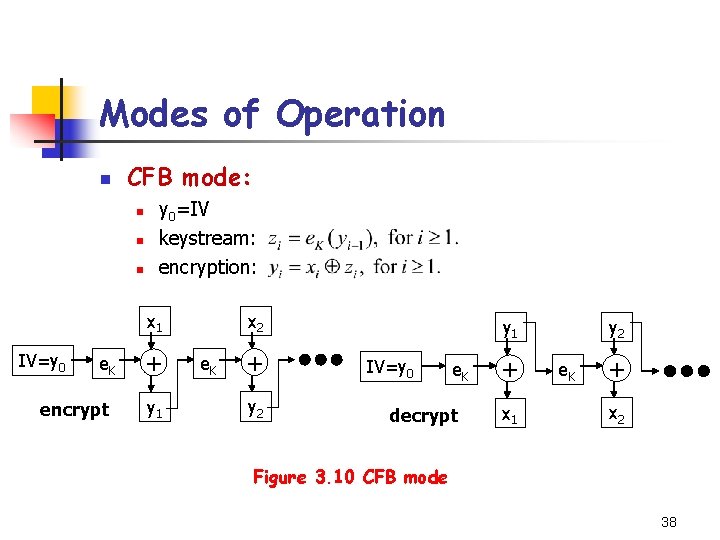
Modes of Operation n CFB mode: n n n y 0=IV keystream: encryption: x 2 x 1 IV=y 0 e. K encrypt + y 1 e. K + y 2 y 1 IV=y 0 e. K decrypt + x 1 e. K + x 2 Figure 3. 10 CFB mode 38

Modes of Operation n Some properties: n In ECB and OFB modes, changing one 64 -bit plaintext block, xi, causes the corresponding ciphertext block, yi, to be altered, but other ciphertext blocks are not affected. n n It is useful in some cases, like communicating on an unreliable channel. In CBC and CFB modes, if a plaintext block xi is changed, then yi and all subsequent ciphertext blocks will be affected. n These modes can be used to produce a message authentication code (MAC). (see Chap 4) 39
- Slides: 39