Chapter 3 Block Ciphers and the Advanced Encryption

Chapter 3 Block Ciphers and the Advanced Encryption Standard 1

Outline n n n n 3. 1 3. 2 3. 3 3. 4 3. 5 3. 6 3. 7 Introduction Substitution-Permutation Networks Linear cryptanalysis Differential cryptanalysis The Data Encryption Standard The Advanced Encryption Standard Modes of Operation 2

3. 1 Introduction n A commonly used design for modern-day block ciphers is that of an iterated cipher: n The cipher requires the specification of a round function and a key schedule, and the encryption of a plaintext will proceed through Nr similar rounds. 3

Introduction n n random key K: used to construct Nr round keys (also called subkeys), which are denoted K 1, …, KNr. key schedule (K 1, …, KNr): constructed from K using a fixed, public algorithm. round function g: takes two inputs: a round key (Kr) and a current state (wr-1). wr=g(wr-1, Kr) is the next state. plaintext x: the initial state w 0. ciphertext y: the state after all Nr rounds done. 4

Introduction n Encryption operations: Decryption operations: Note: function g is injective (one-to-one) 5

3. 2 Substitution-Permutation Networks (SPN) n Cryptosystem 3. 1: SPN n n n and Nr are positive integers is a permutation. , and consist of all possible key schedules that could be derived from an initial key K using the key scheduling algorithm. For a key schedule , we encrypt the plaintext x using Algorithm 3. 1. 6

Substitution-Permutation Networks n Algorithm 3. 1: SPN ur is the input to the Sboxes in round r. vr is the output of the Sboxes in round r. wr is obtained from vr by applying. ur+1 is constructed from wr by xor-ing with the round key Kr+1 (called round key mixing). The very first and last operations are xors with subkeys (called whitening). 7

Substitution-Permutation Networks n Example 3. 1: n Suppose. Let be defined as follows, where the input and the output are written in hexadecimal: Let be defined as follows: See Figure 3. 1 for a pictorial representation of this particular SPN, where Sir means i-th round, r-th S-box. 8
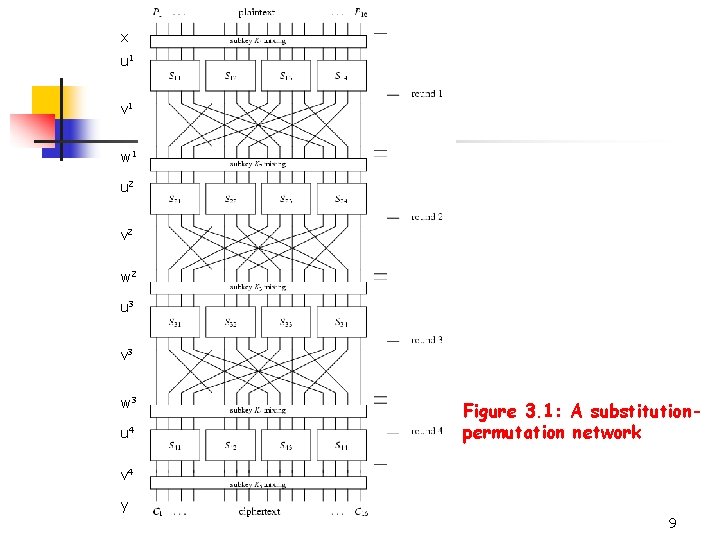
x u 1 v 1 w 1 u 2 v 2 w 2 u 3 v 3 w 3 u 4 Figure 3. 1: A substitutionpermutation network v 4 y 9

Substitution-Permutation Networks n n n Key schedule: suppose we begin with a 32 -bit key. For , define Kr to consist of 16 consecutive bits of K, beginning with k 4 r-3. K= 0011 1010 1001 0100 1101 0110 0011 1111 Round keys: K 1= 0011 1010 1001 0100 K 2= 1010 1001 0100 1101 K 3= 1001 0100 1101 0110 K 4= 0100 1101 0110 0011 K 5= 1101 0110 0011 1111 10

Substitution-Permutation Networks n n Suppose the plaintext is x= 0010 0110 1011 0111. Then the encryption of x proceeds as follows: w 0= 0010 0110 1011 0111 K 1= 0011 1010 1001 0100 u 1= 0001 1100 0011 v 1= 0100 0101 1101 0001 w 1= 0010 1110 0000 0111 K 2= 1010 1001 0100 1101 u 2= 1000 0111 0100 1010 v 2= 0011 1000 0010 0110 w 2= 0100 0001 1011 1000 11

Substitution-Permutation Networks K 3= 1001 0100 1101 0110 u 3= 1101 0110 1110 v 3= 1001 1111 1011 0000 w 3= 1110 0100 0110 1110 K 4= 0100 1101 0110 0011 u 4= 1010 1001 0000 1101 v 4= 0110 1010 1110 1001 K 5= 1101 0110 0011 1111, and y= 1011 1100 1101 0110 is the ciphertext. 12

3. 3 Linear Cryptanalysis n n n We want to find a probabilistic linear relationship between a subset of plaintext bits and a subset of data bits preceding the last round. This relation behaves in a non-random fashion. The attacker has a lot of plaintext-ciphertext pairs (known plaintext attack). For each candidate subkey, we partially decrypt the cipher and check if the relation holds. If the relation holds then increment its corresponding counter. At the end, the candidate key that counts furthest from ½ is the most likely subkey. 13

Linear Cryptanalysis n 3. 3. 1 The Piling-up Lemma n n Suppose X 1, X 2, … are independent random variables from {0, 1}. And The independence of Xi, Xj implies 14

Linear Cryptanalysis n Now consider . n The bias of Xi is defined to be the quantity n And we have 15

Linear Cryptanalysis n n Let denote the bias of Lemma 3. 1 (Piling-up lemma) : Let the bias of the random variable Corollary 3. 2: Let random variable some j. Then . . denote. Then denote the bias of the. Suppose that for 16

Linear Cryptanalysis n 3. 3. 2 Linear Approximations of S-boxes n Consider an S-box. Let the input m-tuple be X=(x 1, …, xm). And the output n-tuple be Y=(y 1, …, yn). We can see that n Now we can compute the bias of the form n n using the formulas stated above. 17
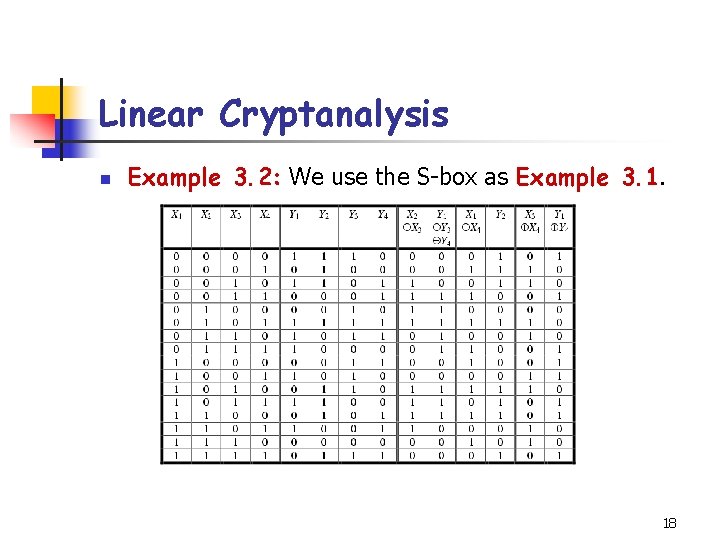
Linear Cryptanalysis n Example 3. 2: We use the S-box as Example 3. 1. 18

Linear Cryptanalysis n n n Consider. The probability that can be determined by counting the number of rows in which , and then dividing by 16. It is seen that Hence, the bias is 0. If we instead analyze is – 3/8. , we find that the bias 19

Linear Cryptanalysis n n n We can record the bias of all 28=256 possible random variables. We represent the relevant random variable in the form where. We treat (a 1, a 2, a 3, a 4) and (b 1, b 2, b 3, b 4) as hexadecimal digit (they are called input sum and output sum, respectively) 20

Linear Cryptanalysis n Let NL(a, b) denote the number of binary eight-tuples (x 1, x 2, x 3, x 4, y 1, y 2, y 3, y 4) s. t and n n The bias is computed as. The table of all NL is called the linear approximation table (Figure 3. 2). 21
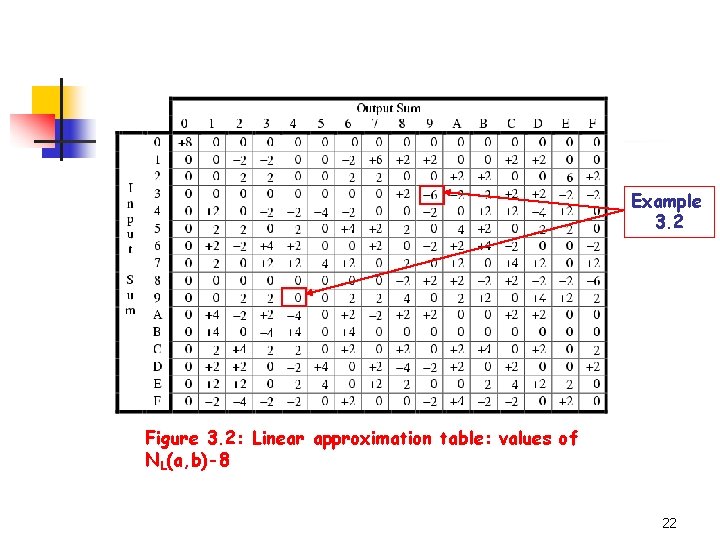
Example 3. 2 Figure 3. 2: Linear approximation table: values of NL(a, b)-8 22

Linear Cryptanalysis n 3. 3. 3 Linear Attack on an SPN n n Linear cryptanalysis requires a set of linear approximations of S-boxes that can be used to derive a linear approximation of the entire SPN (excluding the last round). Figure 3. 3 illustrates the structure of the approximation we will use. n Arrows are the random variables involved in the approximations and the labeled S-boxes (active S-boxes) are used in the approximations. 23
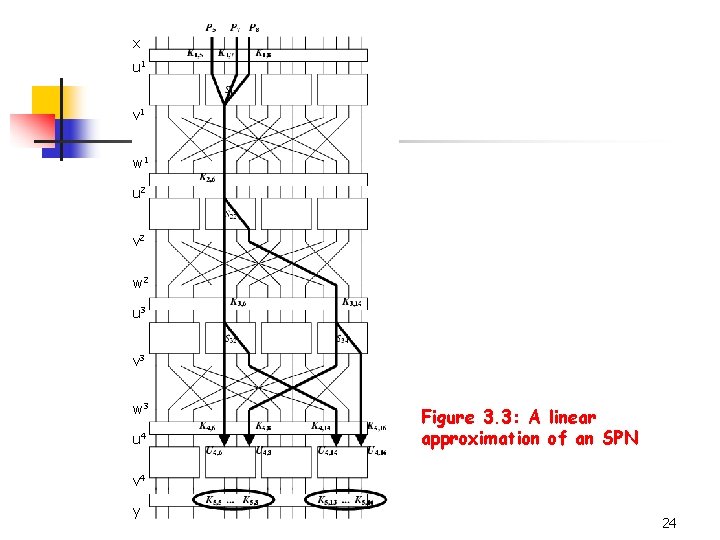
x u 1 v 1 w 1 u 2 v 2 w 2 u 3 v 3 w 3 u 4 Figure 3. 3: A linear approximation of an SPN v 4 y 24

Linear Cryptanalysis n The approximation incorporates four active S-boxes: n n n In In S 12, S 22, S 34, has bias ¼ has bias -¼ have biases that are high in absolute value. Further, we will see their XOR will lead to cancellations of “intermediate” random variables. 25

Linear Cryptanalysis n Using Piling-up lemma, to 23(1/4)(-1/4)3=-1/32. n n has bias equal Note: we assume the four r. v are independent. Then can be expressed in terms of plaintext bits, bits of u 4 (input to the last round) and key bits as follows: 26

Linear Cryptanalysis n XOR the right side and we get n Then replace n Now substitute them into 3. 1: by and key bits: 27

Linear Cryptanalysis n The expression above only involves plaintext bits, bits of u 4 and key bits. Suppose the key bits are fixed. Then n has the (fixed) value 0 or 1. It follows that n has bias -1/32 or 1/32 where the sign depends on the key bits (=0 or =1). 28

Linear Cryptanalysis n n n The fact that (3. 3) has bias bounded away from 0 allows us to carry out linear attack. Suppose that we have T plaintext-ciphertext pairs (denoted by ), all use the same unknown key, K. The attack will allow us to obtain the eight key bits, There are 28=256 possibilities for the eight key bits. We refer to a binary 8 -tuple as a candidate subkey. 29

Linear Cryptanalysis n n For each and for each candidate subkey, we compute a partial decryption of y and obtain the resulting value for. Then we compute the value We maintain an array of counters indexed by the 256 possible candidate subkeys, and increment the counter corresponding to a particular subkey when (3. 4) has the value 0. In the end, we expect most counters will have a value close to T/2, but the correct candidate subkey will close to T/2±T/32. 30

Linear Cryptanalysis n The attack is presented as Algorithm 3. 2. n n L 1 and L 2 are hexadecimal value. is the inverse of the S-box. The output, maxkey, contains the most likely subkey. In general, it is suggested that a linear attack based on a linear approximation having bias will be successful if the number of plaintext-ciphertext pairs is approximately for some “small” constant c. 31

Algorithm 3. 2: LINEARATTACK( ) 32

3. 5 The Data Encryption Standard n n n DES was developed at IBM, as a modification of an earlier system known as Lucifer. DES was first published in the Federal Register of March 17, 1975. DES was adopted as a standard for “unclassified” applications on January 15, 1977. 33

The Data Encryption Standard n 3. 5. 1 Description of DES n DES is a special type of iterated cipher called a Feistel cipher. n In a Feistel cipher, each state ui is divided into two halves of equal length, say Li and Ri. Round function g: g(Li-1, Ri-1, Ki)=(Li, Ri), where n Invertible: n 34
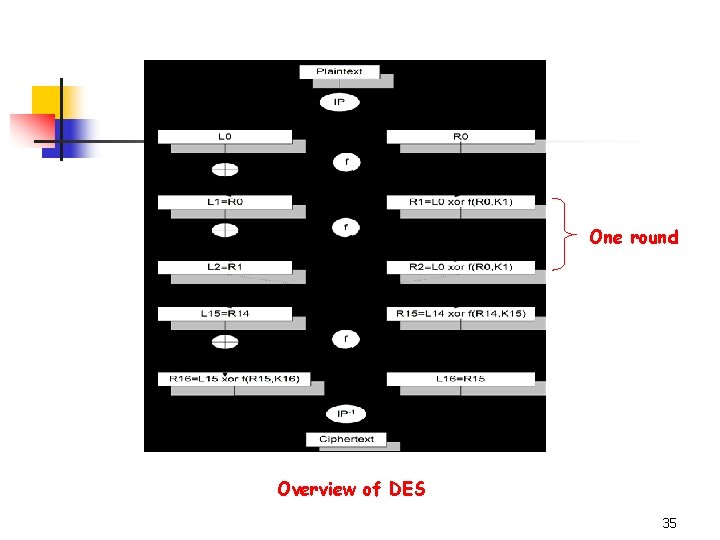
One round Overview of DES 35

The Data Encryption Standard n n Initial permutation IP: IP(x)=L 0 R 0 Inverse permutation IP-1: y=IP-1(R 16 L 16) n n Note L 16 and R 16 are swapped before IP-1 is applied. Each Li and Ri is 32 bits in length. The function takes as input a 32 -bit string (the right half of the current state) and a round key. Key schedule (K 1, K 2, …, K 16) consists of 48 -bit round keys that are derived from the 56 -bit key, K. 36

The Data Encryption Standard n Suppose we denote the first argument of f function (Figure 3. 7) by A, and the second argument by J. n n A is expanded to 48 -bit according to a fixed expansion function E. Compute and write the result as concatenation of eight 6 -bit strings B=B 1 B 2 B 3 B 4 B 5 B 6 B 7 B 8. The next step uses eight S-boxes (S 1, …, S 8), Given a bitstring of length 6, Bj=b 1 b 2 b 3 b 4 b 5 b 6. b 1 b 6 determine the row r of Sj, and b 2 b 3 b 4 b 5 determine the column c of Sj. We compute Cj=Sj(Bj). The bitstring C=C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 is permuted according to the permutation P. Then f (A, J)=P(C). 37
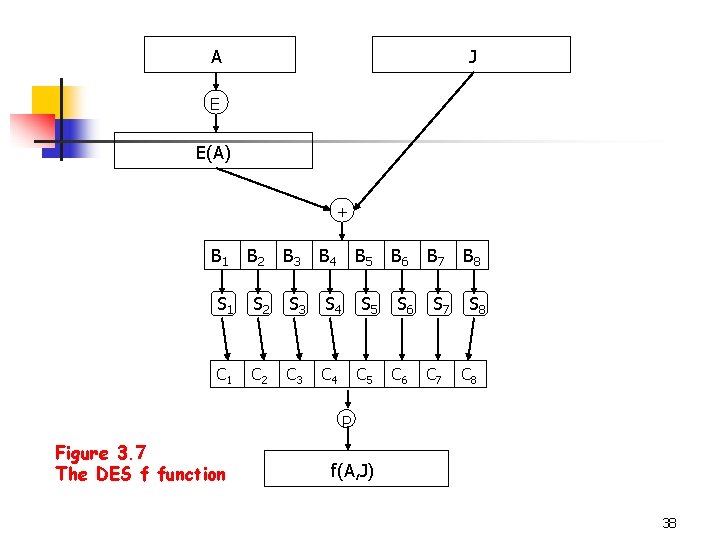
A J E E(A) + B 1 B 2 B 3 B 4 B 5 S 1 S 2 S 3 S 4 S 5 C 1 C 2 C 3 C 4 C 5 B 6 S 6 C 6 B 7 S 7 C 7 B 8 S 8 C 8 P Figure 3. 7 The DES f function f(A, J) 38
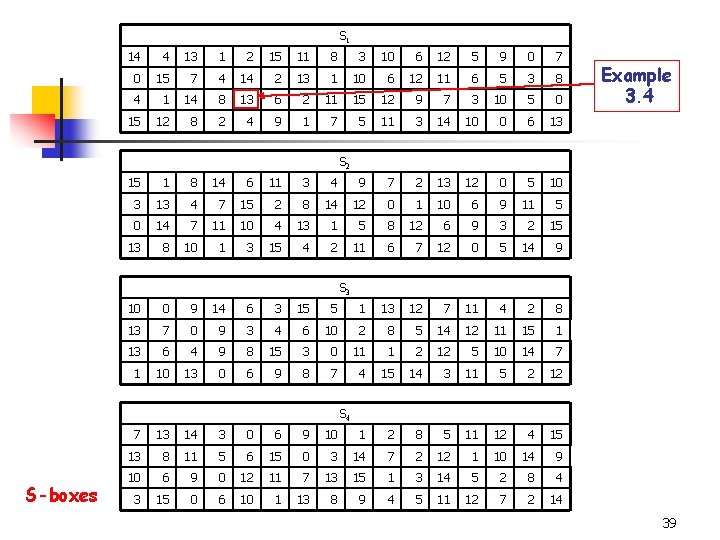
S 1 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 0 15 7 4 14 2 13 1 10 6 12 11 6 5 3 8 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13 Example 3. 4 S 2 15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9 S 3 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8 13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12 S 4 S-boxes 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15 13 8 11 5 6 15 0 3 14 7 2 12 1 10 14 9 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4 3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14 39
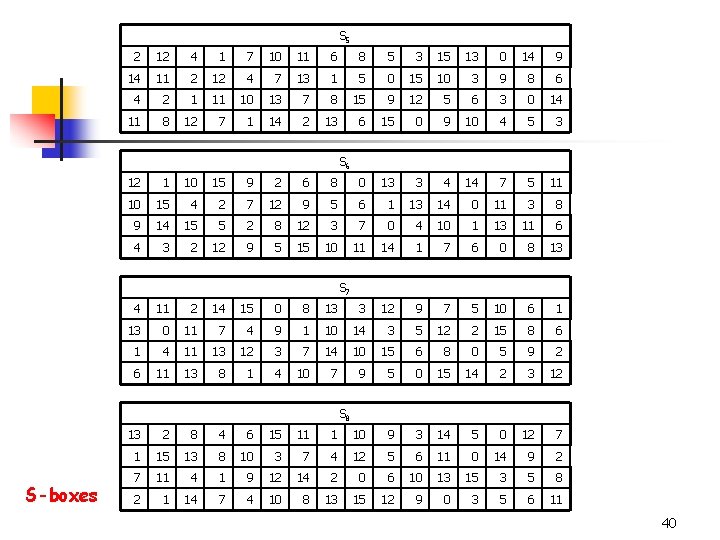
S 5 2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6 4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14 11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3 S 6 12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11 10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13 S 7 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12 S 8 S-boxes 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11 40

The Data Encryption Standard n Example 3. 4: We show to compute an output of S-box S 1 with input 101000. n n n b 1 b 6=10 which is 2 b 2 b 3 b 4 b 5=1000 which is 4 Output is row 2 and column 4 of S 1. n n Note: rows are numbered 0, 1, 2, 3 and columns are 0, 1, 2, … 15 So the output is 13 which is 1101 in binary. 41

The Data Encryption Standard n n The expansion function E is specified by the following table: E bit-selection table 32 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 1 If A=(a 1, a 2, …, a 32) then E(A)=(a 32, a 1, a 2, a 3, a 4, a 5, a 4, …, a 31, a 32, a 1). 42

The Data Encryption Standard n The permutation P is as follows: P n 16 7 20 21 29 12 28 17 1 15 23 26 5 18 31 10 2 8 24 14 32 27 3 9 19 13 30 6 22 11 4 25 If C=(c 1, c 2, …, c 32) then P(C)=(c 16, c 7, c 20, c 21, c 29, …, c 11, c 4, c 25). 43
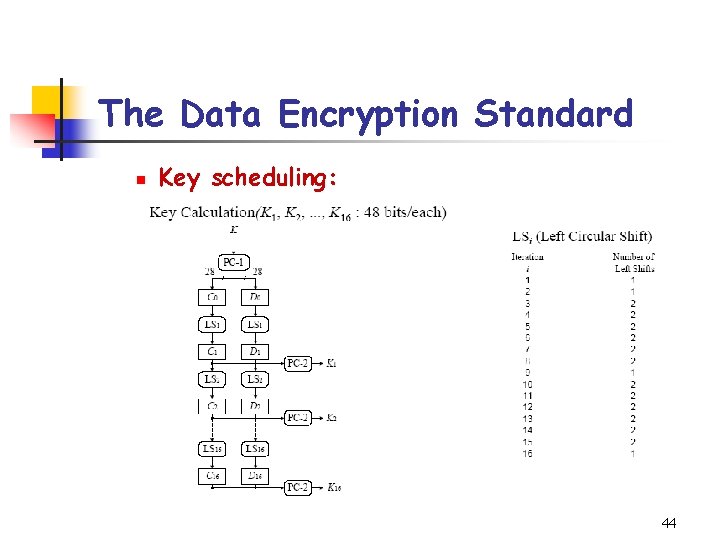
The Data Encryption Standard n Key scheduling: 44

The Data Encryption Standard 45

The Data Encryption Standard n 3. 5. 2: Analysis of DES n n The S-boxes, being the non-linear components of the cryptosystem, are vital to its security. DES was to make differential cryptanalysis infeasible. n n Differential cryptanalysis was known to IBM when they design DES, but it was kept secret for almost 20 years until Biham and Shamir invented the technique in the early 1990’s. The most pertinent criticism of DES is that the size of the keyspace, 256, is too small. 46

The Data Encryption Standard n Many people try to design a special purpose machine to do exhaustive key search. n n Ex: “DES Cracker” contained 1536 chips and could search 88 billion keys per second. It won RSA Laboratory’s “DES Challenge II-2” by successfully finding a DES key in 56 hours. Other than exhaustive key search, differential cryptanalysis and linear cryptanalysis are the most important attacks. (linear attack is more efficient) n n In 1994, Matsui implemented the attack by using 243 plaintextciphertext pairs with the same key. It took 40 days to generate the pairs and 10 days to find the key. DES is still secure theoretically due to the extremely large number of pairs required. An adversary is impossible to collect that amount of pairs. 47

3. 6 The Advanced Encryption Standard n n n On January 2, 1997, NIST began the process of choosing a replacement for DES and called the Advanced Encryption Standard, or AES. It was required that the AES have a block length of 128 bits, and supported key lengths of 128, 192, and 256 bits. After several AES candidate conferences were held. On Oct. 2, 2000, Rijndael was selected. n 3 main criteria: security, cost, algorithm and implementation characteristics 48

The Advanced Encryption Standard n 3. 6. 1 Description of AES n Block length: n n Key length: n n 128 bits (Nb=4) 192 bits (Nb=6) 256 bits (Nb=8) S 0, 0 S 0, 1 S 0, 2 S 0, 3 S 0, 4 S 0, 5 S 0, 6 S 0, 7 S 1, 0 S 1, 1 S 1, 2 S 1, 3 S 1, 4 S 1, 5 S 1, 6 S 1, 7 S 2, 0 S 2, 1 S 2, 2 S 2, 3 S 2, 4 S 2, 5 S 2, 6 S 2, 7 S 3, 0 S 3, 1 S 3, 2 S 3, 3 S 3, 4 S 3, 5 S 3, 6 S 3, 7 128 bits (Nk=4) 192 bits (Nk=6) 256 bits (Nk=8) Number of rounds Nr: 49

The Advanced Encryption Standard n Overview of AES: n ADDROUNDKEY, which xors the Round. Key with State. For each of the first Nr-1 rounds: perform SUBBYTES(State), SHIFTROWS(State), MIXCOLUMN(State), ADDROUNDKEY. n Final round: SUBBYTES, SHIFTROWS, ADDROUNDKEY. n n All operations in AES are byte-oriented. n n The plaintext x consists of 16 byte, x 0, x 1, …, x 15. Initially State is plaintext x (for 128 -bit case): S 0, 0 S 0, 1 S 0, 2 S 0, 3 x 0 x 4 x 8 x 12 S 1, 0 S 1, 1 S 1, 2 S 1, 3 x 1 x 5 x 9 x 13 S 2, 0 S 2, 1 S 2, 2 S 2, 3 x 2 x 6 x 10 x 14 S 3, 0 S 3, 1 S 3, 2 S 3, 3 x 7 x 11 x 15 50
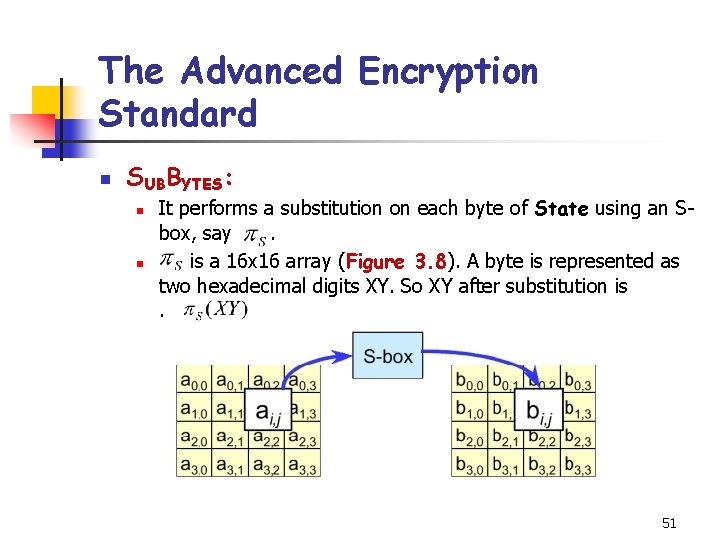
The Advanced Encryption Standard n SUBBYTES: n n It performs a substitution on each byte of State using an Sbox, say. is a 16 x 16 array (Figure 3. 8). A byte is represented as two hexadecimal digits XY. So XY after substitution is. 51
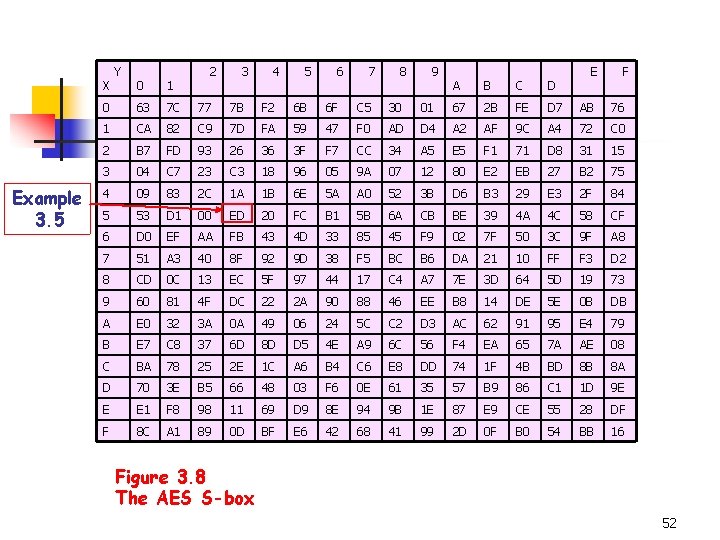
X Example 3. 5 Y 2 3 4 5 6 7 8 0 1 0 63 7 C 77 7 B F 2 6 B 6 F C 5 30 1 CA 82 C 9 7 D FA 59 47 F 0 2 B 7 FD 93 26 36 3 F F 7 3 04 C 7 23 C 3 18 96 4 09 83 2 C 1 A 1 B 5 53 D 1 00 ED 6 D 0 EF AA 7 51 A 3 8 CD 9 9 E F A B C D 01 67 2 B FE D 7 AB 76 AD D 4 A 2 AF 9 C A 4 72 C 0 CC 34 A 5 E 5 F 1 71 D 8 31 15 05 9 A 07 12 80 E 2 EB 27 B 2 75 6 E 5 A A 0 52 3 B D 6 B 3 29 E 3 2 F 84 20 FC B 1 5 B 6 A CB BE 39 4 A 4 C 58 CF FB 43 4 D 33 85 45 F 9 02 7 F 50 3 C 9 F A 8 40 8 F 92 9 D 38 F 5 BC B 6 DA 21 10 FF F 3 D 2 0 C 13 EC 5 F 97 44 17 C 4 A 7 7 E 3 D 64 5 D 19 73 60 81 4 F DC 22 2 A 90 88 46 EE B 8 14 DE 5 E 0 B DB A E 0 32 3 A 0 A 49 06 24 5 C C 2 D 3 AC 62 91 95 E 4 79 B E 7 C 8 37 6 D 8 D D 5 4 E A 9 6 C 56 F 4 EA 65 7 A AE 08 C BA 78 25 2 E 1 C A 6 B 4 C 6 E 8 DD 74 1 F 4 B BD 8 B 8 A D 70 3 E B 5 66 48 03 F 6 0 E 61 35 57 B 9 86 C 1 1 D 9 E E E 1 F 8 98 11 69 D 9 8 E 94 9 B 1 E 87 E 9 CE 55 28 DF F 8 C A 1 89 0 D BF E 6 42 68 41 99 2 D 0 F B 0 54 BB 16 Figure 3. 8 The AES S-box 52

The Advanced Encryption Standard n n The AES S-box can be defined algebraically. The permutation incorporates operations in the finite field FIELDINV: the multiplicative inverse of a filed element BINARYTOFIELD: convert a byte to a field element FIELDTOBINARY: inverse operation n corresponds to the byte 53

The Advanced Encryption Standard n Algorithm 3. 4: SUBBYTES(a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0) external FIELDINV, BINARYTOFIELD, FIELDTOBINARYTOFILED(a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0) if then FIELDINV(z) (a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0) FIELDTOBINARY(z) (c 7 c 6 c 5 c 4 c 3 c 2 c 1 c 0) (01100011) comment: In the following loop, all subscripts are to be reduced modulo 8 for to 7 do return (b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0) 54

The Advanced Encryption Standard n Example 3. 5: (illustrates Algorithm 3. 4) n Suppose we begin with (hex) 53. In binary, it’s 01010011, which represents the field element The multiplicative inverse (in ) can be shown to be Thus we have 55

The Advanced Encryption Standard etc. The result is which is ED in hex. n This computation can be checked by verifying the entry in row 5 and column 3 of Figure 3. 8. 56
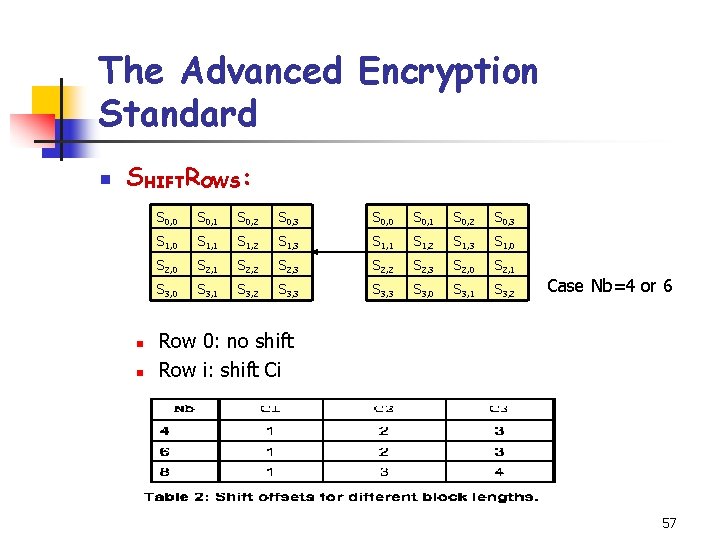
The Advanced Encryption Standard n SHIFTROWS: n n S 0, 0 S 0, 1 S 0, 2 S 0, 3 S 1, 0 S 1, 1 S 1, 2 S 1, 3 S 1, 0 S 2, 1 S 2, 2 S 2, 3 S 2, 0 S 2, 1 S 3, 0 S 3, 1 S 3, 2 S 3, 3 S 3, 0 S 3, 1 S 3, 2 Case Nb=4 or 6 Row 0: no shift Row i: shift Ci 57

The Advanced Encryption Standard n MIXCOLUMNS: (Algorithm 3. 5) n n n It is carried out on each of the four columns of State. Each column of State is replaced by a new column which is formed by multiplying that column by a certain matrix of elements of the field. FIELDMULT computes two inputs product in the field. Note: 2 is x in and 3 is x+1 in 58

The Advanced Encryption Standard n Algorithm 3. 5: MIXCOLUMN(c) external FIELDMULT, BINARYTOFIELD, FIELDTOBINARY for to 3 do BINARYTOFIELD(si, c) u 0 FIELDMULT(x, t 0) FIELDMULT(x+1, t 1) t 2 u 1 FIELDMULT(x, t 1) FIELDMULT(x+1, t 2) t 3 u 2 FIELDMULT(x, t 2) FIELDMULT(x+1, t 3) t 0 u 3 FIELDMULT(x, t 3) FIELDMULT(x+1, t 0) t 1 for to 3 do si, c FIELDTOBINARY(ui) t 3 t 0 t 1 t 2 59

The Advanced Encryption Standard n KEYEXPANSION: (for 10 -round AES) n n n 10 -round, 128 -bit key We need 11 round keys, each of 16 bytes Key scheduling algorithm is word-oriented (4 bytes), so a round key consists of 4 words The concatenation of round keys is called the expanded key, which consists of 44 words, w[0], w[1], …, w[43]. See Algorithm 3. 6 60

The Advanced Encryption Standard n Notations of Algorithm 3. 6: n n n Input: 128 -bit key, key[0], …, key[15] Output: words, w ROTWORD: a cyclic shift of four bytes B 0, B 1, B 2, B 3 ROTWORD (B 0, B 1, B 2, B 3)= (B 1, B 2, B 3, B 0) SUBWORD: applies the S-box to each byte SUBWORD (B 0, B 1, B 2, B 3)=(B 0’, B 1’, B 2’, B 3’) where Bi’=SUBBYTES(Bi) RCon: an array of 10 words, RCon[1], …, RCon[10], they are constants defined at the beginning 61
![Algorithm 3. 6: KEYEXPANSION(key) external ROTWORD, SUBWORD RCon[1] 01000000 RCon[2] 02000000 RCon[3] 04000000 RCon[4] Algorithm 3. 6: KEYEXPANSION(key) external ROTWORD, SUBWORD RCon[1] 01000000 RCon[2] 02000000 RCon[3] 04000000 RCon[4]](http://slidetodoc.com/presentation_image_h/0c79daaf588474bf65c60cb0c4dbd961/image-62.jpg)
Algorithm 3. 6: KEYEXPANSION(key) external ROTWORD, SUBWORD RCon[1] 01000000 RCon[2] 02000000 RCon[3] 04000000 RCon[4] 08000000 RCon[5] 10000000 RCon[6] 20000000 RCon[7] 40000000 RCon[8] 80000000 RCon[9] 1 B 000000 RCon[10] 36000000 for to 3 do w[i] (key[4 i], key[4 i+1], key[4 i+2], key[4 i+3]) for to 43 do temp w[i-1] if 0 (mod 4) then temp SUBWORD(ROTWORD(temp)) RCon[1/4] w[i-4] temp return (w[0], …, w[43]) 62

The Advanced Encryption Standard n n n Above are the operations need to encrypt in AES. To decrypt, we perform all operations and the key schedule in the reverse order. Each operation, SHIFTROWS, SUBBYTES, MIXCOLUMNS must be replaced by their inverse operations. n ADDROUNDKEY is its own reverse. 63

The Advanced Encryption Standard n 3. 6. 2 Analysis of AES n n AES is secure against all known attacks. Various aspects of design incorporate specific features to against specific attacks. n n Ex 1: Finite field inversion in S-box yields linear approximation and difference distribution tables close to uniform. Ex 2: MIXCOLUMNS makes it impossible to find differential and linear attacks that involve “few” active S-boxes (wide trail strategy). 64

3. 7 Modes of Operation n Four modes of operation for DES: n n n Electronic codebook mode (ECB mode) Cipher feedback mode (CFB mode) Cipher block chaining mode (CBC mode) Output feedback mode (OFB mode) ECB mode corresponds to the naive use of a block cipher: n x 1, x 2, …of 64 -bit plaintext blocks, encrypted with the same key K, producing a string of ciphertext blocks, y 1, y 2, … 65
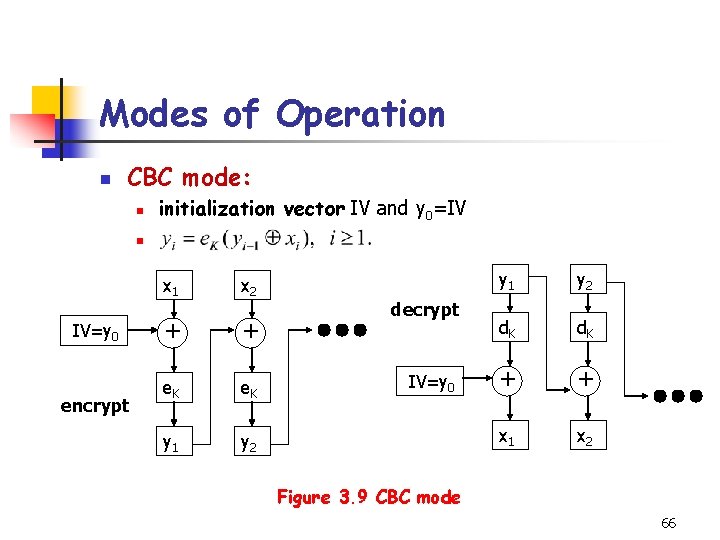
Modes of Operation n CBC mode: n initialization vector IV and y 0=IV n IV=y 0 encrypt x 1 x 2 + + e. K y 1 y 2 decrypt IV=y 0 y 1 y 2 d. K + + x 1 x 2 Figure 3. 9 CBC mode 66
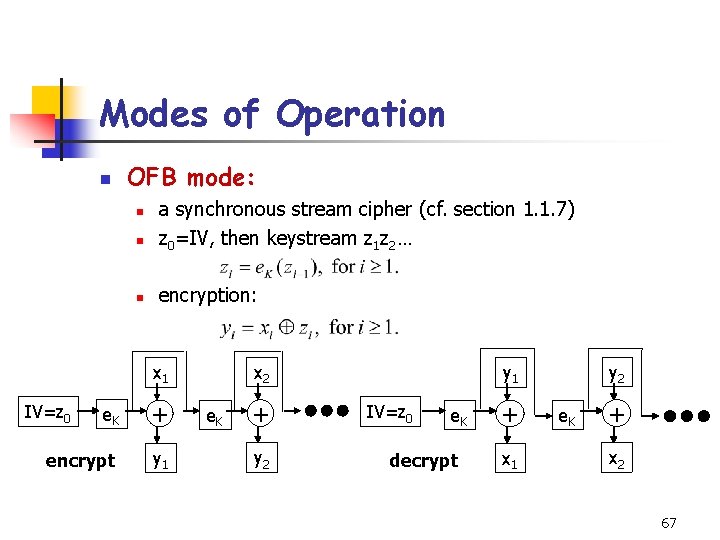
Modes of Operation n OFB mode: n a synchronous stream cipher (cf. section 1. 1. 7) z 0=IV, then keystream z 1 z 2… n encryption: n x 2 x 1 e. K + encrypt y 1 IV=z 0 e. K + y 2 y 1 IV=z 0 e. K decrypt + x 1 e. K + x 2 67
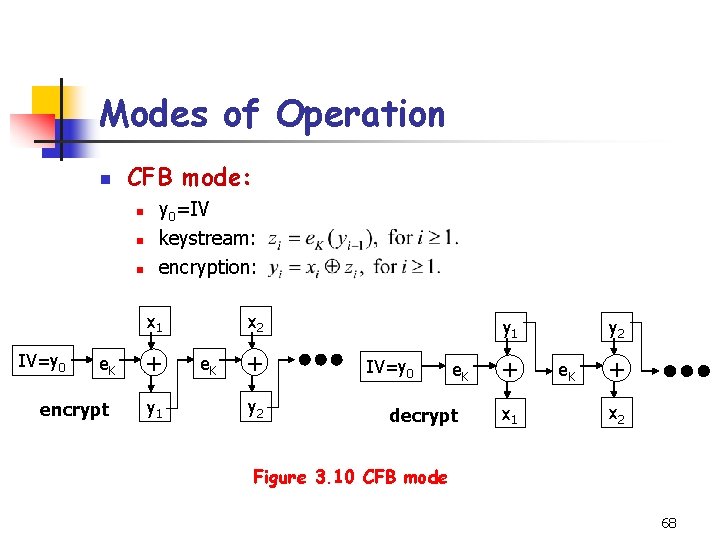
Modes of Operation n CFB mode: n n n y 0=IV keystream: encryption: x 2 x 1 IV=y 0 e. K encrypt + y 1 e. K + y 2 y 1 IV=y 0 e. K decrypt + x 1 e. K + x 2 Figure 3. 10 CFB mode 68

Modes of Operation n Some properties: n In ECB and OFB modes, changing one 64 -bit plaintext block, xi, causes the corresponding ciphertext block, yi, to be altered, but other ciphertext blocks are not affected. n n It is useful in some cases, like communicating on an unreliable channel. In CBC and CFB modes, if a plaintext block xi is changed, then yi and all subsequent ciphertext blocks will be affected. n These modes can be used to produce a message authentication code (MAC). (see Chap 4) 69
- Slides: 69