Chapter 3 Applications of Differentiation Definition of Extrema

Chapter 3 Applications of Differentiation

Definition of Extrema Copyright © Houghton Mifflin Company. All rights reserved. 3 -2

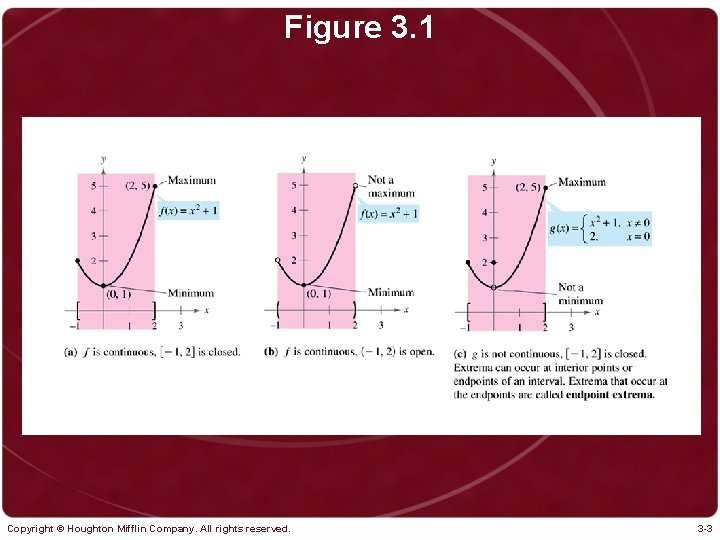
Figure 3. 1 Copyright © Houghton Mifflin Company. All rights reserved. 3 -3

Theorem 3. 1 The Extreme Value Theorem Copyright © Houghton Mifflin Company. All rights reserved. 3 -4

Definition of Relative Extrema Copyright © Houghton Mifflin Company. All rights reserved. 3 -5

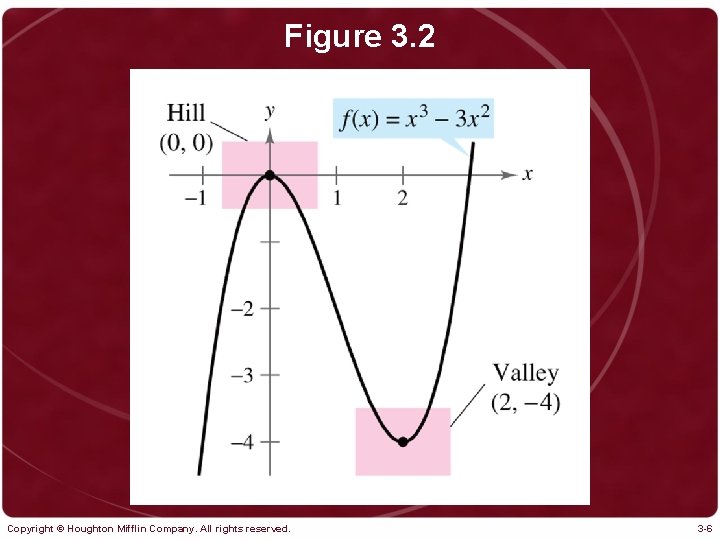
Figure 3. 2 Copyright © Houghton Mifflin Company. All rights reserved. 3 -6

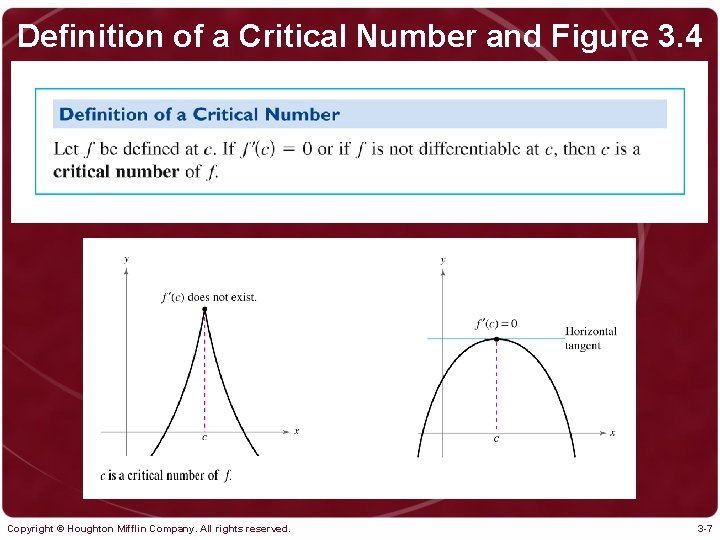
Definition of a Critical Number and Figure 3. 4 Copyright © Houghton Mifflin Company. All rights reserved. 3 -7

Theorem 3. 2 Relative Extrema Occur Only at Critical Numbers Copyright © Houghton Mifflin Company. All rights reserved. 3 -8

Guidelines for Finding Extrema on a Closed Interval Copyright © Houghton Mifflin Company. All rights reserved. 3 -9

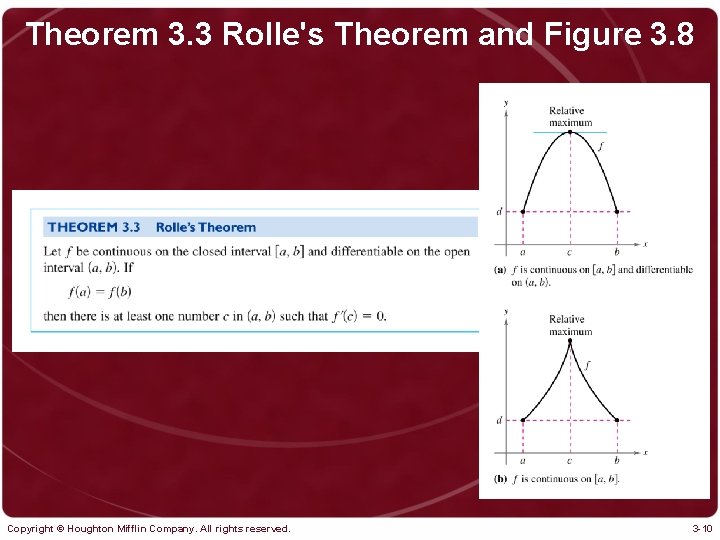
Theorem 3. 3 Rolle's Theorem and Figure 3. 8 Copyright © Houghton Mifflin Company. All rights reserved. 3 -10

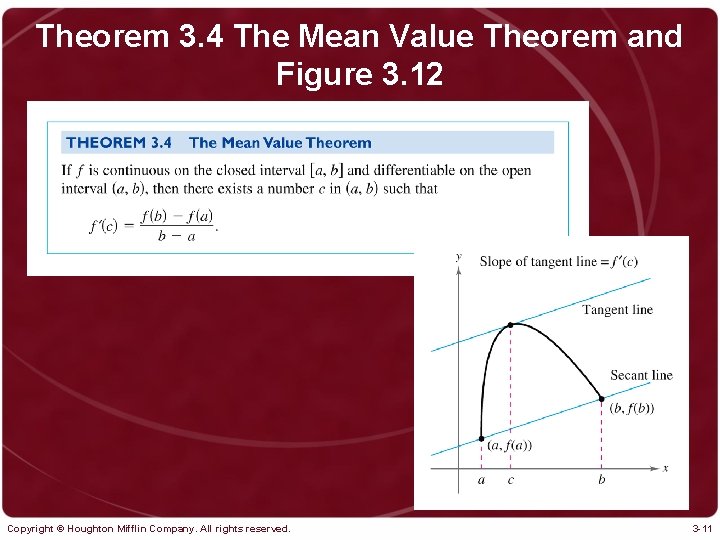
Theorem 3. 4 The Mean Value Theorem and Figure 3. 12 Copyright © Houghton Mifflin Company. All rights reserved. 3 -11

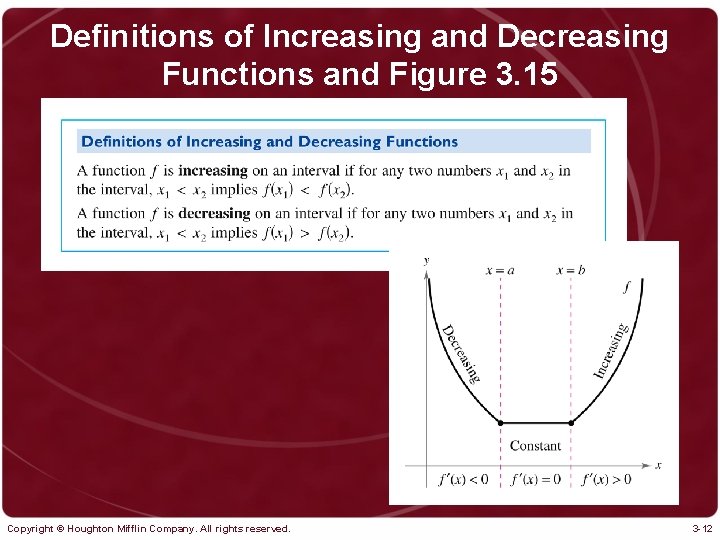
Definitions of Increasing and Decreasing Functions and Figure 3. 15 Copyright © Houghton Mifflin Company. All rights reserved. 3 -12

Theorem 3. 5 Test for Increasing and Decreasing Functions Copyright © Houghton Mifflin Company. All rights reserved. 3 -13

Guidelines for Finding Intervals on Which a Function Is Increasing or Decreasing Copyright © Houghton Mifflin Company. All rights reserved. 3 -14

Theorem 3. 6 The First Derivative Test Copyright © Houghton Mifflin Company. All rights reserved. 3 -15

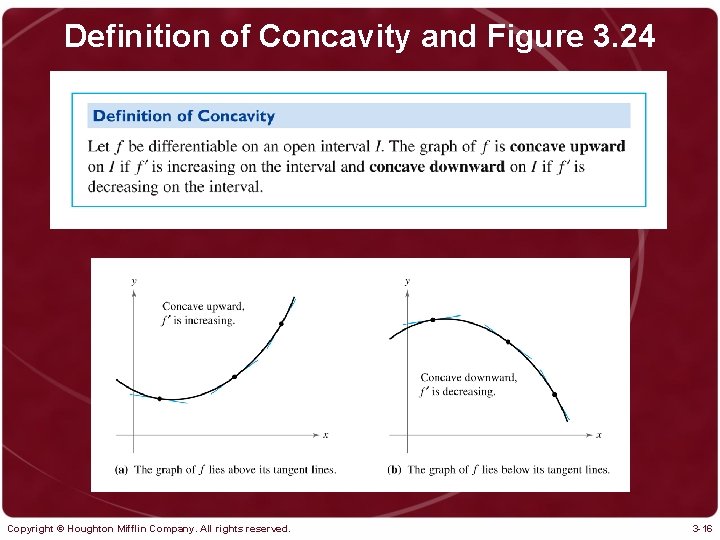
Definition of Concavity and Figure 3. 24 Copyright © Houghton Mifflin Company. All rights reserved. 3 -16

Theorem 3. 7 Test for Concavity Copyright © Houghton Mifflin Company. All rights reserved. 3 -17

Definition of Point of Inflection and Figure 3. 28 Copyright © Houghton Mifflin Company. All rights reserved. 3 -18

Theorem 3. 8 Points of Inflection Copyright © Houghton Mifflin Company. All rights reserved. 3 -19

Theorem 3. 9 Second Derivative Test and Figure 3. 31 Copyright © Houghton Mifflin Company. All rights reserved. 3 -20

Definition of Limits at Infinity and Figure 3. 34 Copyright © Houghton Mifflin Company. All rights reserved. 3 -21

Definition of a Horizontal Asymptote Copyright © Houghton Mifflin Company. All rights reserved. 3 -22

Theorem 3. 10 Limits at Infinity Copyright © Houghton Mifflin Company. All rights reserved. 3 -23

Guidelines for Finding Limits at +/- infinity of Rational Functions Copyright © Houghton Mifflin Company. All rights reserved. 3 -24

Definition of Infinite Limits at Infinity Copyright © Houghton Mifflin Company. All rights reserved. 3 -25

Guidelines for Analyzing the Graph of a Function Copyright © Houghton Mifflin Company. All rights reserved. 3 -26

Figure 3. 54 Copyright © Houghton Mifflin Company. All rights reserved. 3 -27

Guidelines for Solving Applied Minimum and Maximum Problems Copyright © Houghton Mifflin Company. All rights reserved. 3 -28

Newton's Method for Approximating the Zeroes of a Function Copyright © Houghton Mifflin Company. All rights reserved. 3 -29

Definition of Differentials Copyright © Houghton Mifflin Company. All rights reserved. 3 -30

Differential Formulas Copyright © Houghton Mifflin Company. All rights reserved. 3 -31