CHAPTER 3 ANGLE MODULATION FM and PM Signal

CHAPTER 3 ANGLE MODULATION

FM and PM Signal Analysis ü Frequency modulation (FM) and phase modulation (PM) are both forms of angle modulation. Angle modulation results whenever the phase angle ( ) of a sinusoidal wave is varied with respect to time. ü Mathematically, an angle-modulated wave can be expressed by, ü (3. 1) Where = angle-modulated wave = peak carrier amplitude (volts) = carrier radian frequency (rad/sec) = instantaneous phase deviation (rad)

FM Signal Analysis ü Frequency modulation : the process of varying the frequency of a carrier wave in proportion to a modulating signal. ü The amplitude of the carrier is kept constant while its frequency and rate of change are varied by the modulating signal.

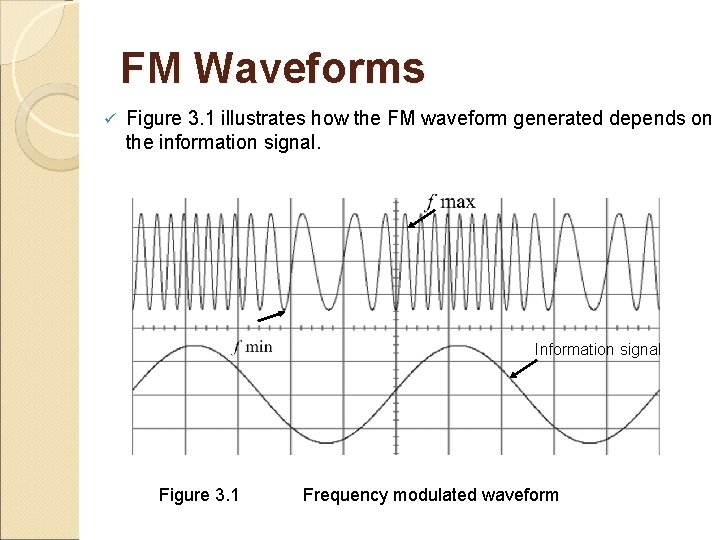
FM Waveforms ü Figure 3. 1 illustrates how the FM waveform generated depends on the information signal. Information signal Figure 3. 1 Frequency modulated waveform

FM Waveforms ü ü When the information signal is at the maximum negative and maximum positive amplitude, the FM signal is at its minimum frequency and maximum frequency, respectively. The important features about FM waveforms are: i) The frequency varies. ii) The rate of change of carrier frequency is the same as the frequency of the information signal. iii) The amount of carrier frequency change is proportional to the amplitude of the information signal. iv) The amplitude is constant.

Deviation Sensitivity ü For a modulating signal , modulation are phase modulation, frequency modulation, the phase and frequency (3. 2) (3. 3) where Kp = deviation sensitivity of the phase modulator (in rad/V ) Kf = deviation sensitivity of the frequency modulator (in rad/sec/volt) Deviation sensitivity : output-versus-input transfer function for the modulators. It gives the relationship between what output parameter changes in respect to specified changes in the input signal. ü Deviation sensitivity for PM : ü

Deviation sensitivity (cont’d) ü Deviation sensitivity for FM : ü Phase modulation is the first integral of frequency modulation. Therefore, from equations (3. 2) and (3. 3), Phase modulation, (3. 4)

Deviation Sensitivity Substitute a modulating signal, equations (3. 2) and (3. 3) yields, into For phase modulation, or (3. 5) For frequency modulation, (3. 6)

Deviation Sensitivity Table 3. 1 : Equations for Phase and Frequency Modulated Carriers

FM Modulation index ü For a frequency-modulated carrier, (3. 8) ü The modulation index, ; if Kf in rad/sec/volt ; if Kf in Hz/ volt Where = modulation index for FM = deviation sensitivity (rad/sec/volt) = peak modulating-signal amplitude (volt) = radian frequency (rad/sec) = angular frequency (Hz) or (3. 9)

FM Modulation index Based on Eq. 3. 9, for an FM carrier, the modulation index is directly proportional to the amplitude of modulating signal & inversely proportional to the frequency of modulating signal.

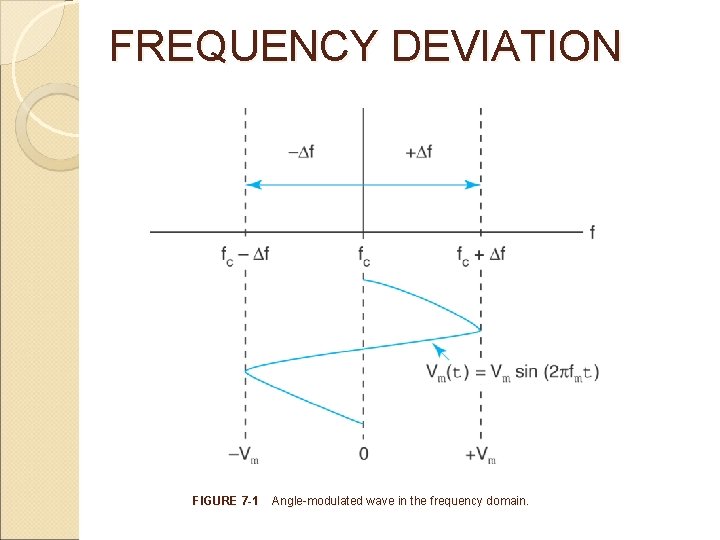
Frequency Deviation Frequency deviation is the change in frequency that occurs in the carrier when it is acted on by a modulating-signal. Frequency deviation, ; Kf in Hz/V (3. 9) modulation index for FM can be rewritten as: The peak-to-peak frequency deviation is called carrier swing, where: Carrier swing, (3. 10)

FREQUENCY DEVIATION FIGURE 7 -1 Angle-modulated wave in the frequency domain.

Frequency Deviation Example 3. 1: Determine the peak frequency deviation and modulation index for an FM modulator with deviation sensitivity when a modulating signal is applied. Solution: Frequency deviation, Modulation index,

Example 3. 2: For a given input signal, an FM broadcast –band transmitter has a frequency deviation, . Determine the frequency deviation if the amplitude of the modulating signal increases by a factor of 2. 5. Solution : Frequency deviation, If Vm increase by a factor of 2. 5, 2. 5 Therefore; also increase by a factor of

Frequency Analysis of Anglemodulated Waves As obtained in equation (3. 8), the FM modulated signal is, Applying Bessel function identities, Where is the Bessel function of the first kind of nth order with argument m: (3. 11) Expanding the above equation, (3. 12)

Frequency Analysis of Anglemodulated Waves Where = angle-modulated wave = modulation index = peak modulating-signal amplitude = carrier component = first set of side frequencies displaced from the carrier by = second set of side frequencies displaced from the carrier by = nth set of side frequencies displaced from the carrier by

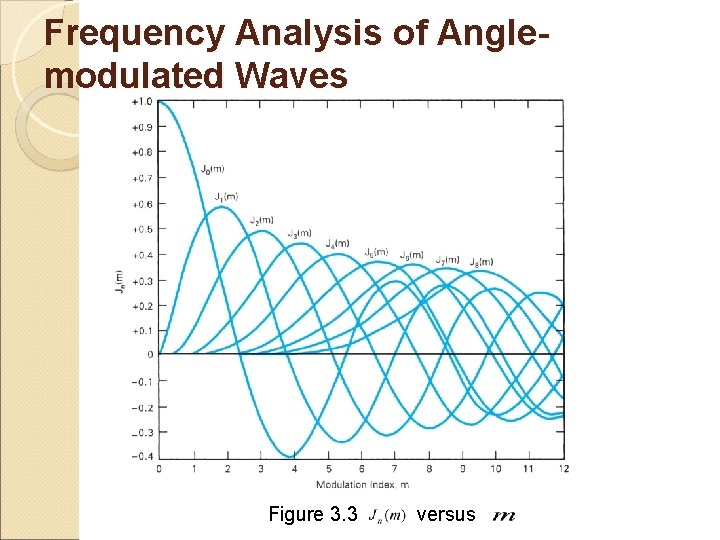
Frequency Analysis of Anglemodulated Waves Notes: 1) Equations (3. 11) and (3. 12) show that with angle modulation, a single-frequency modulating signal produces an infinite number of sets of side frequencies. 2) An important characteristic of Bessel function is, 3) 4) Actual amplitude for the sideband = 5) Relative amplitude for the sideband = (volt) (unitless) or

Frequency Analysis of Anglemodulated Waves Figure 3. 3 versus

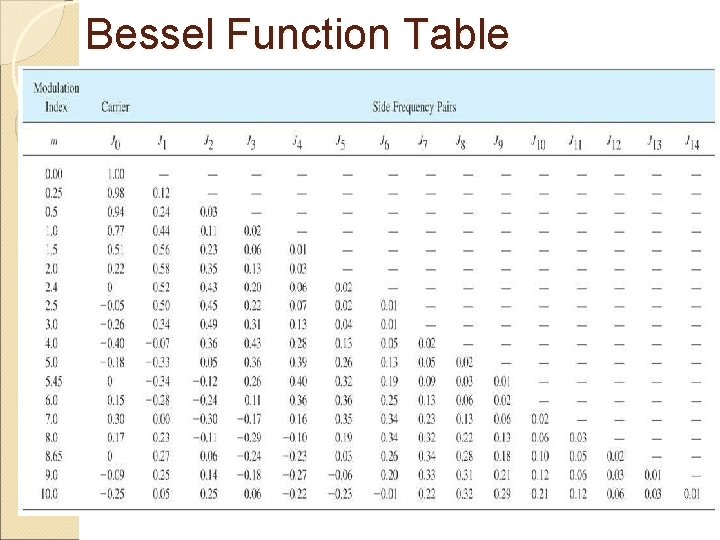
Frequency Analysis of Anglemodulated Waves A side frequency is not considered significant unless it has amplitude equal to or greater than 1% of the unmodulated carrier amplitude. From table, it can be seen that as m increases, the number of significant sideband increase. The modulation index, determines the number of significant sidebands, their amplitudes, and the amplitude of the carrier. Table 3. 1 illustrates that the number of pairs of sidebands generated depend on the values of the modulation index,

Bessel Function Table

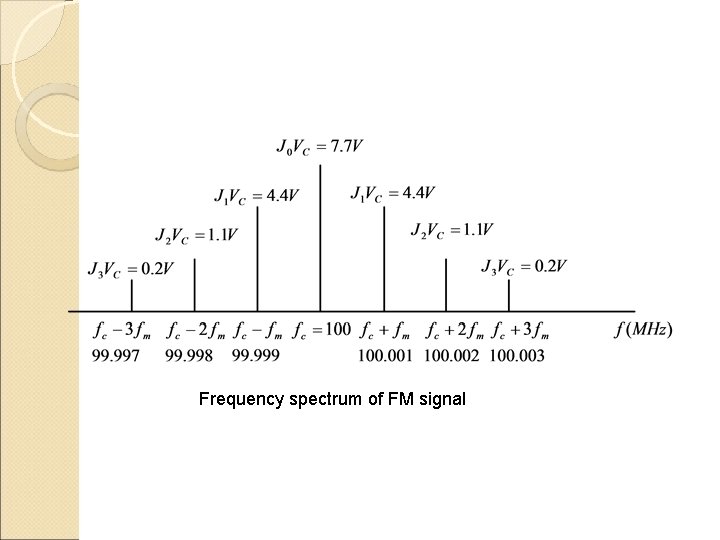
Example 3. 3: For an FM modulator with a modulation index of 1, a modulating signal and an unmodulated carrier , determine the : i) number of sets of significant sidebands, ii) amplitude of the sidebands, Sketch and label the frequency spectrum showing their actual amplitudes. Solution: From Bessel Function table, when mf equals to 1, the number of significant sidebands, n is 3. The amplitudes of the sidebands are as shown in the figure below

Frequency spectrum of FM signal

Example 3. 4 A transmission signal of an audio signal is given by. With the aid of a Bessel Function table, determine: i. the frequency deviation ( f) and the carrier swing (fcs) ii. The maximum and the minimum frequencies iii. the number of set significant sideband. Sketch the frequency spectrum of the FM signal.

Bandwidth Requirement for Angle-modulated Waves The Bessel Table Theoretically, an FM signal contains an infinite number of sidebands, so that the bandwidth required to transmit such a signal is similarly infinite in extent. Practically, significant sidebands are limited, depending on the value of mf. A sideband is considered significant if its relative amplitude is greater or equal to 1%. Using Bessel function table from Table 3. 1, the bandwidth is given by: (3. 13) Where, = number of pairs of the significant sidebands = modulating signal frequency (Hz)

Bandwidth Requirement for Angle-modulated Waves Carson’s Rule Carson’s rule approximates the bandwidth that includes approximately 98% of the total power in the modulated wave It is a rule of thumb that states that, the bandwidth required to pass an FM wave is twice the sum of the deviation and the highest modulating frequency. It is only accurate if the modulation index is higher that about 6. Mathematically stated, Carson’s rule is, (3. 14) Where = peak frequency deviation (Hz) = modulating signal frequency (Hz) Carson’s rule is an approximation and gives transmission bandwidths that are slightly narrower than the bandwidths determined using the Bessel table and equation (3. 13)

Example 3. 3: For an FM modulator with a peak frequency deviation, of , a modulating-signal frequency, fm of 10 k. Hz, Vc is 10 V, and a 100 MHz carrier, determine the: a) actual minimum bandwidth from the Bessel function table, b) approximate minimum bandwidth using Carson’s rule Solution: a) Modulation index, From Bessel function table, at mf equals to 7. 5, the number of significant sidebands, n is 11. Solving, b) From equation (3. 14), using Carson’s rule,

DEVIATION RATIO Deviation ratio : the worst-case modulation index and is equal to the maximum peak frequency deviation divided by the maximum modulating signal frequency. Mathematically ; Where : DR=deviation ratio (unitless) = maximum peak frequency deviation (Hz) = maximum modulating signal frequency (Hz) The worst case modulation index produces the widest output frequency spectrum.

DEVIATION RATIO Example 3. 4 a) Determine the deviation ratio and the bandwidth for the worst-case (widest bandwidth) modulation index for an FM broadcast-band transmitter with a maximum frequency deviation of 75 k. Hz and a maximum modulating signal frequency of 15 k. Hz. b) Determine the deviation ratio and maximum bandwidth for an equal modulation index with only half the peak frequency deviation and modulating signal frequency.

FM POWER DISTRIBUTION As seen in Bessel Function Table, it shows that as the sideband relative amplitude increases, the carrier amplitude , J 0 decreases. This is because in FM, the total transmitted power is always constant and the total average power is equal to the unmodulated carrier power, that is the amplitude of the FM remains constant whether or not it is modulated. In effect, in FM, the total power that is originally in the carrier is redistributed between all components of the spectrum, in an amount determined by the modulation index, mf and the corresponding Bessel Function. At certain value of modulation index, the carrier component goes to zero, where in this condition the power is carried by the sidebands only.

FM POWER DISTRIBUTION The average power in angle modulated wave is equal to the power of the unmodulated carrier : The total instantaneous power in the angle modulated carrier:

FM POWER DISTRIBUTION The total modulated power : Where = total power (watts) = modulated carrier power (watts) = power in the first set of sidebands (watts) = power in the second set of sidebands (watts) = power in the nth set of sidebands (watts)

FM POWER DISTRIBUTION Example 3. 5 For an FM modulator with a modulation index m = 1, a modulating signal , vm(t) = Vmsin(2π1000 t) and an unmodulated carrier, vc(t) = 10 sin(2π500 kt). Determine the unmodulated carrier power for the FM modulator given with a load resistance, RL = 50Ω. Determine also the total power in the angle-modulated wave.

Solution: Unmodulated carrier power: Total power in the angle-modulated wave:

EXERCISE A Frequency Modulation (FM) modulator has a frequency deviation of 20 k. Hz. If a 10 V, 100 MHz carrier is modulated by a signal of 4 k. Hz, write the trigonometric equation of the instantaneous FM voltage.

EXERCISE A 107. 6 MHz carrier is frequency modulated by a 7 k. Hz sine wave. The resultant FM signal has a frequency deviation of 50 k. Hz. a) Find the carrier swing of the FM signal b) Determine the highest and lowest frequencies attained by the modulated signal. c) Calculate the modulation index of the FM wave.

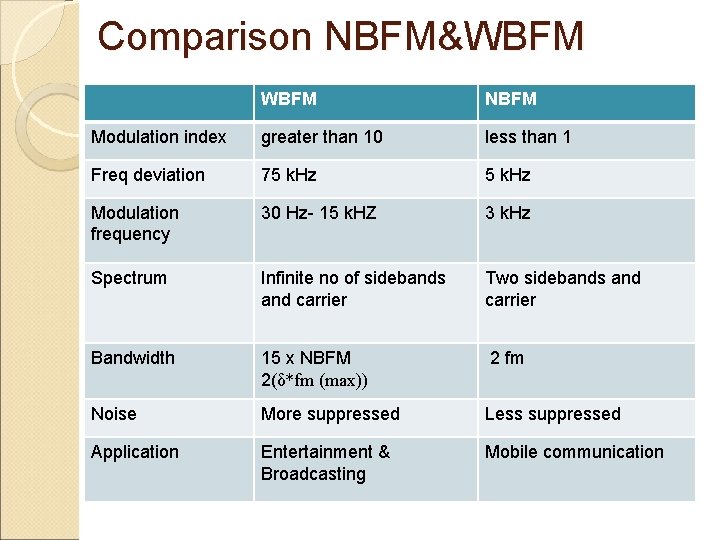
Comparison NBFM&WBFM NBFM Modulation index greater than 10 less than 1 Freq deviation 75 k. Hz Modulation frequency 30 Hz- 15 k. HZ 3 k. Hz Spectrum Infinite no of sidebands and carrier Two sidebands and carrier Bandwidth 15 x NBFM 2(δ*fm (max)) 2 fm Noise More suppressed Less suppressed Application Entertainment & Broadcasting Mobile communication

Phase Modulation (PM) Signal Analysis Phase modulation is a system in which the phase of the carrier signal is varied by the information signal. ü The amplitude of the carrier signal is kept constant. ü The phase ( ) in the equation 3. 1 is varied so that its magnitude is proportional to instantaneous amplitude of the modulating signal. ü

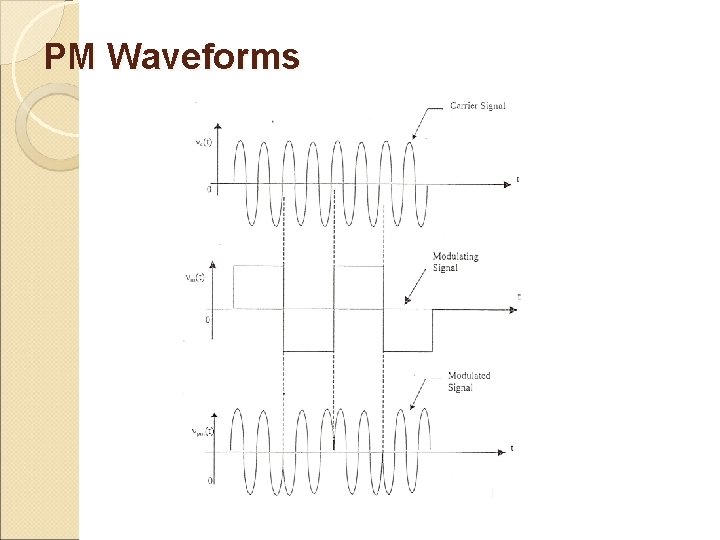
PM Waveforms ü Figure 3. 2 illustrates how the PM waveform generated depends on the phase change of the information signal. It is best illustrated using a square information signal or modulating signal.

PM Waveforms

Phase Deviation and Modulation index ü For a carrier that is being phase modulated, it can be expressed by, (3. 7) ü The modulation index for a phase-modulated carrier is expressed mathematically as, Where = modulation index for PM or peak phase deviation(= ) = deviation sensitivity = peak modulating-signal amplitude (volt)

Example : Determine the peak phase deviation (m) for a PM modulator with a deviation sensitivity K = 2. 5 rad/V and a modulating signal, Solution: Peak phase deviation for PM wave is the modulation index.

TABLE 7 -2 Summary Angle Modulation