Chapter 3 4 Euclidean General Vector Spaces MATH

















































- Slides: 50

Chapter 3 - 4 = Euclidean & General Vector Spaces MATH 264 Linear Algebra

Introduction

Continued on Next Slide

Vectors in 2 -space, 3 space, and n-space Section 3. 1 in Textbook

Definitions Vectors with the same length and direction are said to be equivalent. The vector whose initial and terminal points coincide has length zero so we call this the zero vector and denote it as 0. The zero vector has no natural direction therefore we can assign any direction that is convenient to us for the problem at hand.





Subspaces Section 4. 2 in Textbook

Intro to Subspaces It is often the case that some vector space of interest is contained within a larger vector space whose properties are known. In this section we will show to recognize when this is the case, we will explain how the properties of the larger vector space can be used to obtain properties of the smaller vector space, and we will give a variety of important examples.

Definition: A subset W of vector space V is called a subspace of V if W is itself a vector space under the addition and scalar multiplication defined on V.


Theorem 4. 2. 1 If W is a set of one or more vectors in a vector space V then W is a subspace of V if and only if the following conditions are true: If u and v are vectors in W then u+v is in W b) If k is a scalar and u is a vector in W then ku is in W a) This theorem states that W is a subspace of V if and only if it’s closed under addition and scalar multiplication.




Theorem 4. 2. 2: Definition:

Theorem 4. 2. 3:


Example:

Linear Independence Section 4. 3 in Textbook

Intro to Linear Independence


Theorem:


Example: Continued on Next Slide



Example:

Continued on Next Slide

Continued on Next Slide



Coordinates & Basis Section 4. 4 in Textbook

Intro to Section 4. 4 Ø We usually think of a line as being one-dimensional, a plane as two-dimensional, and the space around us as three-dimensional. Ø It is the primary goal of this section and the next to make this intuitive notion of dimension precise. Ø In this section we will discuss coordinate systems in general vector spaces and lay the groundwork for a precise definition of dimension in the next section.


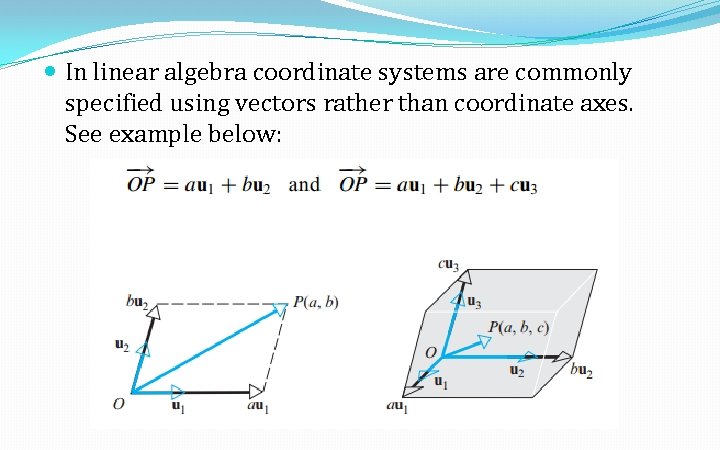
In linear algebra coordinate systems are commonly specified using vectors rather than coordinate axes. See example below:

Units of Measurement They are essential ingredients of any coordinate system. In geometry problems one tries to use the same unit of measurement on all axes to avoid distorting the shapes of figures. This is less important in application









Questions to Get Done Suggested practice problems 1 ( 1 th edition) Section 3. 1 #1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23 Section 3. 2 #1, 3, 5, 7, 9, 11 Section 3. 3 #1, 13, 15, 17, 19 Section 3. 4 #17, 19, 25

Questions to Get Done Suggested practice problems 1 ( 1 th edition) Section 4. 2 #1, 7, 11 Section 4. 3 #3, 9, 11 Section 4. 4 #1, 7, 11, 13 Section 4. 5 #1, 3, 5, 13, 15, 17, 19 Section 4. 7 #1 -19 (only odd) Section 4. 8 #1, 3, 5, 7, 9, 15, 19, 21

Questions to Get Done Suggested practice problems 1 ( 1 th edition) Section 6. 2 #1, 7, 25, 27
 Vector space matrix
Vector space matrix Dimensions of a vector space
Dimensions of a vector space What is a unit vector
What is a unit vector Cosenos directores de un vector
Cosenos directores de un vector Why is vector resolution the opposite of vector addition
Why is vector resolution the opposite of vector addition Define a position vector
Define a position vector Euclid algorithm
Euclid algorithm Grade 11 circle geometry theorems
Grade 11 circle geometry theorems Flat clustering vs hierarchical clustering
Flat clustering vs hierarchical clustering Euclidean algorithm
Euclidean algorithm Bitonic euclidean traveling salesman problem
Bitonic euclidean traveling salesman problem What is euclidean inner product
What is euclidean inner product Euclidean method gcf
Euclidean method gcf Cse 202
Cse 202 Contoh soal euclidean distance
Contoh soal euclidean distance Extended euclidean algorithm
Extended euclidean algorithm Kombinasi lanjar
Kombinasi lanjar Ramsey theory on the integers
Ramsey theory on the integers Fluorocein
Fluorocein Contoh soal euclidean distance
Contoh soal euclidean distance Jarak euclidean
Jarak euclidean Pernyataan 4 x (9-4) = 36 -16 memenuhi sifat….
Pernyataan 4 x (9-4) = 36 -16 memenuhi sifat…. Euclidean transformation
Euclidean transformation Uri klein
Uri klein Euclidean space
Euclidean space Euclidean
Euclidean Geometry
Geometry Hit the button
Hit the button Uil math scoring
Uil math scoring Diferencia entre gran plano general y plano general
Diferencia entre gran plano general y plano general Where did general lee surrender to general grant?
Where did general lee surrender to general grant? New-twinspace.etwinning.net
New-twinspace.etwinning.net Hardened magma squeezed into vertical spaces between rocks
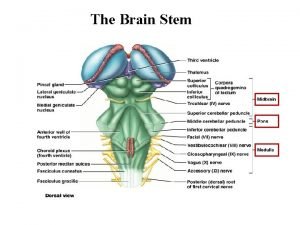
Hardened magma squeezed into vertical spaces between rocks Brain stem
Brain stem Ollies worcester
Ollies worcester Labioversion tooth
Labioversion tooth Spaces of the neck
Spaces of the neck Spaces of parona
Spaces of parona Space of parona boundaries
Space of parona boundaries Predentate period
Predentate period Ros smith
Ros smith Sample complexity for finite hypothesis spaces
Sample complexity for finite hypothesis spaces Class 1 canine relationship
Class 1 canine relationship Alar space
Alar space Vector space properties
Vector space properties Spaces between particles of liquid
Spaces between particles of liquid Performance space definition
Performance space definition Enabling objectives
Enabling objectives Kennedy class 4 mod 2
Kennedy class 4 mod 2 Ancillary spaces
Ancillary spaces Spaces cite multimedia
Spaces cite multimedia