Chapter 3 3 6 Integers and Algorithms Representations

Chapter 3 3. 6 Integers and Algorithms ‒ Representations of integers ‒ Algorithms for integer operations ‒ Modular Exponentiation ‒ The Euclidean Algorithm 1

Representations of integers • Theorem 1: Let b be a positive integer greater than 1. Then if n is a positive integer, it can be expressed uniquely in the form where k is a nonnegative integer, a 0, a 1, …, ak are nonnegative integers less than b, and ak ≠ 0. 2

• Example 1: What is the decimal expansion of the integer that has (1 0101 1111)2 as its binary expansion? • Example 2: What is the decimal expansion of the hexadecimal expansion of (2 AE 0 B)16 ? 3

• Example 3: Find the base 8, or octal, expansion of (12345)10 • Example 4: Find the hexadecimal expansion of (177130)10? 4

• Algorithm 1: Construction Base b Expansions procedure base b expansion(n: positive integer) q: = n k: =0 while q ≠ 0 begin ak : =q mod b q: = k: =k+1 end {the base b expansion of n is (ak-1. . . a 1 a 0)b} 5

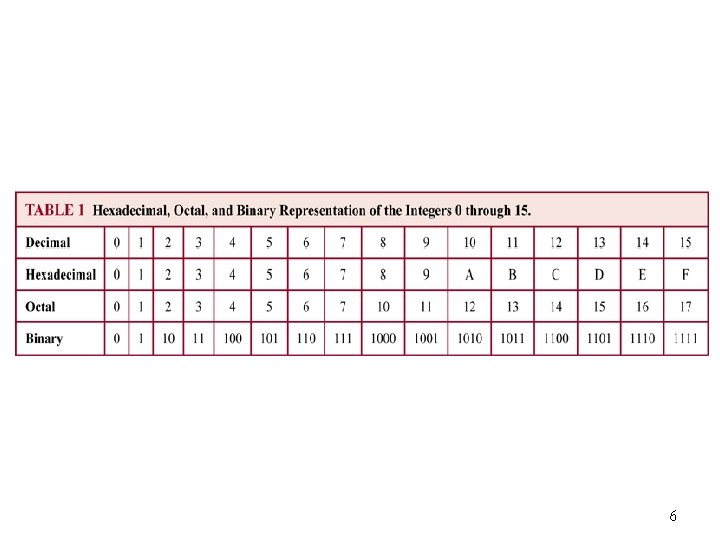
6

Algorithms for integer operations • Algorithm 2: Addition of Integers Procedure add(a , b: positive integers) {the binary expansions of a and b are (an-1. . . a 1 a 0)2 and (bn-1. . . b 1 b 0)2 respectively} c : =0 for j: =0 to n-1 Begin d: = sj : = aj+bj+c-2 d c : =d end sn: =c {the binary expansion of the sum if (sn sn-1. . . s 1 s 0)2 } 7

Algorithms for integer operations Example 7: Add a=(1110)2 and b=(1011)2. 8

Algorithms for integer operations • Algorithm 3 : Multiplying Integers procedure multiply(a, b : positive integers) {the binary expansions of and b are(an-1. . . a 1 a 0)2 and (bn-1. . . b 1 b 0)2 respectively} for j: =0 to n-1 Begin if bj =1 then cj=a shifted j places else cj: =0 end {c 0 c 1. . . cn-1 are the partial products} p : =0 for j: =0 to n-1 p: = p +cj {p is the value of ab} 9

Algorithms for integer operations Example 9: Find the product of a= (110)2 and b=(101)2 10

Algorithms for integer operations • Algorithm 4 : Computing div and mod procedure division algorithm(a : integers , d: positive integer) q: =0 r: =|a| while r≧d begin r : = r-d q : =q+1 end if a<0 then if r=0 then q: =-q else begin r : = d-r q : = -(q+1) end {q = a div d is the quotient, r = a mod d is the remainder} 11

Modular Exponentiation • In cryptography it is important to be able to find bn mod m efficiently, where b, n and m and large integers. It’s impractical to first compute bn and then find its remainder when divided by m because bn will be a huge number. Instead, we can use an algorithm that employ expansion of the exponent n , say n = (ak-1. . . a 1 a 0)2. • Before we present this algorithm, we illustrate its basic idea. We will explain how to use the binary expansion of n to compute bn. First , note that 12

Modular Exponentiation • To compute bn , we find the values of b, b 2, (b 2)2=b 4, (b 4)2=b 8, . . . , . • We multiply the terms This gives us in this list, where aj=1. . • For example, to compute 311 we first note that 11 = (1011)2, so that 311= 383231. • By successively squaring, we find that 32=9, 34=81, 38=6561. • Consequently, 311=383231=6561*9*3= 177, 147 13

Modular Exponentiation • Algorithm 5: Modular Exponentiation procedure modular exponentiation(b: integer , n=(ak-1. . . a 1 a 0)2 , m: positive integer) x: = 1 Example 11: Use Algorithm 5 power : = b mod m to find 3644 mod 645. for i=0 to k-1 begin if ai =1 then x : =(x*power) mod m power : =(power*power) mod m End {x equals bn mod m} 14

The Euclidean Algorithm • Lemma 1: Let a=bq+r , where a, b, q, and r are integers. Then gcd(a, b)=gcd(b, r). • Algorithm 6: The Euclidean Algorithm procedure gcd(a. b: integers) x: = a y: = b while y 0 begin r : = x mod y x : = y y : = r end {gcd(a, b) is x} 15

The Euclidean Algorithm • Example 12: Find the GCD of 414 and 662 using the Euclidean Algorithm. 16