Chapter 28 Atomic Physics Plum Pudding Model of







































- Slides: 59

Chapter 28 Atomic Physics

Plum Pudding Model of the Atom • J. J. Thomson’s “Plum Pudding” model of the atom: • Electrons embedded throughout the a volume of positive charge • A change from Newton’s model of the atom as a tiny, hard, indestructible sphere Sir Joseph John Thomson 1856 – 1940

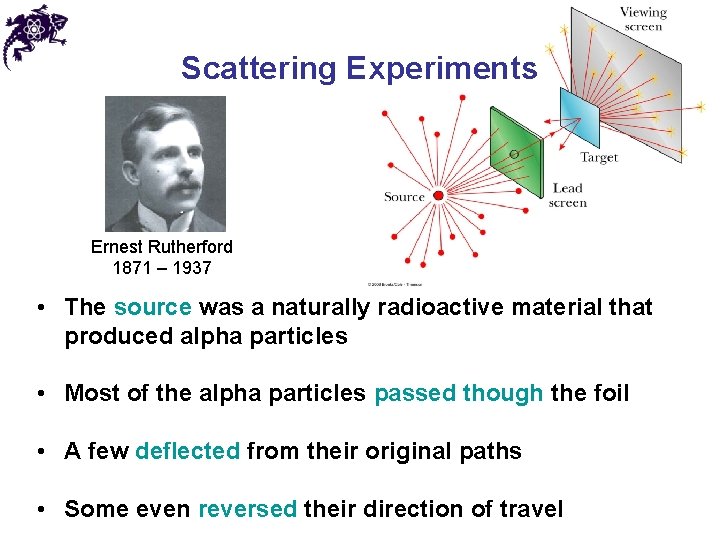
Scattering Experiments Ernest Rutherford 1871 – 1937 • The source was a naturally radioactive material that produced alpha particles • Most of the alpha particles passed though the foil • A few deflected from their original paths • Some even reversed their direction of travel

Planetary Model of the Atom • Based on results of thin foil scattering experiments, Rutherford’s Planetary model of the atom: • Positive charge is concentrated in the center of the atom, called the nucleus • Electrons orbit the nucleus like planets orbit the sun

Chapter 28 Problem 6 In a Rutherford scattering experiment, an α-particle (charge = +2 e) heads directly toward a gold nucleus (charge = +79 e). The α-particle had a kinetic energy of 5. 0 Me. V when very far (r → ∞) from the nucleus. Assuming the gold nucleus to be fixed in space, determine the distance of closest approach.

Difficulties with the Rutherford Model • Atoms emit certain discrete characteristic frequencies of electromagnetic radiation but the Rutherford model is unable to explain this phenomena • Rutherford’s electrons are undergoing a centripetal acceleration and so should radiate electromagnetic waves of the same frequency • The radius should steadily decrease as this radiation is given off • The electron should eventually spiral into the nucleus, but it doesn’t

Emission Spectra • A gas at low pressure and a voltage applied to it emits light characteristic of the gas • When the emitted light is analyzed with a spectrometer, a series of discrete bright lines –emission spectrum – is observed • Each line has a different wavelength and color

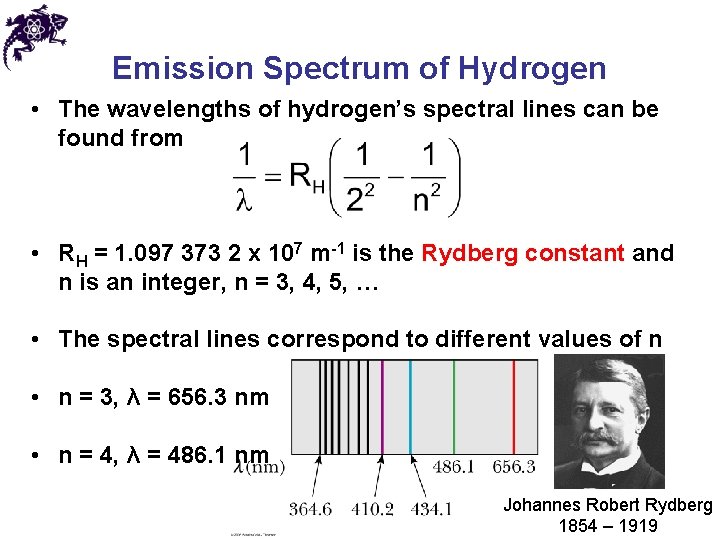
Emission Spectrum of Hydrogen • The wavelengths of hydrogen’s spectral lines can be found from • RH = 1. 097 373 2 x 107 m-1 is the Rydberg constant and n is an integer, n = 3, 4, 5, … • The spectral lines correspond to different values of n • n = 3, λ = 656. 3 nm • n = 4, λ = 486. 1 nm Johannes Robert Rydberg 1854 – 1919

Absorption Spectra • An element can also absorb light at specific wavelengths • An absorption spectrum can be obtained by passing a continuous radiation spectrum through a vapor of the gas • Such spectrum consists of a series of dark lines superimposed on the otherwise continuous spectrum • The dark lines of the absorption spectrum coincide with the bright lines of the emission spectrum

The Bohr Theory of Hydrogen • In 1913 Bohr provided an explanation of atomic spectra that includes some features of the currently accepted theory • His model was an attempt to explain why the atom was stable and included both classical and non-classical ideas Niels Henrik David Bohr 1885 – 1962

The Bohr Theory of Hydrogen • The electron moves in circular orbits around the proton under the influence of the Coulomb force of attraction, which produces the centripetal acceleration • Only certain electron orbits are stable • In these orbits electrons do not emit energy in the form of electromagnetic radiation • Therefore, the energy of the atom remains constant and classical mechanics can be used to describe the electron’s motion

The Bohr Theory of Hydrogen • Radiation is emitted when the electrons “jump” (not in a classical sense) from a more energetic initial state to a lower state • The frequency emitted in the “jump” is related to the change in the atom’s energy: Ei – Ef = h ƒ • The size of the allowed electron orbits is determined by a quantization condition imposed on the electron’s orbital angular momentum: me v r = n ħ where n = 1, 2, 3, …; ħ = h / 2 π

Radii and Energies of Orbits

Radii and Energies of Orbits

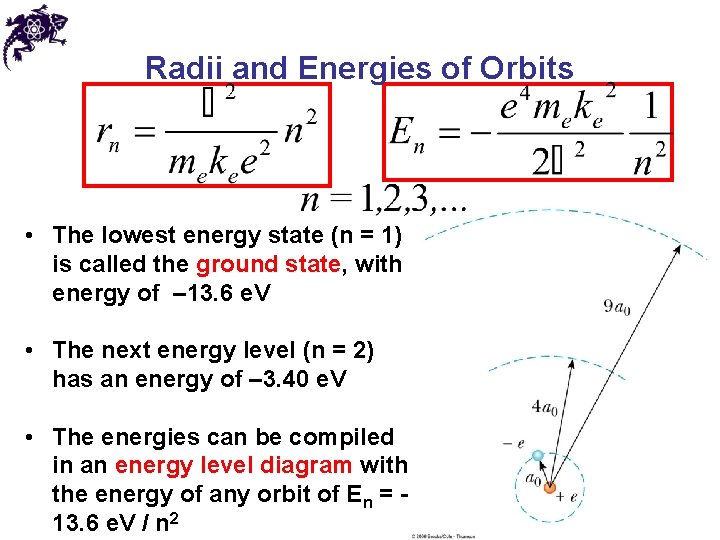
Radii and Energies of Orbits • The radii of the Bohr orbits are quantized • When n = 1, the orbit has the smallest radius, called the Bohr radius, ao = 0. 0529 nm • A general expression for the radius of any orbit in a hydrogen atom is rn = n 2 ao

Radii and Energies of Orbits • The lowest energy state (n = 1) is called the ground state, with energy of – 13. 6 e. V • The next energy level (n = 2) has an energy of – 3. 40 e. V • The energies can be compiled in an energy level diagram with the energy of any orbit of En = 13. 6 e. V / n 2

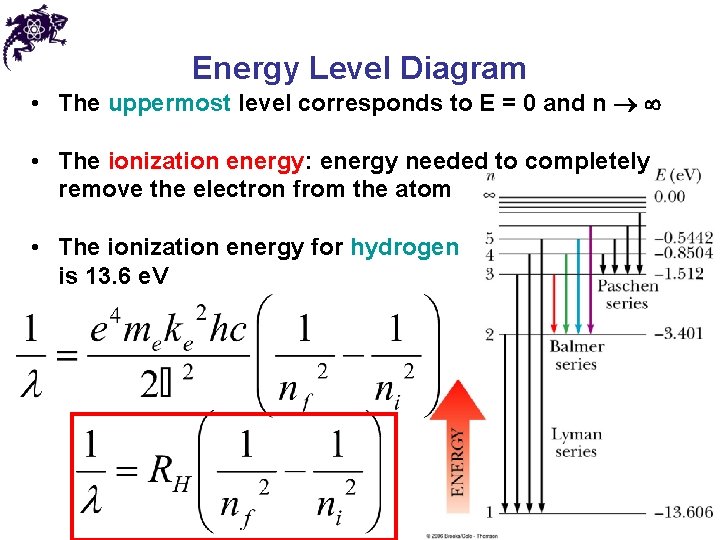
Energy Level Diagram

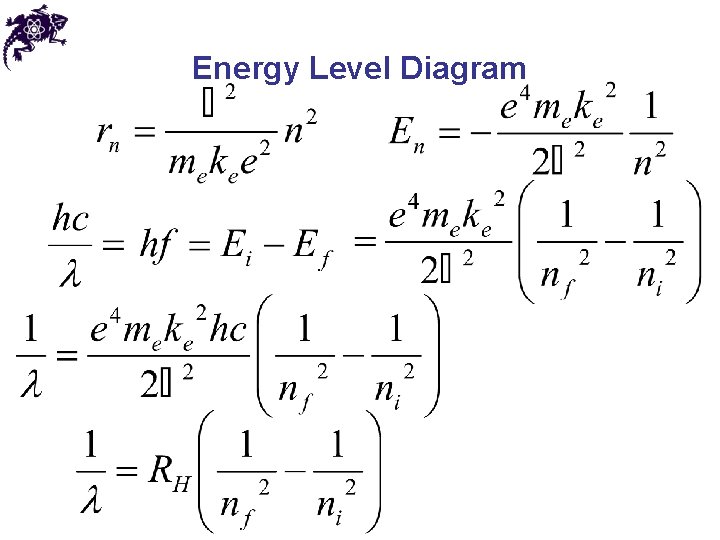
Energy Level Diagram • The value of RH from Bohr’s analysis is in excellent agreement with the experimental value of the Rydberg constant • A more generalized equation can be used to find the wavelengths of any spectral lines

Energy Level Diagram • The uppermost level corresponds to E = 0 and n • The ionization energy: energy needed to completely remove the electron from the atom • The ionization energy for hydrogen is 13. 6 e. V

Chapter 28 Problem 18 A particle of charge q and mass m, moving with a constant speed v, perpendicular to a constant magnetic field, B, follows a circular path. If in this case the angular momentum about the center of this circle is quantized so that mvr = 2 nħ, show that the expression for the allowed radii for the particle is written in the corner, where n = 1, 2, 3, . . .

Chapter 28 Problem 24 Two hydrogen atoms collide head-on and end up with zero kinetic energy. Each then emits a 121. 6 -nm photon (n = 2 to n = 1 transition). At what speed were the atoms moving before the collision?

Modifications of the Bohr Theory – Elliptical Orbits • Sommerfeld extended the results to include elliptical orbits • Retained the principle quantum number, n, which determines the energy of the allowed states • Added the orbital quantum number, ℓ, ranging from 0 to n-1 in integer steps • All states with the same principle quantum number are said to form a shell, whereas the states with given values of n and ℓ are said Arnold Johannes to form a subshell Wilhelm Sommerfeld 1868 – 1951

Modifications of the Bohr Theory – Elliptical Orbits Arnold Johannes Wilhelm Sommerfeld 1868 – 1951

Modifications of the Bohr Theory – Zeeman Effect • Another modification was needed to account for the Zeeman effect: splitting of spectral lines in a strong magnetic field, indicating that the energy of an electron is slightly modified when the atom is immersed in a magnetic field • A new quantum number, m ℓ, called the orbital magnetic quantum number, had to be introduced • m ℓ can vary from - ℓ to + ℓ in integer steps Pieter Zeeman 1865 – 1943

Quantum Number Summary • The values of n can range from 1 to in integer steps • The values of ℓ can range from 0 to n-1 in integer steps • The values of m ℓ can range from -ℓ to ℓ in integer steps

Modifications of the Bohr Theory – Fine Structure • High resolution spectrometers show that spectral lines are, in fact, two very closely spaced lines, even in the absence of a magnetic field • This splitting is called fine structure • Another quantum number, ms, called the spin magnetic quantum number, was introduced to explain the fine structure

Spin Magnetic Quantum Number • It is convenient to think of the electron as spinning on its axis (the electron is not physically spinning) • There are two directions for the spin: spin up, ms = ½; spin down, ms = - ½ • There is a slight energy difference between the two spins and this accounts for the doublet in some lines • A classical description of electron spin is incorrect: the electron cannot be located precisely in space, thus it cannot be considered to be a spinning solid object

de Broglie Waves in the Hydrogen Atom • One of Bohr’s postulates was the angular momentum of the electron is quantized, but there was no explanation why the restriction occurred • de Broglie assumed that the electron orbit would be stable only if it contained an integral number of electron wavelengths

de Broglie Waves in the Hydrogen Atom • This was the first convincing argument that the wave nature of matter was at the heart of the behavior of atomic systems • By applying wave theory to the electrons in an atom, de Broglie was able to explain the appearance of integers in Bohr’s equations as a natural consequence of standing wave patterns

Quantum Mechanics and the Hydrogen Atom • Schrödinger’s wave equation was subsequently applied to hydrogen and other atomic systems - one of the first great achievements of quantum mechanics • The quantum numbers and the restrictions placed on their values arise directly from the mathematics and not from any assumptions made to make theory agree with experiments

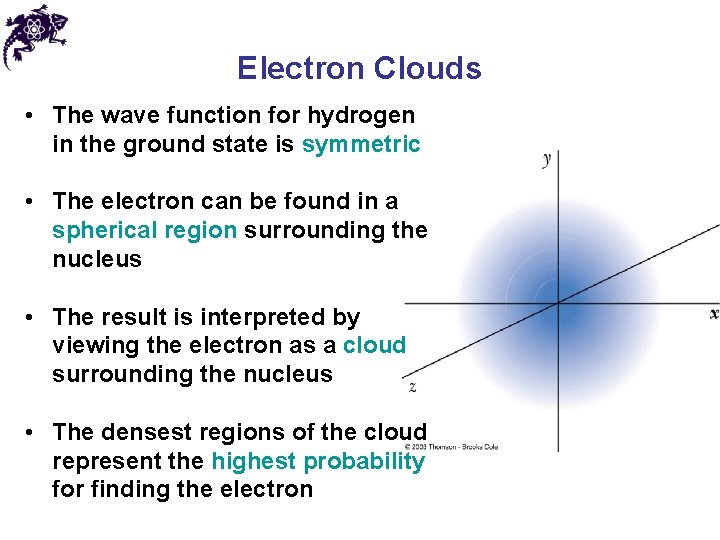
Electron Clouds • The graph shows the solution to the wave equation for hydrogen in the ground state • The curve peaks at the Bohr radius • The electron is not confined to a particular orbital distance from the nucleus • The probability of finding the electron at the Bohr radius is a maximum

Electron Clouds • The wave function for hydrogen in the ground state is symmetric • The electron can be found in a spherical region surrounding the nucleus • The result is interpreted by viewing the electron as a cloud surrounding the nucleus • The densest regions of the cloud represent the highest probability for finding the electron

The Pauli Exclusion Principle • No two electrons in an atom or in the same location can ever have the same set of values of the quantum numbers n, ℓ, m ℓ, and ms • This explains the electronic structure of complex atoms as a succession of filled energy levels with different quantum numbers Wolfgang Ernst Pauli 1900 – 1958

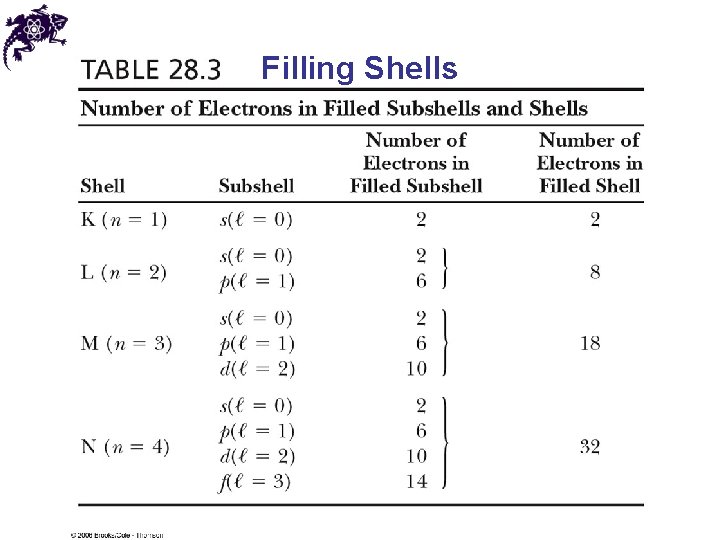
Filling Shells • As a general rule, the order that electrons fill an atom’s subshell is: • 1) Once one subshell is filled, the next electron goes into the vacant subshell that is lowest in energy • 2) Otherwise, the electron would radiate energy until it reached the subshell with the lowest energy • 3) A subshell is filled when it holds 2(2ℓ+1) electrons

Filling Shells

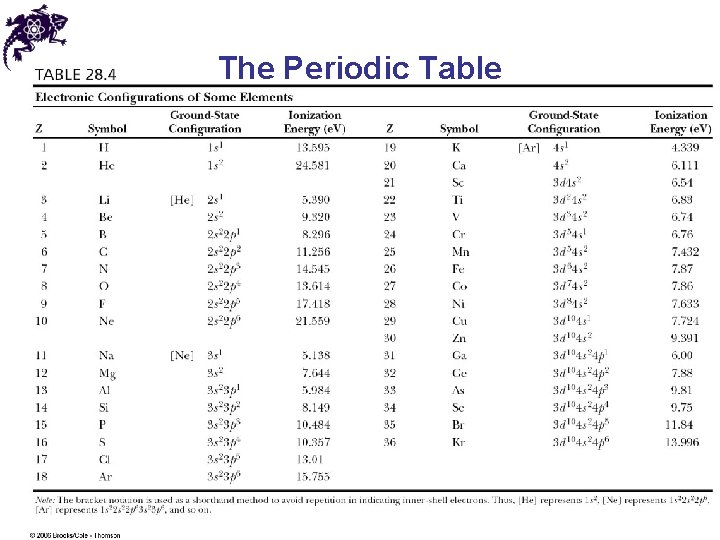
The Periodic Table • The outermost electrons are primarily responsible for the chemical properties of the atom • Mendeleev arranged the elements according to their atomic masses and chemical similarities • The electronic configuration of the elements is explained by quantum numbers and Pauli’s Exclusion Principle Dmitriy Ivanovich Mendeleyev 1834 – 1907

The Periodic Table


Chapter 28 Problem 28 (a) Construct an energy level diagram for the He+ ion, for which Z = 2. (b) What is the ionization energy for He+?

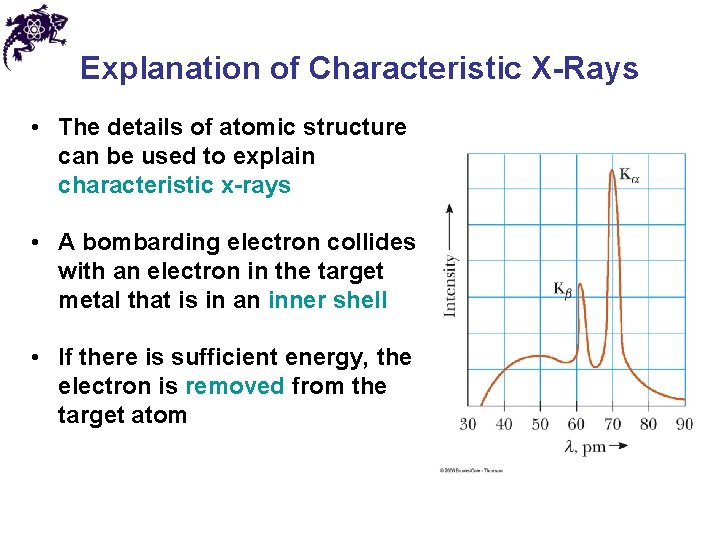
Explanation of Characteristic X-Rays • The details of atomic structure can be used to explain characteristic x-rays • A bombarding electron collides with an electron in the target metal that is in an inner shell • If there is sufficient energy, the electron is removed from the target atom

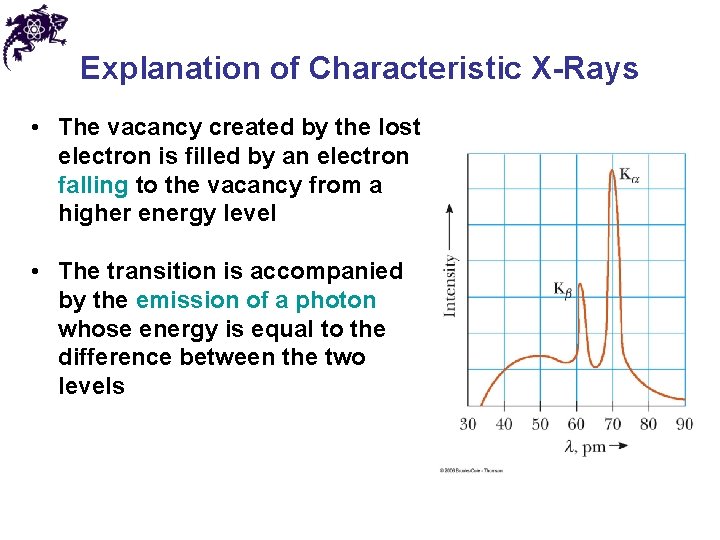
Explanation of Characteristic X-Rays • The vacancy created by the lost electron is filled by an electron falling to the vacancy from a higher energy level • The transition is accompanied by the emission of a photon whose energy is equal to the difference between the two levels

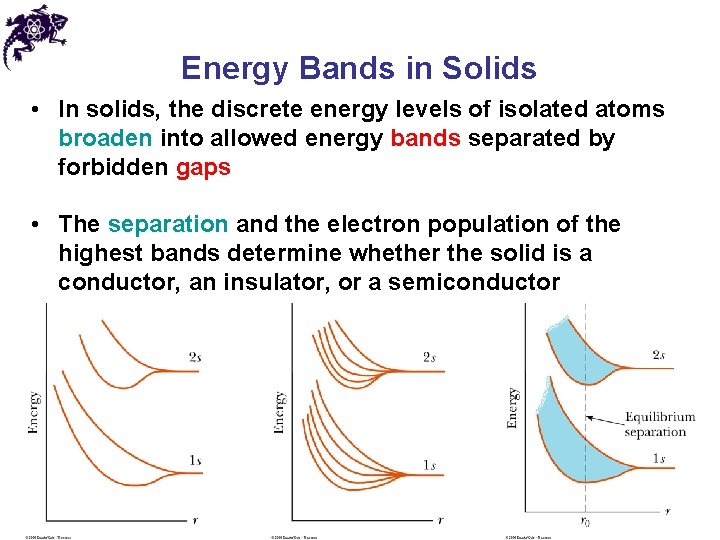
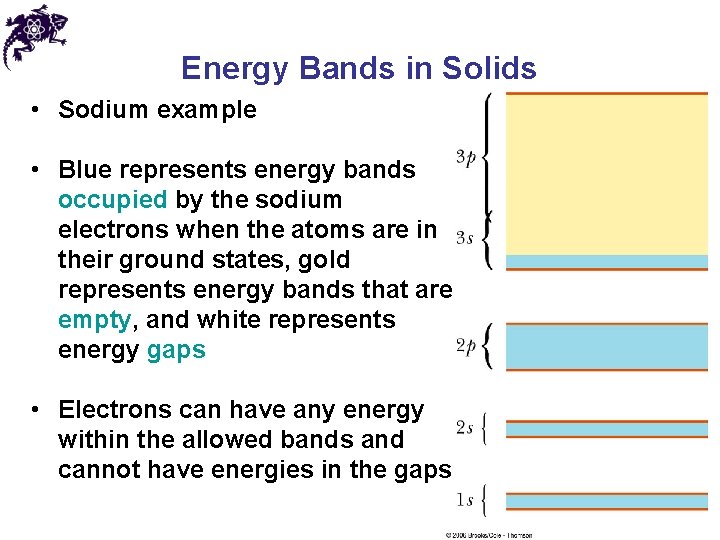
Energy Bands in Solids • In solids, the discrete energy levels of isolated atoms broaden into allowed energy bands separated by forbidden gaps • The separation and the electron population of the highest bands determine whether the solid is a conductor, an insulator, or a semiconductor

Energy Bands in Solids • Sodium example • Blue represents energy bands occupied by the sodium electrons when the atoms are in their ground states, gold represents energy bands that are empty, and white represents energy gaps • Electrons can have any energy within the allowed bands and cannot have energies in the gaps

Energy Level Definitions • The valence band is the highest filled band • The conduction band is the next higher empty band • The energy gap has an energy, Eg, equal to the difference in energy between the top of the valence band the bottom of the conduction band

Conductors • When a voltage is applied to a conductor, the electrons accelerate and gain energy • In quantum terms, electron energies increase if there a high number of unoccupied energy levels for the electron to jump to • For example, it takes very little energy for electrons to jump from the partially filled to one of the nearby empty states

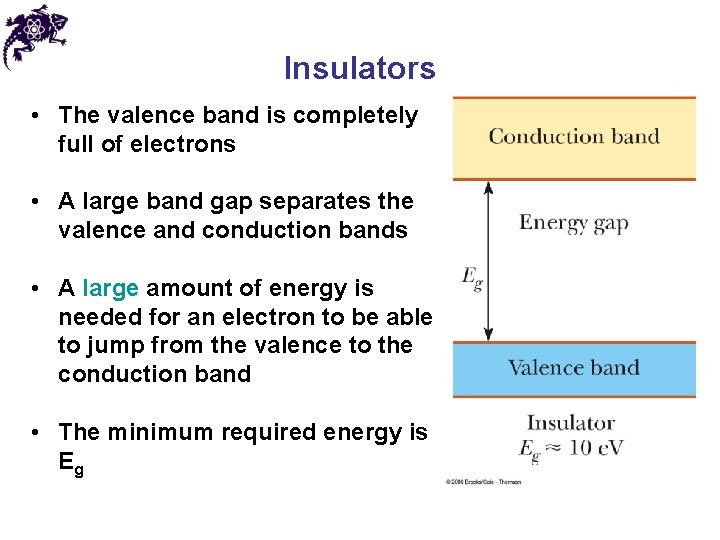
Insulators • The valence band is completely full of electrons • A large band gap separates the valence and conduction bands • A large amount of energy is needed for an electron to be able to jump from the valence to the conduction band • The minimum required energy is Eg

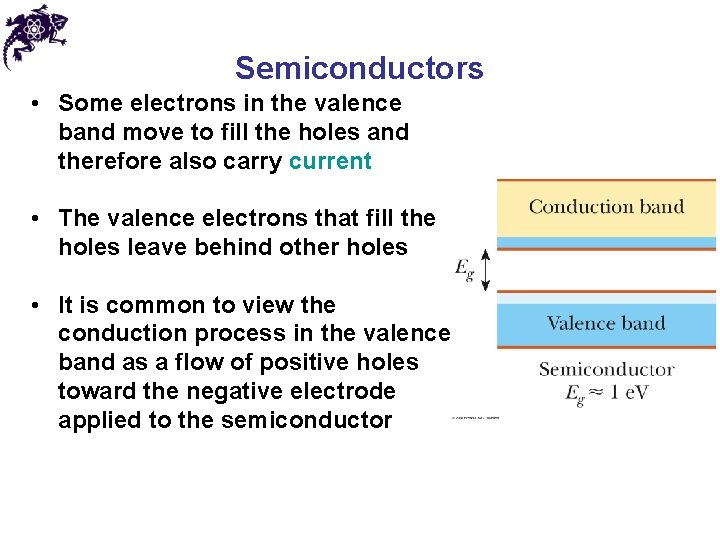
Semiconductors • A semiconductor has a small energy gap • Thermally excited electrons have enough energy to cross the band gap • The resistivity of semiconductors decreases with increases in temperature • The light-color area in the valence band represents holes – empty states in the valence band created by electrons that have jumped to the conduction band

Semiconductors • Some electrons in the valence band move to fill the holes and therefore also carry current • The valence electrons that fill the holes leave behind other holes • It is common to view the conduction process in the valence band as a flow of positive holes toward the negative electrode applied to the semiconductor

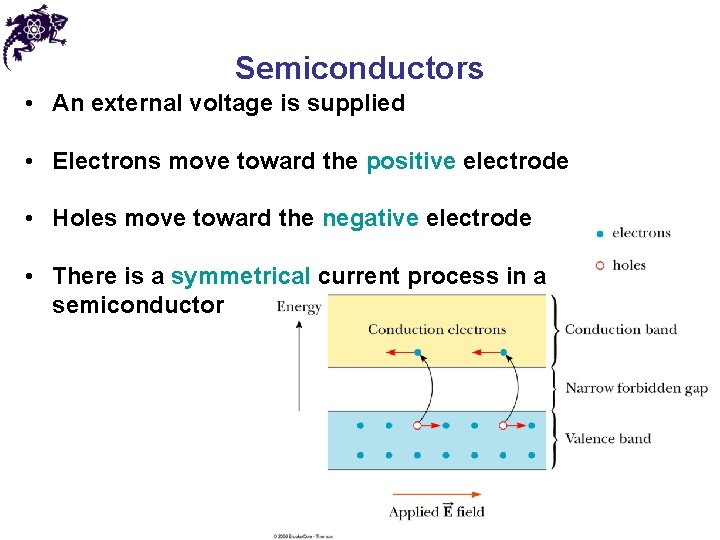
Semiconductors • An external voltage is supplied • Electrons move toward the positive electrode • Holes move toward the negative electrode • There is a symmetrical current process in a semiconductor

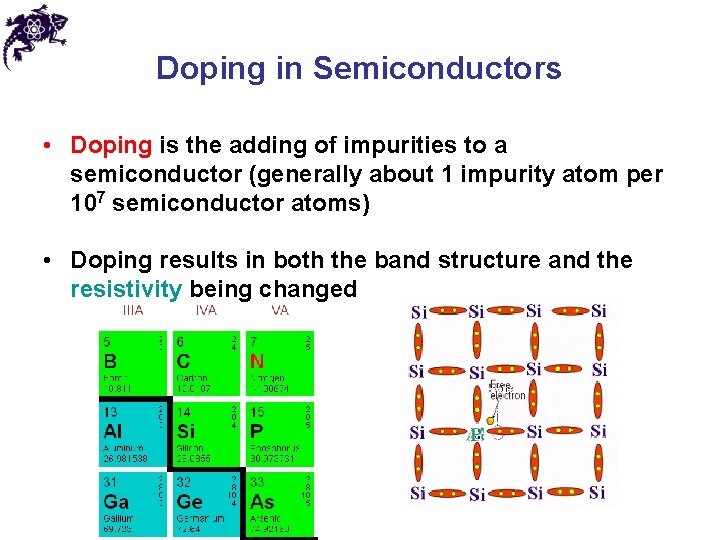
Doping in Semiconductors • Doping is the adding of impurities to a semiconductor (generally about 1 impurity atom per 107 semiconductor atoms) • Doping results in both the band structure and the resistivity being changed

n-type Semiconductors • Donor atoms are doping materials that contain one more electron than the semiconductor material • This creates an essentially free electron with an energy level in the energy gap, just below the conduction band • Only a small amount of thermal energy is needed to cause this electron to move into the conduction band

p-type Semiconductors • Acceptor atoms are doping materials that contain one less electron than the semiconductor material • A hole is left where the missing electron would be • The energy level of the hole lies in the energy gap, just above the valence band • An electron from the valence band has enough thermal energy to fill this impurity level, leaving behind a hole in the valence band

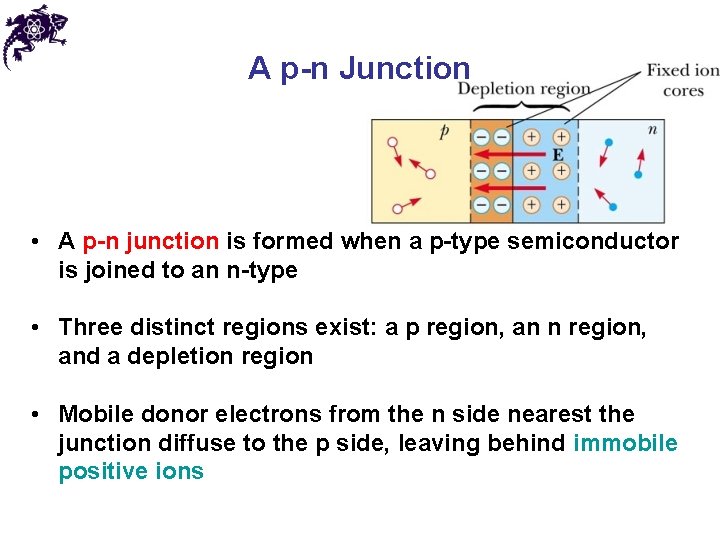
A p-n Junction • A p-n junction is formed when a p-type semiconductor is joined to an n-type • Three distinct regions exist: a p region, an n region, and a depletion region • Mobile donor electrons from the n side nearest the junction diffuse to the p side, leaving behind immobile positive ions

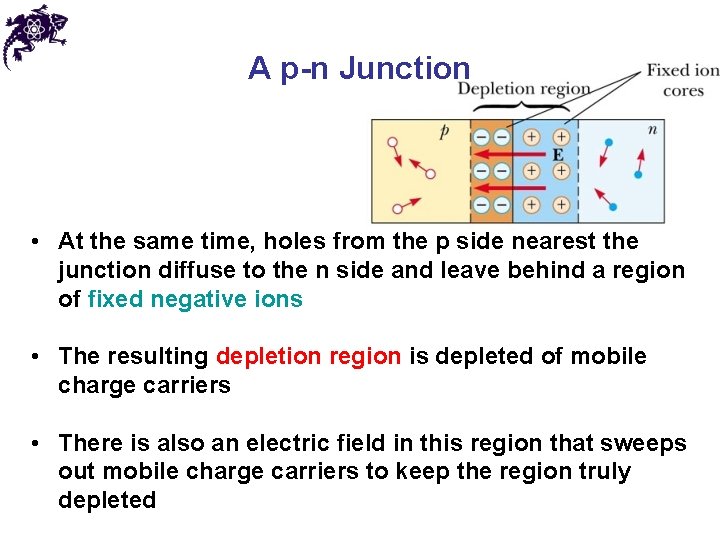
A p-n Junction • At the same time, holes from the p side nearest the junction diffuse to the n side and leave behind a region of fixed negative ions • The resulting depletion region is depleted of mobile charge carriers • There is also an electric field in this region that sweeps out mobile charge carriers to keep the region truly depleted

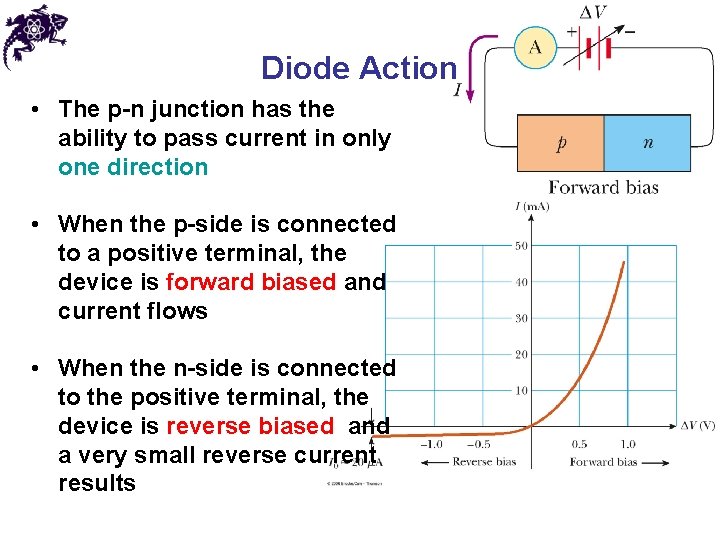
Diode Action • The p-n junction has the ability to pass current in only one direction • When the p-side is connected to a positive terminal, the device is forward biased and current flows • When the n-side is connected to the positive terminal, the device is reverse biased and a very small reverse current results

Answers to Even Numbered Problems Chapter 28: Problem 34 (a) 4 (b) 7

Answers to Even Numbered Problems Chapter 28: Problem 36 Use the lecture notes

Answers to Even Numbered Problems Chapter 28: Problem 44 137

Answers to Even Numbered Problems Chapter 28: Problem 52 (a) 135 e. V (b) ~ 10 times the magnitude of the ground state energy of hydrogen