Chapter 27 Photoelectric Effect WaveParticle Duality Heisenberg Uncertainty

Chapter 27 - Photoelectric Effect - Wave/Particle Duality - Heisenberg Uncertainty Principle

First discovered by Hertz in 1887 (as a side note in an experiment which demonstrated the wave nature of light as hypothesized by Maxwell), the photoelectric effect could only be explained by a particle model of light!

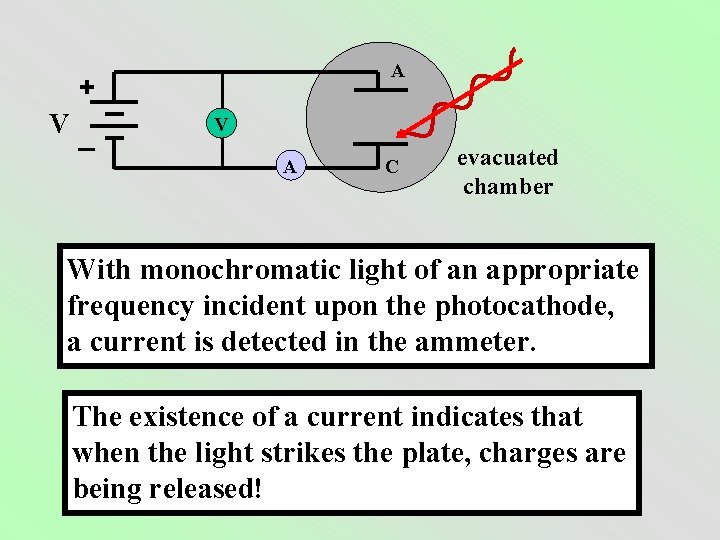
A + V_ V A C evacuated chamber With monochromatic light of an appropriate frequency incident upon the photocathode, a current is detected in the ammeter. The existence of a current indicates that when the light strikes the plate, charges are being released!

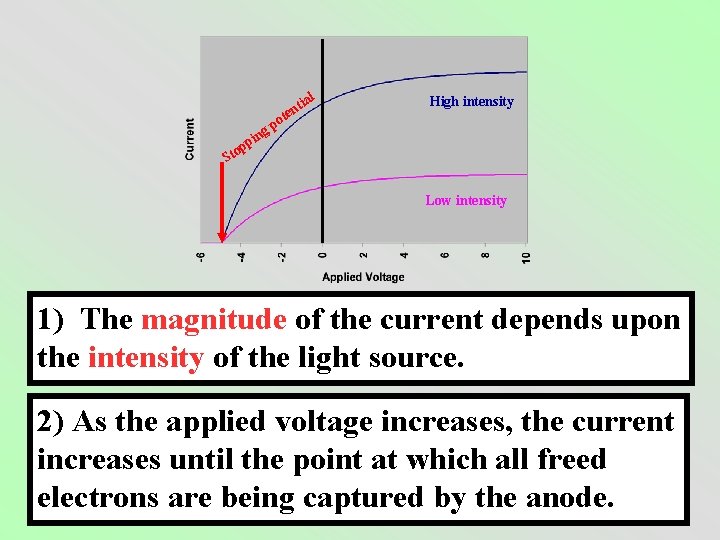
ial t ten High intensity o gp n i p op t S Low intensity 1) The magnitude of the current depends upon the intensity of the light source. 2) As the applied voltage increases, the current increases until the point at which all freed electrons are being captured by the anode.

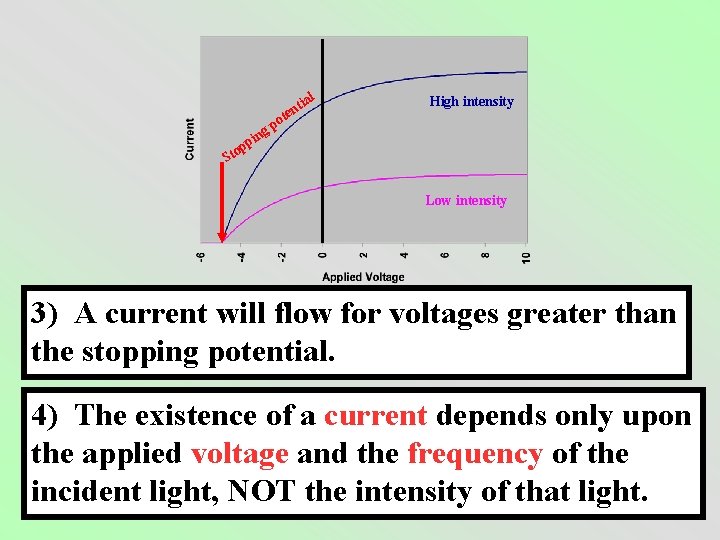
ial t ten High intensity o gp n i p op t S Low intensity 3) A current will flow for voltages greater than the stopping potential. 4) The existence of a current depends only upon the applied voltage and the frequency of the incident light, NOT the intensity of that light.

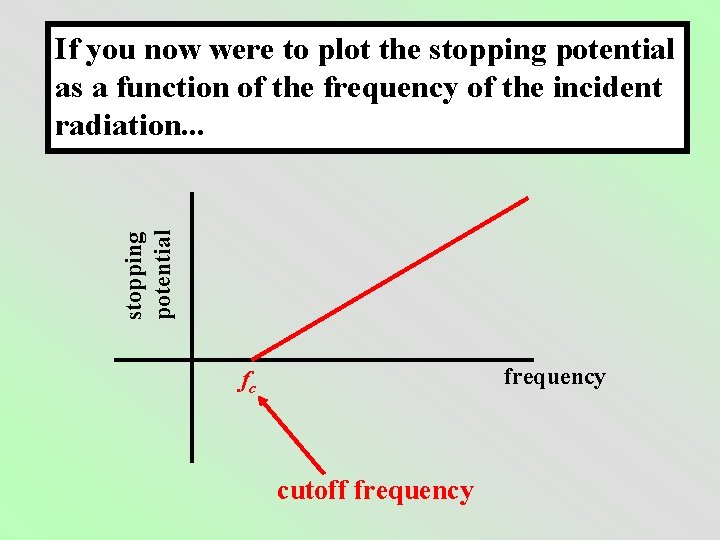
stopping potential If you now were to plot the stopping potential as a function of the frequency of the incident radiation. . . frequency fc cutoff frequency

Recall, the potential energy of a charge in an electric field is simply q. V. In this case, the stopping potential represents the maximum potential difference the electron can cross. So, KEmax = e Vo These observations contradicted the classical theory, which suggested that the current should exist for any frequency of light, so long as the intensity of the light was strong enough. . .

When you fire the ball into the gravel, rocks will fly out. The harder you throw the ball, the faster the rocks fly away.

This analogy illustrates the classical expectation for the interaction of light with the electrons in the metal during the photoelectric experiment. But this model is inconsistent with the observations!

Einstein extended Planck’s concept of energy quantization to electromagnetic waves (light). In particular, Einstein proposed that light actually consisted of a stream of particles known as “photons. ” Being electromagnetic waves, however, each photon has a characteristic wavelength and frequency. The energy of a photon, according to Einstein, is given by E=hf

Einstein also hypothesized the following: Electrons struck by photons incident upon the metal surface must pass through the surface to be freed and conduct electricity across the gap. This barrier is a characteristic of the metal itself and is described as the work function of the metal. As a result, freed electrons will have a maximum kinetic energy given by energy of the incident light Energy required to escape the metal

With this theory, Einstein successfully explained all the observations associated with the photoelectric effect experiment. He received the Nobel Prize in 1921 for this work. Among other things, you have Einstein to thank for our ability to hear the soundtrack at the movie theater! (The edge of movie film contains a strip with varying lights and darks. Light from the projector passes through this strip, illuminating a photo cell. The frequencies of this illumination can be directly translated into audible sound!)

Light is both a wave and a particle! Which you may have already noticed implicitly in our explanation of the photoelectric effect.

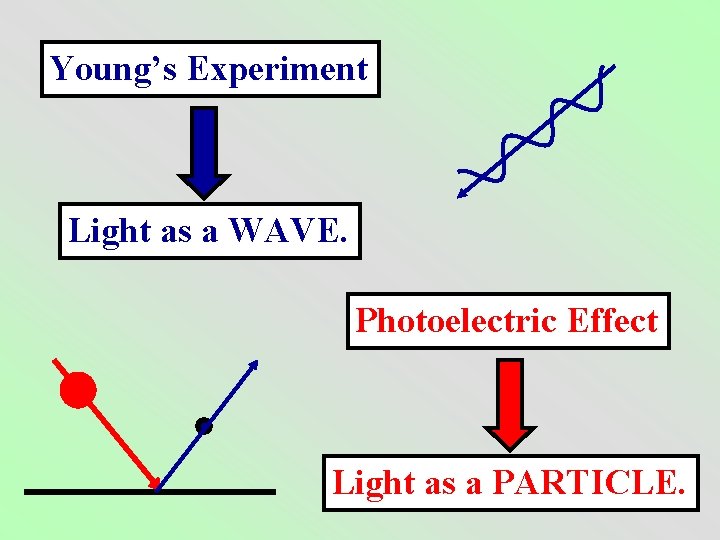
Young’s Experiment Light as a WAVE. Photoelectric Effect Light as a PARTICLE.

Sometimes, light acts like a particle; other times, light acts like a wave. It turns out (and it’s not too hard to convince yourself) that the shorter the wavelength of the light, the more the light acts like a particle and the less it acts like a wave. More similar to a particle High frequency More energy

“Okay, so let’s assume that light is both a particle and a wave. If that’s true, perhaps all matter has both particle and wave characteristics. ” This was exactly the hypothesis of Luis de Broglie in his 1924 dissertation! De Broglie extended Einstein’s theory to cover all matter, not just photons!

According to Einstein, a fundamental relationship exists between energy and momentum: Here, p is the momentum and c the speed of light. (We’ll cover this in more detail when we talk about relativity. )

As we saw in the photoelectric effect, Einstein demonstrated that the energy of a photon of light was related to its frequency: E=hf Combining the two, we find a relationship between the momentum of a photon and its frequency:

Recall that c = f l, so we can express momentum as a function of wavelength: de Broglie’s hypothesis was that any particle with momentum p should also exhibit wave properties with characteristic wavelength l.

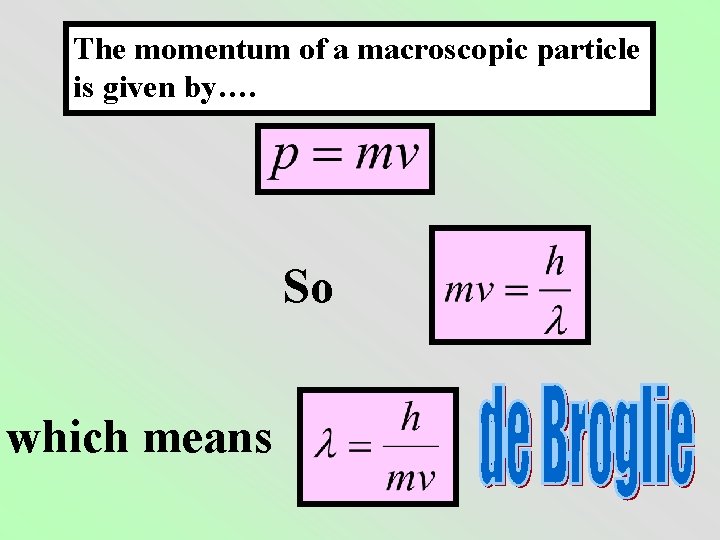
The momentum of a macroscopic particle is given by…. So which means

What is the de Broglie wavelength of a 60 kg person jogging at 5 m/s?

Obviously, we’re never going to observe the diffraction of our jogger! But before we discount de Broglie’s hypothesis entirely, let’s take a look at another example. . .

What is the de Broglie wavelength of an electron moving at 2. 2 X 106 m/s? This is a scale at which diffraction effects may actually be observed. . .

Also notice that the slower the electron travels, the longer the de Broglie wavelength will be! One last great mystery. . .

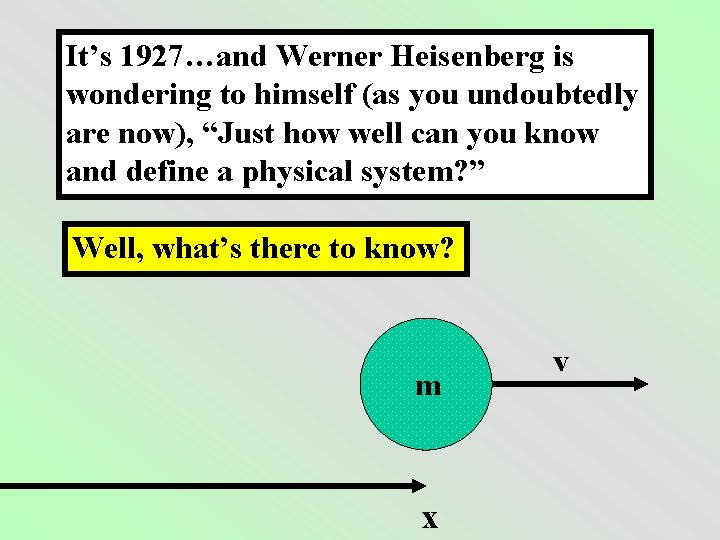
It’s 1927…and Werner Heisenberg is wondering to himself (as you undoubtedly are now), “Just how well can you know and define a physical system? ” Well, what’s there to know? m x v

Mass times velocity is momentum position The two quantities which define a system How well can we know these two quantites? Classically, there are no limits to our measurement precision and accuracy. We can know them both perfectly!

Quantum physics tells us otherwise! Afterall, how is it that we become aware of the characteristics of a physical system? Through observation!

In order to make an observation, LIGHT must be involved! And light can have an impact on matter, changing the momentum and or energy of the system we’re observing! (As we’ve seen in the photoelectric effect and as covered in the text on the Compton effect. )

So by observing the system, we necessarily change the system! The process of observing introduces uncertainties in the physical quantities which characterize the system. If we describe the uncertainty in the momentum of the system as Dp and the uncertainty in the location of the system as Dx, Heisenberg tells us that the uncertainty in these quantities must satisfy the expression. . .

Which says that it is impossible to know both the position and momentum of a particle with infinite accuracy.