Chapter 26 Geometrical Optics Snells Law Thin Lens

Chapter 26 Geometrical Optics Snell’s Law Thin Lens Equation

1) Index of Refraction, n Speed of light is reduced in a medium Air Water Glass Diamond 1. 000293 4/3 1. 5 2. 4

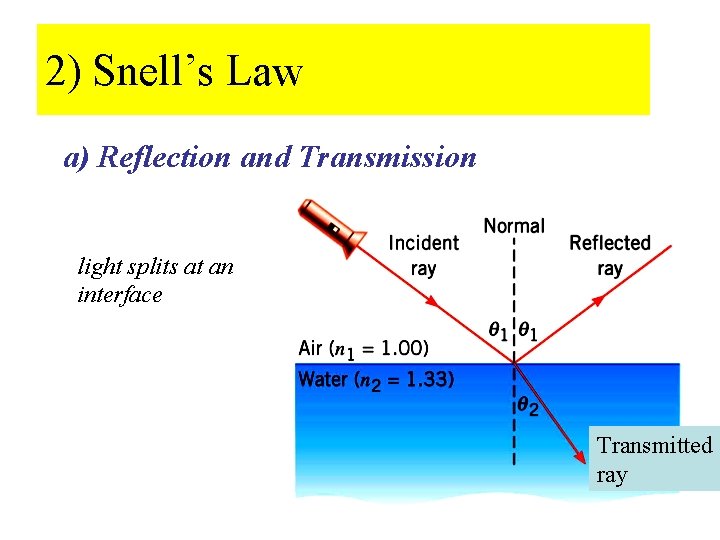
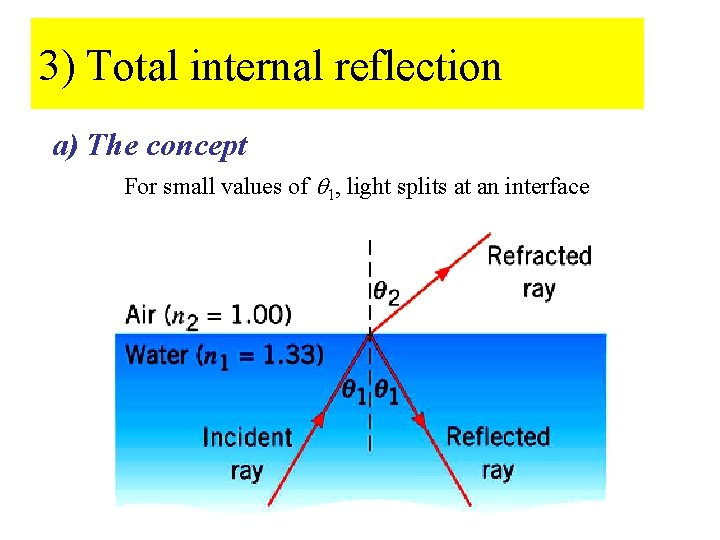
2) Snell’s Law a) Reflection and Transmission light splits at an interface Transmitted ray

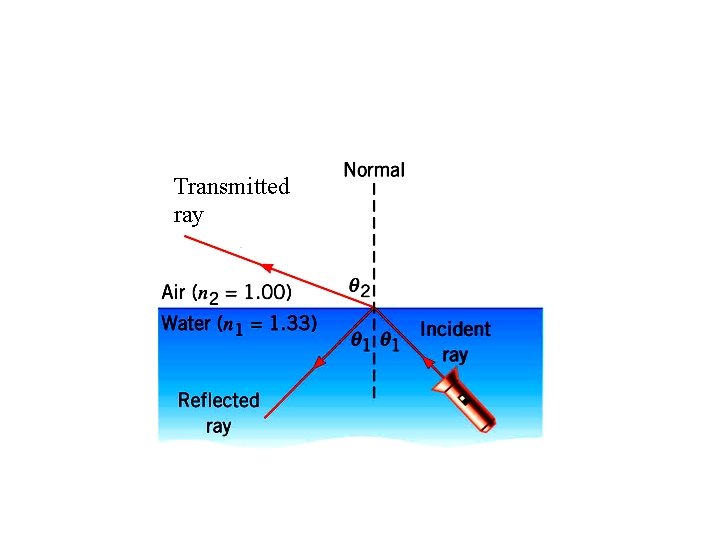
Transmitted ray

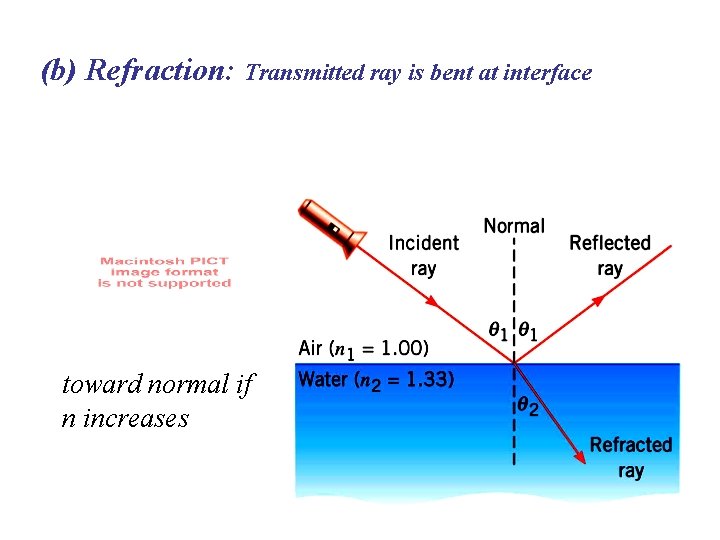
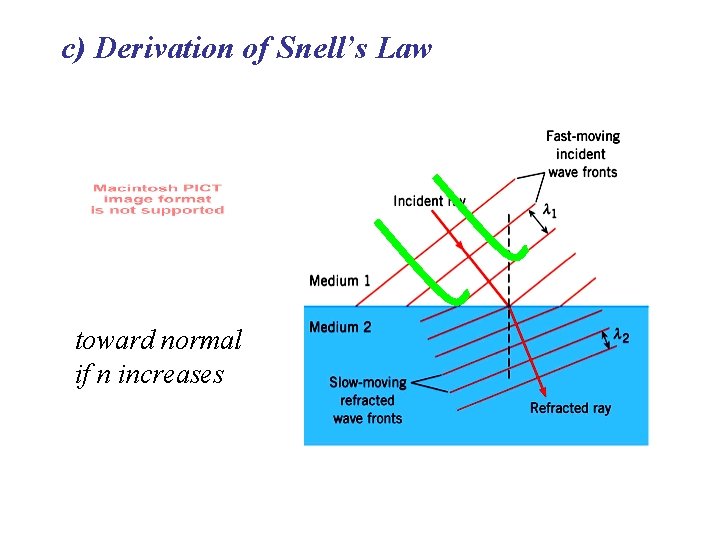
(b) Refraction: Transmitted ray is bent at interface toward normal if n increases

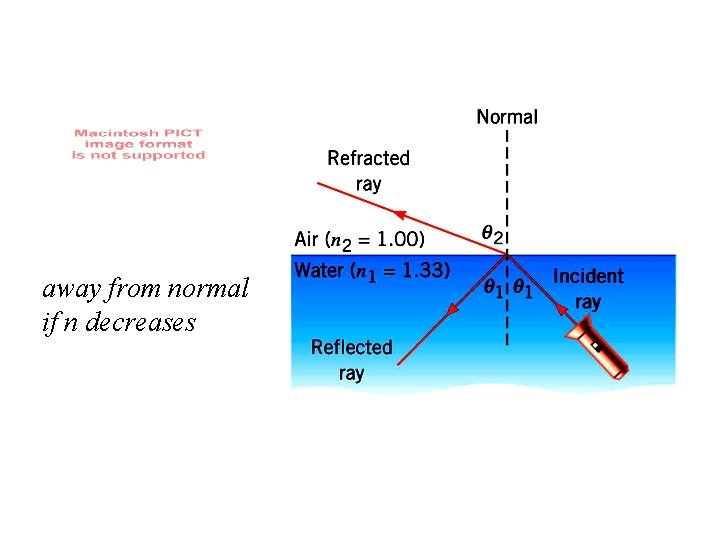
away from normal if n decreases

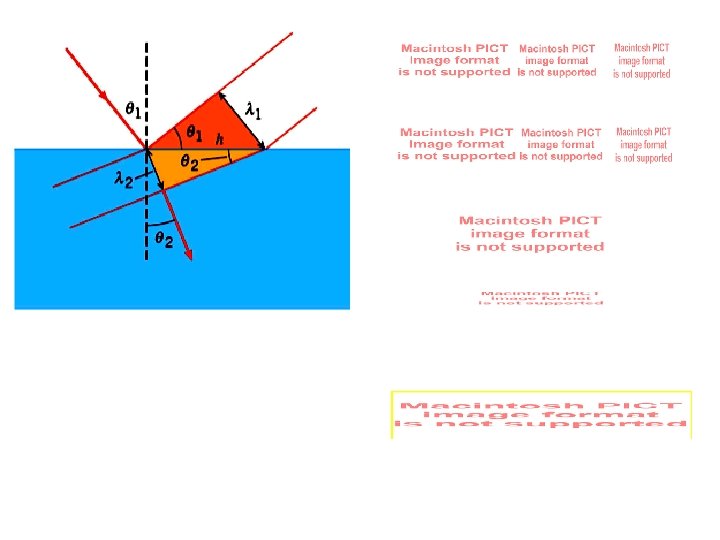
c) Derivation of Snell’s Law toward normal if n increases

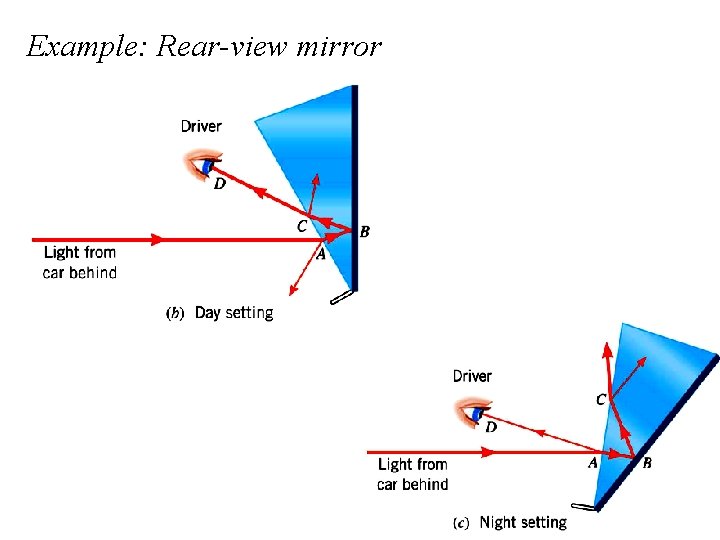
Example: Rear-view mirror

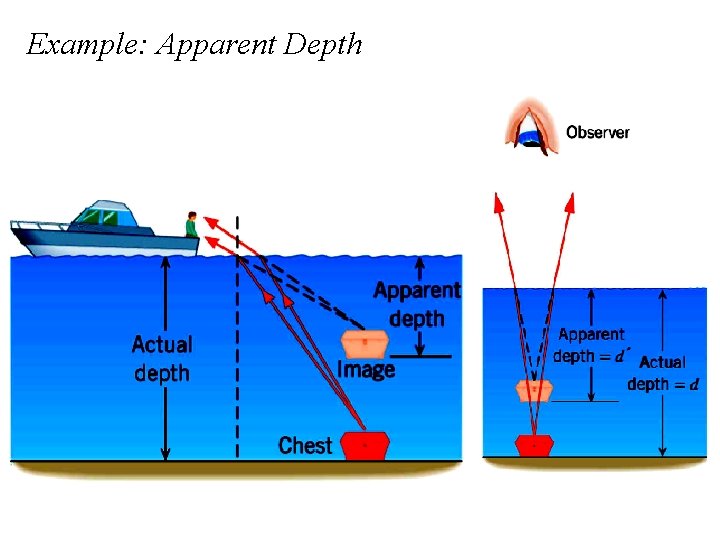
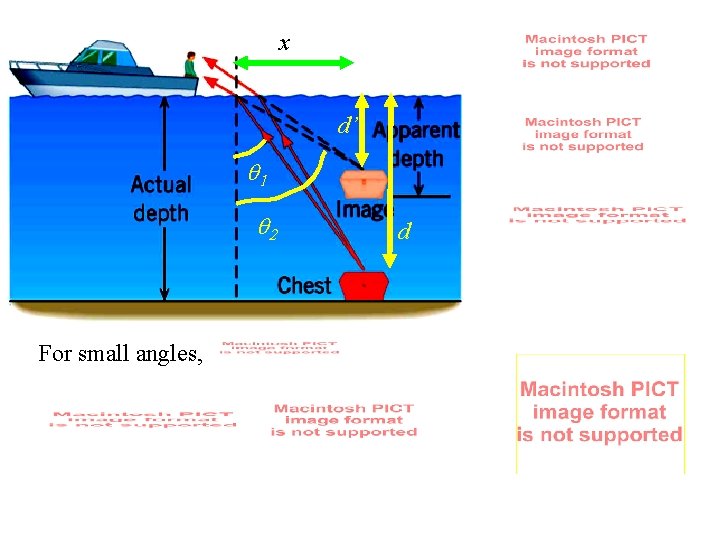
Example: Apparent Depth

x d’ 1 For small angles, d

3) Total internal reflection a) The concept For small values of 1, light splits at an interface

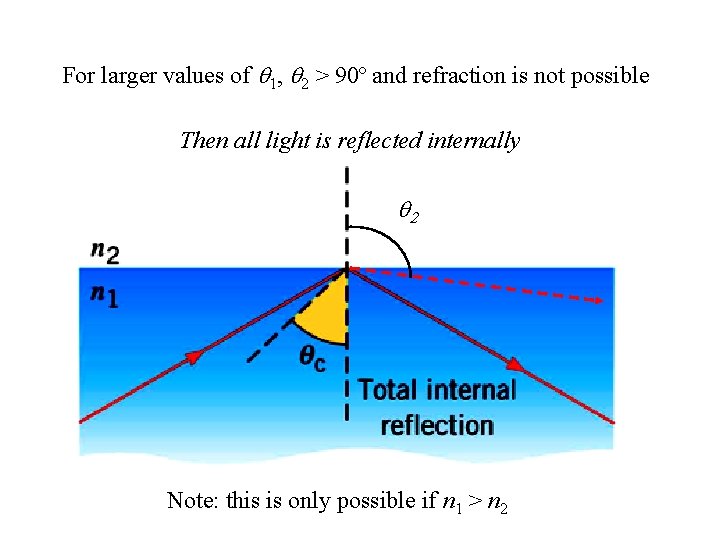
For larger values of 1, 2 > 90º and refraction is not possible Then all light is reflected internally Note: this is only possible if n 1 > n 2

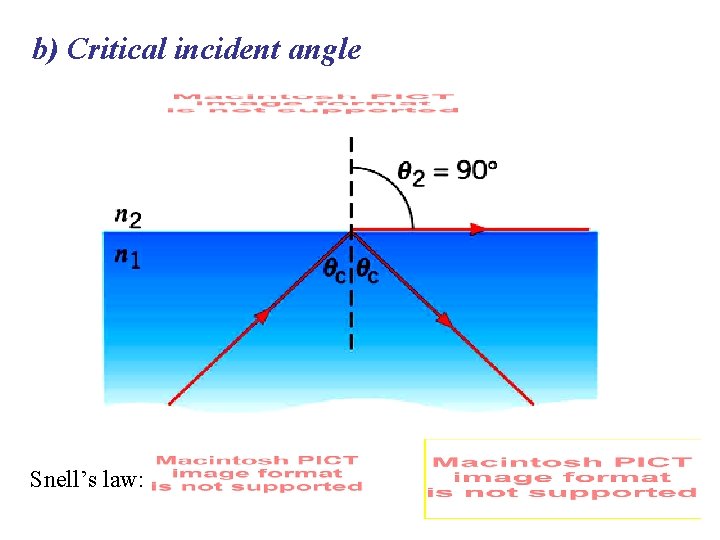
b) Critical incident angle Snell’s law:

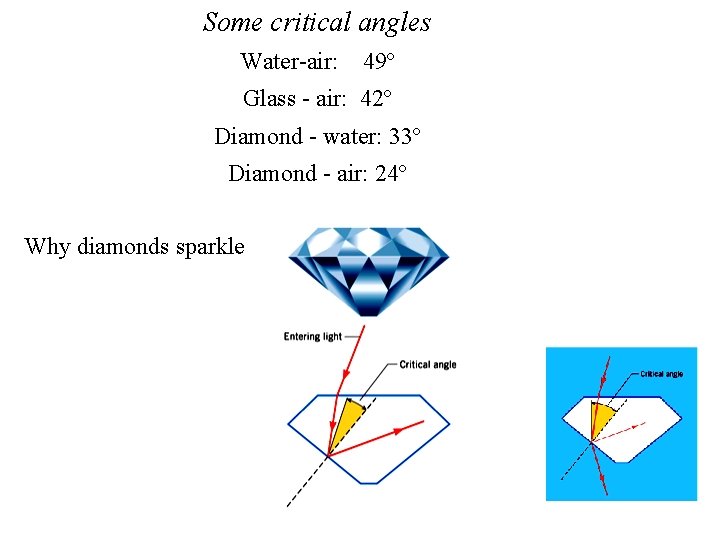
Some critical angles Water-air: 49º Glass - air: 42º Diamond - water: 33º Diamond - air: 24º Why diamonds sparkle

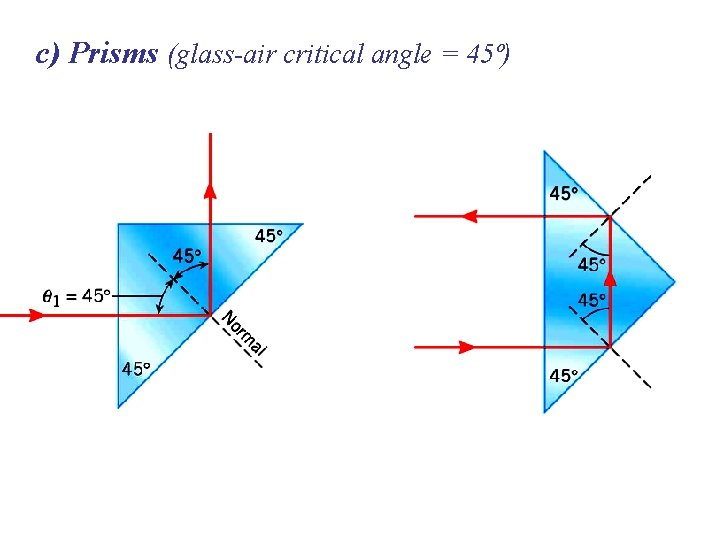
c) Prisms (glass-air critical angle = 45º)

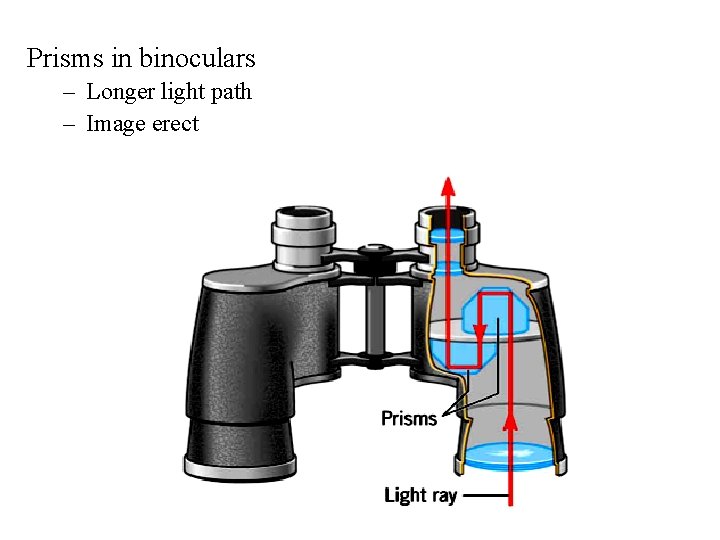
Prisms in binoculars – Longer light path – Image erect

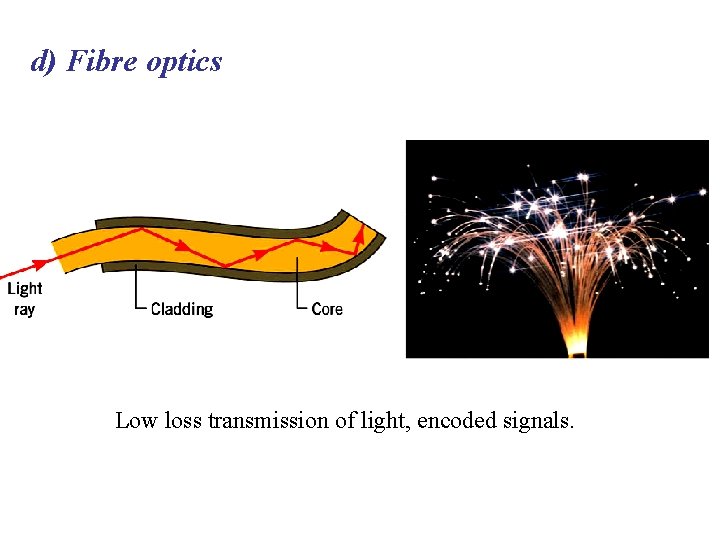
d) Fibre optics Low loss transmission of light, encoded signals.

Fibre optic bundles, coherent bundles Imaging applications: endoscopy

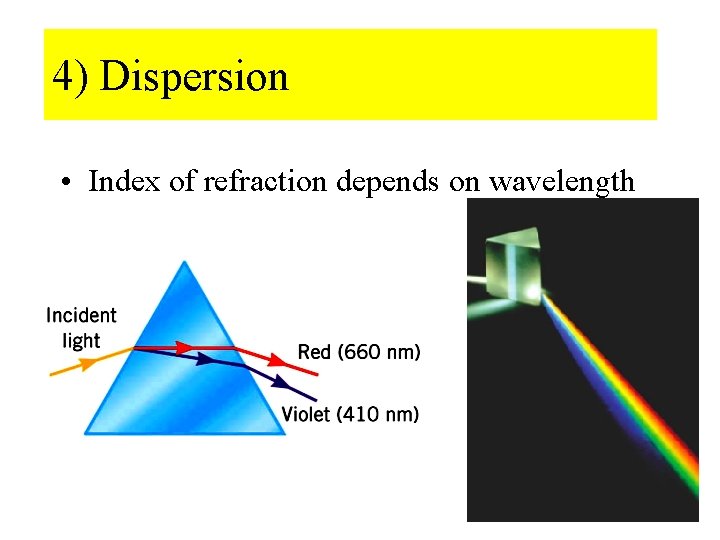
4) Dispersion • Index of refraction depends on wavelength

Rainbow

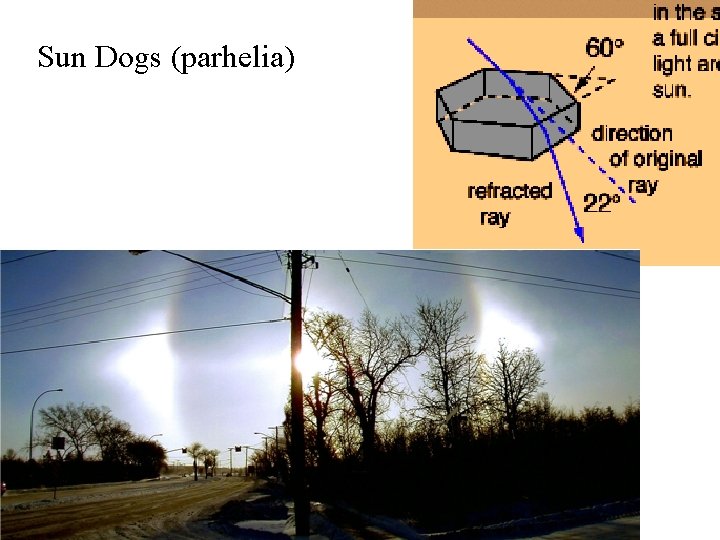
Sun Dogs (parhelia)

5) Image Formation a) Seeing an object Diffuse reflection

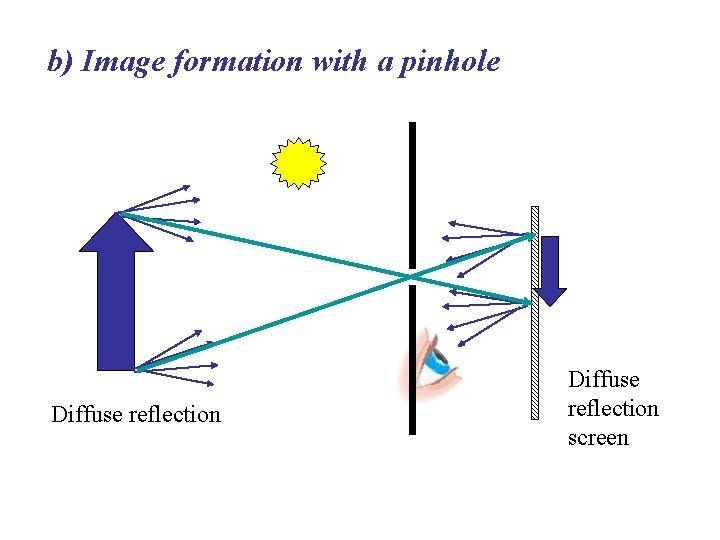
b) Image formation with a pinhole Diffuse reflection screen

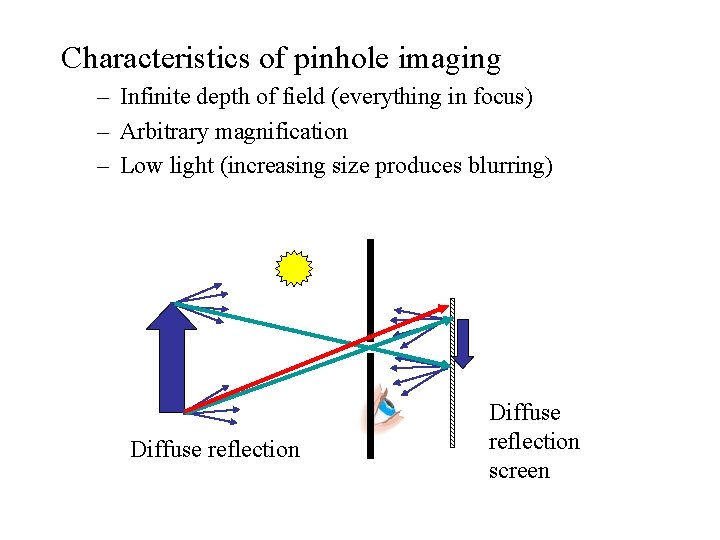
Characteristics of pinhole imaging – Infinite depth of field (everything in focus) – Arbitrary magnification – Low light (increasing size produces blurring) Diffuse reflection screen

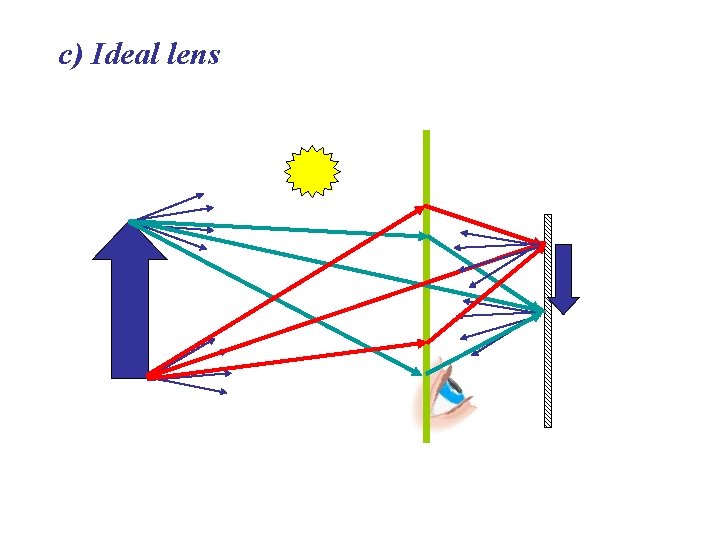
c) Ideal lens

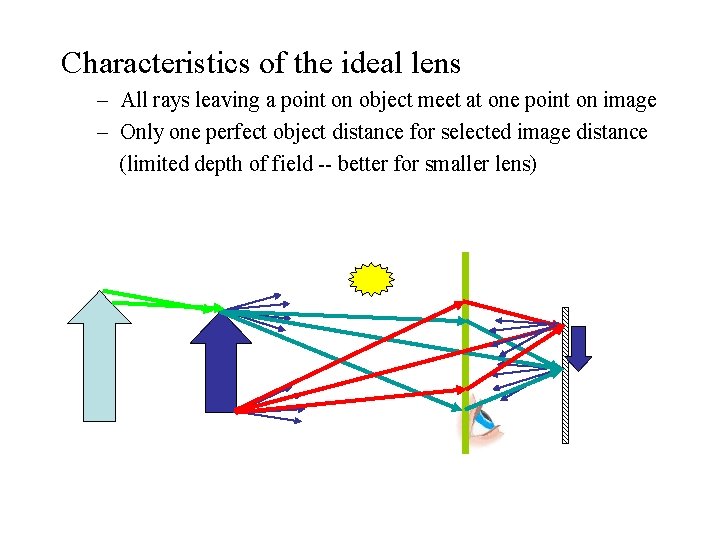
Characteristics of the ideal lens – All rays leaving a point on object meet at one point on image – Only one perfect object distance for selected image distance (limited depth of field -- better for smaller lens)

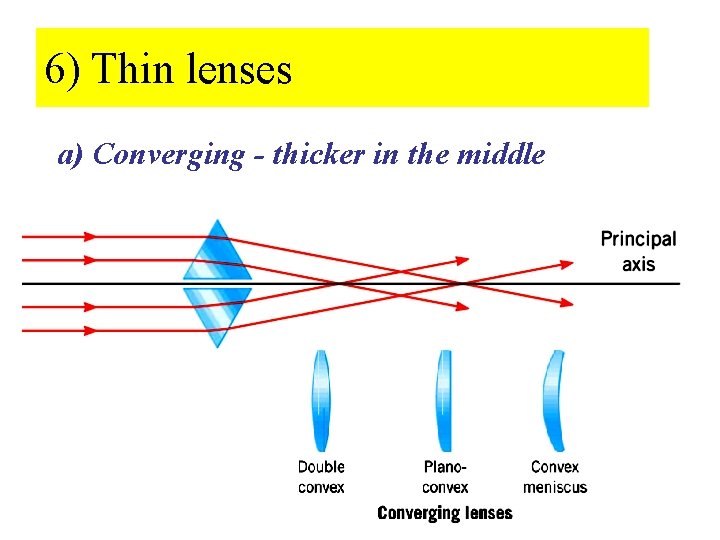
6) Thin lenses a) Converging - thicker in the middle

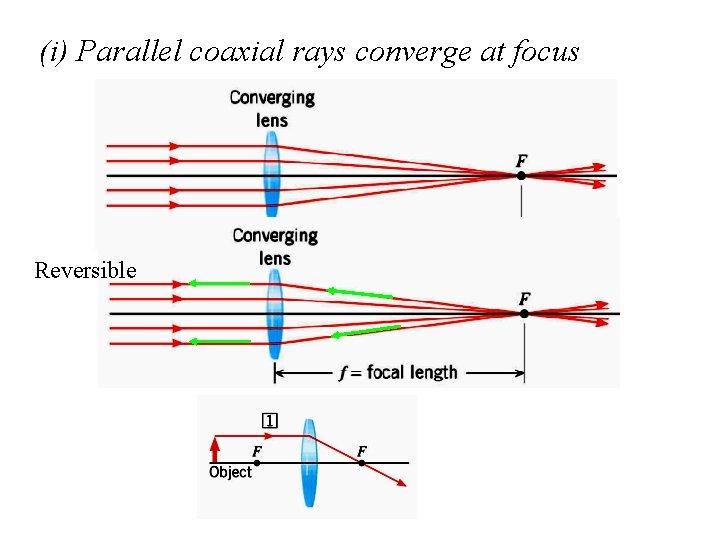
(i) Parallel coaxial rays converge at focus Reversible

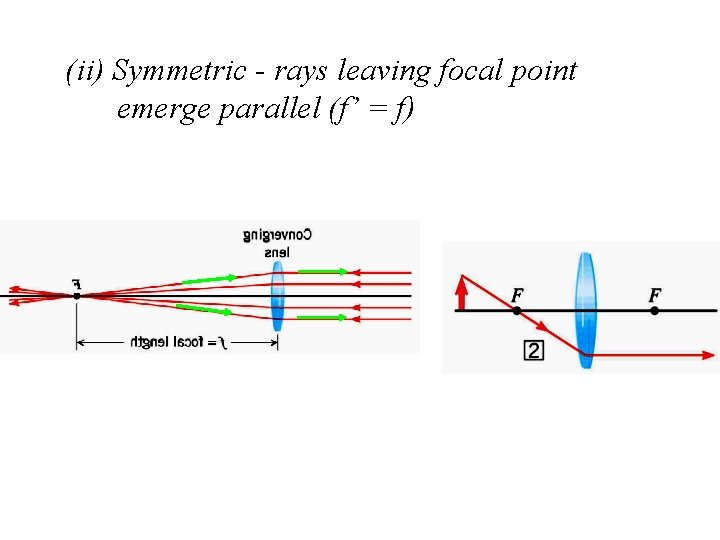
(ii) Symmetric - rays leaving focal point emerge parallel (f’ = f)

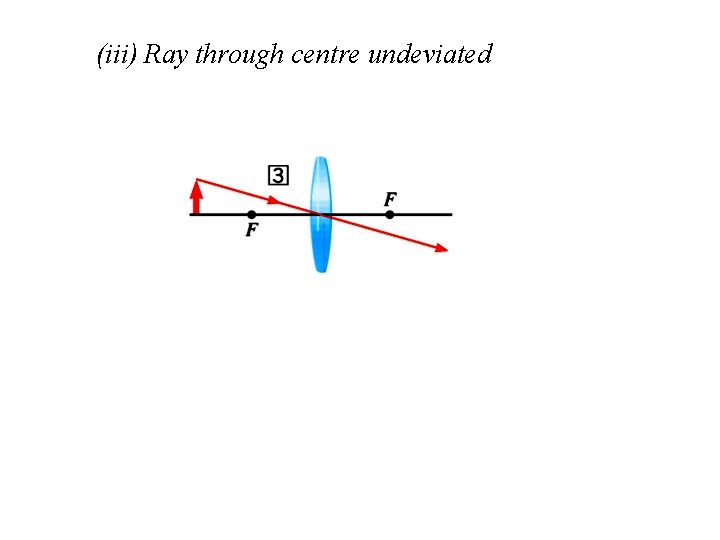
(iii) Ray through centre undeviated

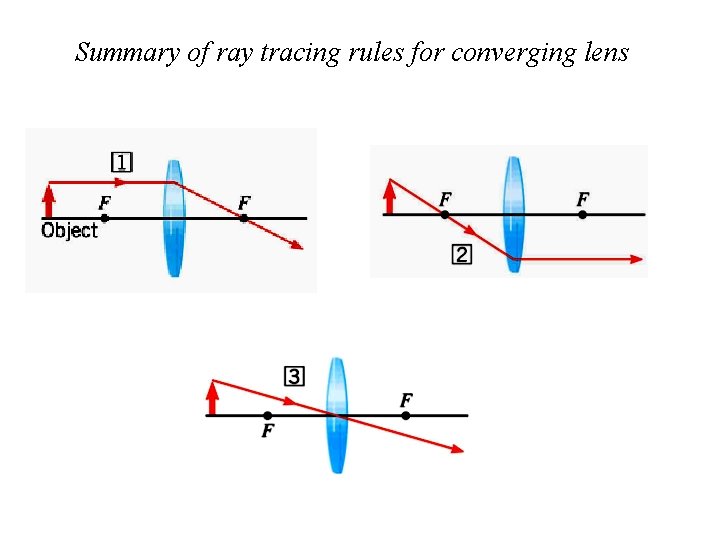
Summary of ray tracing rules for converging lens

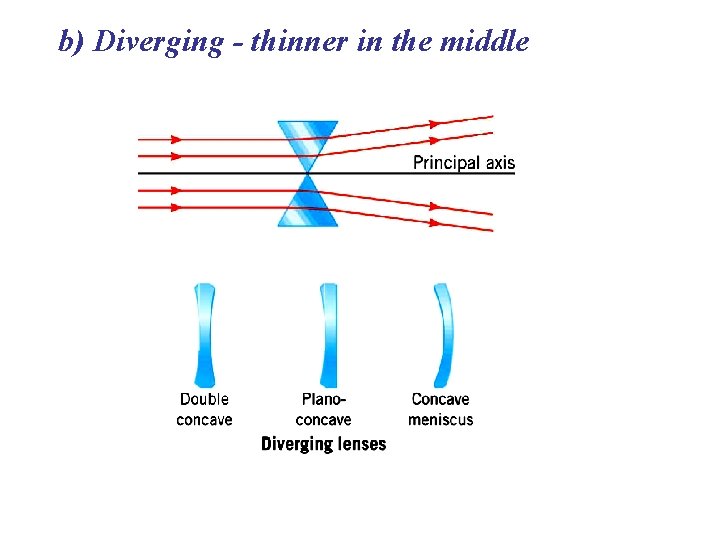
b) Diverging - thinner in the middle

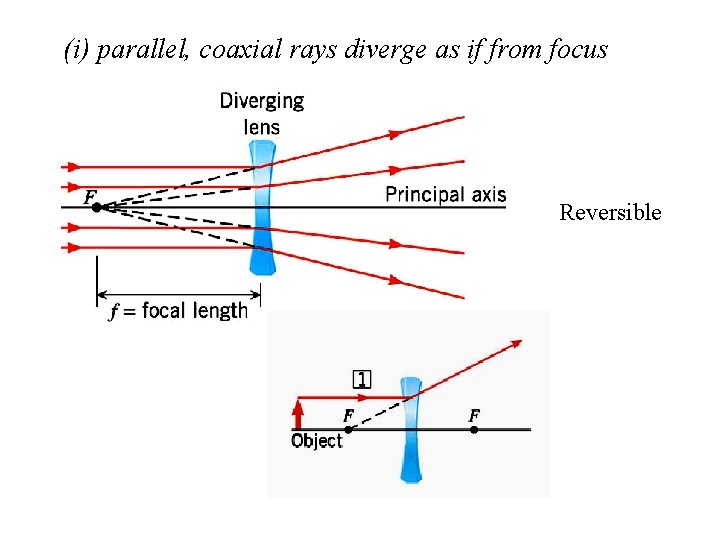
(i) parallel, coaxial rays diverge as if from focus Reversible

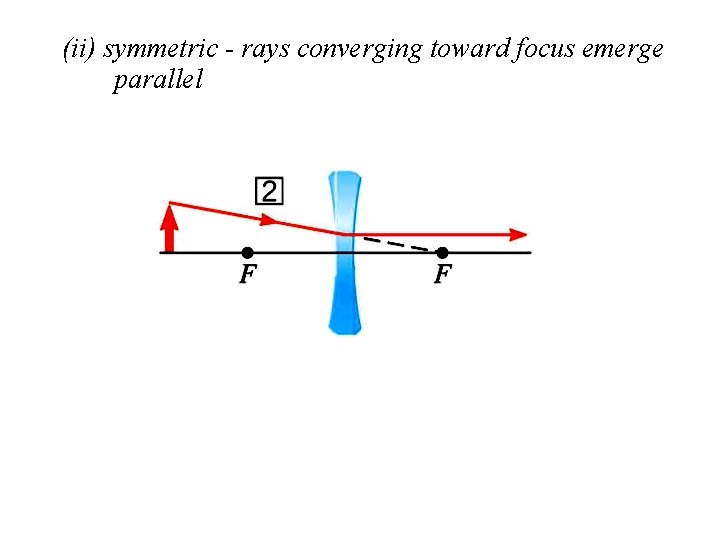
(ii) symmetric - rays converging toward focus emerge parallel

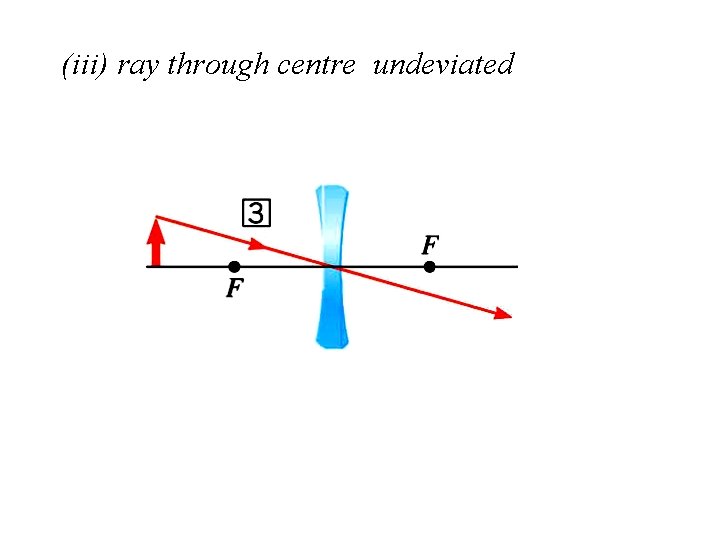
(iii) ray through centre undeviated

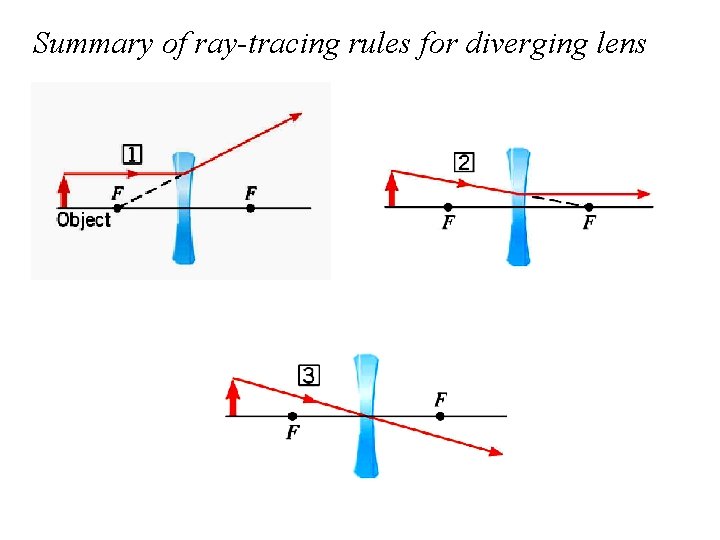
Summary of ray-tracing rules for diverging lens

c) Real lenses: - usually spherical surfaces - approximate ideal lens for small angles (paraxial approximation)

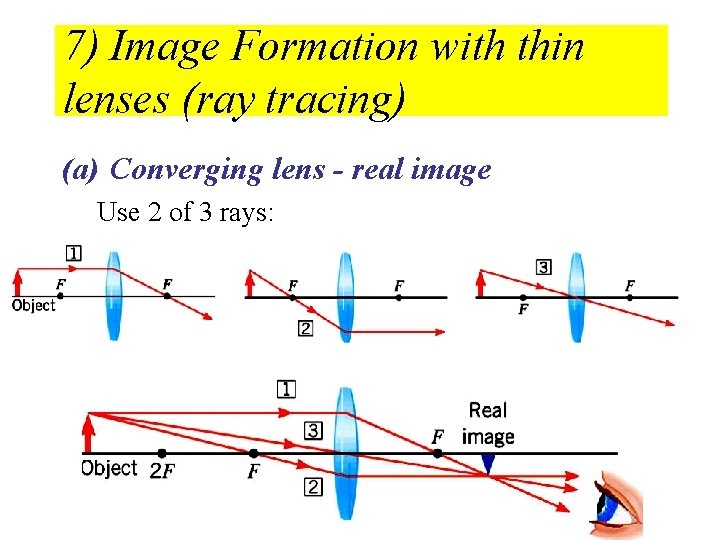
7) Image Formation with thin lenses (ray tracing) (a) Converging lens - real image Use 2 of 3 rays:

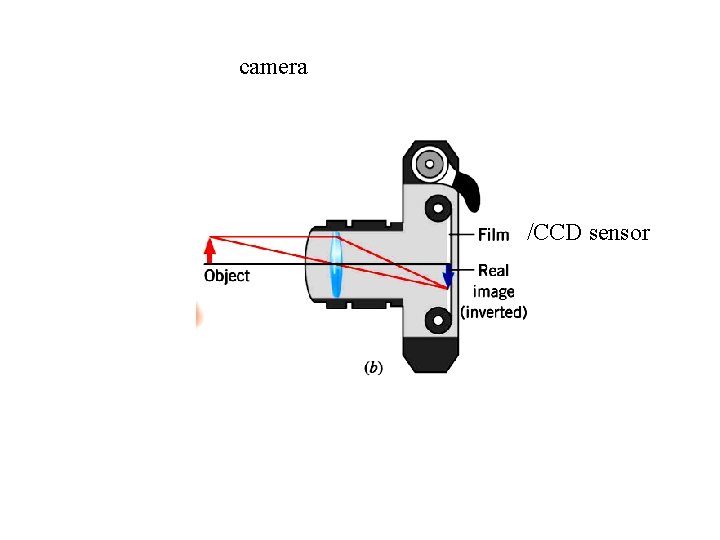
camera /CCD sensor

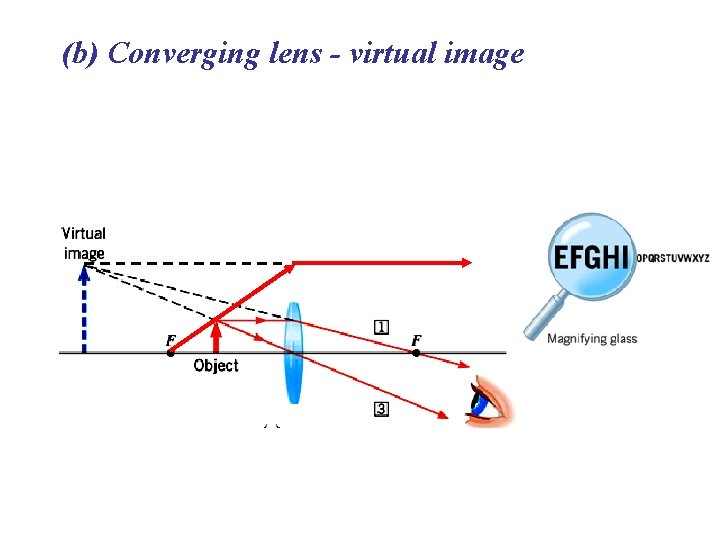
(b) Converging lens - virtual image

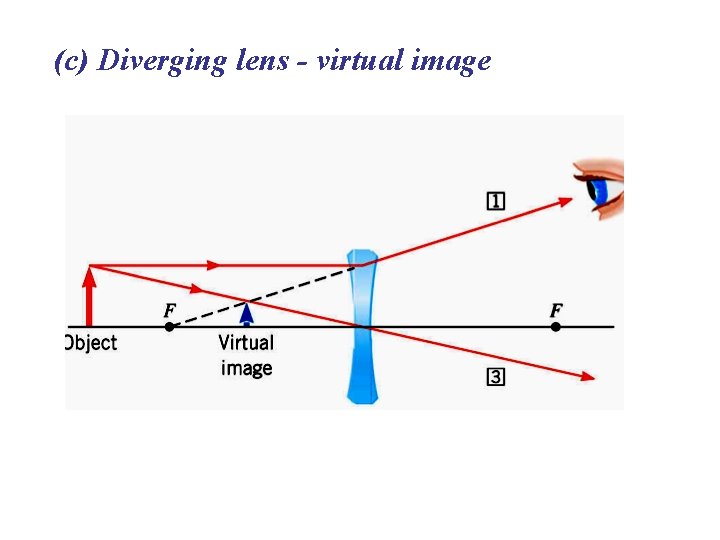
(c) Diverging lens - virtual image

8) Thin Lens Equation a) The equation

b) Sign Convention (left to right) (i) Focal Length: f > 0 converging f < 0 diverging (ii) Object distance do > 0 left of lens (real; same side as incident light) do < 0 right of lens (virtual; opposite incident light) (iii) Image distance di > 0 right of lens (real; opposite incident light) di < 0 left of lens (virtual; same side as incident light) (iv) Image size hi > 0 erect hi < 0 inverted

c) Lateral magnification Definition: From geometry (and sign convention):

9) Compound Lenses Image of first lens is object for the second lens. Apply thin lens equation in sequentially.

Overall magnification is the product:

Example: Problem 26. 66 Find final image and magnification.

10) Vision and corrective lenses a) Anatomy of the eye

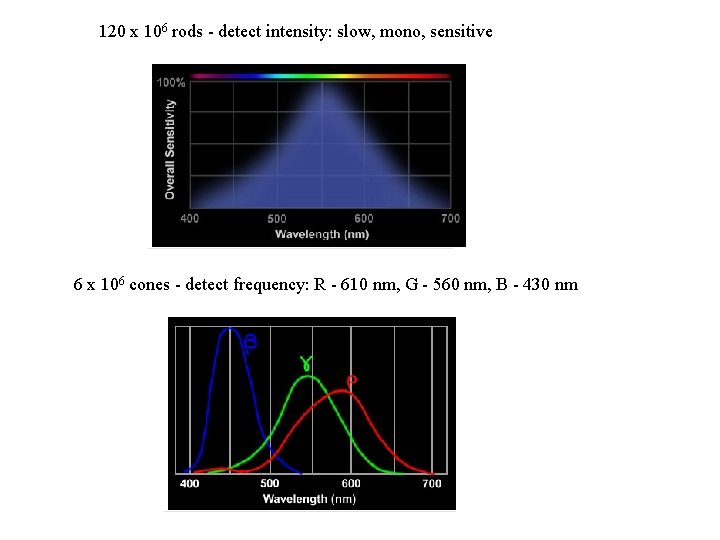
120 x 106 rods - detect intensity: slow, mono, sensitive 6 x 106 cones - detect frequency: R - 610 nm, G - 560 nm, B - 430 nm

b) Optics - Accomodation: focal length changes with object distance - near point: nearest point that can be accomodated - normally < 25 cm - far point: furthest point that can be accomodated - normally ∞

c) Myopia - far point < ∞ - near-sighted (far-blind) - correction: object at ∞ --> image at far point

Correction: object at ∞ --> image at far point (ignoring the eye-lens distance)

d) Refractive Power For a far point of 50 cm, f = -50 cm, Lens prescription: -2

e) hyperopia (hypermetropia) - near point > 25 cm - far-sighted (near-blind) - correction: object at 25 cm --> image at near point

Correction: object at 25 cm --> image at near point (ignoring the eye-lens distance) For near point of 40 cm, f = 66 cm Power = + 1. 5 (reading glasses)

Examples: Problem 26. 73 Age 40: f = 65. 0 cm --> NP’ = 25. 0 cm Age 45: NP’ --> 29. 0 cm (a) How much has NP (without glasses) changed? (b) What new f is needed? Problem 26. 75 FP = 6. 0 m corrected by contact lenses. (Find f) An object (h = 2. 0 m) is d = 18. 0 m away. • Find image distance with lenses. • Find image height with lenses.

11) Angular Magnification a) Angular size

b) Angular magnification

12) Magnifier With magnifier: (Magnifier allows object to be close to the eye)

Without magnifier: Highest magnification (di = -N): (tense eye) Lowest magnification (di = -∞): (relaxed eye) (Magnification quoted with N = 25 cm, for relaxed eye)

Example: Problem 26. 82 Farsighted person has corrective lenses with f = 45. 4 cm. Maximum magnification of a magnifier is 7. 50 (normal vision). What is the maximum magnification of the magnifier for the farsighted person without lenses?

13) Compound Microscope • Simple magnifier: M = N/f – to increase M, decrease f – practical limits to decreasing f (and therefore size): • small lens difficult to manufacture and use • increases aberrations • Microscope introduces an additional lens to form a larger intermediate image, which can be viewed with a magnifier

Magnification: For image at ∞, di 2 = fe L For max M, do 1 fo For di 2 = ∞, di 1 + fe = L

Example: Problem 26. 88 Microscope with fo = 3. 50 cm, fe = 6. 50 cm, and L = 26. 0 cm. (a) Find M for N = 35. 0 cm. (b) Find do 1 (if first image at Fe) (c) Find lateral magnification of the objective.

14) The Astronomical Telescope • Magnifier requires do < f, but do -> ∞ for stars • Introduce objective to form nearby image, then use magnifier on the image

Magnification: Long telescope, small eyepiece

Example: Problem 26. 94 Yerkes Observatory: fo = 19. 4 m, fe = 10. 0 cm. (a) Find angular magnification. (b) If ho = 1500 m (crater), find hi, given do = 3. 77 x 108 m (c) How close does the crater appear to be.

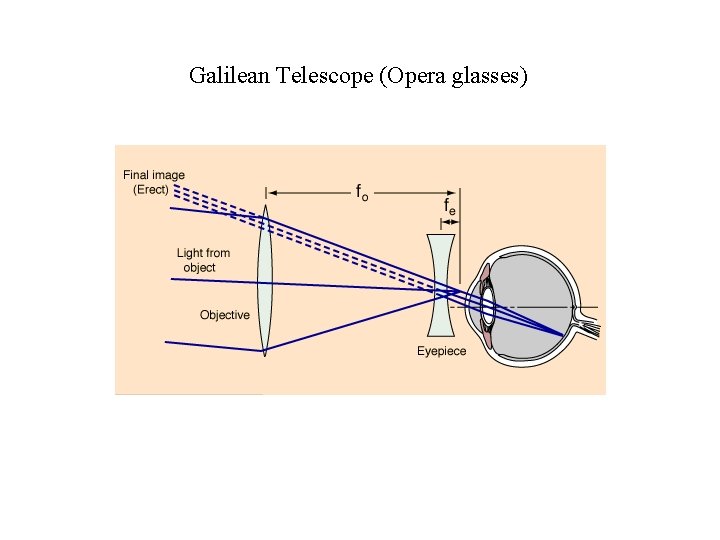
Galilean Telescope (Opera glasses)

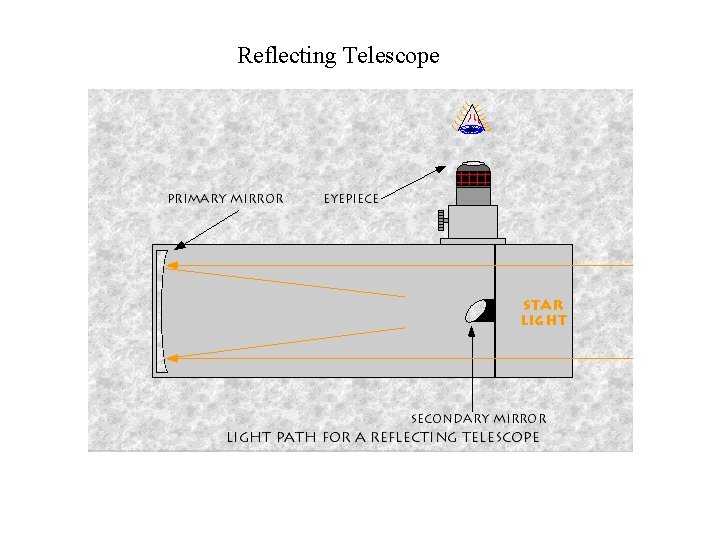
Reflecting Telescope